기계학습을 이용한 수학 연구 (사례연구: 머머레이션)

여는 말

인공지능이 세상을 변화시키는 것이 분명한데 수학도 바꿀까요? 현재 수학에서 가장 중요하다는 리만가설을 인공지능이 수천 페이지에 걸쳐 증명했다는 뉴스가 머지않아 나올까요? 그런 날이 언젠가는 올 수도 있겠지만, 수학 연구가 직업인 저로서는 다행스럽게도, 아직은 인공지능이 수학자를 대체하기는 어려워 보입니다. 현재로서는 그보다는 오히려 수학자들이 인공지능, 특히 기계학습을 이용해서 기존의 연구 방법과는 사뭇 다른 접근 방법을 적용함으로써 새로운 결과를 창출해 낼 수 있는 황금 같은 기회가 생겼다고 저는 믿습니다.

제 의견에 동의를 구하기 위해, 이 글에서 제가 최근에 경험한 한 가지 예를 소개하려고 합니다. 한 가지 예이기는 하지만, 수학 연구에 기계학습을 어떻게 이용할 수 있는지에 대한 패러다임을 제시한다고 생각합니다. 이 패러다임은 “수학은 데이터과학이다”라고 여기고 출발해서 다음과 같은 네 단계를 거칩니다. 첫째로, 개별적인 수학적 객체를 하나씩 하나씩 연구하는 대신 객체들을 한꺼번에 많이 모아서 집합을 만들고 관심 있는 성질을 살펴서 데이터를 생성합니다. 둘째로, 여러 가지 기계학습 도구들을 적용하고 그 결과들을 분석합니다. 셋째로, 기계학습이 찾아낸 패턴과 법칙을 수학적으로 해석해서 새로운 추측을 만듭니다. 마지막으로, 엄밀한 수학적 방법론을 이용해서 추측을 증명함으로써 새로운 정리를 얻습니다.

이러한 패러다임을 적용하는 연구 분야를 “수학적 데이터과학^{mathematical data-science}” 혹은 관점을 달리해 “데이터과학적 수학^{data-scientific mathematics}”라고 부를 수 있겠습니다.

참새 무리와 타원곡선 모임의 닮은 점

제가 지금부터 한 가지 예로 소개하려는 기계학습을 이용한 수학 연구는 그 결과로 타원곡선의 머머레이션^murmuration이라는 새로운 현상을 발견하였습니다. 원래 머머레이션은 참새의 일종인 찌르레기가 큰 무리를 지으면서 만들어 내는 군집현상을 말합니다.

타원곡선
      
이제 본격적으로 수학 얘기를 하기 위해 타원곡선에 대해 몇 가지 정의를 하겠습니다. 유리수체 $\mathbb{Q}$ 위의 타원 곡선은 다음과 같은 삼차 방정식으로 주어집니다.$$y^2 = x^3 + a x + b.$$여기서 $a, b$는 정수 계수입니다. 이 방정식을 만족하는 $(x, y) \in \mathbb{Q} \times \mathbb{Q}$ 쌍을 유리점(rational point)이라고 합니다. 예를 들어, $$y^2 = x^3 + x + 1$$은 하나의 타원 곡선이고, 쉽게 볼 수 있듯이 $(0,1)$이 유리점입니다. 이 곡선 위에 유리점이 몇 개나 있을까요? 무한히 많습니다. 몇 개 적어 보면 다음과 같습니다.

$$\left(\frac{1}{4} , \frac{9}{8} \right), \left(-\frac{287}{1296} , \frac{40879}{46656} \right), \left(\frac{43992}{82369} , \frac{30699397}{23639903} \right), \left(\frac{26862913}{1493284} , \frac{139455877527}{1824793048} \right)$$
복잡하지만 사실 $(0,1)$로 부터 다 만들어 낼 수 있습니다. 이 경우를 차수^rank가 1이라고 합니다. 반면에 비슷해 보이지만 타원곡선 $$y^2 = x^3+1$$위에는 유리점이 다섯 개밖에 없습니다. (다 찾으실 수 있을까요?) 보통 사영기하 입장에서 타원곡선을 보기 때문에 무한원점을 포함시켜서 유리점이 여섯 개라고 말합니다. 이처럼 유리점이 유한 개인 경우를 차수가 0이라고 하겠습니다. 유리점이 무한히 많은 경우에 차수가 2 이상인 경우가 있는데, 모든 유리점을 만들어 내기 위해 두 개 이상의 유리점이 필요한 경우입니다.

타원 곡선은 오랜 세월 동안 연구되어 왔지만, 차수에 대해서는 여전히 많은 미해결 난제들이 존재합니다. 특히, 타원 곡선에 대한 BSD 추측^{Birch and Swinnerton-Dyer conjecture}이 직접적으로 차수에 대한 예측이고 리만가설 등과 함께 문제당 백만 달러 상금이 걸린 여섯 개의 미해결 문제 중 하나입니다. 이렇게 중요하고 어려운 문제에 한 발이라도 더 접근하기 위해 뭐라도 할 수 있으면 좋을텐데, 혹시 기계학습이 도움이 될까요? 저도 궁금해서 몇 년 전에 동료 수학자들인 허양희^{Yang-Hui He}, 토마스 올리버 ^{Thomas Oliver}, 알렉세이 파즈드냐코프^{Alexey Pozdnyakov}와 함께 기계학습을 이용해서 타원 곡선을 차수에 따라 분류할 수 있는지 실험을 했습니다[1].

기계학습 실험      

우선 기계에 타원곡선들을 보여 주어야 할텐데 어떻게 하면 ‘좋은 사진’을 찍어서 보여 줄 수 있을까 고민해 보다 $L$-함수의 계수를 이용할 수 있을 것이라는 생각을 했습니다. $L$-함수는 산술적으로 중요한 대상에 대해 각 소수 $p$ 마다 핵심적인 정보를 가진 $a_p$ 값을 계산해서 정의됩니다. 우리의 경우, 타원곡선 $E$가 있으면 $a(E)=(a_2, a_3, a_5, a_7, \dots)$로 주어진 무한수열이 정해지고 이를 이용해서 그 타원곡선의 $L$-함수가 정의됩니다. 여기서 $a(E)$의 앞부분을 취해서 길이가 적당한 유한수열을 얻고, 그 수열을 타원곡선 $E$의 사진으로 사용하는겁니다. 수열이 어떻게 사진이 되는가 하실지 모르지만, 기계는 어차피 사진을 숫자들의 모임으로 받아들이기 때문에, 수열을 사진으로 생각하는 것은 자연스럽습니다.

주어진 타원곡선 $E$와 소수 $p$에 대해 $a_p$ 값을 얻는 방법은 정수들을 $p$로 나눈 나머지들로만 생각해서 $E$ 위에 ‘나머지 정수점’들이 몇 개나 있는지 세서 그 개수를 $n_p$라 하고 다음과 같이 정의하는 것입니다. $$a_p := p+1 – n_p$$ 
예를 들어, $E$가 $y^2=x^2+x+1$으로 주어진 경우에 소수 $5$를 생각하면, 나머지들이 $\{ 0 , 1, 2, 3, 4 \}$이고 가능한 $(x,y)$ 쌍은 $25$개입니다. 이 $25$개의 쌍을 방정식에 하나씩 다 넣어볼 수 있습니다. 우선 $(1,2)$를 $y^2 = x^2 + x + 1$에 넣어보면 $4 = 3$ 이 되어 양변이 $5$로 나눈 나머지가 다르므로 $(1,2)$는 나머지 정수점이 아니고, 다음으로 $(4,1)$을 넣어보면 $1 = 21$ 이 되어 양변이 $5$로 나눈 나머지가 같아서 $(4,1)$은 나머지 정수점이 됩니다. 이런식으로 모든 쌍을 조사해보면 여덟개의 쌍이 방정식을 만족해서 무한원점까지 합쳐서 $n_5=9$입니다. 따라서 $a_5=5+1-9=-3$이 됩니다. 이런 식으로 계산해서 얻은 길이가 20인 $E$의 수열, 즉 무한수열 $a(E)$의 앞 $20$개 항으로 이루어진 수열은 다음과 같습니다.

$$(a_2, a_3, a_5, \dots , a_{71})=(0, 0, -3, 3, -2, -4, 0, -1, -4, -6, -1, -10, 7, 10, -12, -4, -3, 12, 12, 13)$$
좀 더 계산해서 길이가 300 정도 되면 꽤나 해상도 좋은 $E$의 그림으로 사용할 수 있겠습니다.

한 가지 더 중요하게 고려할 점은 타원곡선들이 복잡한 정도가 천차만별이라는 것입니다. 복잡도를 정하는 방법은 여러 가지가 있는데 컨덕터^conductor라는 값을 이용할 수 있습니다. 위에서 생각한 $y^2=x^3+x+1$로 주어진 타원곡선은 컨덕터가 496입니다. 반면 $y^2=x^3+349x-2018$로 주어진 타원곡선은 컨덕터가 1,093,699입니다. 복잡한 정도가 현저히 다른 타원곡선들을 섞어서 생각하는 것은 사진 찍을 때 해상도 문제도 있고 좋은 생각이 아닌 것 같습니다. 그래서 복잡도가 너무 심하게 차이 나지 않는 타원곡선들을 묶어서 생각하기로 했습니다.

지금껏까지 해온 생각을 적용해서 컨덕터가 1부터 10,000 사이에 있는 타원곡선들 중에 차수 0인 타원곡선 16,000개와 차수 1인 타원곡선 16,000개를 모으고 각 곡선에 대해 길이가 300인 수열을 계산해서 데이터셋을 만들었습니다. 생물학에서 기계학습을 적용하기 위해 해상도 300인 타입 0 세포 사진 16,000장과 타입 1 세포 사진 16,000장을 모은 것과 비슷한 상황입니다. 데이터셋이 준비 되었으니 여러가지 기계학습 도구들을 적용할 수 있었습니다.

결과는 예상을 뛰어넘어, 아주 정말로, 인상적이었습니다. 표준적인 기법인 로지스틱 회귀^{logistic regression}를 이용해서 기계학습 모델을 생각한 후, 데이터셋의 70%를 모델을 학습시키는데 사용하고 나머지 30%를 모델의 학습정도를 검증하기 위해 분리해 놓았습니다. 학습이 끝난 후, 기계에게 검증을 위해 준비한 타원곡선들을 하나씩 보여 주면서 차수가 0인지 1인지 판별하게 했더니, 놀랍게도 정확도 99%를 보였습니다! “아니 어떻게 이럴수가”라는 생각이 들었습니다. 도대체 기계가 뭘 보고 있는지 궁금해졌습니다. 기계에게 타원곡선 이론을 알려 준 일이 없고 차수를 설명해 주지도 않았는데 어떻게 차수 0과 차수 1을 이렇게까지 정확하게 구별하는지 알고 싶어졌습니다.

주성분 분석      

기계학습 결과를 이해하기 위해 실험에 쓰인 타원곡선 데이터셋을 좀 더 자세히 살펴보기로 했습니다. 이를 위해 데이터과학에서 이용하는 가장 기본적인 방법 중 하나인 주성분 분석^{principal component analysis}을 수행했습니다. 데이터셋의 한 원소, 즉 타원곡선 하나의 길이가 300인 수열은 좌표가 300개인 점에 해당한다고 이해할 수 있고, 우리의 데이터셋은 300 차원 공간에 흩어져 있는 점들의 구름으로 볼 수 있습니다. 그 구름이 가장 넓게 펼쳐져 있는 방향을 찾아서 첫 번째 축으로 삼고 그 다음으로 넓게 펼쳐진 방향을 찾아서 두 번째 축으로 삼은 후, 그 두 방향이 만드는 평면 위로 데이터 구름을 투영시켜서 그 이미지를 보는 것이 아이디어입니다.

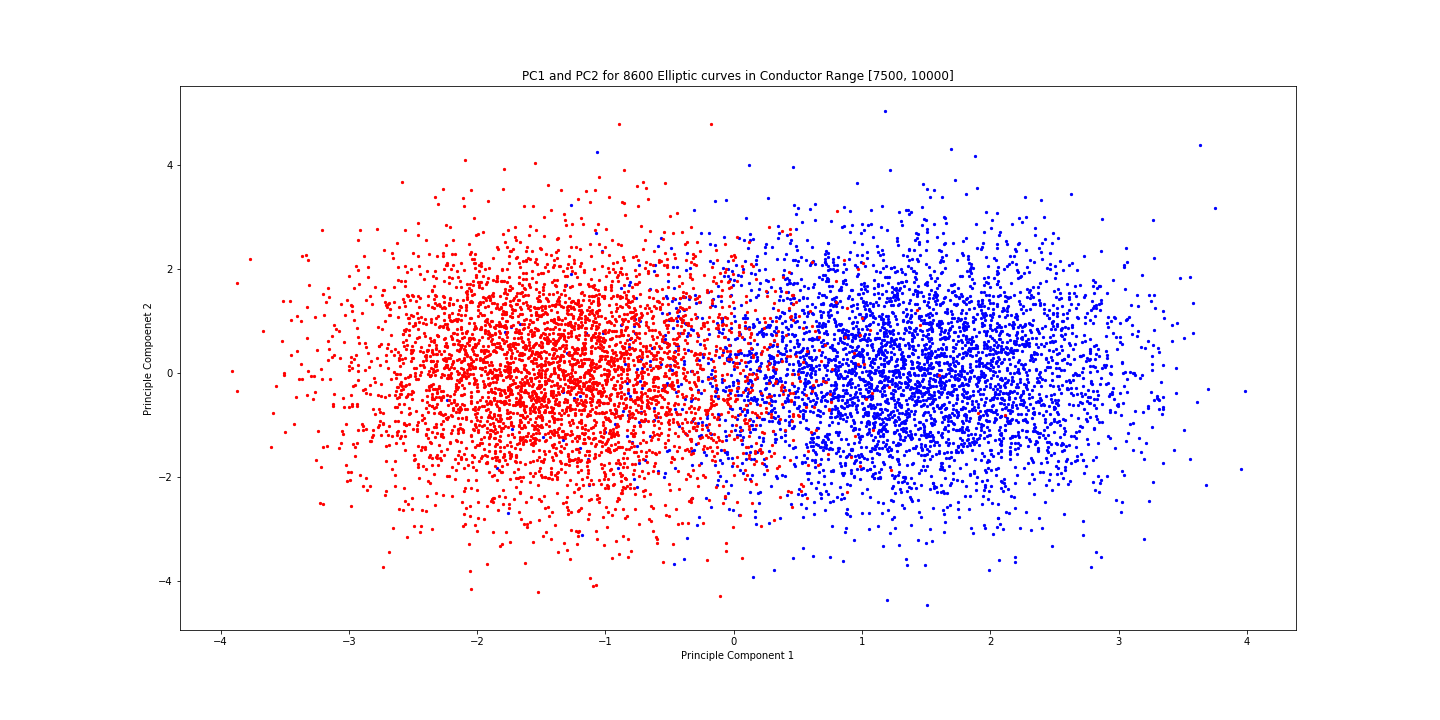
아래에 있는 그림은 차수 0과 차수 1 타원곡선 데이터셋에 대해 수행한 주성분 분석의 결과입니다. 컨덕터가 7,500에서 10,000 사이에 있는 타원곡선들 중 각 차수당 8,600개의 곡선을 사용했고, 차수가 0인 곡선들에 해당되는 점들은 파란색으로 차수가 1인 곡선들에 해당되는 점들은 빨간색으로 표시했습니다. 가로축인 첫번째 축을 따라 명확한 분리가 나타나는 것을 확인할 수 있습니다. 결국 기계학습을 통해 훈련된 모델은 가로축을 따라 파란점들과 빨간점들을 구별한다는 것을 이해할 수 있었습니다. 이 그림을 보니 고개가 끄떡여지고 기계학습 결과를 받아들일 수 있었습니다.

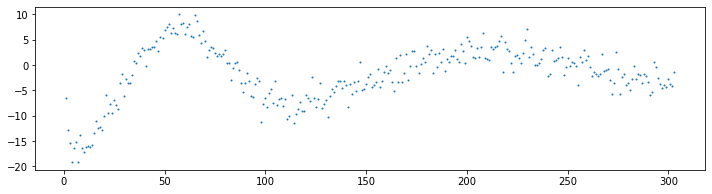
다음에 있는 그림은 첫 번째 축으로 사용된 벡터의 좌표들을 보여줍니다. 이 그림을 보면 300개의 소수들이 첫 번째 축을 결정하는데 있어 얼마나 기여했는지 알 수 있습니다. 여기서 잘 이해되지 않는 점이 있었습니다. 좌표들의 크기가 오르락 내리락 진동하는 것입니다. 즉, 소수들의 기여도가 일정하게 변하는 것이 아니라 예상 밖의 행동을 하고 있었습니다.

머머레이션    

이러한 진동현상은 고개를 갸우뚱거리게 만들었습니다. 이 진동이 무엇에서 비롯된 것일까요? 이 질문에 대한 답을 찾기 위해, 소수 $p$를 고정하고 특정 구간 $[N_1, N_2]$ 안에 컨덕터를 가지는 타원곡선들을 모아 각 차수 $r$ 별로 $a_p$ 값들의 평균을 계산해 보았습니다. 소수를 차례로 변화시키면서 이렇게 평균값을 계속 계산하면, $n$번째 소수를 가리키기 위해 도입한 지표 $n$을 변수로 하는 함수가 각 $r$에 대해 아래와 같이 정의됩니다.

$$f_r(n) = \frac{1}{\#\mathcal{E}_r[N_1,N_2]} \sum_{E \in \mathcal{E}_r[N_1,N_2]} a_{p_n}(E)$$
여기서 $N_1 < N_2$들은 양수인 정수들이고, $\mathcal{E}_r[N_1,N_2]$는 타원곡선 중에서 차수가 $r$이고 컨덕터가 $[N_1,N_2]$ 범위에 속하는 곡선들의 집합이며, $\#\mathcal{E}_r[N_1,N_2]$는 그 집합의 원소의 개수, 그리고 $p_n$은 $n$번째 소수입니다. 타원곡선 $E$에 따라 $a_{p_n}$의 값이 달라지므로 명확히 하기 위해 $a_{p_n}(E)$라고 썼습니다. 보시다시피 말 그대로 $n$번째 소수 $p_n$에 대해 $a_{p_n}$ 값들을 평균하고 있는 것입니다.

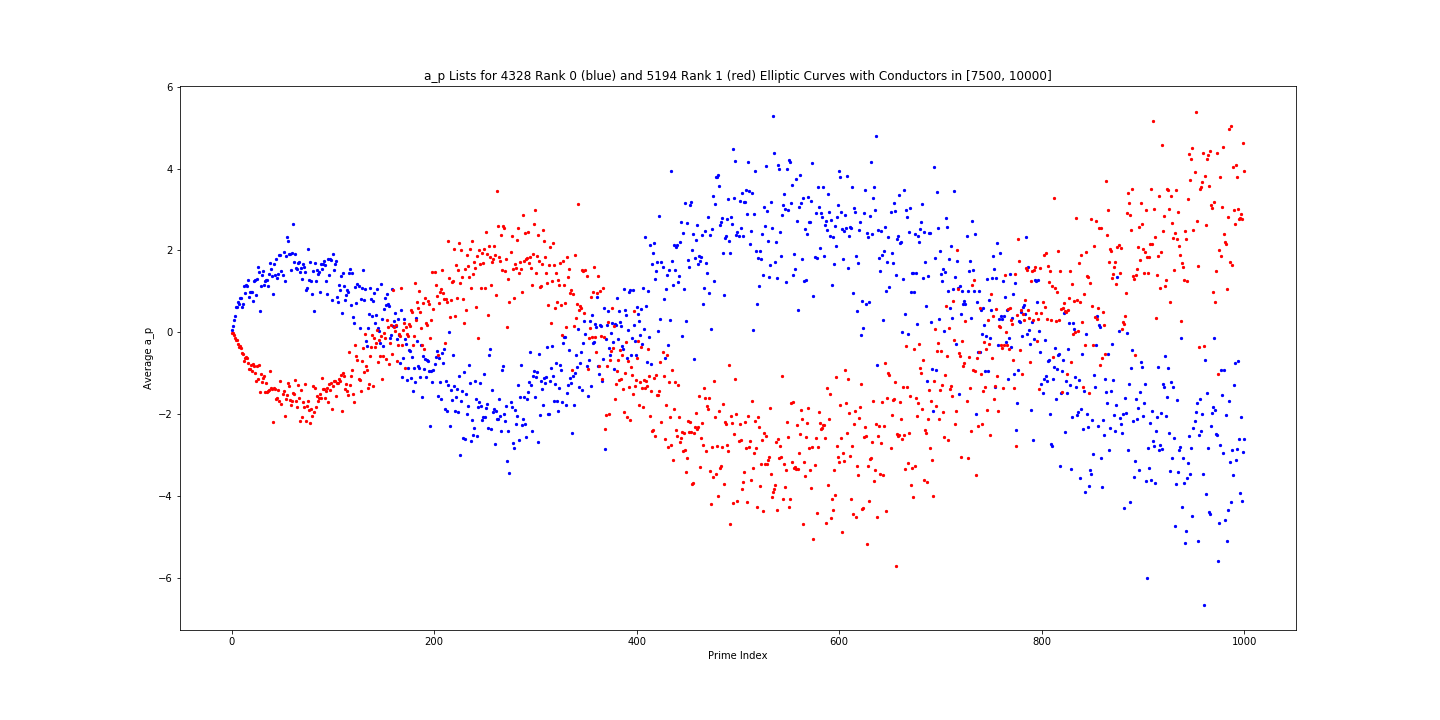
구체적으로, $[N_1,N_2] = [7500,10000]$ 구간을 생각하고 $1 \le n \le 1000$에 대해서, $f_0(n)$을 구해 파란색으로 $f_1(n)$은 빨간색으로 그래프를 그려 다음과 같이 비교해 보았습니다.

맨 앞에서 관찰되는 패턴은 놀라운 일이 아니었습니다. 차수 0에 해당되는 파란색 점들에 비해 차수 1에 해당되는 빨간색 점들이 아래에 있어야 한다는 것은 전문가들에게 이미 알려져 있는 사실이었습니다. 하지만, 컨덕터 범위가 정해져 있는 상태에서 소수들이 자꾸 커지면, 파란색 점들과 빨간색 점들이 교차하면서 위치를 바꾸고, 뿐만 아니라 계속 진행함에 따라 서서히 오르락 내리락 진동한다는 것은 누구도 예상하지 못했던 완전히 놀라운 결과였습니다. 애초에 기는 놈 위에 나는 놈 있어서 영원히 그럴 줄 알았는데, 때가 되면 세상이 완전히 뒤바뀌고 만다는 무슨 역사의 교훈을 보고 있는 것 같았습니다.

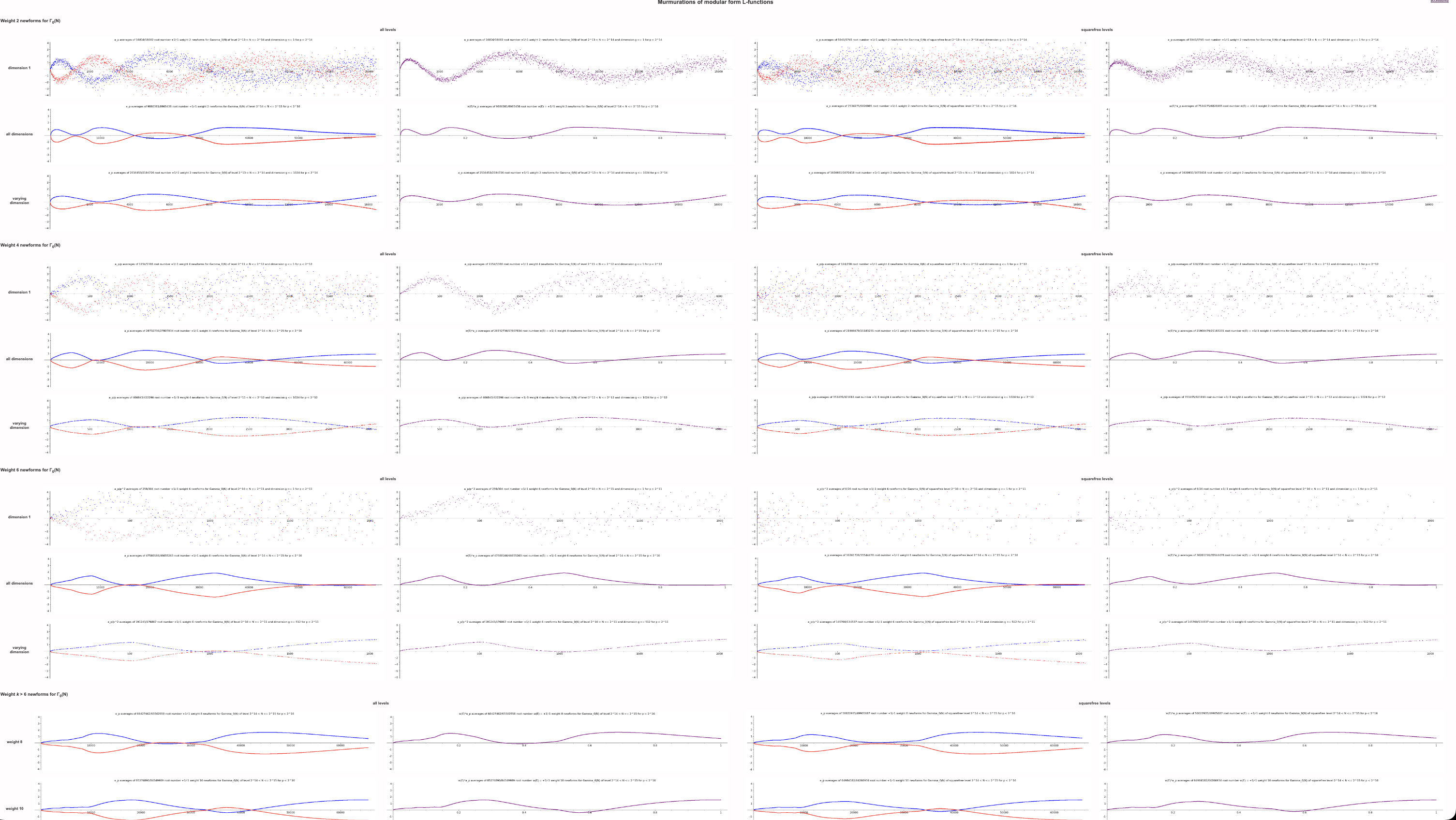
이 그림을 본 전문가들은 다들 충격을 받았고, 머머레이션이라고 불리기 시작한 이 현상에 대해 곧이어 중요한 질문들을 제기했습니다. 타원곡선이 가중치가 2인 보형형식^{modular form}에 해당되기 때문에 다른 가중치의 보형형식도 같은 현상을 보일지 궁금해했고, 또한 타원곡선이 종수^genus가 1인 곡선이므로 더 높은 종수를 갖는 곡선들도 비슷한 현상이 있을지 알고 싶어했습니다. 후속 연구로 알게된 그 답은 너무나 분명한 “예스^Yes”였습니다. 머머레이션 현상에 큰 관심을 가지게 된 MIT의 앤드류 서덜랜드(Andrew Sutherland)는 방대한 계산을 수행해 그 결과들을 모아 머머레이션 웹페이지[4] 를 운영하고 있습니다. 서덜랜드의 웹페이지의 스냅샷이 아래에 있습니다.

이 새로운 현상의 발견 소식은 학계에 빠르게 퍼졌습니다. 이 현상을 깊이 탐구하기 위해 전문가들이 모여 2023년 7월에 브라운대학의 계산실험수학연구소에서 머머레이션을 주제로 한 핫토픽 워크샵이 열렸고, 2024년 11월에 사이먼스 기하물리연구소에서 머머레이션에 초점을 맞춘 워크샵이 개최되었습니다. 이 발견은 퀀타 매거진^{Quanta Magazine}에도 소개되었습니다[5]. 이러한 관심 속에 여러 학자들이 머머레이션을 설명하는 이론, 엄밀한 증명, 그리고 개념의 확장에 몰두하게 되었습니다. 특히 프린스턴 대학과 미국 고등과학원의 겸임교수인 피터 사낙^{Peter Sarnak}은 머머레이션에 관한 전반적인 이론을 정리했고[2], 그의 제자 니나 주브릴리나^{Nina Zubrilina}는 보형형식에 대하여 머머레이션 현상을 엄밀히 증명하였습니다[3].

그 증명은 조화해석학에 기반을 둔 푸아송 합산 공식을 보형형식으로 일반화한 대각합 공식^{trace formula}에서 출발해서 해석학적 정수론의 여러 기법을 사용합니다. 또 머머레이션 현상을 $L$-함수 근들의 1차 밀도^{1-level density}가 상변이^{phase transition}할 때 일어나는 현상으로 이해할 수 있음을 설명합니다. 이런 결과들을 비롯하여 최근 2년 사이에 10편 가량의 논문들이 여러 학자들에 의해 발표되었습니다. 그럼에도 불구하고, 애초에 발견된 타원곡선의 머머레이션에 대해서는 바로 적용할 수 있는 대각합 공식이 없고, 종수가 더 높은 곡선들에 대해서는 아직 이해가 충분하지 않기 때문에 엄밀한 증명이 여전히 난제로 남아 있습니다. 해결의 실마리를 찾고 새로운 적용을 위해 머머레이션에 대한 연구는 지금도 활발히 진행 중입니다.

닫는 말

앞에서 우리는 기계학습 패러다임이 정수론에서 새로운 구조를 발견하는 일에 실제로 기여할 수 있음을 살펴보았습니다. 이는 한 가지 예로 보여 드린 것이고, 그 외에도 많은 성공적인 예들이 기하학과 위상수학, 조합론과 표현론, 그리고 편미분 방정식등 수학 전반에 걸쳐 이미 보고되어 있습니다. 앞으로도 더 많은 예들이 생기고 좀 더 다양한 기계학습 도구들도 사용하게 되면서 큰 발전이 있을 것으로 예상합니다.

현재까지의 모든 예들을 보면, 이 글의 시작에서 간단히 말씀드렸듯이, 기계학습을 이용한 수학연구의 모든 단계에서 아직은 인간 수학자의 개입이 필수적입니다. 컴퓨터와 기계학습은 수학연구를 도와주는 강력하고 유용한 도구로 활용될 뿐입니다. 각 단계가 수학적 이해와 지식 뿐아니라 특정한 선택과 직관을 요구하기 때문에 이를 자동화하는 것은 현재로서는 어려워 보입니다. 따라서, 적어도 지금 당장은 기계가 수학자를 대체할 위험이 없고, 오히려 수학자들은 새로운 강력한 도구가 생겼으니 새 장난감을 선물받은 어린 아이처럼 신나는 상황입니다. 많은 연구자들과 학생들이 동참해서 수학연구에 새로운 황금기가 도래하기를 바라봅니다.