9월 퍼즐에 참여해주신 분들께 모두 감사드리며,
참여해주신 분들 중 정답과 함께 좋은 풀이를 보내주신
온준엽 님에게 문화상품권을 전달하겠습니다.
9월의 퍼즐 문제
다음은 KPP 이충명님의 풀이입니다.
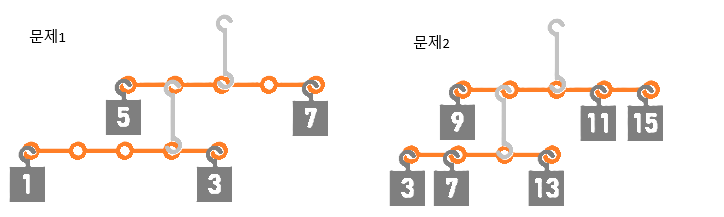
1번 풀이
아래쪽 막대에 추 3개를 달고, 위쪽 막대에 아래쪽 막대와 추 1개를 단다면, 아래쪽 모빌의 추 3개의 무게 합이 위쪽 모빌의 추 1개와 정수 배 (정확히는 1배, 2배, 혹은 3배) 관계여야 한다. (1+3+5)와 7, (1+3+7)과 5, (1+5+7)과 3은 정수 배 관계가 아니며, (3+5+7)과 1은 정수 배 관계이지만 1:15의 비율을 만들기에는 막대 길이가 부족하여 모빌의 평형을 맞출 수 없다.
따라서 아래쪽 막대에 추 2개를 달고 위쪽 막대에 아래쪽 막대와 추 2개를 달아야 한다. 이 경우 아래쪽 막대의 추 2개의 무게는 정수 배 (정확히는 1배, 2배, 혹은 3배) 관계여야 하므로 1과 3을 달아야만 하고, 위쪽 막대에 (1+3)과 5와 7을 모빌에 매달아서 평형을 맞추려면 다음 방법밖에 없다.
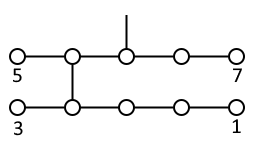
2번 풀이
가장 먼저, 모빌에 빈 칸이 6개 생기고 추도 6개이므로 모든 칸이 꽉 차야 한다는 사실을 관찰할 수 있다. 그리고 모든 추의 무게가 홀수라는 점에 주목하자.
5칸짜리 막대를 아래에 두어 추 4개를 단다면 그 무게의 총합은 짝수다. 그러면 홀짝을 따져보았을 때 위에 둔 4칸짜리 모빌이 다음과 같아야 평형을 맞출 수 있다.
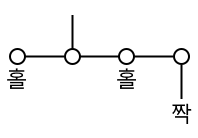
그러나 이것은 오른쪽이 과하게 무거울 것이 분명하므로 불가능하다. 따라서 5칸짜리 막대가 위로 가야 한다. 이제 아래쪽 4칸짜리 막대를 보자.
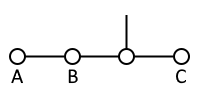
B와 C의 차이가 2A여야 한다. 만약 B에 3을 사용한다면 B와 C의 차이는 아무리 커도 12인데, 남은 추 중에 무게 6 이하의 추가 없으므로 A에 매달 추가 없다. 따라서 A가 3이고 B와 C의 차이는 6이어야 한다. 즉, (A, B, C) = (3, 7, 13)과 (3, 9, 15) 두 가지만 가능하다. 이때 무게 합은 각각 23과 27이며, 둘 다 홀수다.
이제 위쪽 5칸짜리 막대를 보자. 홀짝을 따져보았을 때 위에 둔 5칸짜리 막대가 다음과 같아야 평형이 맞는다.
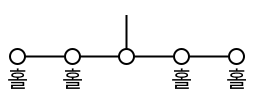
4개의 홀수 중 어느 것이 아래쪽 막대에 해당할지 아직은 알 수 없다.
이제 (23, 9, 11, 15)나 (27, 7, 13, 15)를 가지고 위쪽 5칸짜리 막대를 채우면 다음과 같이 평형을 찾을 수 있다.
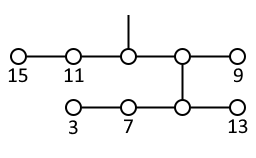
다음은 정답자로 선정된 온준엽님의 풀이입니다.
맨 아래쪽 모빌부터 균형을 맞추는 경우를 모든 경우를 브루트 포스로 구하면, 각 모빌에 대해 한 단계 위 모빌은 아래 모빌에 사용된 추 들의 무게 합을 하나의 추로 취급할 수 있습니다. 이런 식으로 맨 위쪽 모빌까지 재귀적으로 해결하는 알고리즘을 생각할 수 있습니다. 한 단계씩 올라갈 때 마다 사용 가능한 추의 개수는 적어도 하나 줄고, 가로막대의 개수도 하나씩 감소하므로, 이 알고리즘은 반드시 종료됩니다.
문제 1과 문제 2 에서 그림에 제시된 답안 또는 그림에서 0개 이상의 가로막대를 180도 회전시킨 경우에만 답이 됩니다. 각 경우를 서로 다른 답이라고 간주하면, 문제 1과 문제 2 각각에는 4가지의 답이 존재합니다.