현대암호학의 태동 [3]: 디피와 헬만의 “암호학의 새로운 방향”

1976년, 디피^{Whitfield Diffie; 1944~}와 헬만^{Martin Hellman; 1945~}은 제목부터 심상치 않은 논문 <New Directions in Cryptography^{암호학의 새로운 방향}> [1] 으로 세상을 놀라게 했다. 마치 선언문처럼 “우리는 지금 암호학 변혁의 문턱 위에 서 있다.¹”라는 문장으로 시작하는 이 논문에서 둘은 공개키 암호^{Public Key Cryptography}라는 혁신적인 패러다임을 제시하고, 디피–헬만 키교환 프로토콜을 통해 이를 부분적으로 구현했다. 이 개념들은 오늘날 인터넷 보안의 핵심을 이루고 있으며, 온라인에서 한 번이라도 안전하고 편리하게 결제를 해봤다면, 모두 디피와 헬만에게 빚을 지고 있는 셈이다. 실제로 이 논문은 암호학에 변혁을 가져왔고, 이 공로로 두 사람은 전산학의 노벨상이라 불리는 튜링상을 수상했다. 이번 글에서는 디피와 헬만이 제시한 “암호학의 새로운 방향”을 함께 살펴보고자 한다. 우선, 그들이 등장하기 직전의 시대상을 잠시 돌아보자.

컴퓨터와 전산학의 발전

60년대를 거쳐 1970년대에 들어서면서 컴퓨터는 눈부시게 발전했다. 연산 속도는 기하급수적으로 빨라지고, 가격은 꾸준히 하락했으며, 더 작고 널리 보급되는 방향으로 진화했다. 1970년대는 아직 PC가 대중화되기는 전이었지만, 60년대 메인프레임을 거쳐 미니컴퓨터가 대학 연구소나 중소기업에도 보급되기 시작한 시기였다. 기업과 정부 기관은 대규모 데이터 처리를 위해 컴퓨터를 적극 도입했고, 민간에서도 전자통신망을 통해 정보를 주고받는 일이 점점 일상화되었다. 컴퓨터는 더 이상 일부 연구실에만 머무는 장비가 아니라, 사회 전반을 지탱하는 기반 기술로 자리 잡아 가고 있었다. 특히 인터넷의 전신인 ARPANET이 등장하고 발전하면서 컴퓨터 간 네트워크 연결의 새로운 가능성이 열렸고, 정보의 교환과 공유가 곧 한층 새로운 차원으로 확장될 것임이 분명해진 시점이었다.

이에 발맞춰 전산학도 눈부신 발전을 거듭했다. 그중에서도 계산복잡도 이론^{Complexity Theory}과 알고리즘 연구는 특히 주목할 만하다. 튜링과 그 후속 세대가 마련한 탄탄한 이론적 토대 위에서 학자들은 어떤 문제가 계산 가능한지, 계산할 수 있다면 얼마나 효율적으로 해결할 수 있는지, 그리고 그 효율성에 이론적 한계가 존재하는지 등을 연구했다. 전통적인 수학 문제에서 ‘해의 존재 여부’와 같은 고전적 질문을 넘어, 이제는 해를 얼마나 효율적으로 계산할 수 있는지와 같은 계산적 관점이 중요한 연구 주제로 떠올랐다. 다시 말해, 가능성과 불가능성을 넘어 쉬움과 어려움, 즉 현실적 가능성과 현실적 불가능성을 다룰 수 있는 탄탄한 이론적 토대가 구축된 셈이다.

컴퓨터의 대중화와 인터넷의 탄생이라는 흐름 속에서 자연스럽게 암호 기술에 대한 수요는 급격히 증가했다. 그러나 당시의 암호학은 이러한 요구를 충분히 충족시킬 수 없었다. 대규모 네트워크 환경에서의 확장성 문제에 더해, 인터넷이 가능케 할 전자상거래와 같은 새로운 시나리오를 충분히 지원할 수 없다는 한계도 존재했다. 디피-헬만 이전 암호학이 지닌 이러한 한계를 좀 더 자세히 살펴보자.

대칭키 암호의 한계

우선 지금까지 살펴본 암호화 스킴들을 떠올려보자. 1편에서 다룬 시저 암호와 치환 암호, 그리고 2편에서 다룬 원타임패드까지 모두 같은 구조를 따른다. 바로 이들 스킴에는 하나의 비밀키만 존재하며, 송신자가 암호화할 때와 수신자가 복호화할 때 같은 비밀키를 사용한다는 점이다. 시저 암호에서는 알파벳을 얼마나 밀지, 치환 암호에서는 치환표, 원타임패드에서는 난수열이 바로 이 비밀키의 역할을 하며, 암호화와 복호화 과정 모두에 사용된다. 2차 세계대전 독일군이 사용했던 에니그마를 비롯하여 디피-헬만 이전의 모든 암호화 스킴이 그러했다. 이러한 암호화 스킴들은 이제 디피-헬만의 공개키 암호와 대비해 대칭키 암호^{Symmetric Key Encryption}라고 불린다. 송신자와 수신자가 같은 키를 사용하여 대칭적이라는 의미에서 이름이 붙었다.

이러한 대칭키 암호에서는 송신자와 수신자가 같은 비밀키를 사용해야 하므로, 각 통신 쌍은 사전에 안전하게 키를 교환해야 하는 문제가 있었다. 예를 들어, 멀리 떨어져 있는 A와 B가 비밀 대화를 나누고 싶지만 서로 공유해둔 비밀키가 없다고 가정해보자. 대칭키 암호만으로는 이 문제를 해결할 수 없다. A가 비밀키를 B에게 안전하게 전달하려 해도, 그 과정 자체가 안전하기 위해서는 이미 공유된 비밀키가 필요하다. 결국 문제는 끝없이 되풀이되는 도돌이표와 같은 상황이 된다.

결국 당시 비밀키를 교환할 방법은 두 가지뿐이었다. 직접 만나거나, 신뢰할 만한 제3자를 통해 전달하는 것이다. 실제로 1970년대 미국 정부와 군은 COMSEC이라는 전담 기관을 두고 매일 비밀키를 전달했지만, 이는 막대한 비용을 감수해야만 가능한 방식이었다. 민간이 따라 하기에는 턱없이 비효율적일 뿐 아니라, 제3자를 통한 전달에는 본질적인 신뢰 문제가 따랐다. 무엇보다 키 교환은 항상 가장 취약한 고리였다. 교환 과정에서 비밀키가 유출되면, 암호는 그대로 무력화되기 때문이다. 네트워크 규모가 커질수록 문제가 더 심각해질 것은 분명했다. 예를 들어 $n$명이 모두 서로 안전하게 통신하려면 총 $\frac{n(n-1)}{2}$개의 서로 다른 비밀키를 교환하고 관리해야 한다. 게다가 안전성을 위해 비밀키를 주기적으로 갱신하는 것까지 고려한다면 부담은 더 늘어난다. 결국 컴퓨터와 네트워크의 확산은 기존 대칭키 암호화 방식이 지닌 구조적 한계를 적나라하게 드러냈다.

또한, 컴퓨터의 대중화와 인터넷의 탄생이라는 흐름 속에서 등장한 새로운 시나리오들은 기존 암호학이 답할 수 없는 질문들을 던졌다. 예컨대, 온라인에서 새롭게 만난 상대와 비밀 대화를 나누거나 전자상거래를 하고 싶다면 어떻게 해야 할까? 이는 단순히 비용의 문제가 아니라, 도청자가 존재하는 상황에서 물리적 매개체 없이 안전하게 키를 교환할 수 있을지를 묻는 새로운 종류의 질문이었다. 또한 인증^{Authentication}의 문제도 새롭게 제기되었다. 내가 받은 메시지가 정말 특정 사람으로부터 온 것임을 어떻게 확인할 수 있을까? 기존 암호학은 이러한 문제에 답하지 못했다. 하지만 당시에는 이러한 기존 암호학의 제약이 해결해야 할 과제라기보다는, 암호 자체의 근본적 한계로 받아들여졌다.

공개키 암호의 등장

이런 흐름 속에서 암호학의 가능성을 재고하며 기존 고정관념에 도전한 이들이 바로 디피와 헬만이다. 이들은 컴퓨터와 인터넷의 발전 앞에서 대칭키 암호가 맞닥뜨린 한계와 이를 돌파할 방법을 수년에 걸쳐 탐구했고, 수많은 시행착오 끝에 공개키 암호^{Public Key Cryptography}라는 혁신적인 발상에 도달했다. 이들의 핵심 아이디어는 암호화 키와 복호화 키를 분리^decouple하는 것이었다. 즉, 암호화와 복호화에 꼭 같은 키를 사용할 필요가 없다는 것이다. 이는 물리적 자물쇠에 빗대어 이해할 수 있다. 문을 닫으면 자동으로 잠기지만 열 때는 비밀번호가 필요한 전자식 도어락, 혹은 잠글 때는 약간의 힘만으로 철컥하고 잠기지만 열 때는 열쇠가 필요한 자물쇠와 같은 구조다. 이 구조를 암호에 적용해보자면, 누구나 공개키(암호화 키)를 이용해 수신자에게 메시지를 암호화해 보낼 수 있지만 그 메시지를 복호화할 수 있는 사람은 오직 대응하는 비밀키(복호화 키)를 가진 수신자뿐인, 이것이 바로 키교환이 필요 없는 공개키 암호시스템^{Public Key Encryption}이다. 더 나아가, 디피와 헬만은 이 아이디어를 역으로 적용하면 네트워크상의 인증 문제 또한 해결할 수 있다는 통찰을 얻었다. 서명은 오직 비밀키를 가진 본인만이 생성할 수 있고, 그 진위는 공개키를 가진 누구나 검증할 수 있는, 물리적 서명의 이상적인 대응으로서 전자서명^{Digital Signature}의 개념이 처음 제시되었다. 많은 위대한 발견이 그렇듯, 지금에서야 단순하고 자명해 보이지만 당시에는 고정관념의 벽에 가로막혀 그 가능성을 눈치챈 이가 없었다.

디피와 헬만은 공개키 암호화 스킴의 핵심을 일방향 트랩도어 함수^{One-way Trapdoor Function}라는 수학적 구조로 추상화했다. 이 함수는 입력값을 가지고 출력값을 계산하는 것은 누구나 쉽게 할 수 있지만, 출력값만 알고는 원래 입력값을 찾아내는 것이 매우 어렵다(일방향성). 다만 특정한 비밀 정보^trapdoor를 알고 있으면 원래 입력값을 쉽게 되찾을 수 있다. 이런 함수의 정의^description를 공개키로, 트랩도어 정보를 비밀키로 삼고, 함수를 계산하는 과정을 암호화에, 역함수 계산을 복호화에 대응시키면 곧바로 공개키 암호화 스킴이 된다. 결국 디피-헬만에게 남은 과제는 안전한 일방향 트랩도어 함수를 설계하는 일뿐이었다.

이산로그 문제

아쉽게도 디피와 헬만은 자신들이 제시한 공개키 암호라는 비전을 직접 완성하지는 못했다. 공개키 암호라는 방향에는 확신이 있었지만, 결국 안전한 일방향 트랩도어 함수를 찾아내지는 못한 것이다. (하지만 얼마 지나지 않아, 리베스트^Rivest-샤미르^Shamir-애들먼^Adleman이 그 유명한 RSA 공개키 암호화 스킴을 설계하면서 이를 실현하게 되는데, 이는 다음 글에서 살펴보도록 하자.) 대신 디피-헬만은 다소 제한된 형태의 공개키 암호를 구현함으로써 기존 대칭키 암호의 키 분배 문제를 해결하였는데, 그것이 바로 키교환 프로토콜이다. 디피-헬만 키교환 프로토콜을 살펴보기 전에, 먼저 이 프로토콜의 바탕이 되는 이산로그 문제^{Discrete Logarithm Problem}를 살펴보도록 하자.

이산로그 문제는 고정된 소수 $q$와 어떤 정수 $g$에 대해 랜덤한 $h$가 주어졌을 때, $h\equiv g^k \pmod{q}$를 만족하는, 즉 $h$와 $g^k$가 $q$로 나눈 나머지가 같아지는 자연수 $k$를 찾는 문제이다. 이는 $\mathbb{Z}_q$의 곱셈군^{multiplicative group} $\mathbb{Z}^{\times}_q$에서 정의된 이산로그 문제이며, 더 일반적으로, 이산로그 문제는 고정된 순환군 $(G,\times)$와 그 생성원 $g$에 대해 랜덤한 $h=g^k$가 주어졌을 때 $k$를 계산하는 문제로 정의할 수 있다. 모든 이산로그 문제가 어려운 것은 아니며, 예를 들어 단순한 덧셈군 $(\mathbb{Z}_p,+)$에서는 자명하다. 하지만, “적절히” 선택된 유한군 $G$에 대해서는 이산로그 문제가 수십 년간 수많은 연구자의 노력에도 불구하고 효율적인 알고리즘을 찾지 못했기에, 이산로그 문제는 암호학적 난제로 여겨진다. 오늘날에는 타원곡선군이라는 구조에서 정의된 이산로그 문제가 암호에서 널리 활용되고 있다. 관심 있는 독자는 이철희 박사님의 Horizon 시리즈 <비트코인 속으로 들어간 타원곡선>을 참고해 보는 것도 좋겠다.

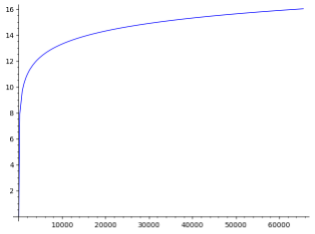
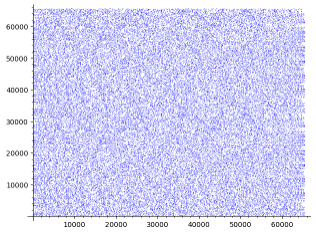
이 단순한 문제가 어렵다는 사실(혹은 믿음)이 현대 인터넷 보안의 초석을 이루고 있다. 왜 어렵냐고 묻는다면 사실 딱히 말할 수 있는 건 많지 않다. (쉽다는 것은 보여주기 쉽지만, 어렵다는 것을 주장하기는 늘 어렵다). 다만 실수에서의 로그 계산과 비교해 봄으로써, 어느 정도 직관적으로 이해해 볼 수 있다. [그림 3] 은 실수에서의 밑 2 로그 함수의 그래프이고, [그림 4] 는 mod 65543에서 밑 2에 대한 이산로그 값들을 플로팅 한 것이다. 실수에서 로그 계산이 쉬운 이유는 로그 함수가 단조 증가하기 때문에, 몇 번의 시도만으로도 대략적인 크기를 가늠하고 탐색 범위를 좁혀 나갈 수 있기 때문이라고 생각해 볼 수 있다. 반면, 이산로그 그래프를 보면 랜덤해 보인다. 몇 개의 값을 시도해 본다고 해서 다른 값들에 대한 어떤 힌트를 얻을 수 있는지 불분명하다. 이러한 맥락에서, 전수조사처럼 하나씩 확인하는 것보다 유의미하게 더 효율적인 방법을 고안해 내기는 쉽지 않아 보인다. 참고로, 예시에서 사용한 65543은 실제 암호에서 사용하는 군 $G$의 최소 크기인 $2^{256}$보다 훨씬 작다. 실제 암호에서 사용되는 군이라면, 이런 플로팅조차 현실적으로 불가능하다.

이 정도의 설명으로는 이산로그가 어렵다는 것을 쉽게 받아들이지 못할 수도 있다. 이런 경우에는 직접 부딪혀 어려움을 몸소 체험해 보는 수밖에 없다. 심지어 상금(?)이 걸려있는 이산로그 문제들도 있으니, 한 번 직접 도전해 보시길! 바로 비트코인 창시자인 사토시^{Satoshi Nakamoto; ?~?}가 홀연히 사라지면서 15년 넘게 주인 없이 묶여있는 코인들이다. 그 양이 최소 100만 비트코인에 달하며, 이 글을 작성하고 있는 시점 기준 약 150조 원 규모이다. 현재는 상황이 약간 달라졌지만, 초창기 비트코인 거래의 보안은 전적으로 이산로그 문제의 어려움에 의존했다. 따라서 만약 이를 효율적으로 풀 수 있다면 이 막대한 양의 코인을 마음대로 할 수 있는 셈이다. 이산로그 문제를 일반적으로 풀 필요는 없고(사실 이는 불가능함이 증명되어 있다), 비트코인에서 사용하는 특정한 타원곡선 위의 이산로그만 빠르게 풀 수 있다면 된다. 심지어 모든 인스턴스를 해결할 수 있을 필요도 없다. 예컨대 비트코인의 첫 채굴 보상에 해당하는² [그림 5] 속 문제 인스턴스 하나만 풀어도 50비트코인, 시가로 75억 원가량을 손에 넣을 수 있다. 아이러니하게도, 이 단순한 산수 문제 하나에 걸려 있는 돈이 리만 가설에 공식적으로 걸린 상금보다도 훨씬 크다. 혹시라도 이 문제를 푼다면, 필자가 소개해 줬다는 사실을 꼭 기억해 주길… 농담이다. 다만 이 예시가 전 세계 암호학자들이 이산로그 문제의 어려움에 얼마나 강력한 확신이 있는지를 보여주는 단서가 되었으면 한다.

디피-헬만 키교환 프로토콜

디피와 헬만은 이산로그 문제의 어려움을 바탕으로, 도청자가 존재하더라도 안전하게 공유 비밀 키를 생성할 수 있는 방법을 제시했다. 이것이 바로 디피-헬만 키교환^{Diffie-Hellman Key Exchange} 프로토콜이다. 이 프로토콜을 이용하면, 통신 당사자들이 사전에 어떤 비밀 정보도 공유하지 않고도 공개된 네트워크를 통해 안전하게 공유 비밀키를 함께 만들어낼 수 있다. 즉, 키 교환 프로토콜은 기존 대칭키 암호의 키분배 문제를 해결했다. 이는 디피-헬만 이전에는 불가능하다고 여겨졌던, 실로 놀라운 성과이다. 다만, 키교환 프로토콜은 공개키 암호라는 그들의 원대한 비전과 비교하면 몇 가지 한계를 지닌다. 먼저 공개키 암호는 공개 키만 알면 언제든 메시지를 보낼 수 있지만, 키교환 프로토콜은 통신 당사자들이 직접 참여해야만 성립한다. 이 때문에 키교환 과정은 반드시 두 사람이 동시에 온라인 상태여야만 이루어질 수 있다. 그리고 키교환 프로토콜은 그 과정에서 통신 상대가 실제로 내가 통신하고자 하는 사람인지 검증할 수 있는 추가적인 인증 절차가 필요로하다는 미묘한 지점도 존재한다.

디피-헬만 키 교환 프로토콜은 비교적 간단하며, 그 과정은 다음과 같다. 예를 들어, 앨리스^Alice와 밥^Bob이 안전한 통신을 위해 사전에 키 교환을 수행한다고 가정해 보자.

1. 공개 파라미터 설정: 먼저 앨리스와 밥은 함께 이산로그 문제가 어려운 소수 $q$와 생성원 $g$를 결정한다.
2. 개인키 생성: 앨리스와 밥은 각자 무작위로 개인키로 사용할 정수 $a$와 $b$를 하나씩 선택한다. 이 개인키들은 오직 본인들만 알고 있고, 외부에는 절대 노출하지 않는다.
3. 공개키 교환: 앨리스와 밥은 각자 자신의 공개키 $A \equiv g^a \pmod{q}$와 $B \equiv g^b \pmod{q}$를 계산하여 서로에게 전송한다.
4. 공유 비밀키 생성:
   • 앨리스는 밥으로부터 받은 공개키 $B$를 이용하여 공유 비밀키 $s\equiv B^a\pmod{q}$를 계산한다.
   • 밥은 앨리스로부터 받은 공개키 $A$를 이용하여 공유 비밀키 $s\equiv A^b\pmod{q}$를 계산한다.

이 과정을 통해 앨리스와 밥이 같은 비밀키 $s$를 공유하게 된다는 것은 다음과 같이 쉽게 확인할 수 있다.

$$B^a \equiv (g^{b})^a \equiv (g^{a})^b \equiv A^b \pmod{q}$$

이제 이들의 통신을 관찰하는 도청자가 있다고 가정해 보자. 도청자는 통신 과정에서 오고 간 $q$, $g$, $A$, $B$를 모두 알 수 있지만, 이산로그 문제의 어려움 때문에 $A$와 $B$로부터 개인 키 $a$와 $b$를 알아낼 수 없다. 따라서 도청자는 공유 비밀 키 $s$를 계산할 수 없으며, 앨리스와 밥은 도청자의 존재에도 불구하고 안전하게 공유 비밀 키를 생성할 수 있게 된다.³

암호학의 새로운 방향

사람들이 디피–헬만을 현대 암호학의 기점으로 꼽는 이유는 여러 측면에서 찾아볼 수 있다. 무엇보다, 디피–헬만의 논문은 암호학의 역할과 범위를 근본적으로 확장했다. 디피–헬만 이전의 암호학은 대칭키 암호화 스킴이라는 단 하나의 문제에만 집중되어 있었다. 그러나 디피와 헬만은 기존의 틀을 깨고, 암호학이 지닐 수 있는 무궁무진한 가능성을 드러냈다. 대칭키를 넘어 공개키 암호화 스킴, 키 교환 프로토콜, 전자서명까지. 결국 암호학이 성취할 수 있는 것을 가로막고 있던 것은 우리의 미흡한 상상력에 불과하다는 메시지를 던진 것이다.

다음으로 주목할 점은, 암호 설계에서 수학적 난제를 적극적으로 활용하기 시작했다는 것이다. 예를 들어, 디피-헬만 키교환은 계산수론의 난제인 이산로그 문제를 바탕으로 한다. 이전 글들에서 언급했던 에드거 앨런 포의 문장, “인간 지성이 고안한 모든 암호는 결국 인간 지성에 의해 해독될 수밖에 없다.”를 떠올려보면, 인간 지성이 완전히 새로운 암호를 바닥부터 고안하기보다는, 우주에 이미 존재하는 자연스러운 수학 난제들을 기반으로 암호를 설계하는 새로운 접근이 제시되었다고 이해할 수 있다. 이 지점에 대해서는 다음 글들에서 더 깊이 다룰 예정이다.

조금 다른 맥락에서의 의의도 있다. 산업계의 관심이 점차 커지고 있긴 했지만, 당시 암호 기술은 주로 군사 및 첩보 목적에 집중되어 있었다. 디피와 헬만이 활동하던 미국에서는, 한국의 국가정보원에 해당하는 NSA^{National Security Agency}에서 암호 관련 지식을 독점하고 있었다. 천문학적인 수준의 예산을 투입해 우수한 연구자들을 다수 고용했으며, 그 결과물들은 모두 기밀로 처리되어 내부에서만 공유되었다. 이런 상황에서 대부분의 사람은 민간에서의 암호 연구가 의미 있는 성과를 내기 어렵다고 생각했으며, 설사 성과를 얻더라도 기존 NSA 연구의 재발견에 그칠 것이라는 회의론이 팽배했다. 하지만 디피와 헬만은 이런 회의론에 굴하지 않았고, 비록 재발견일지라도 일부 집단에만 독점된 지식을 세상에 알리는 가치가 있다고 믿었다. 이러한 제한된 환경 속에서, 외로운 싸움 끝에 인류문명사에 획을 그은 디피와 헬만의 집념은 큰 감동을 준다. 디피와 헬만도 이 지점을 강조하며 논문을 다음과 같이 끝맺는다.

“이 논문이, 정부의 독점으로 제약받아 온 암호학이라는 매혹적인
분야에 더 많은 이들이 도전하도록 불씨를 지피기를 바랍니다.⁴“

다음 글에서는 예고한 대로, 리베스트-샤미르-애들먼이 이후 이들의 이름 이니셜을 따 ‘RSA’라 불리게 된 최초의 공개키 암호 스킴을 설계하며 디피와 헬만의 비전을 완성하는 장면을 살펴보도록 하자.