표준기저를 찾아서 [5]

들어가며

우리는 본 연재 시리즈를 통하여 벡터공간 혹은 대수의 표준기저라는 개념에 대하여 살펴보고 있다. 벡터공간은 더하기와 상수곱이 주어진 집합, 대수는 이에 더하여 원소 간 곱하기가 주어진 집합이다. 벡터공간의 모든 원소를 표현할 수 있게 해주는 가장 작은 집합이 기저인데, 우리는 기저들 중 가장 표준적인 것이 무엇인지에 대해 고찰해 왔고, 표준기저를 찾는 방법론 중 범주화라는 방법과 그 예시를 살펴보았다. 이번 글에서는 지난 연재글들에서 제기된 문제나 논의들을 마무리하며 시리즈를 끝마치고자 한다.

첫 번째 연재글에서 제시한 문제

첫 번째 연재글([1])에서 제시한 문제로 되돌아가 보자. 우리는 먼저 기초적인 예시로 다변수 유리계수 로랑 다항식 대수 $\mathbb{Q}[x_1^{\pm 1}, x_2^{\pm 1}, \ldots x_N^{\pm 1}]$를 고려했었다. 로랑 다항식이란 다항식의 일반화로, 변수들의 음의 정수 지수까지 허용한 다항식을 말하며, 예시로는 $ – \frac{2}{3} x_1^4 x_3^{-1} + \frac{5}{2} x_2^2 x_3^{-2} x_4+ \frac{1}{4}$이 있겠다. 참고로 다변수 유리계수 로랑 다항식 대수는 표준기저를 가진다고 주장했던 바 있다.

우리는 첫 연재글([1]) 말미에서 이변수 로랑 다항식 대수 두 개를 풀칠하여 만든 대수를 고려했었다. 편의를 위하여 변수의 이름을 살짝 바꿔서 이변수 로랑 다항식 대수 $\mathbb{Q}[X_1^{\pm 1}, X_2^{\pm 1}]$과 $\mathbb{Q}[Y_1^{\pm 1}, Y_2^{\pm 1}]$을 서로 붙인다고 생각할 수 있고, 붙이는 데에는 다음의 공식을 사용하였다:$$X_1 = Y_1^{-1}, \qquad X_2 = Y_2(1+Y_1).$$두 대수를 붙여서 얻어지는 대수로서는$$\mathcal{A}_1 = \mathbb{Q}[X_1^{\pm 1}, X_2^{\pm 1}] \cap \mathbb{Q}[Y_1^{\pm 1}, Y_2^{\pm 1}],$$ 즉 좀 더 정확히는 $X_1,X_2$에 관한 유리계수 로랑 다항식 중에서, 위의 풀칠 공식을 이용해 $Y_1,Y_2$에 관하여 바꿔 썼을 경우에도 로랑 다항식이 되는 것들을 모두 모은 집합을 고려했었다. [1] 에서 들었던 예시로, $X_1^{-2} + X_1X_2 – 1$은 $X_1,X_2$에 관한 로랑 다항식이면서, $X_1,X_2$ 자리에 $Y_1^{-1}, Y_2(1+Y_1)$을 집어넣어 정리해보면, $Y_1^2$ +$Y_1^{-1} Y_2$+$Y_2 -1$이므로 $Y_1,Y_2$에 관한 로랑 다항식이 된다. 따라서 $X_1^{-2} + X_1X_2 – 1$은 $\mathcal{A}_1$의 원소이다. 반면 $X_1X_2^{-1}$은 $X_1,X_2$에 관한 로랑 다항식이기는 하지만, $Y_1,Y_2$에 관하여 나타내어 보면 $\frac{1}{Y_1Y_2(1+Y_1)}$이므로 $Y_1,Y_2$에 관하여 유리식이기는 하지만 로랑 다항식은 아니므로, $X_1X_2^{-1}$은 $\mathcal{A}_1$의 원소는 아니다. 이렇게 모든 `이중’ 로랑 다항식들의 집합으로 정의된 $\mathcal{A}_1$이 유리수체 위의 벡터공간이며 나아가 대수를 이룬다는 것, 즉 더하기와 유리수 상수곱, 그리고 곱하기에 닫혀 있다는 사실은 쉽게 볼 수 있다. [1] 에서는 이 대수 $\mathcal{A}_1$의 벡터공간으로서의 기저를 찾아보라는 문제, 더 나아가서는 표준기저가 있는지 생각해보라는 문제를 제시했었다.

사실을 고백하자면 필자도 현재 이 문제에 관한 좋은 답을 알지 못한다. 그럼에도 오히려 일견 이 문제보다 한 단계 더 어려워보이는 문제를 고려해보고자 한다. 이번에는 이변수 로랑 다항식 대수 세 개 $\mathbb{Q}[X_1^{\pm 1}, X_2^{\pm 1}]$, $\mathbb{Q}[Y_1^{\pm 1}, Y_2^{\pm 1}]$, $\mathbb{Q}[Z_1^{\pm 1},Z_2^{\pm 1}]$를 이어붙여 대수 $$\mathcal{A}_2 = \mathbb{Q}[X_1^{\pm 1}, X_2^{\pm 1}] \cap \mathbb{Q}[Y_1^{\pm 1}, Y_2^{\pm 1}] \cap \mathbb{Q}[Z_1^{\pm 1}, Z_2^{\pm 1}]$$ 를 정의하는데, 이 때 처음 두 로랑 다항식 대수 $\mathbb{Q}[X_1^{\pm 1}, X_2^{\pm 1}]$, $\mathbb{Q}[Y_1^{\pm 1}, Y_2^{\pm 1}]$는 이전과 같은 풀칠 공식으로 이어붙이고, 세 번째 로랑 다항식 대수 $\mathbb{Q}[Z_1^{\pm 1}, Z_2^{\pm 1}]$는 첫 번째 로랑 다항식 대수 $\mathbb{Q}[X_1^{\pm 1}, X_2^{\pm 1}]$와 다음의 풀칠 공식으로 이어붙인다:$$X_1 = Z_1(1+Z_2^{-1})^{-1}, \qquad X_2 = Z_2^{-1}.$$그러면 $\mathcal{A}_2$는 $X_1,X_2$에 대한 유리계수 로랑 다항식 중에서, $Y_1,Y_2$로 바꿔 썼을 때에도 로랑 다항식이 되고, $Z_1,Z_2$로 바꿔 썼을 때에도 로랑 다항식이 되는 것들이 모두 모여 이루는 대수이다.

정의로부터, $\mathcal{A}_2$가 $\mathcal{A}_1$의 부분 집합, 즉 부분 대수가 됨을 알 수 있다. 하지만 $\mathcal{A}_2$와 $\mathcal{A}_1$이 같지는 않다. 예컨대 $X_1^{-2}$은 $X_1, X_2$에 관해서도 로랑 다항식이고, $Y_1,Y_2$에 관해서 써봐도 $X_1^{-2} = Y_1^{2}$이므로 로랑 다항식이며, $Z_2,Z_2$에 관해서 써봐도 $X_1^{-2} = Z_1^{-2}(1+Z_2^{-1})^2$이므로 로랑 다항식이다. 따라서 $X_1^{-2}$는 $\mathcal{A}_2$의 원소이며, 물론 $\mathcal{A}_1$의 원소이기도 하다. 반면 $X_1^2$는 $X_1,X_2$에 관하여 로랑 다항식이고, $Y_1,Y_2$에 관하여 써봐도 $X_1^2 = Y_1^{-2}$이므로 로랑 다항식이지만, $Z_1,Z_2$에 관하여 써보면 $X_1^2 = Z_1^2 (1+Z_2^{-1})^{-2} = \frac{Z_1^2}{(1+Z_2^{-1})^2} = \frac{Z_1^2 Z_2^2}{(1+Z_2)^2}$ 이어서 로랑 다항식이 아니다. 따라서 $X_1^2$은 $\mathcal{A}_1$의 원소이기는 하지만 $\mathcal{A}_2$의 원소는 아니다.

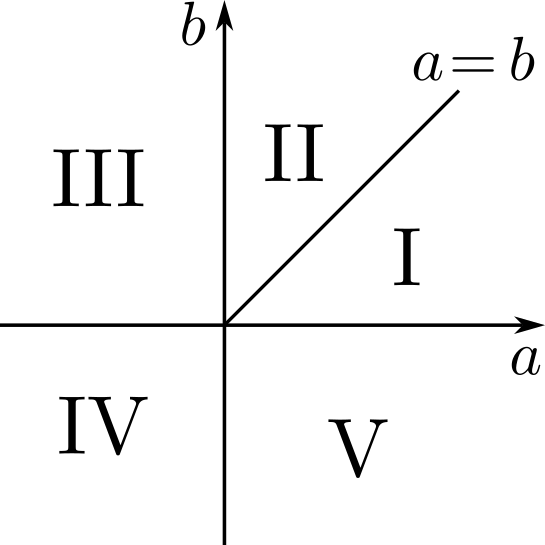
일반적으로, 조건이 더 많이 붙어 있는 $\mathcal{A}_2$의 원소들을 찾는 일이 조건이 덜 붙어 있는 $\mathcal{A}_1$의 원소들을 찾는 일보다는 더 어려울 것임을 예상할 수 있다. 그러나 특이하게도, 표준기저에 관한 문제는 $\mathcal{A}_1$보다 $\mathcal{A}_2$에 대해서 더욱 접근 가능하며, 실제로 $\mathcal{A}_2$는 표준기저라고 부를 수 있는 기저를 가짐이 알려져있다. 이 기저는 무한 개의 원소로 이루어진 집합인데, 두 정수의 순서쌍들 $(a,b)$의 집합인 $\mathbb{Z}^2$과 일대일대응을 이룬다. 정수 순서쌍 $(a,b)$에 대응하는 기저 원소를 $v_{(a,b)}$라고 하면, 이 기저 원소들은 다음 표와 같이 $(a,b)$의 조건에 따라 다섯 가지의 종류로 나뉘어 기술될 수 있다.

위의 답은 폭^Fock과 곤차로프^Goncharov가 [5], [7] 에서 증명 없이 제시하였다. 이 $\mathcal{A}_2$의 표준기저 문제는 사실 어떤 거대한 숲에 살고 있는 나무 하나라고 볼 수 있는데, 이는 다음 절에서 다룰 것이다. 약간의 맛보기를 위하여, 위의 답이 내포하고 있는 기하학적 측면을 살펴보자. 각 기저 원소를 이름짓는 정수 순서쌍들 $(a,b)$는 좌표평면 $\mathbb{R}^2$의 정수 격자점들, 즉 좌표 값들이 모두 정수인 점들로 이해할 수 있다. 위의 표에 나오는 정수 격자점들의 다섯 가지의 종류는 그림 1에서와 같이 좌표 평면을 나누는 다섯 개의 영역으로 이해할 수 있다.

클러스터 다양체

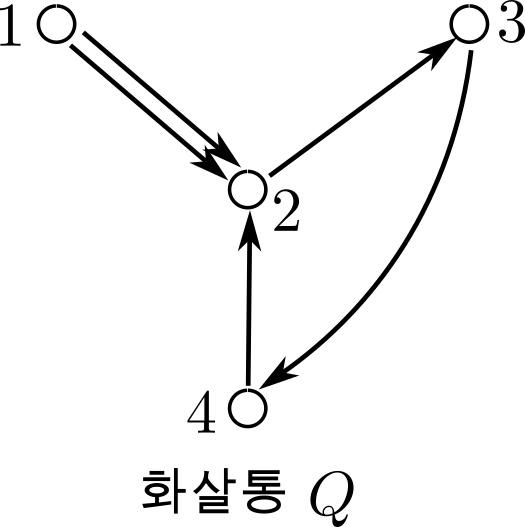
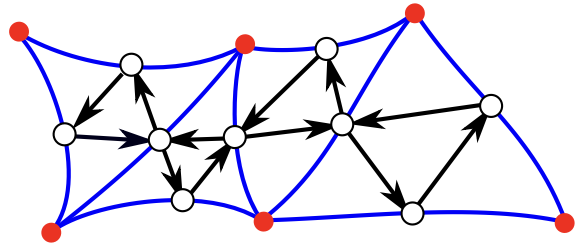
이전 절에서 언급된 숲이란 2000년대 초반부터 연구되어 온 클러스터 다양체^{cluster variety} 이론이다([7] 참조). 클러스터 다양체를 정의하려면 유한 개의 점들과 그들을 잇는 유한 개의 화살표로 이루어진 그래프, 즉 화살통^quiver $Q$ 하나를 골라야 한다. 우리는 화살통을 그림 2와 같이 그림으로 나타내고 이해하곤 하지만, 우리의 논의에서는 꼭 화살표들이 곧은 선분일 필요는 없고, 각 화살표에 대해서 중요한 정보는 어느 점에서 시작해서 어느 점까지 가느냐이다. 즉, 점들을 $1,2,\ldots,N$과 같이 이름 붙이면, 각 $i,j \in \{1,\ldots,N\}$에 대해서 점 $i$에서 시작하여 점 $j$로 끝나는 화살표의 개수인 $a_{ij}$들만 알고 있으면 된다는 것이다. 나아서, 클러스터 다양체 이론에서는 화살표 개수의 부호-총합^{signed net sum}인$$\varepsilon_{ij} = a_{ij} – a_{ji}$$만이 유의미하게 필요한 정보이다. 즉 화살통 $Q$를 그림 2와 같이 그림으로 다루어도 되지만, 위의 숫자들 $\varepsilon_{ij}$만 모아서 크기가 $N \times N$ 인 정사각행렬로 만들어 이 행렬만 다루어도 된다.

클러스터 다양체의 정의 중 하나는, 어떤 고정된 자연수 $N$에 대해서, $N$변수 로랑 다항식 대수 $\mathbb{Q}[X_1^{\pm 1}, \ldots, X_N^{\pm 1}]$ 여러 개를 모종의 풀칠 공식으로 이어 붙여서 만들어지는 대수기하적 대상이다. 첫 번째 연재글 [1] 에서 대략 언급되었듯이, 방금의 문장은 함수들의 모여 이루는 대수 입장에서의 기술이고, 기하학적 입장에서는 $N$차원 ‘토러스^{torus, 원환면}’ 여러 개를 이어붙인다고 이해하면 된다. 이때 풀칠하는 각 로랑 다항식 대수 혹은 토러스에 추가적인 정보로서 화살통 하나씩을 부여하며, 화살통의 각 점들은 로랑 다항식 대수의 생성자 하나, 즉 좌표함수 하나와 대응된다고 생각한다. 예컨대 대수 $\mathbb{Q}[X_1^{\pm 1}, \ldots, X_N^{\pm 1}]$에 화살통 $Q$가 부여되었을 때, 화살통 $Q$의 점들이 $1,2,\ldots,N$로 이름붙여져 있고, $i$번째 점이 $X_i$에 대응된다고 생각하면 된다.

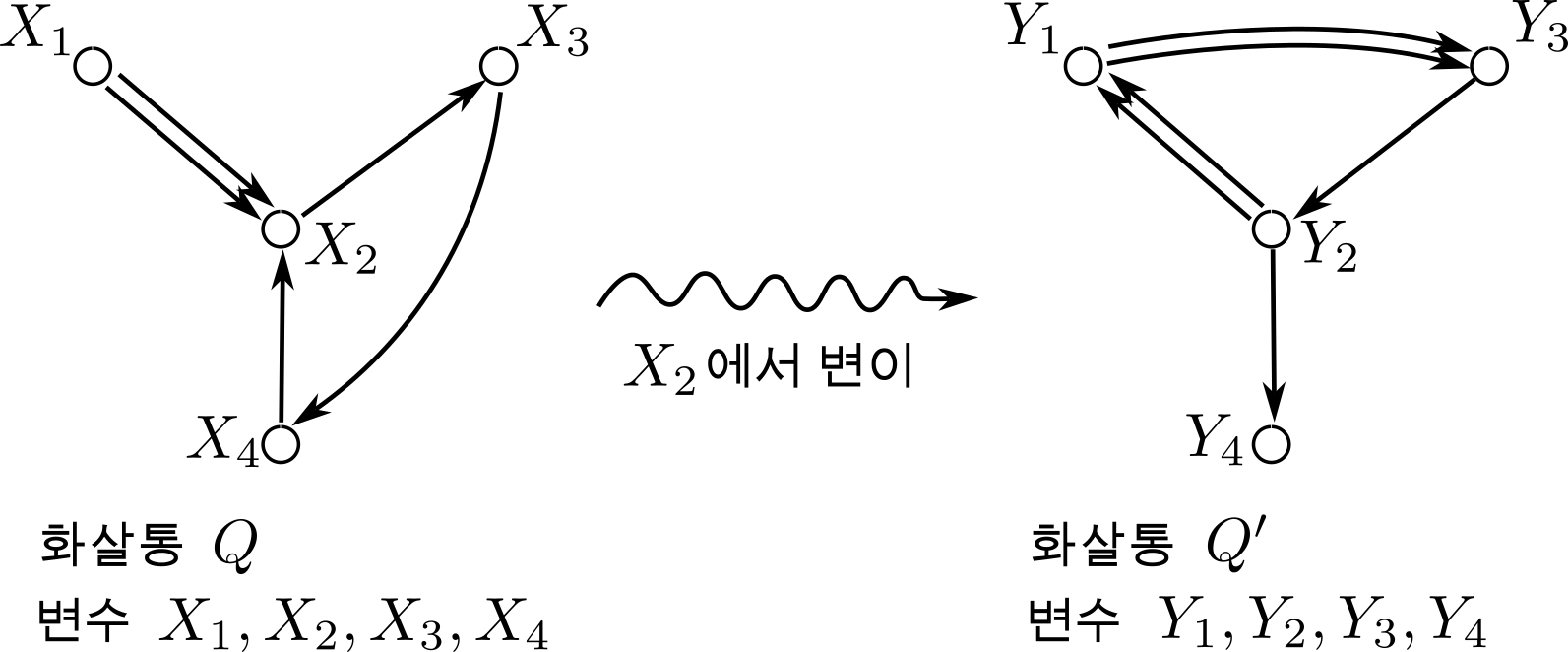
이렇게 로랑 다항식 대수와 그에 부여된 화살통 하나의 쌍을 클러스터 다양체의 씨앗^seed라고 부른다. 씨앗 하나에 대해, 화살통의 점 하나 $k$(여기에는 변수 $X_k$가 붙어있다)를 골라서 씨앗의 그 점을 중심으로 한 ‘근방’을 변이^mutate시켜서 새로운 씨앗을 생성하는 공식이 있다. 원래의 씨앗의 로랑 다항식 대수를 $\mathbb{Q}[X_1^{\pm 1},\ldots,X_N^{\pm 1}]$, 그 화살통을 $Q$라고 하고, $k$번째 점(혹은 변수 $X_k$)에 대하여 변이를 수행하여 얻어지는 씨앗의 로랑 다항식 대수를 $\mathbb{Q}[Y_1^{\pm 1},\ldots, Y_N^{\pm 1}]$, 그 화살통 대수를 $Q’$라고 하자 (변수들의 이름은 정하기 나름인데, 편의상 $X$와 $Y$를 사용하였다). 그러면 변이된 화살통 $Q’$는 화살통 $Q$에다가 다음의 조합론적인 작업을 수행하여 얻어진다:

이 화살통 변이 공식은 누구나 이해할 수 있고 수행하기는 쉽지만(그림 3 예시 참조), 처음 보면 왜 이런 이상한 공식을 생각해야 하는지 의문이 들 수 있다. 이러한 의문은 변이 전과 후의 두 로랑 다항식 대수를 관계지어주는 변수 변이 공식에 대해서도 가질 수 있다. 이를 풀칠 공식으로 이해할 수 있으며, 다음과 같이 화살통 $Q$의 화살표 개수 부호-총합 $\varepsilon_{ij}$들을 사용해 기술할 수 있다:$$Y_k = X_k^{-1}, \qquad Y_i = X_i( 1+ X_k^{ {\rm sign}(\varepsilon_{ki})})^{\varepsilon_{ki}} \quad (\mbox{모든 $i\neq k$에 대해}).$$여기서 ${\rm sign}(\varepsilon_{ki})$는 $\varepsilon_{ki}$의 부호에 따라 $1,0,-1$값을 가지는 것으로 정의한다. 그림 3에 제시된 예의 경우, $k=2$이며 변수 변이 공식이 다음과 같이 주어진다:
$$Y_2 = X_2^{-1}, \quad Y_1 = X_1( 1+ X_2^{-1})^{-2},\quad Y_3 = X_3( 1+ X_2),\quad Y_4 = X_4( 1+ X_2^{-1})^{-1}.$$
예컨대 $i=1$에 대해 $\varepsilon_{21} = -2$이므로, $Y_1 = X_1(1+X_2^{-1})^{-2}$ 이다.

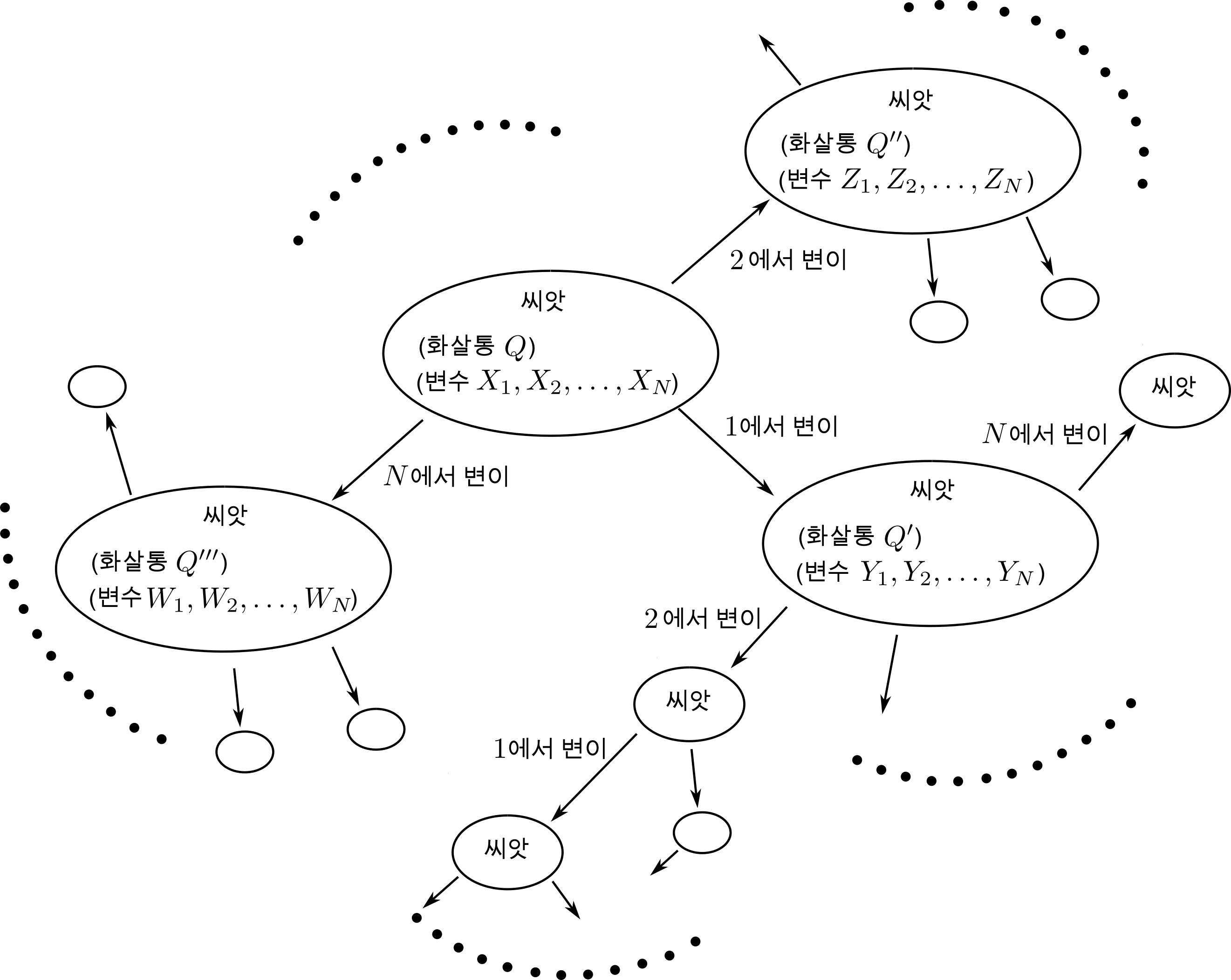
공식의 의미에 대해서 생각하는 대신 일단 공식은 공식으로 받아들이고 좀 더 나아가보자. 씨앗 한 개로부터 시작하면, 씨앗의 화살통의 각 점마다 그 점에 대해 이 씨앗을 변이시켜 $N$개의 새로운 씨앗을 생성할 수 있고, 원래의 씨앗의 로랑 다항식 대수와 각 새로운 씨앗의 로랑 다항식 대수를 이어붙이는 풀칠 공식을 얻는다. 이젠 새로운 씨앗들 각각에 대해서도 변이들을 또 적용하여 더 많은 씨앗을 생성하고, 이 작업을 끝없이 반복한다(그림 4). 일반적으로는 무한 개의 씨앗들을 생성하게 되고, 각 씨앗의 로랑 다항식 대수들을 서로 어떻게 이어 붙일 지에 대한 공식들도 얻게 된다(그림 4에서 볼 수 있듯이, 이것들을 잘 다루려면 효율적인 표기법을 개발해야 할 필요성을 느끼게 된다). 이렇게 한 개의 씨앗에서 시작하여 얻어지는 모든 씨앗들의 로랑 다항식 대수를 전부 이어붙여 얻어지는 대상을 클러스터 다양체라고 부른다. 이 대상은 처음 씨앗이 무엇인지에 따라 결정되고, 처음 씨앗이 가진 유의미한 정보는 사실 화살통 뿐이므로, 임의의 화살통 $Q$ 하나를 고를 때마다 그에 대응하는 클러스터 다양체 하나를 만들 수 있다고 보면 된다. 우리는 편의상 특정한 한 종류의 변수 변이 공식을 풀칠 공식으로 사용했는데, 이 경우는 클러스터 X-다양체 $\mathscr{X}_{|Q|}$를 얻게 된다([엑스 큐 바]로 읽으면 된다). 참고로, 이와는 다른 종류의 변수 변이 공식들도 있고, 그 중 어떤 한 종류를 대신 사용하면 대수적인 성향의 연구자들이 선호하는 클러스터 A-다양체를 얻는다. 아래첨자를 $Q$가 아니고 $|Q|$로 표기한 이유는, $Q$ 대신 $Q$에다가 화살통 변이 공식을 여러 번 적용하여 얻어지는 아무 화살통 $Q’$를 사용해도 같은 클러스터 다양체를 얻는다는 사실을 나타내기 위함이다.

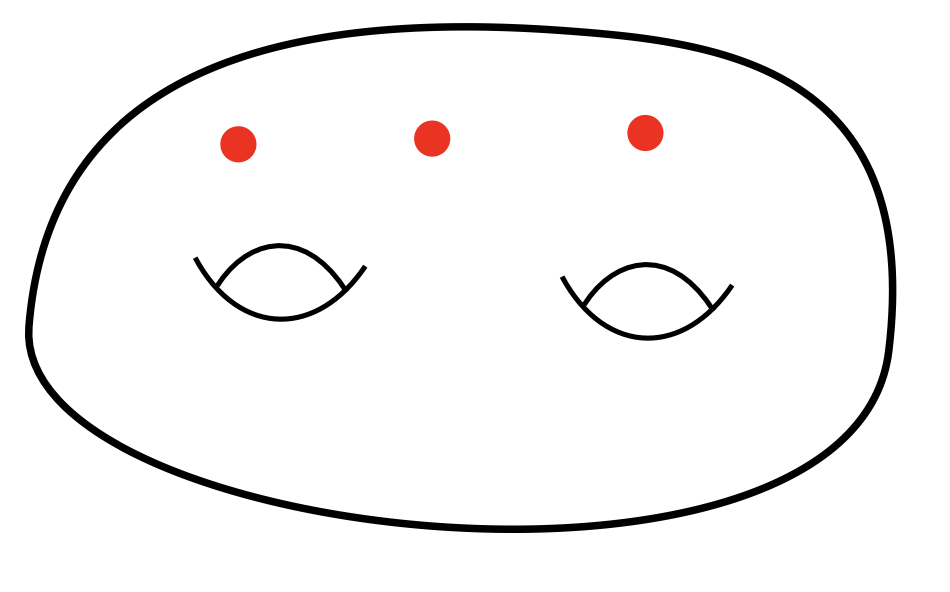
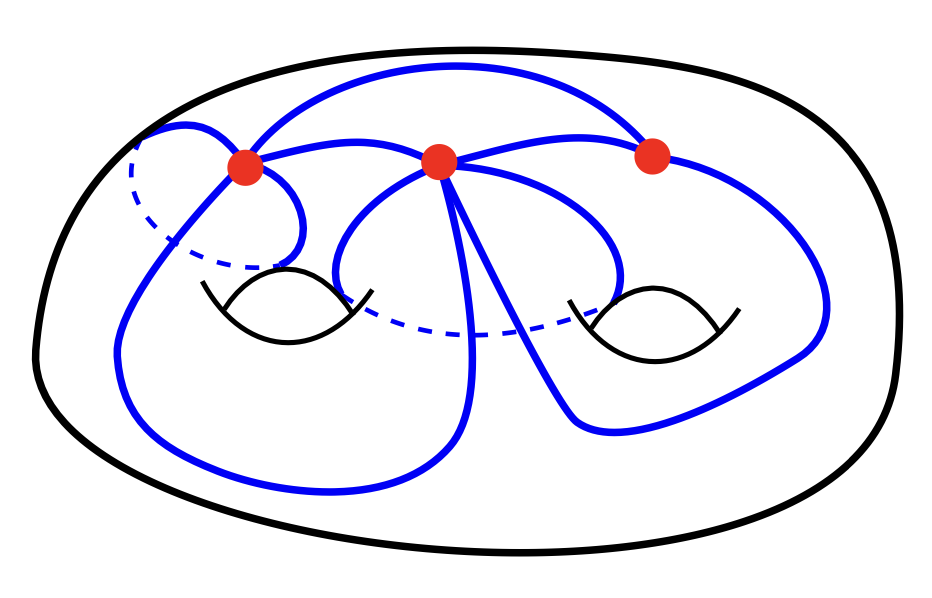
놀라운 점은, 일견 상당히 작위적으로 보이는 공식들을 사용하여 건설된 클러스터 다양체가 수학의 곳곳에서 많이 발견되었다는 점이다. 즉, 위의 공식들로 설명할 수 있는 중요한 수학적 대상이 많다는 것이다. 따라서 클러스터 다양체 일반에 관한 이론을 연구하여 어떤 명제를 얻으면, 많은 중요한 예시들에 적용할 수 있게 된다. 참고로 필자가 가장 오랜 기간 연구한 예시는, 닫힌 유향곡면에서 구멍 여러 개를 뚫어서 얻는 구멍난 곡면^{punctured surface} $S$에 대하여(그림 5), 구멍들을 연결하는 곡선을 여러 개 그어서 $S$를 삼각형들로 분할하고(그림 6; 사실은 더 많은 곡선이 필요하지만 몇 개만 그렸다), 각 삼각형마다 그림 7에서와 같이 주어진 삼각형 모양 화살통들을 모두 이어붙여 얻는 화살통 $Q$의 경우이다. 이 경우 클러스터 다양체 $\mathscr{X}_{|Q|}$가 구멍난 곡면 $S$ 위의 어떤 자연스러운 기하구조들의 모임인 타이히뮐러 공간^{Teichmüller space}과 밀접한 관련이 있어서, 클러스터 다양체에 관한 명제와 문제들을 2차원 기하학과 위상수학으로 해석하고 접근할 수 있게 되고 또한 그 반대 방향으로의 영감도 얻을 수 있어서 매우 흥미롭다([6]).

한편, 앞 절에서 나온 대수 $\mathcal{A}_2$에 관한 문제는 점의 개수가 $N=2$이며 화살표가 하나만 있는 화살통 $\circ \hspace{-1mm} \to\hspace{-1mm} \circ$ 에 대응하는 클러스터 X-다양체에 관한 문제인 것으로 이해할 수 있다. 다만 앞 절에서는 로랑 다항식 대수 세 개만 사용하였음에도 이를 무한 개의 로랑 다항식 대수를 필요로 하는 클러스터 X-다양체의 관점에서 이해할 수 있는 이유는, 클러스터 다양체의 이론에서 정립된 어떤 강력한 정리를 필자가 몰래 사용하였기 때문이다! 반면 $\mathcal{A}_1$에 관한 문제는 클러스터 X-다양체의 틀에서 이해할 수 있을지 확실치 않다.

그러면 우리가 $\mathcal{A}_2$에 관하여 물었던 문제는 일반적인 클러스터 X-다양체에 대한 어떤 문제의 예시로 볼 수 있는가? 화살통 $Q$로부터 건설한 클러스터 X-다양체 $\mathscr{X}_{|Q|}$를 생각해보자. 이것은 많은 씨앗들로 구성되어 있으며, 각 씨앗은 로랑 다항식 대수 하나와 화살통 하나로 이루어져있다. 이 로랑 다항식 대수들은 서로 풀칠되어 있어서, 이 풀칠 공식을 이용하면 하나의 로랑 다항식 대수의 원소를 다른 로랑 다항식 대수의 생성자 변수들에 대하여 기술할 수 있다. 그런데 우리가 앞 절 $\mathcal{A}_2$의 예시에서 봤듯이, 한 씨앗에서 로랑 다항식 대수의 원소였다고 해도, 다른 씨앗의 변수로 나타내보면 유리식이기는 해도 꼭 로랑 다항식이지는 않을 수도 있다. $\mathcal{A}_2$가 세 개의 씨앗 모두에서 로랑 다항식인 원소들의 모임으로 정의되었듯이, 우리는 클러스터 X-다양체 $\mathscr{X}_{|Q|}$에 대해, 이를 구성하는 모든 씨앗에서 로랑 다항식인 원소들의 모임을 생각할 수 있다. 이 모임은 대수를 이루며 $\mathcal{O}(\mathscr{X}_{|Q|})$로 표기한다([오 엑스 큐 바]와 같이 읽으면 된다). 우리의 정의를 대략적으로 다음과 같이 써볼 수 있다:$$\mathcal{O}(\mathscr{X}_{|Q|}) = \bigcap_{\mbox{씨앗들}} (\mbox{각 씨앗을 이루는 로랑 다항식 대수}).$$이 대수 $\mathcal{O}(\mathscr{X}_{|Q|})$의 원소를 클러스터 X-다양체 $\mathscr{X}_{|Q|}$ 위의 좋은 함수로 이해할 수 있는데, 대역적으로 정칙^{globally regular}인 함수, 혹은 보편 로랑^{universally Laurent} 함수라고 부르곤 한다. 다음 추측은 클러스터 다양체 이론 전체를 관통하는 가장 중요한 연구 줄기들 중 하나를 이룬다:

추측. 임의의 화살통 $Q$에 대해, 보편 로랑 함수들의 대수 $\mathcal{O}(\mathscr{X}_{|Q|})$는 표준기저를 갖는다.

사실 이 추측은 우리가 엄밀하게 정의하지는 않은 단어인 ‘표준기저’만을 사용해서 위와 같이 다소 무책임하게 쓰여있는 것이 아니라, 이 기저가 가져야 하는 대수적이거나 기하적인 성질들이 훨씬 정교하게 수학적으로 기술되어 있으며 (기하적인 성질의 일면은 앞 절 그림 1과 같은 느낌이다), 위의 버전 외에도 다른 버전들이 존재하고, 이를 통칭 폭-곤차로프 추측들^{Fock-Goncharov conjectures}라고 부른다([7]). 앞 절에서 제시한 결과는 화살통 $Q$가 $\circ \hspace{-1mm} \to \hspace{-1mm} \circ$인 경우 이 추측(의 한 버전)에 대한 답으로 알려져 있다.

이 추측이 처음 등장한 2000년대에는, 많은 수학자들이 표준기저를 얻어내고 이해하고자 했던 특정한 예시들, 즉 리 대수, 양자군, 그리고 그 표현들의 이론에 관한 예시들에서 이미 발견되었거나 발견하고자 했던 현상을 더욱 깊이 이해하게 하고 또한 매우 크게 확장하는 추측이라는 의미를 지니고 있었다.

접근법의 다양성

폭-곤차로프 추측이 처음 발표된 후 10여년 정도의 기간 동안 많은 학자들이 클러스터 다양체 이론을 연구했으나 이 표준기저 문제에 대한 진전은 몇 가지의 특정한 족에 속하는 화살통 $Q$들의 경우에 대해서만 이루어졌다. 이윽고 그로스^Gross, 해킹^Hacking, 킬^Keel, 콘세비치^Kontsevich는 다음의 획기적인 결과를 얻었고, 이를 2018년에 출판하였다.

정리 ([8]). 어떤 특정한 조합론적 조건을 만족하는 모든 화살통 $Q$에 대해서 $\mathcal{O}(\mathscr{X}_{|Q|})$는 표준기저를 갖는다.

이 정리에서 말하는 조합론적 조건은 몇 가지 다른 방식으로 설명될 수 있다. 그 중 하나는 ‘최대 녹색 수열의 존재성^{existence of a maximal green sequence}’인데, 이 글에서는 이 조건이 정확히 무엇인지 구체적으로 설명하지는 않겠다. 정의 자체는 어렵지 않지만, 임의의 화살통을 가져왔을 때 그 화살통이 이 조건을 만족하는지 체크하는 일은 간단하지 않은 것으로 알고 있다. 언뜻 생각하면 위의 정리가 모든 화살통에 대한 정리가 아니고 특정 조건을 만족하는 화살통에 대해서만 다뤘으므로 제한적인 것 같지만, 지금까지 연구자들이 관심있어 해온 거의 모든 화살통이 이 조건을 만족하는 것으로 밝혀졌거나 믿어지는 것으로 필자는 알고 있고, 오히려 이 조건을 만족하는 화살통들에 대해서만 폭-곤차로프 추측을 고려하는 것이 맞는 방향이라는 견해도 있다. 여하간 위의 그로스-해킹-킬-콘세비치의 정리가 폭-곤차로프 추측을 어떤 의미에서는 거의 모든 경우에 대하여 해결했다고 여길 수 있어서, 이것만으로 대단히 훌륭한 결과라는 것을 알 수 있다.

그런데 이 결과의 더욱 흥미로운 점은 그 해결 방법이 기존의 클러스터 다양체 이론이 아니라 전혀 다른 이론을 사용했다는 것이다. 이것은 대수기하학에 속한다고 볼 수 있는 ‘로그 칼라비-야우 다양체의 거울대칭 이론’이다. 이론물리학에서의 관찰과 추측에서 출발한 거울대칭^{mirror symmetry} 이론은 수학에서 사교기하학^{symplectic geometry}와 복소기하학^{complex geometry} 간의 대응으로 이해되어 발전되었으며(유필상 교수의 호라이즌 글[9] 참조), 그간 연구되어 온 몇 가지의 주요 방향 중 하나가 대수기하학과 조합론적인 언어로 쓰여졌고, 이것의 다소 사소한 따름정리로서 위의 정리가 얻어졌다. 킬^Keel은 자신의 강연 중 하나에서 그들이 제시한 기저의 건설 방법을 이해하는 누구라도 그 건설이 표준적임을 인정할 것이라고 말했는데, 바로 이 점이 표준성의 정의로 볼 수 있다는 재미있는 언급을 하였고, 이는 필자가 본 연재 시리즈를 시작한 계기 중 하나가 되었다([1] 참조). 킬의 견해에 동의하는 사람이라면, 결과론적으로 그로스-해킹-킬-콘세비치의 표준기저의 건설은 대수기하학의 표준적인 개념과 건설들로 이루어져있다고 평가할 것이다.

하지만 이 건설이 지난 연재글([2],[3],[4])에서 다룬 것과 비슷한 범주화의 방식으로 이루어졌다고 보기는 어렵다. 요컨대, 어떤 대수의 표준기저의 존재나 건설을 얻어내는 데에는 보통 그 대수 자체의 대수적 구조 뿐만 아니라 추가적인 구조 혹은 정보가 필요하긴 하지만, 그러한 추가적인 구조를 통해 표준기저를 얻어내는 방식은 꼭 범주화만 있는 것은 아니라는 것이다. 그로스-해킹-킬-콘세비치의 방법론은 우리가 살펴봤던 범주화 방법론과는 질적으로 다른 새로운 것이며, 어떤 대수의 경우는 모종의 기하학이나 다른 분야의 표준적인 건설이 버무려져 있는 또 다른 방법들도 있을 것이다.

경쟁과 상생

어떤 화살통들 $Q$에 대해서는 그로스-해킹-킬-콘세비치의 방법론과 지난 연재글들에서 다룬 것과 비슷한 범주화의 방식 모두가 적용될 수 있다. 즉 이러한 $Q$에 대해서는 많은 연구자들이 표준기저의 건설이라고 인정할 만큼 충분히 표준적인 건설법이 하나의 대수에 대해 적어도 두 가지가 존재한다는 것이다. 만약 두 가지의 서로 다른 표준적인 건설법으로부터 같은 기저가 도출된다면, 우리는 이 기저의 표준성에 대하여 더욱 굳건한 믿음을 가지게 될 것이다. 그런데 문제는 이 두 건설법으로부터 얻어지는 기저가 서로 다를 때이며, 실제로 그런 경우들이 연구된 바 있다.

이럴 때에는 하나의 대수가 표준기저라고 부를 수 있는 기저를 적어도 두 개 가지게 된다. 만약 ‘표준기저’라는 개념을 ‘공동 1등 없이 단독 1등으로 훌륭한 기저’와 같이 여기자고 결심한다면([1] 참조), 우리는 둘 중 어느 것이 더 표준적인지 따져봐야 할 것이다. 그런데 꼭 이렇게 1등과 2등을 가려야만 하는가? 우리는 왜 표준기저를 찾으려고 했던가? 그것은 주어진 벡터공간이나 대수의 수많은 가능한 기저들 중 되도록이면 인위적인 선택이 없이 하늘에서 뚝 떨어진 자연스러운 기저, 훌륭한 기저, 가능하면 가장 훌륭한 기저를 가지길 원했기 때문인 것으로 필자는 생각한다. 만약 ‘어디에 내놔도 손색없이 훌륭한 표준성’을 가진 기저가 두 개라면? 이럴 때는 그냥 두 가지 모두를 끌어안고, “이 벡터공간 혹은 대수는 보는 관점에 따라 표준기저를 여러 종류 찾아낼 수 있는 것을 보니 팔색조같이 다채로운 매력을 지닌 녀석이로군”이라고 받아들일 수도 있지 않을까 한다.

이렇게 다소 농담이 섞인 정신승리는 하지 않기로 하더라도, 사실 수학 연구자로서는 이런 경우가 더욱 흥미로운 연구 거리가 될 수 있다. 일반적으로 벡터공간의 기저가 있을 때, 벡터공간의 임의의 원소에 대하여 그 원소를 기저에 대해서 표현할 수 있다. 즉 이 원소를 기저의 원소들에 상수 계수들을 곱하여 더한 형태로, 즉 선형 결합으로 나타낼 수 있다. 충분히 표준적인 기저 두 가지가 있을 때, 우리는 한 쪽 기저의 각 원소가 다른 쪽 기저에 대해 어떻게 표현되는지, 즉 다른 쪽 기저의 원소들의 선형 결합으로 어떻게 표현되는지, 즉 기저 변환 공식을 연구해볼 수 있다. 이 선형 결합 표현들은 두 표준기저들을 관계지어주는 공식이므로, 거기에 나타나는 계수들이 흥미로운 성질을 가질 가능성이 높다. 이 계수들은 처음 시작한 벡터공간에 상수곱 구조를 주는 체의 원소인데, 예컨대 유리수 혹은 복소수 등이다. 기저 변환 공식에서 나타나는 계수들이 흥미로운 성질을 가지는 대표적인 경우는 그 계수들이 신기하게도 모두 정수일 때, 나아가서는 모두 음이 아닌 정수일 때이다. 이런 때에는 음이 아닌 정수인 이 계수들이 어떤 수학적 대상들을 세는 개수로 주어지거나, 어떤 벡터공간 혹은 기하적 공간의 차원으로 주어질 것이라는 기대를 할 수 있고, 실제로 그렇다는 것을 알아내는 일은 훌륭한 연구 주제이다.

한편, 수학자들이 늘 이상만 좇는 것은 아니다. 우리가 자동차를 구입하고자 할 때, 만약 꼭 성능이 가장 좋은 차를 사야 한다는 원칙을 세운다면, 그리고 그 차의 가격이 너무 비싸다면, 우리는 그 차를 사기 위해 다른 많은 것을 포기해야 할 수도 있고, 살 수 있을 때까지 시간이 너무 많이 걸릴 수도 있으며, 어떤 경우는 예컨대 너무 복잡한 기능이 탑재되어 있어서 실제 사용하기가 쉽지 않을 수도 있다. 따라서 실질적으로는 우리 각자의 현재 경제적 능력을 고려하여 지금으로부터 적당한 시간 내에 살 수 있고 적당한 성능을 가진 차를 구입하는 것이 합리적일 수도 있다. 자동차를 한 번도 타보지 않은 사람이라면, 이렇게 현실적 상황을 고려하여 산 차를 타면서 최고의 성능을 가진 차에 대한 이해에 더욱 가까워질 수도 있다.

이와 비슷하게, 벡터공간이나 대수의 기저들 중에 어떤 면에서는 수학적으로 가장 훌륭한 성질을 지닌 표준기저만을 찾고자 할 수도 있지만, 그 표준기저가 찾기에 혹은 건설하기에 너무 어렵고 복잡할 수도 있고, 실제 ‘사용’하기에 너무 어려울 수도 있다. 심지어는 존재성을 증명할 수는 있지만 내 손에 전혀 잡을 수가 없어서 그 어떤 계산도 하기가 매우 어렵거나 불가능한 경우가 있다. 참고로 그로스-해킹-킬-콘세비치의 표준기저가 대부분의 화살통 $Q$의 경우 그러하다. 이럴 때에는 혹 충분히 표준적이지 않거나 또는 표준적이라고 아직 증명되지는 않았다고 하더라도, 이해하기 쉽고 건설하기 쉬우며 사용하기 쉬운 어떤 기저를 만약 찾을 수 있다면 그런 기저를 찾고 사용하는 것이 표준기저의 탐구 만큼이나 의미있는 일일 수 있다. 특히, 수학자들간의 수학적 아이디어의 소통이 인간이 수학을 한다는 것의 본질 중 하나라는 써스턴^{W. P. Thurston}의 견해를 수용한다면([10]), 이해하고 사용하기 쉬운 기저가 수학의 발전에 있어서 표준기저가 미처 행하지 못할 수도 있는 중요한 역할을 한다고 받아들일 수도 있을 것이다.

표준기저에 관한 폭-곤차로프 추측의 주창자 중 하나인 곤차로프^Goncharov는 최근 필자와의 대화에서 이와 같은 기저, 좀 더 정확히는 그러한 건설을 교과서적 건설^{textbook construction}이라고 표현하였다. 이를 빌려서 ‘교과서적 기저’라는 개념을 생각해볼 수 있을 것이다. 나아가서, 만약 하나의 벡터공간 혹은 대수가 표준기저도 가지고 있고 이와는 다른 교과서적 기저도 가지고 있다면, 표준기저와 교과서적 기저 간의 관계, 즉 그들 간의 기저 변환 공식을 연구해볼 수 있을 것이다. 이 기저 변환 공식을 잘 기술할 수 있다면, 이를 비교적 이해하기 쉬운 교과서적 기저를 통하여 이해하기 쉽지 않은 표준기저에 접근하는 방편으로 여길 수 있겠다. 물론 이 기저 변환 공식의 계수들이 명확히 기술가능할 뿐 아니라 특별한 성질을 가지고 있다면 더욱 흥미로울 것이다.

예를 들어보자. 지난 연재글 [4]에서는 일변수 유리계수 다항식 대수 $\mathbb{Q}[x]$의 표준기저 하나 $\{G_0(x), G_1(x), G_2(x), \ldots\}$를 범주화 방법론을 통해 얻었던 바 있다. 답만 언뜻 보면 표준성이 피부에 와닿지는 않을 수도 있는 이 기저는 다음과 같이 주어진다:$$G_0(x) = 1, \quad G_1(x) = x, \quad G_2(x) = x^2 – 1, \quad G_3(x) = x^3 – 2x, \quad G_4(x) = x^4 – 3x^2 + 1, \quad \cdots.$$한편 우리는 $\mathbb{Q}[x]$의 훨씬 이해하기 쉬운 기저 $\{F_0(x), F_1(x), F_2(x),\ldots\}$, 즉 단항식들로 이루어진 기저를 이미 알고 있었다:$$F_0(x) = 1, \quad F_1(x) = x, \quad F_2(x) = x^2, \quad F_3(x) = x^3, \quad F_4(x) = x^4, \quad \cdots.$$

필자는 지난 연재글들을 통해서 $\{G_0(x),G_1(x),\ldots\}$의 표준성을 주장하기 위하여 이 단항식 기저 $\{F_0(x),F_1(x),\ldots\}$의 표준성을 열심히 깎아내리려는 시도를 해 왔다. 물론 이는 필자가 이 단항식 기저에 특별한 악감정이 있어서라기보다는 글의 논의 전개를 위하여 그렇게 한 것이지만, 어쨌든 이 기조를 이어서 우리는 이 단항식 기저가 별로 표준적이지는 않다고 여겨보자. 표준성은 조금 결여되어 있을 수 있지만, 이해하기 쉽고 사용하기 쉽다는 것은 누구나 동의할 수 있을 것이며, 따라서 이 기저를 교과서적 기저라고 받아들일 수도 있을 것이다. 교과서적 기저인 이 단항식 기저와 표준기저인 $\{G_0(x),G_1(x),\ldots\}$ 간의 기저 변환 공식을 살펴보자. 한 방향만 살펴볼 텐데, 단항식 기저의 각 원소를 표준기저로 표현하면 다음과 같다:$F_0(x) = G_0(x)$, $F_1(x) = G_1(x)$,$$F_2(x) = G_2(x) + G_0(x), \quad F_3(x) = G_3(x) + 2 G_1(x), \quad F_4(x) = G_4(x) + 3 G_2(x) + 2 G_0(x), \quad \cdots.$$

실제로, 각 $F_n(x)$ 를 $\{G_0(x),G_1(x),\ldots\}$의 선형 결합으로 표현해보면 모든 계수가 음이 아닌 정수라는 사실을 증명할 수 있다! 증명 자체는 지난 연재글 [4] 에 나온 $G_n(x)$들 간의 귀납적 점화식을 사용하면 초보적인 방법으로 증명할 수는 있지만, 이 계수들이 가진 더 깊은 의미를 알아내는 편이 좀 더 흥미로울 것이다. 증명과 의미를 찾는 일은 독자들에게 남긴다.

위와 비슷한 일이 표현론^{representation theory}라는 분야에서 있었다. 지난 글에서 얻은 기저 $\{G_0(x),G_1(x),\ldots\}$는 리 대수^{Lie algebra}라고 불리는 어떤 대수적 대상의 ‘표현^{representation}’ 혹은 ‘모듈^module’들의 범주에서 더 작은 표현으로 쪼개지지 않는 단순 표현 혹은 단순 모듈^{simple module}들로부터 얻어내었으며, 이는 표현론에서 널리 받아들여지는 표준적인 건설이다. 리 대수와 표현에 대해서는 지난 연재글 [3]이나 [11], [12] 를 참조하면 좋고, 모듈은 여기서는 표현과 같은 말로 받아들여도 된다. 그런데 리 대수의 표현론에서 단순 모듈만큼 표준적인 개념은 아니지만 교과서적 건설로 여겨지는 것으로 베르마 모듈^{Verma module}이 있다([12]). 단순 모듈들 대신 베르마 모듈들을 사용해도 지난 글에서처럼 어떤 대수의 기저를 하나 얻을 수 있는데, 단순 모듈들로부터 오는 기저와 베르마 모듈들로부터 오는 기저를 비교하는 기저 변환 공식을 연구해볼 수 있다. 이 변환 공식의 계수들의 이해에 관한 카즈단-루스틱 추측^{Kazhdan-Lusztig conjecture}는 표현론 발전의 역사에서 가장 중요한 추측 중 하나로 받아들여진다.

맺음말

필자는 수학에서 한 문제의 가치는 꼭 문제 자체나 문제에 대한 최종 답에만 있는 것이 아니라, 답을 구하는 과정에서 어떠한 풍부한 수학적 이야기가 있었는가에도 달려있다고 생각한다. 이러한 가치는 종종 오직 사후적으로만 깨달을 수 있다. 예컨대 페르마의 마지막 정리가 훌륭한 문제라고 인정받는 이유는, 그 문제 자체가 애초부터 정말 너무 중요한 문제였다기 보다는, 그 문제의 해결을 위하여 수학의 매우 깊은 새로운 분야와 방법론들이 새로이 발전되었기 때문이라고 본다.

필자는 벡터공간이나 대수의 표준기저 문제도 비슷한 관점으로 평가할 수 있다고 생각한다. 즉, 표준기저라는 개념이 그 자체로 근본적으로 중요하다기보다는, 많은 흥미로운 경우에 표준기저 문제의 해결에 다양하고 풍부한 여러 수학이 쓰였고 서로 상호작용한다는 것을 발견했기 때문에 훌륭한 연구 주제라고 볼 수 있다는 것이다. 여행의 목적지도 중요할 수 있지만, 여행 자체가 의미있을 수 있는 것이고¹, 때로는 무언가를 찾아서 전 세계를 헤매다가 아무 것도 찾지 못하고 제 자리로 돌아와서 내가 찾던 것이 내가 원래 있던 자리에 있다는 것을 깨닫기만 했을 지라도, 그 깨달음은 내가 그것을 찾아 전 세계를 찾아 헤맸기 때문에 얻을 수 있었던 것일지도 모른다².

언젠가 필자가 직접 찾았거나 앞으로 찾아낼 아름다운 표준기저나 훌륭한 교과서적 기저를, 그리고 그것들을 찾는 여정에서 만난 흥미진진한 이야기들을 호라이즌에서 소개하게 되기를 기대한다.