우리가 살고 있는 세계는 수많은 정보로 채워져 있다. 수많은 서적들, 베토벤의 교향곡, 인터넷을 타고 흘러 다니는 엄청난 양의 사진과 동영상들, 생물체의 모든 특징이 나열되어 있는 염색체, 생물체 내부나 생물체 간의 화학적인 신호 전달, 지구와 달의 상호 작용, 심지어 내 통장의 잔고까지 이 세상 어디에도 정보가 아닌 것이 없어 보인다. 살아간다는 것, 변화가 있다는 것은 이렇게 인위적이거나 자연적인 정보의 전달 현상이라고 볼 수 있다. 정보 자체가 물리량인가에 대해서는 여러 의견이 있을 수 있겠지만, 본 글에서는 정보에 물리적인 측면이 있고 우리가 매일 이것을 사용하며 심지어 의도적으로 변형시켜 머지않은 미래에 지금까지 우리가 할 수 없었던 일을 할 수 있게 될 것이라는 이야기를 하고자 한다.
우리 눈으로 보고 감각적으로 느낄 수 있는 세계를 거시계라고 한다. 크기 단위로 생각해보면 마이크로미터 이상을 거시계라고 볼 수 있다. 이러한 거시계는 뉴턴의 고전역학으로 잘 기술된다. 하지만 더 작은 미시계로 들어가면, 특히 원자나 분자 등 나노미터 이하 크기의 시스템에서는 더 이상 뉴턴의 고전역학으로는 설명할 수 없는 현상들이 지배적으로 나타나게 된다. 이러한 현상들을 양자현상이라고 부르고 그 현상을 기술하는 확률론적인 방법을 양자역학이라고 한다. 양자 얽힘quantum entanglement, 양자 터널링quantum tunneling, 양자 중첩quantum superposition으로 대표되는, 고전 역학으로는 설명할 수 없는 양자현상들, 즉 정보로 해석될 수 있는 입자들 간의 특수한 상관관계는 놀랍게도 생명체가 생명을 유지하는데 이용될 수 있다. 또한 현재 우리는 이러한 양자 현상들을 이용하여 계산에 활용하는 양자 컴퓨터라는 완전히 새로운 개념의 컴퓨터나 양자 통신이라는 새로운 암호 통신 체계를 개발하여 십수 년 내에 사용할 것으로 기대하고 있다.
생물체와 양자역학을 연결하려는 시도는 의외로 양자역학의 태동 시기부터 있어 왔다. 슈뢰딩거 방정식으로 너무나 잘 알려진 어빈 슈뢰딩거Erwin Schrodinger는 1944년 그의 책 <생명이란 무엇인가?>에서 이미 양자역학과 생물체와의 관계에 대하여 논하였고 심지어 양자도약이라는 개념으로 돌연변이 현상을 설명하려고 시도했다. 보어 원자 모델로 유명한 닐스 보어도 양자역학의 상보성원리와 생물학 원리를 접목하려고 시도했고 1963년 뢰딘Per-Olov Löwdin이라는 이론 물리학자는 양성자의 터널링 효과가 DNA 돌연변이를 일으키는 기작 중 하나라고 주장하며 양자 생물학quantum biology이라는 용어를 처음 등장시켰다.
하지만 양자역학의 태동기부터 최근까지 양자역학과 생물학의 만남은 개념적인 상태에 머물러 있었다. 생체는 매우 많은 분자들이 상호 작용하는 복잡계이다. 그리고 우리의 체온에서 보듯이 생체온도는 양자현상이 일어나기에는 상당히 높은 편이다. 또한 양자 중첩 상태를 유지하기에는 너무나 많은 방해꾼, 즉 물과 단백질과 같은 환경으로 둘러싸여 있다. 그렇기에 그동안 과학자들은 생체 내에서 양자현상이 어떤 역할을 할 것이라는 기대를 많이 하지 않았다. 또한 복잡한 생체를 양자역학적으로 설명하는 데에는 기술적인 한계도 있었다.
하지만 2000년대에 들어서 여러 연구를 통하여 생체가 위에서 언급한 양자현상들을 이용하여 생존하고 있다는 연구 결과들이 보고 되었고, 이 현상들을 설명하기 위한 양자 가설들이 등장하면서 양자생물학이 주목받게 되었다. 생물체가 어떻게 양자현상을 이용하여 생존하고 있는지 각각의 대표적인 예를 양자 가설과 함께 살펴보자.1
양자 얽힘quantum entanglement
유럽의 로빈한국명 지빠귀이라는 귀여운 새는 지구의 자기장을 감지하여 여행하는 것으로 잘 알려져 있다. 이처럼 새가 생체 나침반을 이용하여 여행하는 현상은 1960년대부터 잘 알려진 사실이나 최근 이 현상을 설명하기 위한 유력한 가설로 양자 얽힘 현상이 사용되고 있다. 양자 얽힘은 고전적으로는 설명할 수 없는 입자들 간의 특수한 상관관계로, 예를 들어 두 개의 얽힘 상태에 있는 입자들이 있을 때 하나의 입자 상태가 결정되면 입자 간의 거리와 상관없이 다른 입자의 상태가 영향을 받는다는 것이다. 로빈의 눈에는 크립토크롬이라는 단백질이 있다. 광자가 로빈의 눈에 들어오면 크립토크롬에 의해 짝지은 라디칼이 만들어지고 이곳에 있는 얽힘 상태의 전자쌍이 지구의 자기장과 상호작용 하게 되어, 결국 빛에 의한 서로 다른 신경자극으로 로빈은 자기장을 느낄 수 있게 되는 것이다. 양자 얽힘은 뒤에 등장할 양자컴퓨터의 핵심 개념이다.
양자 터널링quantum tunneling
다음으로 이야기하고자 하는 양자 터널링의 예는 양자 얽힘 현상보다 우리가 매순간 경험하는 익숙한 일이다. 바로 냄새이다. 우리에게 아주 익숙한 현상임에도 우리가 어떻게 냄새를 맡는가에 대해서 아직까지도 밝혀져야 할 것이 많다. 과학적인 호기심에 더하여 향수회사 같은 산업계에서 냄새의 기작에 대한 연구에 많은 연구비를 투자하고 있다. 우리 코에는 390여개의 냄새 리셉터가 있는데 냄새 분자들에 의하여 활성화되거나 비활성화된다. 예를 들어 1번, 99번, 201번, 390번 리셉터가 활성화되면 민트향을 느끼게 된다. 이렇게 리셉터가 처리할 수 있는 조합은 2390(~10117)개로 바둑판 조합(~10172) 보다는 작지만 우주의 총 원자수(~1078) 보다 많다. 놀랍게도 우리 뇌가 구분해내는 냄새는 10만여 개로 리셉터 조합에 비해 너무 작다. 이렇게 엄청나게 많은 신호 속에서 아주 작은 냄새 신호를 구분해내는 것은 매우 놀라운 일이 아닐 수 없다. 어떻게 냄새 신호를 우리 뇌가 처리하는지 또 왜 그렇게 많은 리셉터가 필요한지에 대한 연구는 매우 흥미로운 주제임에 틀림없다.
이야기가 좀 곁길로 빠졌는데 다시 본론으로 돌아가면, 냄새 리셉터가 활성화되는 기작에 양자 터널링 효과가 관여한다는 가설이 있다. 리셉터가 냄새 분자에 의해 활성화되는 전통적인 기작은 열쇠-자물쇠 가설로 냄새 분자의 모양과 리셉터의 활성화가 관련되어 있다고 보는 것이다. 하지만 이 가설로는 냄새를 다 설명할 수 없다. 수소의 동위원소인 중성자가 하나 더 있는 중수소로 치환된 분자의 경우 열쇠-자물쇠 가설이 옳다면 냄새 분자의 모양이 같기에 같은 냄새가 나야 하는데 두 분자는 다른 냄새를 낸다.
또 다른 가설인 분자 진동-양자 터널링 가설로 이 현상을 설명할 수 있다. 고전적으로 에너지가 낮은 입자는 높은 에너지를 가지는 벽을 통과할 수 없지만 양자역학적으로는 가능하다. 주사 터널링 현미경Scanning Tunneling Microscope이 양자 터널링 효과를 이용한 대표적인 장비로, 매우 작은 샘플의 표면을, 진공벽을 넘어서 샘플로 흘러가는 전류의 양을 유지하기 위해 금속 팁으로 샘플과의 거리를 일정하게 유지하면서 훑으며 이미지화하는 기기이다. 주사 터널링 현미경처럼, 양자 터널링 효과로 인해 냄새 분자에서 리셉터로 전자가 흘러가게 되는데 이때 리셉터와의 에너지 차이만큼 정확하게 공진하는 양자화된 진동 모드에 에너지를 분배하면서 리셉터가 활성화된다. 이렇게 양자화된 분자의 진동운동으로 특정한 진동 모드가 아니면 냄새 리셉터를 활성화할 수 없다. 따라서 중수소로 치환된 분자의 냄새와 기존 분자의 냄새는 진동 주파수가 다르기에, 다른 냄새 리셉터를 활성화하여 다른 냄새를 내게 된다는 것이다. 이처럼 우리 코는 냄새 분자의 양자화된 진동운동을 느끼게 되는 것인데, 적외선 분광기나 라만 분광기의 원리와 비슷한 원리로 작동하고 있는 것으로 볼 수 있다.
양자 중첩quantum superposition
양자 중첩은 가장 근본적인 양자 현상으로 여러 개의 양자 상태가 확률적으로 공존하는 현상을 말한다. 고전적으로 설명할 수 없는 이 현상이 광합성에 중요한 역할을 할 수 있다는 것은 놀라운 일이다. 풀과 나무가 일반적으로 광합성을 하는 사례지만, 여기서는 조금 특별한 예를 소개하고자 한다. 바로 초록-황-박테리아GSB: green sulfur bacteria이다. GSB는 광합성을 통해 생명을 유지하는 박테리아로 수심 100미터 정도의 흑해 바닥에 살고 있다. 예상할 수 있듯이 흑해 바닥은 매우 어두워서 광합성으로 살아가는 GSB에게는 매우 척박한 환경이다. 실제로 GSB는 초당 불과 100여 개의 광자를 받는다. 100여 개의 광자는 우리가 받는 빛의 양에 비하면 천문학적으로 적은 양이다. 그렇기에 GSB는 받은 광자 에너지를 잃어버리지 않고 효율적으로 저장해야 한다.
실제 과정은 매우 효율적으로 양자 중첩으로 설명된다. GSB는 다른 광합성체와 마찬가지로 빛을 모으는 안테나를 가지고 있는데 척박한 환경에 맞게 구조가 매우 독특하다. 박테리아 클로로필이라 불리는 분자의 구조체로 이루어져 있는데 이 구조가 어떤 기하학적인 구조로 이루어져 있느냐에 따라서 흡수하는 빛의 파장영역과 흡광력이 다르다. 박테리아 클로로필 단일분자는 상대적으로 짧은 파장, 즉 높은 에너지 영역의 광자를 흡수하지만, 여러 분자가 모인 구조체의 경우는 흡광 영역이 빛이 상대적으로 풍부한 낮은 에너지 쪽으로 변하고, 그러면서 흡광하는 능력도 모인 분자 수의 제곱에 비례할 정도로 증가된다. 즉 GSB가 빛을 모으는 데 이용하는 안테나는 빛을 최대한 많이 받게끔 설계되어 있다.
GSB의 안테나 복합체는 3차원의 두루마리 구조체, 쟁반 모양의 2차원 구조체, 와이어 스타일의 1차원 구조체, 그리고 리액션 센터라고 불리는 0차원의 구조체로 이루어져 있는데, 이는 흡수하는 에너지가 높은 곳에서 점차 낮아지는 순서이다. 먼저 광자가 3차원 구조체에 도달하면 전자가 들뜨게 되고 전자가 비어있는 자리인 홀hole과 짝을 이루어 단일 입자처럼 행동하며 광자의 에너지를 GSB에 전달하게 된다. 이런 입자를 엑시톤exciton이라고 부르는데 엑시톤이 3차원 구조에서 2차원, 그리고 1차원 구조물을 거쳐 에너지를 주변 환경에 나눠주면서 결국 리액션 센터에 도달하게 되면, 엑시톤의 에너지가 화학 에너지로 변환되어 생체에 저장된다. 하지만 엑시톤은 3차원 구조체에서 만들어진 후 리액션 센터로 이동하는 과정에서 많은 단백질로 이루어진 진동하는 환경을 지나가야 하고, 그로 인해 엑시톤 자체가 유실될 가능성이 높다. 그렇기에 효율적인 에너지 전달을 위해서는 엑시톤이 사라지기 전에 리액션 센터로 빨리 내려가야 한다. 하지만 고전적으로 빨리 효율적으로 리액션 센터로 내려가는 길을 찾는 현상은 설명이 잘 되지 않는다.
여기서 양자 중첩이 핵심적인 역할을 한다. 즉, 하나의 광자가 여러 개의 박테리아 클로로필 분자를 동시에 들뜨게 하여 중첩된 엑시톤 상태를 만들고, 넓은 영역에 걸쳐 엑시톤이 편재하게끔 만든다. 이것은 마치 혼자서 길을 찾기 어려우니 여럿이서 같이 길을 찾는 것과 같은 효과를 준다. 뒤에서 이야기하겠지만 양자 컴퓨터의 병렬성과 관련이 깊다. 이렇게 엑시톤은 양자 중첩성을 이용하여 효율적으로 리액션 센터로 가는 길을 찾을 수 있고, 이것이 GSB가 흑해 바닥의 척박한 환경에서 살아갈 수 있는 비결이다.
GSB의 양자 중첩을 이용한 엑시톤 전달 과정을 이해하기 위해서는 이론적인 모델 연구가 필요하다. 하지만 GSB의 안테나 복합체를 모델링하여 양자역학적인 기작을 연구하는 것은 매우 어려운 일이다. 이론적으로 요구되는 홀스타인 모델Holstein model이라고 불리는 양자 모델을 정확히 풀어내기 위해서는 많은 계산 자원이 필요한데, 현재의 컴퓨터 능력으로는 기껏해야 수십 개 정도로 구성된 박테리아 클로로필 구조체를 다룰 수 있을 뿐이다. 이는 보통 몇만 개의 박테리아 클로로필로 이루어진 광합성 안테나 복합체를 다루기에는 턱없이 부족한 크기이다. 즉, 어느 정도 시스템 규모가 커지면 고전 컴퓨터로는 다차원의 양자 동역학을 정확히 다룰 수 없게 된다. 왜냐하면 시스템 크기에 따라서 필요한 계산자원이 지수적으로 증가되기 때문이다.
1929년 폴 디락Paul Dirac이 선언했듯이 화학을 이해하는 기본적인 원리는 양자 역학의 발견으로 이미 다 밝혀졌지만, 여전히 남은 문제는 이 풀기 어려운 문제를 물리적으로 합리적인 여러 가정을 통하여 풀 수 있는 문제로 치환해서 풀어내는 데 있다. 하지만 디락의 선언으로부터 90년이 지난 지금도 우리는 분자와 재료 문제를 해결하기 위해 슈뢰딩거 방정식을 풀고자 엄청난 노력을 하고 있다. 실제로 계산화학과 계산재료과학은 날씨 연구 다음으로 슈퍼 컴퓨터의 계산 자원을 많이 사용하고 있다. 이렇게 다체 양자 동역학quantum many-body dynamics의 계산이 어렵기 때문에, 1982년 리차드 파인만Richard Feynman이, 제어 가능한 양자 시스템이 다른 양자 시스템을 모사하는 양자 시뮬레이터quantum simulator라는 개념을 도입한 이후 지금까지 양자 컴퓨터 또는 양자 시뮬레이터와 관련한 연구가 활발히 이루어지고 있다.2
이런 큰 규모의 문제를 다루기 위해 필자는 다체 양자 문제를 모사할 수 있는 초전도 회로 기반의 양자 기기를 설계하는 연구에 참여하였다. 초전도 회로는 현재 이온 트랩ion trap, 양자 광학quantum optics 시스템과 함께 양자 컴퓨터를 만들 수 있는 가장 각광받는 양자 프로세서 중 하나로 구글과 IBM에서 활발한 연구를 진행하고 있다. IBM은 IBM Q라고 불리는 클라우딩 서비스를 일반인들에게도 제공하고 있어 독자들이 관심이 있다면 바로 사용해볼 수 있다. 광합성 양자 시뮬레이션 문제로 이미 언급했듯이 하나의 양자 시스템을 제어 가능한 양자 시스템 문제로 변환하여 모사하는 양자 기기를 아날로그 양자 시뮬레이터라고 부른다. 아날로그 양자 시뮬레이터의 반대개념으로 일반적으로 양자 컴퓨터라고 불리는 디지털 양자 시뮬레이터가 있다.
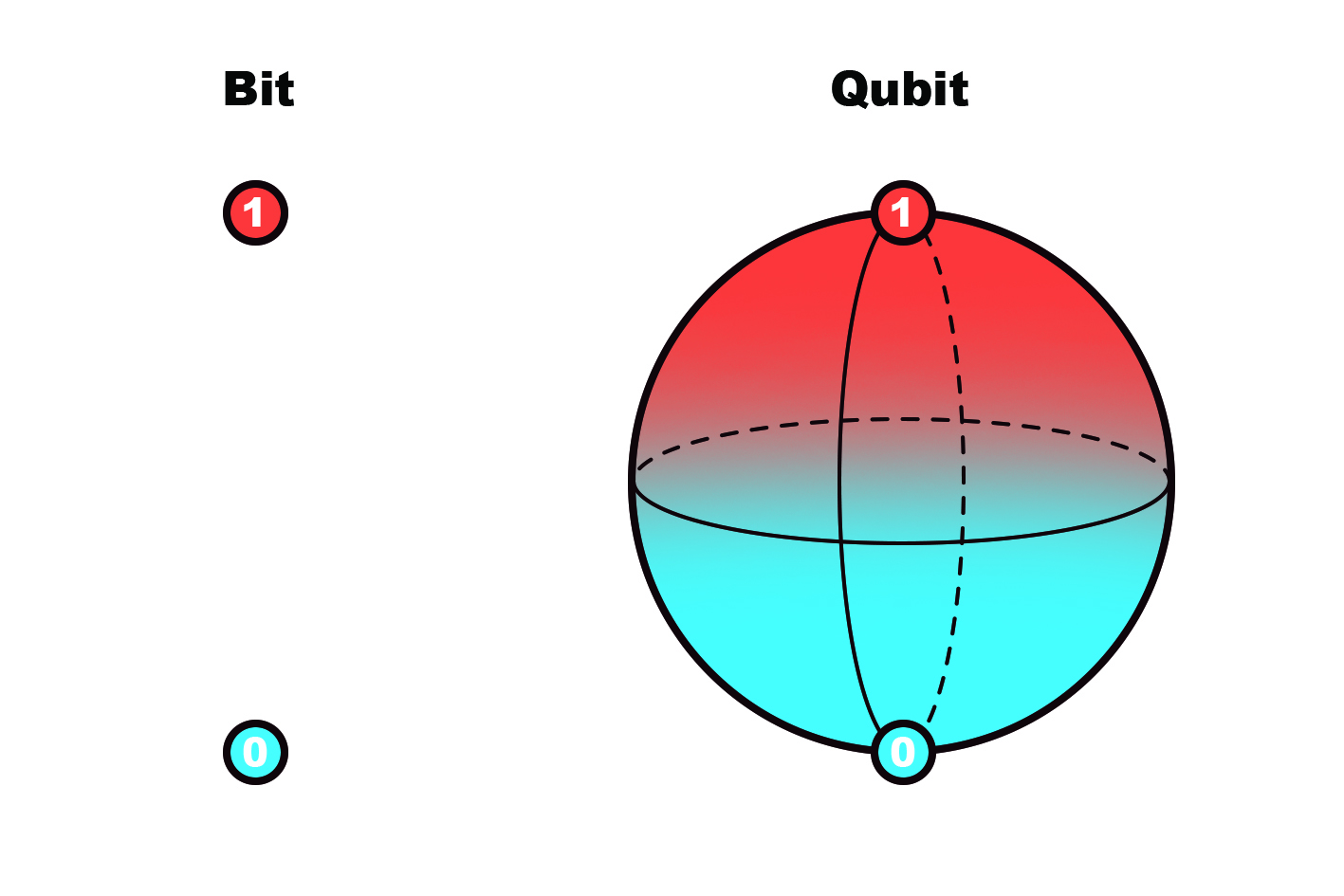
양자 컴퓨터는 큐비트qubit에 기반을 둔 양자 알고리즘을 이용하여 특정 문제들을 고전 컴퓨터보다 효율적으로 풀어낼 것으로 기대된다. 큐비트는 고전적인 비트인 0과 1의 중첩상태로, 만약 50개의 큐비트가 있다면 중첩 효과로 인하여 양자 컴퓨터는 250개의 50비트짜리 정보를 한 번에 처리할 수 있다. 이를 양자 병렬성quantum parallelism이라고 부른다. 양자 알고리즘은 양자 중첩성과 양자 얽힘을 계산과정에 이용하여 효율적인 계산을 수행할 수 있는 알고리즘을 말하며, 이러한 양자 알고리즘을 구동할 수 있는 장치를 양자 컴퓨터라고 부른다. 수년 내에 50-100큐비트 규모의 장치가 만들어질 것으로 기대되며, 중요 응용 분야로 양자 화학이 고려되고 있다.
하지만 지금까지 개발된 양자 알고리즘은 아직 많지 않아서 더 많은 알고리즘이 개발되어야 한다. 그중 가장 잘 알려진 양자 알고리즘은 쇼어 알고리즘Shor algorithm이라고 불리는 소인수 분해 알고리즘이다. 2000년대 초에 자기 공명 장치를 이용하여 (너무나 명확한 문제이기는 하지만) 분자 양자 컴퓨터가 15를 3과 5로 소인수 분해하는 것이 실험적으로 보여졌다. 아주 큰 정수를 소인수 분해하는 것은 NP 문제로 분류되는데, 이런 종류의 문제는 답을 구하는 것은 어렵지만 그 답을 확인하는 것은 쉬운 문제로써, 우리가 사용하는 암호 통신의 근간이 된다. 하지만 쇼어 알고리즘의 발견으로 양자 컴퓨터가 소인수 분해를 빠르게 할 수 있다는 것이 알려지면서 암호 통신의 근간이 흔들리게 되고 아직 큰 규모의 양자 컴퓨터는 없지만, 양자 알고리즘의 존재만으로도 우리는 이미 양자 암호 해독을 대비해야 하는 시대에 살고 있다. 이 때문에 여러 나라의 국가 정보기관들과 정보통신 업체들이 앞다투어 해킹당할 수 없는 양자 얽힘을 이용한 양자 암호 통신 기술개발에 박차를 가하고 있다. BB84와 같은 양자통신 프로토콜을 기반으로 이미 양자 통신 장비들이 시장에 나와 있고 중국 등 몇 나라들은 양자 통신 위성을 쏘아 올리기도 했다.
다체 양자 동역학을 모사하기 위한 양자 알고리즘은 개별 양자 프로세서의 특성을 고려하여 큐비트 기반의 양자 회로를 구성하여 만들어진다. 예를 들어 양자 컴퓨터에서 분자를 모사한다고 할 때 페르미온인 전자를 수학적으로 큐비트의 언어, 즉 파울리 행렬Pauli matrix로 변환하여 회로가 구성된다. 이때 사용되는 수학적인 변환 방법에는 여러 가지가 존재하는데, 어떤 변환 방법을 사용하느냐에 따라 회로의 길이와 큐비트 간의 연결 관계가 다르게 결정되기에 해당 양자 컴퓨터의 물리적인 특성을 고려하면서 양자 알고리즘을 구현해야 한다. 일반적으로 양자 중첩 상태를 계산 도중에 유지하기 위하여 양자 회로를 최대한 짧게 하고 물리적으로 멀리 떨어진 큐비트 간의 연결이 많이 필요하지 않은 양자 회로를 선호한다. 최근 2-3개의 원자로 이루어진 분자에 대한 양자화학 문제가 양자 광학과 초전도 회로 기반의 양자 컴퓨터에서 모사되었다. 또한 작년에는 분자의 진동 문제가 양자 광학 시스템에서 모사되었고, 필자가 제안한 양자 광학을 이용한 분자의 양자 샘플링 알고리즘이 양자광학과 양자 광학을 모방한 이온 트랩 장치에서 구현되어 양자 기기가 분자의 바이브로닉 (전자+진동) 스펙트럼을 모사할 수 있다는 것이 보여졌다.
이렇듯 양자 컴퓨터에 대한 기대가 높지만, 양자 컴퓨터가 모든 문제를 빨리 풀어낼 수 있는 마법사가 아니라는 것을 명확히 하고 싶다. 양자 컴퓨터는 특정 부류에 속한 문제들만 효율적으로 풀어낼 수 있다. 하지만 그동안 인류가 고전 컴퓨터로는 도저히 접근할 수 없었던 앞서 언급한 양자 생물학 문제를 포함하여 화학, 물리, 생물, 재료, 사회, 경제와 관련한 수리과학 문제를 양자 컴퓨터를 이용하여 도전할 수 있다는 데 큰 의미가 있다. 십수 년 내에 그동안 만들어내지 못했던 데이터들을 양자 컴퓨터가 생산하게 될 것이고 인공 지능 기법들과 상호 보완적으로 역할을 담당함으로써 우리의 미래 생활에 큰 영향을 줄 것이다. 또한 인공 지능과 관련하여 선형 방정식을 효율적으로 풀 수 있는 양자 알고리즘의 개발로 양자 머신 러닝이라는 양자 알고리즘 연구가 활발히 진행되고 있다. 따라서 머지않은 미래에 인공지능의 빅데이터 처리 또한 양자 컴퓨터의 도움을 받아서 수행하게 될 날이 올 것이다.
지금까지 양자 정보가 어떻게 다양한 시스템에 이용될 수 있는지를 생물체와 양자 컴퓨터의 사례를 통해 간략히 소개하였다. 양자 생물학의 가설들이 옳다면 생물체도 양자 컴퓨터처럼 양자 정보를 처리하는 장치라고 볼 수 있다. 이렇게 두 시스템은 비슷한 부분도 있지만 재미있는 중요한 차이가 있다. 양자 컴퓨터에서는 주변 환경과의 상호 작용으로 양자 중첩성을 잃어버리는 양자 결잃음decoherence 현상이 양자 계산의 가장 큰 걸림돌이고 현재 양자 컴퓨터 설계에서 가장 먼저 고려해야 할 점이다. 하지만 생물 시스템은 상황이 다르다. 생물 시스템은 양자 컴퓨터와는 다르게 복잡한 주변 환경으로부터 오는 양자 결잃음 현상까지도 이용하여 생명유지에 이용할 가능성이 있기 때문이다. 이렇게 본다면 생물 시스템이 정보 처리에 있어서 인공적인 양자 컴퓨터보다도 우수해 보인다. 여기서 필자는 영화에서나 나올 법한 박테리아 양자 컴퓨터를 상상하며 양자정보 이야기를 끝내겠다.