패턴의 과학 [2]: 패턴의 정보량과 엔트로피

들어가며

지난 “패턴의 과학 [1]: 패턴의 자기닮은꼴과 프랙탈 차원”에서는 패턴의 자기닮음꼴과 프랙탈 특성에 대한 내용을 소개했다. 자연이나 인공적으로 생성된 자기닮음꼴 패턴의 프랙탈 차원을 계산하는 방법, 혹은 역으로 프랙탈 특성을 알고 있을 때, 인공적으로 프랙탈 패턴을 만든 방법 등에 대해 논했다. 패턴의 복잡도를 측정하는 목적만 놓고 보았을 때, 프랙탈 차원 자체는 중요한 정보를 제공하긴 하나, 그 정보가 패턴이 가진 복잡도와 정보량 전부를 커버할 수 있는 것은 아니다. 무엇보다 프랙탈 차원이라는 개념은 국소적인 자기닮음꼴이 척도 불변^{scale-invariance} 조건에서 나타나는 특성이기 때문에 전역적으로 무질서도가 어떻게 분포하고 있는지, 그 정도는 얼마나 차이가 나는지, 자기닮음꼴이 척도에 따라 유지가 안 되는 경우는 어떻게 복잡도를 계산할 것인지 등의 문제까지 해답을 줄 수 있는 것은 아니다. 따라서 이에 대한 해답을 줄 수 있는 정량적인 지표가 필요하며, 그중 가장 대표적인 지표로 엔트로피를 생각할 수 있다. 이번 “패턴의 과학 [2]: 패턴의 정보량과 엔트로피”에서는 패턴이 갖는 정보량과 복잡도를 어떠한 방식으로 계산할 수 있는지, 엔트로피 계산을 중심으로 접근하는 방법에 대해 논할 것이다.

허스트 지수^{Hurst exponent}

20세기 중반 영국의 토목공학자이자 이집트 나일강 유역 홍수 관리 담당관이기도 했던 해롤드 허스트^{Harold E. Hurst}에게 도도히 흐르는 나일강은 평화롭게 바라만 볼 수 있는 대상은 아니었다. 홍수 관리 담당관이라는 직무에서도 알 수 있듯 그가 하던 일은 매년 범람을 반복하는 나일강 홍수 규모를 기록하고 예측하는 것이었다. 잘 알려져 있다시피 나일강 범람 규모의 변동은 예측할 수 없을 정도로 들쑥날쑥하여, 때로는 비옥한 토지를 제공해 주는 이집트 문명의 토대가 된 젖줄이 되기도 했지만, 때로는 주민의 생명과 재산을 앗아가는 가혹한 재앙이 되기도 했다. 이에 대한 대비책을 세우는 것은 수천 년 전부터 정부 관리들의 주된 책무 중 하나였다.

허스트는 그간 누적된 수백 년간의 나일강 범람 규모 데이터를 꼼꼼하게 살펴보던 중 흥미로운 특성을 발견했는데, 그것은 나일강 범람 데이터에 보일 듯 말듯 감춰져 있던 일종의 ‘장기 기억^{long-term memory}‘이었다. 이를 통계적으로 분석하기 위해 허스트는 샘플링^sampling 기법을 활용했다. 보다 상세히 설명하자면, 전체 데이터에서 일부 구간만 추출한 샘플 데이터의 표준편차와 평균을 이용하여 샘플 데이터를 누적 편차 데이터로 변환하고, 이로부터 샘플 데이터의 ‘범위^range (\(R\))’라는 개념을 정의한 후 이를 표준편차 (\(\sigma\))로 정규화한 ‘축도조정범위^{rescaled range} (\(RS\))’라는 통계학의 샘플링 개념을 도입한 것이다.[1]

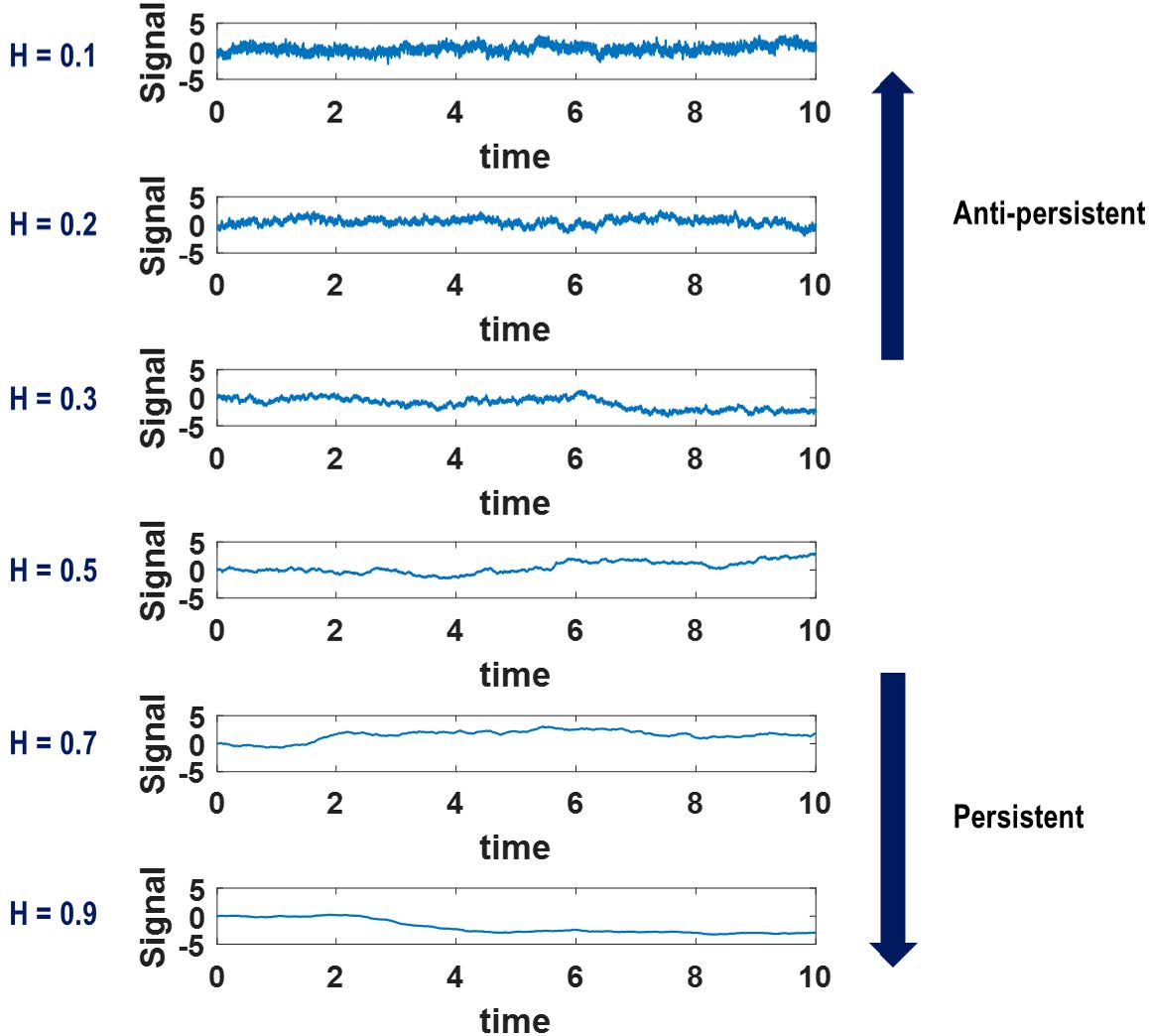
허스트는 이 축도조정범위들의 평균값 \(E(R/\sigma)\)이 샘플 데이터의 크기 \(n\)에 대해 멱함수 의존성^{power-law dependence}, 즉, \(E(R/\sigma) \sim n^H\)의 관계를 가짐을 경험적으로 발견했는데, 이 때 지수 \(H\)를 ‘허스트 지수^{Hurst exponent}’라고 부른다. 허스트 지수는 나일강의 범람 규모 기록 같은 1차원 시계열 데이터의 변동 양상이 어떤지를 보여 주는 정성적 지표 역할을 한다. 먼저 \(0 \leq H \leq 0.5\)인 경우, 데이터는 ‘추세 회귀적^{anti-persistent or negatively correlated} 경향’을 보이는데, 다시 말해 상승이 있으면 반드시 하강이 뒤따르는 구조라는 의미다.

예를 들어 어떤 아파트의 월별 시가 변동 데이터의 허스트 지수가 \(H = 0.3\)이라고 할 때, 아파트 시가가 특정 구간에서 계속 상승 기조를 보였다면 아파트 시가는 시간이 지남에 따라 다시 하강할 확률이 높다고 볼 수 있다. 이는 등락폭의 변동이 커져야 함을 의미하는 것이기도 하다. 그러나 허스트 지수가 \(0.5 \leq H \leq 1\)인 경우에는 ‘추세 지속^{persistent or positively correlated} 경향’이 보이는데, 이는 상승한 기조는 계속 상승, 하강하는 기조는 계속 하강하려는 경향이 있음을 의미한다. 달리 말하자면 데이터의 변동 폭이 상대적으로 작을 것임을 의미한다. \(H = 0.5\)인 경우는 데이터의 변동이 완전히 ‘무작위적^{not-correlated}’인 ‘비너 과정^{Wiener process}’ 혹은 ‘이상적 브라운 운동^{ideal Brownian motion}’에 해당하는 경우이며 이 경우, 데이터 변동은 완전히 무작위적인 양상을 보인다.

자기닮음꼴이 내재된 데이터나 패턴의 프랙탈 차원은 허스트 지수 \(H\)와 흥미로운 연관성을 갖는다. 예를 들어 자기닮음꼴을 갖는 데이터로서 ‘프랙탈 브라운 운동 데이터^{fractal Brownian motion or fractional Brownian motion, fBm}’를 생각할 수 있다. ‘마구잡이 걷기^{random walk}’를 하는 입자의 운동을 의미하는 ‘브라운 운동^{Browninan motion}’에서 비롯된 이 개념은 시간에 지남에 따라 데이터의 변동이 ‘제어된 수준에서’ 마구잡이로 형성되는 것을 상정하여 데이터가 생성된다. 허스트 지수 \(H\)가 미리 주어졌을 때, fBm 데이터 \(B(t)\)는 다음과 같은 자가상관함수^{autocorrelation function} 혹은 공분산 함수^{covariance function} 특성을 갖는다.

\begin{align}
\begin{matrix}
\langle B(t+\tau)B(t) \rangle = \frac{V_H}{2}(|t|^{2H}+|t+\tau|^{2H}-|\tau|^{2H}), \, \\
V_H = \Gamma(1-{2H})\frac{cos(\pi H)}{\pi H}
\end{matrix}
\quad \cdots \quad (1)\end{align}

위에서 \(\tau\)를 ‘시차^{time lag}‘라고도 한다. \(\Gamma(x)\)는 감마함수^{gamma function}를 의미한다. 위 식을 이용하면

\begin{align}
\begin{matrix}
\langle (B(t+\tau)-B(t))^2 \rangle \\
= \langle B(t+\tau)B(t+\tau) \rangle -2\langle B(t+\tau)B(t) \rangle +\langle B(t)B(t) \rangle \\
= {V_H}|\tau|^{2H}
\end{matrix}
\quad  \cdots \quad (2)\end{align}

임도 유도할 수 있다. 따라서 1차원 fBm의 분산 \(\langle \Delta B(\tau)^{2} \rangle\)은 시차 \(\tau\)에 대해 지수 \(2H\)를 갖는 멱함수 관계^{power-law dependence}를 가짐을 알 수 있다. 이를 이용하면 1차원 fBm 데이터의 등락폭 \(\Delta B(\tau)\)은 다음과 같은 확률 분포를 가짐을 알 수 있다.

\begin{align}
P(\Delta B(\tau) < z) = \frac{1}{\sigma_0^{H} (2\pi)^{0.5}} \int_{-\infty}^{z} exp(-\frac{x^2}{2(\sigma_0 \tau^{H})}) dx
\quad \cdots \quad (3)\end{align}

1차원 fBm의 등락폭 확률 분포를 이용하면 주어진 \(H\) 값에 대해 1차원 fBm 데이터 \(B(t)\)를 다음과 같은 알고리즘을 이용하여 인공적으로 만들 수 있다.

1. 데이터의 크기 \(N\)을 정한다. 첫 번째 지점 \(B(1)\)과 끝 지점 \(B(N)\)에 정해진 범위 내의 임의의 값을 배정한다.
2. 전체 데이터를 이등분한 후, 절반 지점인 \(B(\frac{1+N}{2})\)에는 \(\frac{B(1)+B(N)}{2}\)을 배정하여 데이터를 이등분하되 그 값에 표준편차 \(\sigma_0\), 평균 0을 갖는 가우시안 확률 분포 난수^{Gaussian random number}를 배정한다.
3. 이등분된 데이터 두 토막을 다시 이등분하여 \(\frac{1}{4}\)짜리 데이터 네 토막을 만들고 두 번째 단계의 값을 설정한다. 단, 이때의 표준편차는 \(\frac{\sigma_0}{2^H}\)로 정한다.
4. 2-3단계 과정을 반복하면 크기 \(\frac{1}{2^k}\)짜리 데이터 \(2^k\) 토막을 만들고 표준편차는 \(\frac{\sigma_0}{2^{(k-1)H}}\)로 정하면, 자기닮음꼴을 유지하면서도 변동의 특성이 축척에 상관 없이 특정 허스트 지수 \(H\)를 갖게끔 제어된 1차원 fBm 데이터를 생성할 수 있다. [그림1]은 허스트 지수 \(H\)가 증가할 때 어떻게 1차원 fBm 데이터의 변동폭이 줄어드는지를 보여준다.
   
   

참고로 1차원 fBm 데이터에서 바로 인접한 이웃 데이터 성분들 사이의 변동^{difference, 차분값}, 즉, \(C(t) = B(t+1) – B(t)\)도 자기유사성을 갖는데 이러한 차분값 데이터를 ‘프랙탈 가우시안 잡음^{fractional Gaussian noise, fGn}‘이라고 부른다. 1차원 fGn 데이터가 자기유사성을 갖기 때문에 fGn의 자가상관함수 역시 멱함수 의존성을 가질 것을 쉽게 예상할 수 있다. 왜 그렇게 되는지 알아보자. 우선 fGn의 공분산 함수 \(\langle C(t+\tau)C(t) \rangle\)는

\begin{align}
\begin{matrix}
\langle C(t+\tau)C(t) \rangle \\
= \langle (B(t+1+\tau)-B(t+\tau))(B(t+1)-B(t)) \rangle \\
= \frac{V_{H}|\tau|^{2H}}{2} (((1+\frac{1}{\tau})^{2H}) + ((1-\frac{1}{\tau})^{2H}) -2) \sim 2H(2H-1)V_{H}\tau^{2H-2}
\end{matrix}
\quad \cdots \quad (4)\end{align}

임을 유도할 수 있다. 즉, fGn 데이터의 자가상관함수는 \(\langle C(t+\tau)C(t) \rangle \sim \tau^{2H-2}\) 같이 시간 간격 \(\tau\)에 대해 멱함수 의존성을 갖는다는 것을 알 수 있다. 또한 fGn의 자기상관함수의 멱함수 의존성을 이용하면 fBm의 자기상관함수 멱함수 의존성도 \(\tau\)에 대해 \(\langle B(t+\tau)B(t) \rangle \sim \tau^{2H}\)의 형태가 될 것임을 유도할 수 있다.

흥미롭게도 ‘비너-킨친 정리^{Wiener–Khinchin theorem}‘에 따르면[2] 자기닮음꼴 특성이 있는 1차원 데이터를 주파수 공간에서 푸리에 변환^{Fourier transform}한 데이터는 주파수에 대해 멱함수 의존성을 갖는데, 1차원 데이터 \(Y(t)\)에 대해 이들의 자가상관함수가\[\langle Y(t+\tau)Y(t) \rangle \sim \tau^{\gamma_Y}\]같이 지수 \(\gamma_Y\)와 연계된 멱함수 관계를 가지고 있을 때, 이들의 푸리에 변환도 주파수 공간에서 주파수 \(f\)를 갖는 신호의 강도가 전체 신호 강도에서 차지하는 분율 \(P(f)\)는

\begin{align}
P(f) \sim f^{-\beta_Y}, \beta_Y=1-\gamma_Y
\quad \cdots \quad (5)\end{align}

의 멱함수 관계가 유도된다. 마찬가지로 1차원 fBm의 경우, \(\gamma_B = -2H\)이므로 \(\beta_B = 2H+1\)이 된다. 푸리에 변환의 멱함수 특성을 이용하면 허스트 지수 \(H\)가 정해진 fBm 데이터를 다음과 같은 알고리즘으로 생성할 수 있다.

1. 데이터의 길이 \(N\)을 정하고, \(N\)개의 지점에 정해진 범위 내의 난수를 배정한다.
2. 원본 데이터를 1차원 푸리에 변환한다. 
3. 변환된 주파수 데이터의 각 주파수별 강도^amplitude의 가중치들의 자가상관함수 분포가 \(f^{-\beta_B}\)를 따르게 스케일을 조정한다.
4. 조정된 주파수 데이터를 다시 역 푸리에 변환^{inverse Fourier transform}하여 fBm 데이터로 변환한다.

또한 1차원 fBm 데이터는 \(B(at) \sim |a|^H B(t)\)의 자기닮음꼴 특성이 있기 때문에, 이 fBm 데이터의 허스트 지수는 결국 데이터의 프랙탈 차원 \(D\)와 \(D+H=E+1\)의 관계를 보이게 된다. 여기서 \(E\)는 유클리드 차원^{Euclead dimension}을 의미하며 1차원 데이터는 \(E=1\)이므로 \(D=2-H\)이다. 이때 주의해야 할 점은 모든 1차원 데이터가 이러한 관계를 만족한다는 것은 아니라는 점이다. 1차원 데이터에 자기유사성이 없다면 프랙탈 차원과 허스트 지수는 전혀 연관성이 없다. 허스트 지수가 데이터의 전역적 특성^{global property}에 대한 지표이고 프랙탈 차원은 국소적 특성^{local property}에 대한 지표임을 고려하면, 어떤 데이터에 자기유사성이 없는 경우 두 지표 사이에 특별한 연관성이 있을 필요가 없다는 것은 쉽게 이해할 수 있다.

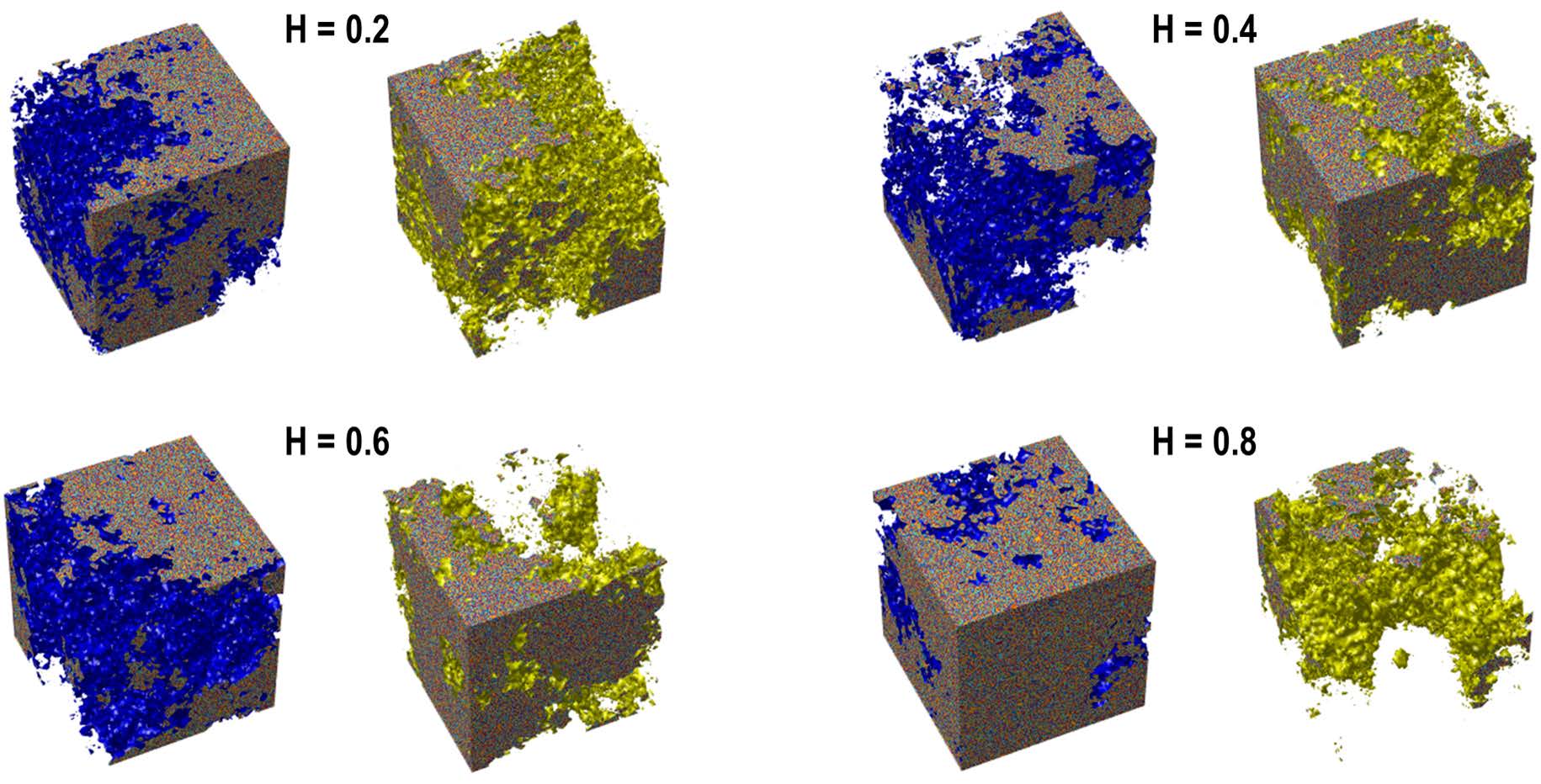
허스트 지수를 설정하여 1차원 fBm를 생성했던 알고리즘을 조금 더 응용하면 2차원 fBm도 생성할 수 있는데, 이는 “패턴의 과학 [1]: 패턴의 자기닮은꼴과 프랙탈 차원”에서 살펴보았던 프랙탈 지형^{fractal landscape} 같은 패턴의 생성 도구가 될 수 있다. “패턴의 과학 [1]: 패턴의 자기닮은꼴과 프랙탈 차원”에서 살펴보았던 ‘마름모-정사각형 방법^{Diamond-square method}‘에서는 격자 지점의 값을 생성할 때 인접한 격자 좌표들로부터 내삽된 값에 난수를 더하는 과정을 거쳤었는데, fBm 생성 알고리즘을 이용하면 자기닮음꼴을 유지하면서 난수 변동 범위를 제어할 수 있다. 예를 들어 [그림1]은 이러한 방법으로 생성된 프랙탈 지형(이를 fractal Brownian surface라고도 부른다)의 사례이다. 그림에서 볼 수 있다시피 \(H\)가 증가할수록 생성된 지형 표면의 거칠기가 완화되는 것을 확인할 수 있다. 2차원뿐만 아니라 비슷한 방식으로 3차원 이상의 자기닮음꼴 구조체도 생성할 수 있다. 2차원에서는 표면의 거칠기^{surface roughness}가 허스트 지수로 제어된 것 같이 3차원에서는 공간 내부 기공률^porosity 및 연결도^connectivity가 제어된 3차원 다공성 구조체^{porous structure} 혹은 3차원 세포형 네트워크 구조체^{cellular network structure}를 생성할 수 있다. [그림2]에는 허스트 지수 \(H\)가 커짐에 따라 3차원 프랙탈 다공성 구조체의 형태가 어떻게 변하는지를 보였다.

지금까지는 허스트 지수 \(H\)가 주어졌을 때 자기닮음꼴 데이터나 2차원 패턴 혹은 3차원 구조체를 인공적으로 생성하는 방법을 주로 알아봤지만, 이미 주어진 신호 혹은 자연에서 발견되는 패턴의 허스트 지수를 추출하는 것도 매우 중요한 작업이 될 수 있다. 다만 본래 허스트가 경험적 샘플링 방법으로 제안했던 \(RS\) 방법으로 추출한 결과로부터 계산한 허스트 지수는 데이터 크기가 상대적으로 작을 때 다소 부정확성이 누적될 수 있음이 밝혀진 후, 이에 대한 보완책이 몇 개 제안되었다. 그중 가장 대표적인 방법은 ’탈추이 변동분석^{Detrended Fluctuation Analysis, DFA}’라는 방법으로, 특히 1차원 데이터의 상관 길이(시계열 데이터의 경우 상관 시간)가 상대적으로 클 경우, 데이터의 자기유사성을 더 정확하고 정량적으로 측정할 수 있음이 알려져 있다.[3]

신호의 복잡도 측정

모든 신호와 패턴은 수학적으로 차원이 정해진 데이터라고 볼 수 있으며, 데이터의 구성 성분인 숫자들이 얼마나 규칙적인지 혹은 불규칙적인지에 따라 신호와 패턴의 정보량도 달라진다. 또한 정보량은 데이터의 복잡도^complexity와 관련이 있으며, 따라서 이러한 복잡도를 정량적으로 측정하는 것은 신호와 패턴에 대한 보다 깊은 이해를 가능하게 한다. 이를 통해 좁게는 데이터나 패턴의 재현 혹은 압축이 가능하고, 나아가 정량적인 맥락에서 서로 다른 데이터 혹은 패턴끼리의 비교도 가능하다. CT나 fMRI 같은 의료 영상장비에서 획득한 다차원 의료 이미지 데이터의 경우 이러한 정량적 비교는 환자의 병변 상황 판단과 이상 유무 검사 등에도 활용될 수도 있다.

기본적으로 데이터나 패턴의 복잡도를 이해하기에 가장 효과적인 방편 중 하나는 그들의 ‘엔트로피^entropy‘를 측정하는 것이다. 1948년, ‘정보이론 ^{information theory}‘의 아버지인 클로드 샤논^{Claude Shannon}이 ‘정보 엔트로피^{information entropy}‘ 개념을 처음 소개한 이후[4], 신호의 엔트로피라는 개념은 다양한 분야에서 활용되고 있다. 정보 엔트로피는 창안되었을 당시 본래의 목적이었던 신호의 정보량 측정은 물론, 데이터의 압축·복원 과정, 데이터의 복잡도 측정, 그리고 이미지의 무작위성이나 변형 유무 검사 등 다양한 목적으로 활용되고 있으며, 최근에는 딥러닝을 통한 데이터 해석 혹은 예측 품질의 검사 지표로도 활용되고 있다. 샤논이 제시한 정보 엔트로피 \(S\)는 통계물리학에서 다루는 엔트로피와 수학적으로는 같은 형태이다. (둘은 물리적 단위 유무의 차이만 있다.) 정보의 표본 공간이 N개의 서로 다른 값들로 구성되어 있고 각 값의 비율(혹은 확률 \(p_i, \, i=1,\,2,\, …\, N\))을 알고 있을 때, 정보 엔트로피 \(S\)는 다음과 같이 표현할 수 있다.

\begin{align}
S = -\sum_{i=1}^{N} p_{i} logp_{i}
\quad \cdots \quad (6)\end{align}

참고로 위의 식에서 사용된 로그의 밑은 용도에 따라 e, 10, 2 등을 쓸 수 있다. 예를 들어 디지털 신호는 이진 신호^{binary signal}이므로 보통 디지털 신호의 엔트로피는 로그의 밑을 2로 쓰며, 이를 통해 데이터의 정보량을 비트^bit나 바이트^byte 단위로 표현할 수 있다. 정보 엔트로피는 수학적 정의상 표본 공간이 균등하게 분배되었을 때, 다시 말해 모든 정보 값들의 구성 비율이 같은 값을 가질 때 (즉, \(p_i = \frac{1}{N}\)인 경우) 가장 큰 값인 \(\max(S) = logN\)을 갖는다. 그렇지만 정보 엔트로피에도 한계가 있으니 그것은 정보를 구성하고 있는 데이터 성분이 배열된 ‘경우의 수’에 대한 고려는 없다는 것이다. 예를 들어 두 데이터 쌍 \(X_1 = [1 \, 2 \, 1 \, 2 \, 1 \, 2 \, 1 \, 2 \, 1 \, 2 \, 1 \, 2]\)과 \(X_2 = [1 \, 1 \, 2 \, 1 \, 2 \, 2 \, 2 \, 1 \, 1 \, 2 \, 2 \,1]\)을 생각해 보자. 두 쌍의 데이터는 같은 크기를 가지고 있으며 모두 1과 2로만 정보가 구성되어 있고 각 성분의 분율은 0.5로 같다. 이를 고려하면, 두 데이터 쌍의 정보 엔트로피는\[S(X_1) =S(X_2) = -\sum_{i=1}^2 p_i logp_i = -2(0.5log0.5) = 0.693\]로 같은 값을 갖기 때문에, 정보 엔트로피만으로는 두 데이터의 복잡도 차이를 구분할 수 없다. 그렇지만 누가 봐도 \(X_1\)은 규칙적인 배열을 갖는 1차원 데이터(즉, 주기성이 확실하여 예측이 가능한 정보)인 데 반해 \(X_2\)는 불규칙적인 배열을 갖는 1차원 데이터(즉, 예측이 거의 불가능한 정보)라고 판단할 수 있다. 따라서 ‘복잡도’라는 개념을 정의할 수 있다면, 두 쌍의 데이터는 바로 이 ‘복잡도’에서 명확한 차이가 있어야 정상일 것이다. 그러므로 정보 엔트로피만으로는 구분할 수 없는 신호의 복잡도 차이를 구분할 수 있는 새로운 수학적인 방법이 필요하다.

이를 위해 이제부터 다양한 종류의 엔트로피 기반 복잡도 측정 방법에 대해 알아보자. 먼저 소개할 엔트로피는 ‘근사 엔트로피^{approximate entropy}‘라는 개념이다.[5] 이 엔트로피는 1차원 데이터의 복잡도를 측정하는 여러 종류의 엔트로피 중 하나로서, 데이터의 복잡도가 증가할수록 (즉, 예측 불가능성이 높아질수록) 산출되는 엔트로피 값도 비례하여 증가하도록 설계된 측정량이다. ‘근사’라는 명칭이 붙은 이유는 수학적으로 이상적인 복잡도 지표인 ‘콜모고로프-시나이 엔트로피^{Kolmogorov-Sinai entropy}‘를 근사한다는 의미에서 유래되었기 때문이다. 길이 \(N\)을 갖는 데이터 \(U = [u(1) \, u(2) \, … \, u(N)]\)에 대해, 근사 엔트로피는 다음과 같은 과정을 거쳐 계산할 수 있다.

1. 자연수 \(m\)을 정해서(이 숫자를 ‘임베딩 차원^{embedding dimension}‘이라고 부른다) 다음과 같이 길이 \(m\)의 샘플 데이터 \(X(i)\)를 생성한다.

\[
X(i) = [u(i) \, u(i+1) \, … \, u(i+m-1)], \, i=1,\, 2,\, …,\, N-m+1
\]

2. 1.에서 생성된 샘플 데이터를 모아 이들의 ‘평균 닮음도’ \(C_{i}^{m}(r)\)을 다음과 같이 계산한다.

\begin{align}
C_{i}^{m}(r) = \frac{number \, of \, X(j)\, s.t.\, d[X(i),X(j)] \leq r}{N-m+1}, d[X,X^*] = \max_{a}|u(a)-u^* (a)|
\quad \cdots \quad (7)\end{align}

위 식에서 \(d[X,X^*]\)는 두 데이터 벡터 \(X\)와 \(X^*\) 사이의 ‘스칼라 거리^{scalar distance}‘에 해당하는 값이다. 또한 \(r\)은 미리 정해 둔 ‘문턱 거리^{threshold distance}‘로, 이 거리보다 두 데이터 사이의 스칼라 거리가 작거나 같으면 두 데이터는 근사적으로 같다고 간주한다.

3. 2.에서 계산된 \(C_{i}^{m}(r)\)의 로그값의 평균 \(\langle log(C_{i}^{m}(r)) \rangle\)을 이용하여 누적 엔트로피 \(\Phi^{m}(r)\)를 다음과 같이 계산한다.

\begin{align}
\Phi^{m}(r) = \langle log(C_{i}^{m}(r)) \rangle = \frac{\sum_{i=1}^{N-m+1} logC_{i}^{m}(r)}{N-m+1}
\quad \cdots \quad (8)\end{align}

4. 3.에서 계산한 \(\Phi^{m}(r)\)을 이용하여 근사 엔트로피 \(S_{apen}\)을 다음과 같이 계산한다.

\begin{align}
S_{apen} = \Phi^{m}(r)-\Phi^{m+1}(r)
\quad \cdots \quad (9)\end{align}

위 알고리즘에 따라 규칙적인 특성을 갖는 데이터의 엔트로피가 정말 0에 가깝게 나오는지 알아보자. 예를 들어 어떤 사람의 1분당 심박수 데이터가 \(U = [85 \, 80 \, 89\, …\, 85 \, 80 \, 89],\, N = 51\)이라고 해 보자. 즉, 이 데이터는 주기가 3인 규칙적인 데이터라고 할 수 있다. 이에 대해 \(m=2\)인 경우와 \(m=3\)인 경우의 누적 엔트로피를 위 알고리즘으로 계산하여 둘의 차이를 계산하면

\[
S_{apen} = \Phi^{2}(r) – \Phi^{3}(r) = (-1.0982095…)\,-\,(-1.0981985…) = 1.09965 \times 10^{-5}
\]

이 나온다. 즉, 거의 0에 가까운 \(S_{apen}\)값이 산출된 것을 확인할 수 있다. 샘플 엔트로피 값이 정확히 0이 아닌 까닭은 애초 주어진 데이터의 길이가 무한하지 않았기 때문이다. 데이터의 길이가 길어질수록 규칙적인 데이터의 근사 엔트로피는 점점 0으로 수렴한다. 근사 엔트로피를 계산할 때, 보통 \(m\)은 2나 3을 쓰며 \(r\)은 원본 데이터의 표준편차 (\(\sigma\))보다 작은 값을 설정한다. 근사 엔트로피는 계산이 상대적으로 가볍고 데이터의 불규칙성을 잘 드러낼 수 있다는 장점이 있는 반면, 상대적으로 크기가 작은 데이터에 대해서는 데이터 크기에 대한 의존성이 강해지고 노이즈가 심한 데이터의 복잡도에서 노이즈의 영향을 제대로 가려낼 수 없다는 단점도 있다. 따라서 근사 엔트로피는 상대적으로 작은 노이즈 환경에서 상대적으로 크기가 큰 데이터의 불규칙성 비교 정도로 용도가 한정되는 경향이 있다.

두 번째로 알아볼 엔트로피는 ‘샘플 엔트로피^{Sample entropy}‘로, 이는 근사 엔트로피의 단점을 보완하면서도 비교적 정확하고 빠르게 데이터의 불규칙성을 찾아낼 수 있는 엔트로피다.[6] 원본 데이터 \(U\)의 샘플 데이터 \(X_i\)를 생성하고 \(d[X,X^*]\)를 계산하여 \(C_{i}^{m}(r)\)를 계산하는 과정까지는 근사 엔트로피와 같지만, 샘플 엔트로피 \(S_{saen}\)은 정규화된 \(C_{i}^{m}(r)\)의 로그값의 차이를 이용하여 엔트로피를 계산한다. 즉,

\begin{align}
S_{saen} = -log(\frac{\frac{\langle C_{i}^{m+1}(r) \rangle}{N-m+1}}{\frac{\langle C_{i}^{m}(r) \rangle}{N-m}})
\quad \cdots \quad (10)\end{align}

의 관계식으로 표현된다. 샘플 엔트로피의 수학적 정의상 항상

\begin{align}
C_i^{m+1}(r)(N-m) \leq C_i^{m}(r)(N-m+1)
\quad \cdots \quad (11)\end{align}

의 관계가 성립하기 때문에, \(S_{saen} < 0\)이 되는 경우는 없으며, \(C_{i}^{m}(r)\)를 정규화시킨 후 로그를 취해 그들의 차이를 고려하여 엔트로피를 계산하기 때문에 데이터 내재적 원인에 의한 노이즈 영향도 근사 엔트로피에 비해 훨씬 작아진다는 장점이 있다. 보통 샘플 엔트로피에 대해서는 문턱 거리를 \(r = 0.2 \sigma\)로 설정한다. 샘플 엔트로피가 데이터의 복잡도를 정량적으로 잘 측정할 수 있는지 알아 보기 위해 1차원 fBm 데이터를 허스트 지수 \(H\)를 달리하여 수백 번씩 생성시킨 케이스에 대해, 평균 샘플 엔트로피를 구한 결과를 [그림4]에 보였다. 그림에서 볼 수 있듯, 샘플 엔트로피와 \(H\) 사이의 단조감소 경향은 1차원 fBm 데이터의 복잡도가 \(H\) 값에 대해 단조감소 경향을 보일 것이라는 예측과 일치함을 확인할 수 있다.

샘플 엔트로피가 연속 데이터에 대해 적용되었다면 이진 데이터^{binary data}에 특화된 엔트로피 지표도 있다. 1976년 이스라엘의 컴퓨터과학자 에이브러햄 렘펠^{Abraham Lempel}와 제이콥 지브^{Jacob Ziv}가 개발한 ‘램펠-지브 복잡도^{Lempel-Ziv(LZ) complexity}‘ \(C_{LZ}\)가 처음 소개된 이후,[7] 이 복잡도는 텍스트, 이미지, 비디오 등, 각종 디지털 데이터의 용량 압축 알고리즘의 기초 정보로 활용되고 있다. 램펠-지브 복잡도는 이진 데이터의 성분들이 배열된 경우의 수를 계수하여 그룹화시키고, 그룹들이 얼마나 다양하게 분포하고 있는지를 측정함으로써 데이터의 복잡도를 계산한다.

예를 들어 길이 \(N = 4\) 크기의 이진 데이터 \(X = [0 \, 0 \, 1 \, 0]\)를 생각해 보자. 이제부터 할 작업은 이 데이터의 성분들을 일종의 ‘단어^word‘로 간주하여 원본 데이터를 일종의 ‘단어장^vocabulary‘으로 변환하는 것이다. 우선 처음에 나오는 성분인 ‘0’은 ‘단어장’에 등록되지 않았으므로, 이 성분을 가지고 최초의 구획 집합^partition \(W\)를 \(W =\) ‘0’이라고 설정하여 \(X = [0 \,^V \,0 \, 1 \, 0]\) (여기서 \(^V\)는 구획 표시를 의미함)이라고 표현한다. 방금 생성된 구획 집합 바로 다음에 나오는 숫자 조합을 성분으로 갖는 구획 집합을 \(Q\)라고 정의하는데, 우선 가장 짧은 길이, 즉, ‘0’만 고려하여 \(Q =\) ‘0’ 이라고 설정한 후 \(W\)와 \(Q\)를 붙이면 \(WQ =\) ‘0 0’이라는 합성 구획 집합이 생성된다. 여기서 마지막 숫자를 제외한 구획 집합을 \(WQ\pi\)라고 표현한다면 \(WQ\pi=\) ‘0’이 되며, 이제 판단해야 할 것은 \(WQ\pi\)에 \(Q\)가 포함되는지 여부인데, 포함된다면 일단 다음에 구획 표시를 하지 않는다. \(Q = WQ\pi =\) ‘0’이므로 \(Q \in \nu(WQ\pi)\)이며(여기서 \(\nu(T)\)는 구획 집합 \(T\)의 ‘단어장^vocabulary’을 의미함), 따라서 구획 표시를 하지 않는다.

구획 표시를 하지 않는 경우 \(Q\)의 자리 수를 하나 더 늘리는데, 그러면 \(W =\) ‘0’과 \(Q =\) ‘0 1’이 되는 상황이다. 앞의 과정을 다시 거치면, \(WQ =\) ‘0 0 1’이 되고 \(WQ\pi =\) ‘0 0’이므로 \(Q \notin \nu(WQ)\)이 된다. 이렇게 새로 생성된 \(Q\)가 업데이트된 \(WQ\pi\)의 단어장에 포함되지 않았다면, 가장 최근까지의 \(Q\)까지를 구획으로 인정하여 새로운 구획을 정한다. 즉, \(X = [0 \, ^V \, 0 \, 1 \, 0]\)에서 \(X = [0 \, ^V \, 0 \, 1 \, ^V \, 0]\)으로 업데이트된 것이다. 이제 구획이 하나 더 생겼으므로, 가장 최근까지의 구획을 통틀어 \(W\)를 \(W = \) ‘0 1’에서 \(W = ‘0 ^V \, 0 \, 1’\)로 업데이트하고, 위에서 거친 과정을 반복한다. 이제 \(Q = \) ‘0 1’이고 \(WQ = ‘0 \, ^V \, 0 \, 1 \, 0’\)이 되므로 \(WQ\pi= ‘0 \, ^V \, 0 \, 1’\)이며, 따라서 \(Q \in \nu(WQ\pi)\)이므로 \(Q\) 다음에는 구획 표시를 하지 않는다. 그 결과 데이터 \(X = [0 \, ^V \, 0 \, 1 \, ^V \, 0]\)에는 구획이 세 개 생겼으므로 이진 데이터의 LZ 복잡도는 3이 된다. 이 방법을 이용하면 어떤 길이의 이진 데이터라도 구획들의 집합으로 표현할 수 있다. 예를 들어

\[
X = [1 \, 0 \, 1 \, 0 \, 0 \, 1 \, 0 \, 1 \, 0 \, 0 \, 1 \, 0 \, 1 \, 1 \, 1 \, 1 \, 1 \, 0]
\]
은
\[
X = [1 \, ^V \, 0 \, ^V \, 1 \, 0 \, ^V \, 0 \, 1 \, ^V \, 0 \, 1 \, 0 \, ^V \, 0 \, 1 \, 0 \, 1 \, ^V \, 1 \, 1 \, ^V \, 1 \, 1 \, 0]
\]
같은 방법으로 구획 짓기가 가능하므로, 이 경우 1차원 이진 데이터 \(X\)의 렘펠-지브 복잡도는 \(C_{LZ} = 8\)이다. 렘펠-지브 복잡도 지표는 원리상으로 이진 데이터에만 적용할 수 있지만, 연속 데이터도 적절한 처리를 거치면 렘펠-지브 복잡도의 계산 대상이 될 수 있다. 예를 들어 연속 데이터의 이웃한 성분들의 차이를 음과 양의 이진 정보로 표현하거나(즉, 이전 성분도다 크면 1, 작으면 0) 성분들이 전체 평균보다 큰지 여부를 0과 1로 표현하면 이들을 일종의 이진 데이터로 만들 수 있으므로 이에 대한 렘펠-지브 복잡도 측정이 가능하다. 이는 1차원 fBm의 특성 중 일부(예를 들어 자기유사성 여부)를 그들의 차이 간격 벡터인 1차원 fGn^{fractional Gaussian noise}의 허스트 지수와 프랙탈 차원의 관계를 분석하는 방법으로 측정할 수 있는 원리와 비슷하다.

예상할 수 있다시피 LZ 복잡도는 데이터의 크기에 비례한다. 따라서 데이터 크기에 상관 없는 정규화된 복잡도 개념이 필요하며, 이는 LZ 복잡도를 ‘LZ 엔트로피’ \(S_{LZ}\)로 바꾸는 과정에 해당한다. 예를 들어 0과 1이 동일한 비율로 임의의 배열을 이루는 이진 데이터는 이론적으로 복잡도가 최대가 되는데, 그 값은 \(\max(C_{LZ}) = \frac{N}{log_{2} N}\)이다.[7] 따라서 정규화된 LZ 복잡도 \(S_{LZ}\)는

\begin{align}
S_{LZ} = \frac{C_{LZ}}{\max(C_{LZ})} = \frac{C_{LZ}log_{2} N}{N}
\quad \cdots \quad (12)\end{align}

같이 정의될 수 있다. 여기서 추가적으로 고려해야 할 것은 정규화에 활용된 최대 복잡도는 0과 1이 동일한 비율로 있는 경우에만 해당한다는 것이다. 만약 주어진 데이터의 0와 1의 비율이 다르다면 정규화 인자를 바꿔야 한다. 즉, 측정하고자 하는 데이터에 포함된 1의 비율을 \(p\)라고 할 때, \(\max(C_{LZ})\)는

\begin{align}
\max(C_{LZ}) = -\frac{N}{log_{2} N(plog_{2}p) + (1-p)log_{2}(1-p)}
\quad \cdots \quad (13)\end{align}

이 될 것이기 때문에[7] 이를 반영하여 일반적 관점에서 정의되는 \(S_{LZ}\)는

\begin{align}
S_{LZ,corrected} = -\frac{C_{LZ}log_{2}N (plog_{2}p + (1-p)log_{2} (1-p))}{N}
\quad \cdots \quad (14)\end{align}

같이 정의될 수 있다. 흥미롭게도 \(N\)이 충분히 커질 경우, \(C_{LZ}\)는 ‘콜모고로프 복잡도’에 수렴하는데, 이는 \(S_{LZ,corrected}\)가 콜모고로프-시나이 엔트로피^{Kolmogorov-Sinai entropy 혹은 measure entropy}에 수렴할 것임을 의미한다.

예를 들어 허스트 지수 \(H\)에 따라 1차원 fBm 데이터의 변동이 제어되는 경우를 생각해 보자. \(H\)가 증가할수록 fBm은 추세 강화 기조를 보이기 때문에, 이웃한 데이터 성분들 사이의 변동이 점점 감소하여 데이터 복잡도 역시 감소하며, 따라서 엔트로피 감소를 동반한다. fBm의 엔트로피 감소는 fGn의 엔트로피 감소를 동반하기 때문에, fGn의 이진화된 버전의 데이터에 대해 엔트로피를 측정하는 LZ 엔트로피 역시 \(H\)에 대해 단조감소 경향을 보일 것임을 예측할 수 있다. 실제로 [그림5]에서 볼 수 있듯 1차원 fBm에 대해, \(S_{LZ}\)가 허스트 지수 \(H\)에 대해 단조감소 경향을 보임을 확인할 수 있다. LZ 엔트로피는 샘플 엔트로피와 달리 범위가 0에서 1 사이이기 때문에 적어도 이진 데이터에 대해서라면 더 직관적인 정보량 혹은 복잡도 지표가 될 수 있다.

지금까지 알아 본 근사, 샘플, LZ 엔트로피 등은 데이터의 성분들의 ‘순서’에 대한 고려는 없었다. 즉 \(X = [4 \, 5 \, 1 \, 2 \, 3]\)과 \(Y = [1 \, 2 \, 3 \, 4 \, 5]\)의 복잡도 구분이 되지 않았던 것이다. 만약 데이터 성분의 크기에 따른 순서에도 의미를 부여해야 하는 상황이라면 이를 감안한 복잡도를 어떻게 측정할 수 있을까? 이를 위해서는 결국 원본 데이터에서 추출한 샘플 데이터 내부의 성분들 사이의 ‘순서’에 대한 고민이 있어야 한다. 이를 고려한 엔트로피를 ‘순열 엔트로피^{permutation entropy}‘라고 한다.[8] 순열 엔트로피를 이해하기 위해서는 ‘순열 패턴^{ordinal pattern}‘이라는 개념을 먼저 알아야 한다.

순열 패턴을 어떻게 계수할 수 있을까? 먼저 주어진 1차원 데이터 \(X = [x(1) \, x(2) \, … \, x(N)]\)에서 일부 데이터를 샘플링하기 위해 순서 수^{order number} \(d\)와 지연 간격^delay \(\tau\)를 설정한다. 여기서 순서 수란 샘플링하는 데이터의 크기보다 하나 작은 수를 의미하며, 지연 간격이란 샘플링할 때 성분 간 간격을 몇 번 건너 뛸 것인지를 의미한다. 예를 들어 \(N=11\)의 데이터 \(X=[1 \, 10 \, 6 \, 5 \, 4 \,8 \, 9 \, 2 \, 5 \, 3 \, 7]\)가 주어졌을 때 \(d=2\), \(\tau=2\)라고 설정한다면 샘플링은 \(d+1=3\)성분씩, 간격은 \(\tau=2\)을 유지하며 샘플링된 벡터들(이것을 \(X_{i}^{\tau} = [x(i) x(i+\tau) … x(i+d\tau)]\)라고 정의함)은 \(X_{1}^{2} = [1 \, 6 \, 4]\), \(X_{2}^{2} = [10 \, 5 \, 8]\), \(X_{3}^{2} = [6 \, 4 \, 9]\), \(X_{4}^{2} = [5 \, 8 \, 2]\) 등이 된다. 샘플링된 벡터들은 공통적으로 성분이 \(d+1=3\)개씩 있지만, 각 성분들 사이의 크기에 따른 순서는 제각각인데 이 순서를 서로 구분되는 벡터로 만들 수 있다. 예를 들어 \([1 \, 6 \, 4]\) 같은 벡터는 성분의 절대값을 서열의 기준으로 고려한다면 \([1st \, 3rd \, 2nd]\) = [1 \, 3 \, 2]\)이 되고, \([10 \, 5 \, 8]\) 같은 벡터는 \([3rd \, 1st \, 2nd] = [3 \, 1 \, 2 ]\)로 표현할 수 있다.

물론 절대값만 서열의 기준이 될 필요는 없다. 데이터 성분이 숫자가 아닌 텍스트라면 사전에 정한 텍스트 성분의 순서값이 서열을 매기는 기준이 될 수 있다. 이러한 순서 벡터를 ‘순열 패턴’이라고 한다. 예로 들고 있는 샘플 데이터의 경우 성분이 세 개 있으므로 가능한 순열 패턴은 총 \((d+1)! = 6\)개가 나온다. 나아가 각 순열 패턴마다 고유의 ‘코드’를 배정하면 나중에 분류하고 이들의 출현 빈도를 계수할 때 매우 편리하다. 이를 위해 ‘반전수^{inversion number}‘라는 숫자 벡터 \(i_{inv} = [i_{1} \, i_{2} \,… \,i_{d}]\)를 도입하면 편리하다. 예를 들어 \(d=2\)인 경우의 반전수 벡터는 \(i_{inv} = [i_1 \, i_2]\)이 된다. 샘플링된 데이터 \(X^{\tau}\)에 대해 반전수 벡터의 성분은

\(i_l = number \, of \, {r \in {0,1,…,l-1}\mid x(t+(d-l)\tau) \geq x(t+(d-r)\tau)}, \, l=1,2,…,d\)

의 규칙으로 정한다. 예를 들어 샘플링된 벡터 \(X_1^{(2)} = [1 \, 6 \, 4]\)에 대해 순열 패턴은 \([1 \, 3 \, 2]\)이 될 것이고, \(i_1\)의 경우 \(r=0\)인 경우만 고려하면 되는데, 이때 \(x(t+\tau) \geq x(t+2\tau)\)의 부등식 관계가 성립하는지를 판단해야 한다.

\(X_1^{(2)} = [1 \, 6 \, 4]\)에 대해 \(x(t)=1\), \(x(t+\tau) = 6\), \(x(t+2\tau)=4\)이므로 부등식 \(x(t+\tau) \geq x(t+2\tau)\)이 만족되고, 따라서 \(i_1=1\)이다. \(i_2\)의 경우, \(r=0\), \(r=1\) 두 가지 가능성을 고려해야 하는데, 먼저 \(r=0\)인 경우 \(X_1^{(2)} = [1 \, 6 \, 4]\)에 대해 부등식 \(x(t) \geq x(t+2\tau)\)은 \(x(t) \leq x(t+2\tau)\)이므로 성립하지 않고, 따라서 빈도가 계수되지 않는다. \(r=1\)인 경우 부등식 \(x(t) \geq x(t+\tau)\)은 \(x(t) < x(t+\tau)\)이므로 역시 성립하지 않고 따라서 빈도가 계수되지 않는다. 즉, \(i_2 = 0\)이 된다. 비슷한 방식으로 \(X_2^{(2)} = [10 \, 5 \, 8]\)은 순열 패턴이 \([3 \, 1 \, 2]\)고, 이 패턴에 대해서 \(i_1\)과 \(i_2\)를 계산하면 \(i_1 = 0\)과 \(i_2 = 2\)라는 것을 발견할 수 있다. 따라서 순서수 \(d=2\)에 대해 나올 수 있는 여섯 가지(\((d+1)!=6\))의 모든 순열 패턴은 [그림6]에 보인 것 같이 고유의 반전수쌍으로 다시 표현이 가능하다.

반전수가 주어지면 순열 패턴의 코드화도 가능하다. 예를 들어
\[
n_{d} (i_1,\,i_2,\,…,\,i_d) = \sum_{u=1}^{d} i_l \frac{(d+1)!}{(l+1)!}
\]
의 관계식을 이용하면 고유 코드가 만들어진다. 위에서 살펴본 \(d=2\)의 사례에서는 [그림6]처럼 \(n_{2} (i_1,i_2) = 0,1,…,5\)의 고유 코드 6개가 각 순열 패턴에 대해 배정될 수 있다. 순열 패턴을 이용하면 주어진 데이터의 복잡도를 측정할 수 있는 정교한 도구가 생성되는데, 이를 위해 추출 크기(이를 창^window크기 \(W\)라고 한다)를 설정한다. 예를 들어 [그림7]에 보인 경우는 \(W=9\)이다. 이때 창 크기는 \(5(d+1)! < W\)의 조건을 만족하게끔 설정한다.[9]

창 크기 \(W\)는 전체 데이터 크기의 절반 정도로 잡으면 충분하다고 알려져 있다. 창 크기가 정해지면 샘플 데이터를 추출할 수 있으며 총 \(M = W – (d\tau)\)개의 순열 패턴이 나온다. 또한 위에서 소개한 순열 패턴의 고유 코드를 이용하면 첫 번째 창의 순열 패턴은 \([4 \, 4 \, 1 \, 2 \, 3]\) 같은 코드 벡터로 표현될 수 있고, 두 번째 창의 순열 패턴은 \([4 \, 1 \, 2 \, 3 \, 0]\) 같은 코드 벡터로 표현될 수 있다. 이렇게 생성된 \(k\)번째 창의 순열 패턴의 고유 코드 벡터에서 각 고유 코드 \(p\)의 출현 빈도 \(q_{p} (k)\)를 계수할 수 있다. 예를 들어 첫 번째 창에 대해서는 \([q_{0} (1) \, q_{1} (1) \, q_{2} (1) \, q_{3} (1) \, q_{4} (1) \, q_{5} (1)] = [0 \, 1 \, 1 \, 1 \, 2 \, 0]\)이고, 두 번째 창에 대해서는 \([q_{0} (2) \, q_{1} (2) \, q_{2} (2) \, q_{3} (2) \, q_{4} (2) \, q_{5} (2)] = [1 \, 1 \, 1 \, 1 \, 1 \, 0]\)이 될 것이다. 이를 이용하여 (정규화된) 순열 엔트로피 \(ePE\)를 다음과 같이 정의할 수 있다.

\begin{align}
ePE(d,\tau,M,t) = \frac{S(d,\tau,M,t)}{S_{\max}} = \frac{-\sum_{j=0}^{(d+1)!-1} \frac{q_{j}(t)}{M} log(\frac{q_{j}(t)}{M})}{-\frac{(d+1)!}{M}log(\frac{1}{M})}
\quad \cdots \quad (15)\end{align}

위 식에서 분모에 있는 \(S_{\max} = -\frac{(d+1)!}{M} log(\frac{1}{M})\)는 최대 엔트로피로, \(q_{j}(t)=1\)인 경우의 엔트로피를 의미한다. 이를 이용하여 위에서 예로 든 각 추출 데이터에 대해 \(ePE(2,2,5,1) = 0.6898\), \(ePE(2,2,5,2) = 0.8333\)라는 결과를 얻을 수 있다.

순열 엔트로피가 계의 복잡도 혹은 프랙탈 차원과 어떻게 연관되는지 이해해 보기 위해 1차원 fBm의 경우를 예로 들어 보자. 허스트 지수 \(H\)가 증가할수록 1차원 fBm의 프랙탈 차원은 점점 1차원으로 수렴한다. 그와 동시에 계의 엔트로피 역시 감소할 것인데, 실제로 [그림8]처럼 \(H \leq 0.5\)까지는 완만하게 순열 엔트로피가 감소하다 \(H \geq 0.8\)부터는 급격하게 감소하는 것을 확인할 수 있다. 또한 그림에서 볼 수 있다시피 샘플링 크기가 커질수록 엔트로피가 조금씩 감속하는 경향을 보인다.

순열 엔트로피 역시 샘플링 간격, 즉, \(\tau\)가 커질수록 측정되는 복잡도도 같이 증가하는 경향과 일정 수준 이상의 노이즈에 영향을 많이 받는 경향을 보인다. 이를 보정할 필요가 있으며 방법 중 하나가 ‘조건부 순열 엔트로피^{empirical conditional permutation entropy or empirical conditional entropy, \(eCPE(d,\tau,M,t)\)}‘라 부르는 방법이다. 이 방법은 순열 엔트로피에서 도입한 delay의 영향을 자체적으로 제거하기 위해, delay가 한 번 더 진행된 데이터 벡터와 그렇지 않은 벡터의 상호관계를 고려하여 엔트로피를 계산한다. 예를 들어 \(eCPE(d,\tau,M,t)\)는

\begin{align}
eCPE(d,\tau,M,t) = -\sum_{j=0}^{(d+1)!-1} \sum_{j=0}^{(d+1)!-1} \frac{q_{j} (t)}{M} \frac{p_{j,l} (t)}{q_{l} (t)}
\quad \cdots \quad (16)\end{align}

같이 표현할 수 있는데, 위 관계식에서 \(p_{j,l}\)는 정해진 크기의 샘플 데이터 \(X_{t}^{\tau} = [x(t) x(t+\tau) … x(t+d\tau)]\)에 대해 \(X_{t}^{\tau}\)의 순열 패턴 고유 숫자가 \(j\)이며 \(\tau\)만큼 평행 이동시킨 또 다른 샘플 데이터 \(X_{t+\tau}^{\tau} = [x(t+\tau) x(t+2\tau) … x(t+d\tau + \tau)]\)에 대해 \(X_{t+\tau}^{\tau}\)의 순열 패턴 고유 숫자가 \(l\)인 조합의 개수를 의미한다. \(W\)가 충분히 크다면 \(X_{t}^{\tau}\)와 \(X_{t+\tau}^{\tau}\)의 순열 패턴 복잡도는 큰 차이가 없을 것이므로 \(\tau\)의 영향은 그만큼 줄어들 것이고 이를 고려하는 조건부 순열 엔트로피는 원래의 순열 엔트로피에 비해 \(\tau\)의 영향을 덜 받을 것이다. 따라서 그만큼 데이터 복잡도를 측정하는 정확도가 더 높아진다.

[그림9]에는 로지스틱 사상^{logistic map} \(x_{n+1} = rx_{n}(1-x_{n})\)에서 생성된 1차원 데이터 \(X = [x_{1} \, x_{2} \, … \, x_{N}]\)에 대해 파라미터 \(r\)이 증가함에 따라 변하는 랴푸노프 지수^{Lyapunov exponent}, 허스트 지수(DFA 방법으로 계산), 샘플 엔트로피(\(m=2\)인 경우), LZ 엔트로피, 순열 엔트로피(\(\tau=1\), \(W=2^{10}\), \(d=4\)인 경우), 조건부 순열 엔트로피(\(\tau=1\), \(W = 2^{10}\), \(d=4\)인 경우)를 계산하여 비교하였다.

[그림9]에서 확인할 수 있듯, 전반적으로 랴푸노프 지수로 대표되는 이론적인 데이터 복잡도를 제일 잘 추적하고 있는 지표는 샘플 엔트로피이며, 순열 조건부 엔트로피 역시 계의 복잡도를 정량적으로 잘 측정하고 있는 것을 확인할 수 있다. 로지스틱 사상은 각종 복잡도 지표들 간의 비교를 위해 활용한 예일 뿐이고, 실제 데이터(예를 들어, 주가 지수, EEG 같은 생체 신호의 시계열 데이터 등)의 복잡도 분석에는 다양한 지표를 종합적으로 살펴 볼 필요가 있다. 특히 다루려고 하는 데이터에 특정한 주기나 자기닮음꼴, 프랙탈 특성 등이 나타날 것이라 예상한다면 이러한 지표들을 상호 비교하여 그 특성을 정확히 가려내는 것이 중요하다.

2차원 패턴의 엔트로피 계산

앞서 살펴보았던 다양한 종류의 엔트로피는 주로 1차원 데이터를 고려하여 알고리즘을 설계했다. 당연히 이러한 알고리즘은2차원 이상의 고차원 데이터에 대해서도 확장 적용이 가능하다. 2차원 이상의 데이터와 1차원 데이터의 가장 큰 차이점은 차원이 확장되었기 때문에 원본 데이터에서 샘플 데이터를 추출할 때 고려해야 할 데이터 성분의 ‘방향성’이 생긴다는 것이다. 수치해석적인 관점에서 보았을 때 2차원 이상의 데이터가 확장된 차원을 갖는다는 것은 그만큼 계산량이 기하급수적으로 증가함을 의미하는 것이기도 하다.

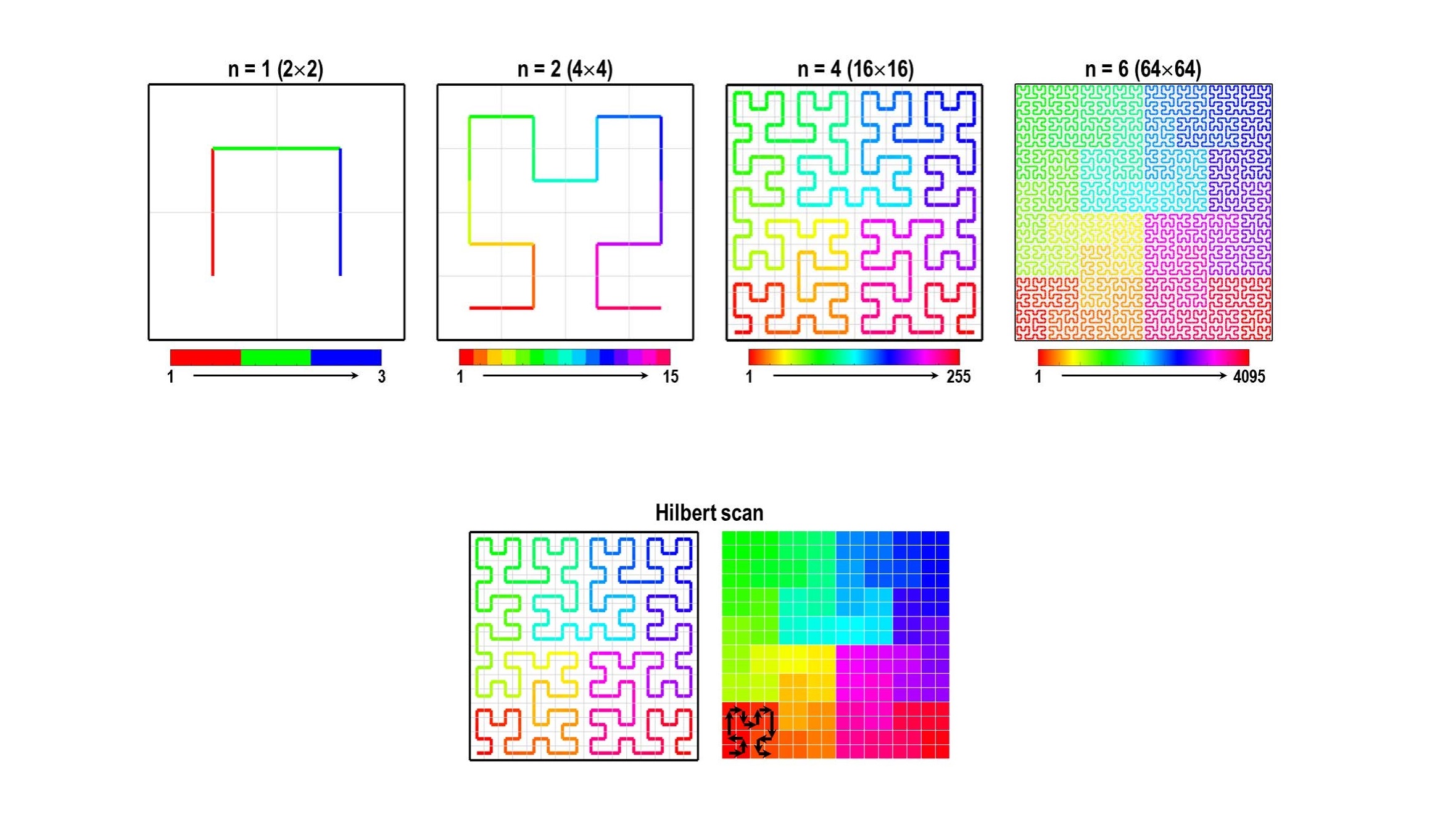
이를 우회할 수 있는 방법 중 하나는 바로 “패턴의 과학 [1]: 패턴의 자기닮은꼴과 프랙탈 차원”에서 잠깐 살펴본 ‘공간충전곡선^{space-filling curves}‘을 이용하는 것이다. 예를 들어 [그림10]처럼 힐베르트 곡선^{Hilbert curve}를 이용하면 2차원 이상의 이산 공간을 자기닮음꼴 성질이 내재된 한붓그리기 방식으로 채워 나갈 수 있는데, 이 곡선을 주욱 잡아당긴다고 생각한다면 2차원 이산 공간은 결국 1차원의 끈, 즉, 1차원 벡터 형식의 데이터로 차원이 축소될 것이다.

[그림11]은 2차원 힐베르트 곡선을 이용하여 2차 정방행렬의 모든 성분을 어떻게 한 번씩 방문하면서도 각 성분들이 주변의 이웃 성분에 대해 거의 같은 이웃 개수를 유지할 수 있는지를 보여준다. 원리적으로는 힐베르트 커브 같은 공간충전곡선이 완벽한 자기닮음꼴을 유지해야 하는 상황에서라면 2차원 이상의 공간의 크기는 아무 크기가 될 수는 없다. 즉, 한 차원의 크기가 \(2^{m}, m \in \mathbb{N}\)이 되는 경우만 허용이 되는 것이다.

그렇지만 이 역시 우회할 수 있는 방법이 있는데, 주어진 차원의 데이터의 각 방향의 성분 개수를 2진수로 나타내어, 일종의 쪽거리 붙이기 등의 방법을 반복하여 힐버트 곡선의 자기유사성을 거의 이상적으로 유지한 채 공간을 채울 수 있다.[10] 이는 2차원뿐만 아니라 3차원, 나아가 4차원 이상의 하이퍼큐브 공간에서도 적용이 가능하다. 이제 고차원 데이터도 1차원으로 차원을 축소할 수 있는 방법이 생겼기 때문에 앞서 살펴보았던 1차원 데이터의 엔트로피 분석을 그대로 적용할 수 있다.

2차원 데이터의 엔트로피를 공간충전곡선으로 차원 축소하여 측정할 수 있는지는 다양한 방법으로 생성되는 패턴의 복잡도 측정으로 테스트해 볼 수 있다. 통계물리 분야에서 2차원 시스템의 상전이 모형^{phase transition model}으로 자주 활용되는 ‘2차원 이징 모형^{2D Ising model}‘이나 ‘2차원 XY 모형^{2D XY model}‘은 외부에서 가해 주는 열 에너지나 자기장 세기 등의 조건에 따라, 시스템이 완전히 무질서한 상태^{disordered state}에서 질서있는 상태^{ordered state}로 상전이를 보이는 시스템이다. 

2차원 이징 모형의 경우 온도 변화에 따라 스핀^spin이 뒤집힐 확률을 계산할 수 있고, 각 온도 조건에 대해 스핀의 방향이 오랜 시간이 흐른 후 방향이 어떻게 분포하는지를 몬테카를로 방법 등으로 시뮬레이션^{Monte-Carlo simulation} 할 수 있다. 평형 상태에서 바둑판 모양의 격자로 배치된 수많은 스핀들은 특정한 확률적 분포로 인해 2차원 이진 패턴^{2D binary pattern}을 이루게 되며, 스핀들이 위치한 행렬 성분을 힐베르트 곡선 등으로 차원 축소하여 1차원 벡터로 전환한 후에는 그 벡터의 LZ 엔트로피나 샘플 엔트로피, 순열 엔트로피 등으로 패턴의 복잡도를 측정할 수 있다. [그림12]는 그 결과를 보여준다.

그림에서 볼 수 있다시피 외부 자기장이 가해지지 않은 상태에서 시스템은 오로지 온도 (\(T\)) 변화에 의해서만 상전이를 겪게 되는데, 이론에 따르면 상의 특성이 확연히 바뀌는 전이 온도^{critical temperature, \(T_{C}\)} 전후에서 스핀 배열 이진 패턴의 엔트로피도 확연한 변화를 보여야 한다. 실제로 엔트로피가 변하는 양상은 샘플 엔트로피나 순열 엔트로피로 측정했을 경우. 공히 이론적으로 예측되는 특성과 잘 일치하는 것을 확인할 수 있다. 2차원 XY 모형의 경우 스핀의 배향은 두 방향으로 한정되지 않고, 0부터 360도까지 연속적으로 변할 수 있기 때문에 이들이 배열되는 2차원 패턴의 엔트로피 계산은 LZ 엔트로피보다는 샘플 혹은 순열 엔트로피로 측정하는 것이 적절하다.

[그림13]에는 2차원 XY 모형의 스핀 배향 각도 분포를 몬테카를로 시뮬레이션한 결과에서 얻어진 패턴의 복잡도를 측정하기 위해, 2차원 스핀 패턴의 차원을 축소한 후 샘플 및 순열 엔트로피로 복잡도를 계산한 결과를 온도에 따른 함수로 보였다.[11] 그림에서 확인할 수 있다시피 몬테카를로 방법으로 추적한 시스템의 엔트로피와 샘플 엔트로피로 계산한 값이 잘 일치하는 것을 확인할 수 있다.

주목할만한 부분은 2차원 이징 모형과는 달리 2차원 XY 모형 같은 연속 패턴에서는 순열 엔트로피보다 샘플 엔트로피가 훨씬 더 정확한 복잡도 지표가 될 수 있다는 것이다. 2차원 이징 모형 같은 이진 패턴에서는 1과 0 사이에 중간 값을 인정하지 않기 때문에, 순열 패턴이 주는 추가적인 정보량은 샘플 크기에 함몰되어 결과적으로 순열 엔트로피와 샘플 엔트로피는 같은 값을 보인다.

그러나 2차원 XY 모형 같은 연속 패턴에서는 다양한 값의 분포가 ‘순서’에 의미를 부여하기 때문에, 순열 엔트로피와 샘플 엔트로피는 서로 다른 값을 갖게 된다. 특히 2차원 XY모형 같은 경우 개별 스핀이 다른 이웃 스핀에 대해 상대적으로 어떻게 배향되었는지의 각도 분포 계산 과정에 이미 경우의 수에 대한 계수가 들어가기 때문에, 이 상태에서 순서 변화에 의한 추가적인 정보량을 반영할 경우, 엔트로피는 원래의 값보다 더 증가하게 된다. 따라서 [그림13]에서 보인 것 같이 샘플 엔트로피에 비해 순열 엔트로피가 더 높게 측정되는 것이며, 이는 이론적인 값보다 더 크게 측정되는 결과를 야기한다. 따라서 성분의 상대적인 순서 배열이 중요한 의미를 갖는 경우를 제외하고서는 샘플 엔트로피로 패턴의 복잡도를 측정하는 것이 일반적으로 적용될 수 있다.

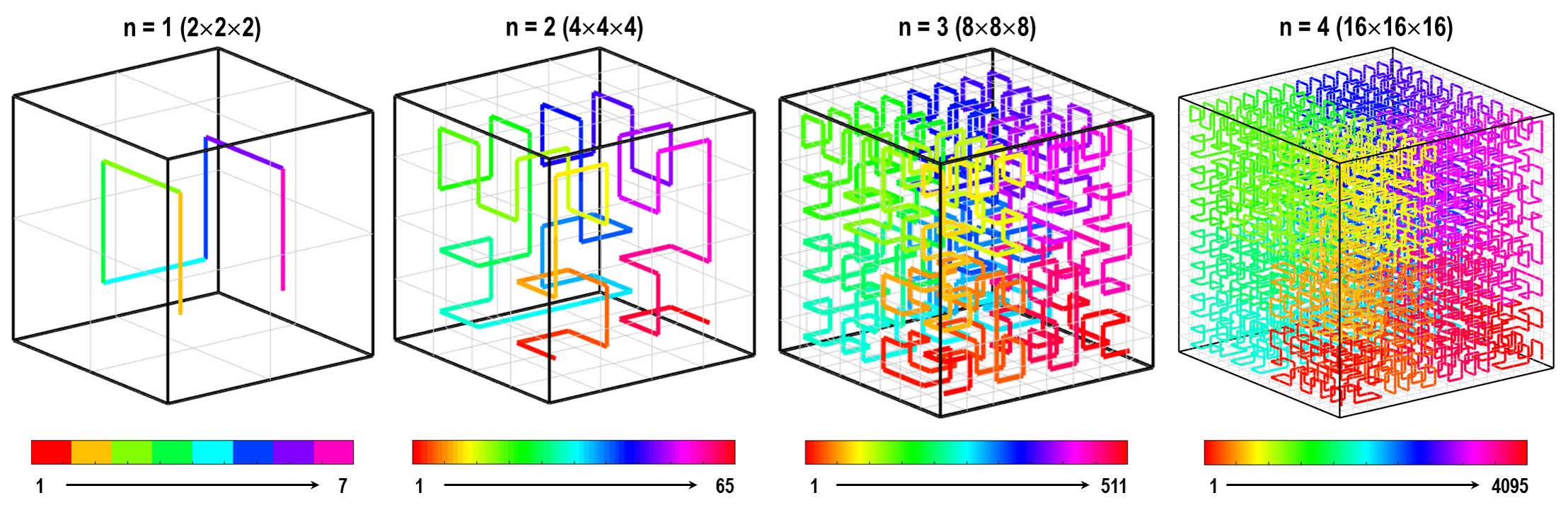
2차원 패턴뿐만 아니라 3차원 패턴의 엔트로피 역시 비슷한 방법으로 계산할 수 있다. 왜냐하면 공간충전곡선은 2차원뿐만 아니라 3차원 공간, 그리고 4차원 이상의 하이퍼큐브 공간도 자기닮음꼴을 유지한 채 한붓그리기로 채우는 것이 원리적으로 가능하기 때문이다. 예를 들어 [그림14]은 다양한 크기를 갖는 3차원 정육면체 행렬의 각 성분을 힐베르트 곡선으로 어떻게 채울 수 있는지를 보여준다.

이미 이론적으로 탐색된 결과와 비교할 수 있는 대표적인 사례로, ‘3차원 퍼콜레이션 네트워크^{3D percolation network}‘의 상전이 현상에서 보이는 패턴의 엔트로피 변화가 상전이 온도 전후에 어떠한 양상을 보이는지 살펴보자. [그림15]처럼 ‘지점 퍼콜레이션 모형^{site-percolation model}‘에 기반하여, 몬테카를로 방법으로 시뮬레이션한 3차원 퍼콜레이션 네트워크는 지점들의 연결도를 기준으로 클러스터^{cluster, 바둑의 대마처럼 하나의 덩어리로 연결된 지점들의 모임}들의 모임으로 다시 표현할 수 있다. 즉, 큐브 격자 내의 각 점들이 연결된 모임을 구분하여 그 모임을 하나의 클러스터로 정하고, 서로 다른 클러스터는 서로 다른 색으로 표시하면, 그 결과는 그림처럼 알록달록한 3차원 큐브 형태의 패턴이 된다.[11]

참고로 큐브가 알록달록할수록 클러스터들의 크기가 작고 따라서 하나의 클러스터로 연결되었을 (즉, 퍼콜레이션을 이루었을) 확률이 낮다는 것을 의미한다. 3차원 퍼콜레이션 네트워크 모형에서는 지점 연결 확률^{site-connection probability} \(P_{site}\)를 조절하면, 비교적 낮은 \(P_{site}\) 값의 조건에서는 클러스터들이 하나로 연결될 확률이 매우 낮지만, 점점 \(P_{site}\) 값이 증가할 경우 클러스터들이 하나로 연결되어 결국 퍼콜레이션^percolation을 이루는 상전이를 겪게 된다. 따라서 임계 확률에 해당하는 \(P_{site,C}\) 즉, 상전이 지점을 찾을 수 있다.

통계물리학 이론에서 잘 알려진대로 2차원 이상의 퍼콜레이션 모형은 대표적인 ‘2차 상전이 시스템^{second-order phase transition}‘으로, 상전이 지점 전후로 엔트로피의 변화가 연속이면서 미분 가능하다는 특성을 보인다. [그림15]의 오른쪽 그래프와 같이, 지점 연결 확률이 주어졌을 때, 생성된 3차원 퍼콜레이션 네트워크 클러스터 패턴을 힐베르트 곡선을 이용하여 차원 축소한 후, 시스템의 엔트로피를 샘플 엔트로피로 측정한 결과도 이러한 2차 상전이 특성을 잘 보여 주고 있다.[11]

2차원 패턴의 배치 엔트로피 계산

앞서 힐베르트 곡선에 기반한 차원 축소 방법으로 2차원 이상의 고차원 패턴 복잡도를 샘플 엔트로피 등의 계산을 통해 구하는 방법을 알아보았다. 하지만 차원 축소 방법이 적용될 수 없는 경우는 어떻게 복잡도를 계산해야 할까? 즉, 2차원 이상의 행렬로 표현될 수 없는 형태의 패턴의 복잡도를 어떻게 정량화할 수 있을까?

이런 사례의 대표적인 경우로서 입자들이 자기조립된 시스템의 복잡도를 계산하는 경우를 생각할 수 있다. 예를 들어 반데르발스 인력^{van der Waals attraction}과 탄성력에 의한 척력이 균형을 이루어 매우 작은 입자들(10nm보다 작은 크기의 나노입자)이 자기들끼리 적당한 간격을 두고 좁은 영역에서 뭉치는 현상인 ‘자기조립^{self-assembly}‘은 두 힘의 균형 범위가 어디까지인지, 나노입자의 형태는 어떤지, 표면에너지는 얼마나 큰지, 탄성력을 지배하는 나노입자 바깥층의 상태는 어떤지 등의 여러 요소들의 조합에 따라 같은 자기조립이더라도 질서도에 차이가 날 수 있다. 완벽하게 육각대칭구조로 빽빽하게 채워진 구조^{hexagonal close packed structure, 이른바 ‘2차원 고체’}부터 적절하게 무질서도가 가미되어 불규칙하게 채워진 구조^{disordered assembly structure, 이른바 ‘2차원 액체’}까지, 질서도가 조금씩 무너지면서 입자들은 여전히 자기조립된 상태를 유지할 수 있다.

이러한 입자들의 배열이 이루는 복잡도 측정은 자기조립이 2차원에서 이루어질 경우, 이전처럼 차원 축소법에 의거한 샘플 엔트로피 계산으로는 정확한 값을 산출할 수 없다. 그 이유는 앞서 살펴본 이미지들이 행렬로 표현할 수 있는 연속 이미지였던 반면, 나노입자의 자기조립 같은 케이스는 나노입자가 있는 영역과 없는 영역의 ‘모 아니면 도’ 식의 기하학적 구분과 더불어, 개별 나노입자 주변에 가까운 이웃 나노입자가 몇 개나 들어차 있는지에 대한 위상수학적 고민도 필요하다. 따라서 개별 나노입자를 기준으로 이웃한 나노입자의 ‘상대적 배치’의 경우의 수를 고려한 새로운 엔트로피 접근 방법이 필요하기 때문이다. 이를 ‘배치 엔트로피^{configuration or configurational entropy}‘라고 한다.[12]

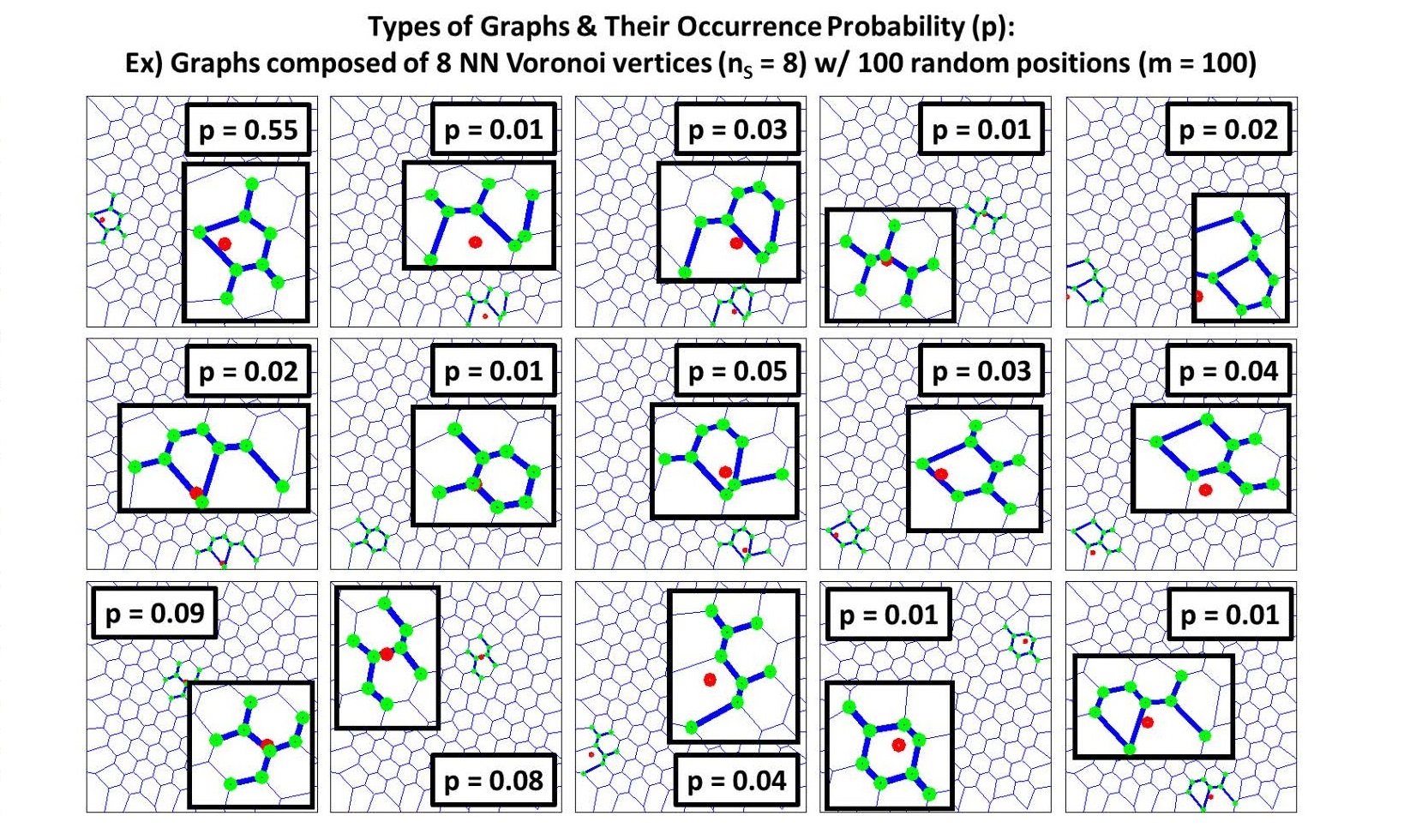
배치 엔트로피 계산의 시작은 개별 입자들의 위치를 파악하여 이들의 연결도를 하나의 ‘그래프^graph‘로 표현하는 것이다. 이를 위해 일단 개별 입자의 중심점^coordinate을 2차원 평면 상에 표시하고 각 입자의 중심점을 기준으로 이들이 차지하는 최적의 비겹침 영역을 계산한다. 이러한 계산은 ‘보로노이 조각화^{Voronoi tessellation}‘라는 방법으로 가능하다. 간단히 이야기하면 이 방법은 각 중심점을 이은 선분의 수직 이등분선(3차원이라면 이등분면)으로 둘러싸인 다각형^polygon(3차원이라면 다면체^polytope) 형태의 영역을 찾는 것이다. 보로노이 조각화가 끝나면 [그림16]처럼 벌집 모양을 닮은 조각화된 그래프가 만들어진다.

이제 다음에 할 일은 이 그래프가 놓인 평면 상에 임의로 한 점을 찍고(빨간색 점), 정해진 개수(\(n_{S}\))만큼의 ‘최단 거리 이웃’이 될 그래프들의 꼭지점(초록색 점)들을 찾은 후, 이 점들로만 이루어질 수 있는 그래프 상의 고유 연결 형태를 찾는 것이다. 이러한 고유 연결 형태가 얼마나 자주 출현할지를 계산하기 위해 평면 상에서 임의의 점을 수백-수천 번 시험하여 고유 연결 형태들을 분류하고(이를 ‘그래프 동형사상^{graph isomorphism}‘이라고 한다) 통계적인 확률 분포를 계산한다.

예를 들어 [그림17]은 \(n_{S} = 8\)인 경우에 대해 서로 다른 고유 연결 형태의 출현 확률을 계산한 결과를 보여준다. 주어진 \(n_{S}\)에 대해 고유 연결 형태가 총 \(N_{g}\)개 관측되었다고 할 때, 각 형태의 출현 확률 \(p_{i} (n_{S}), \, i=1,\,2\,…\,N_{g}\)를 이용하면 이들의 정보 엔트로피 \(S(n_{S})\)를 다음과 같이 계산할 수 있다.

\begin{align}
S(n_{S}) = -k_{B}\Sigma_{i=1}^{N_{g}} p_{i}(n_{S}) logp_{i}(n_{S})
\quad \cdots \quad (17)\end{align}

이때 \(S(n_{S})\)의 계산은 제한된 영역에서 점을 임의로 골라내어 고유 형태를 찾는 것에 의존하고 있으므로 제한된 영역의 효과를 수정하기 위해 수정된 정보 엔트로피 \(S_{C}(n_{S})\)를 다음과 같이 계산한다.

\begin{align}
S_{C}(n_{S}) = S(n_{S}) – k_{B}logn_{S}
\quad \cdots \quad (18)\end{align}

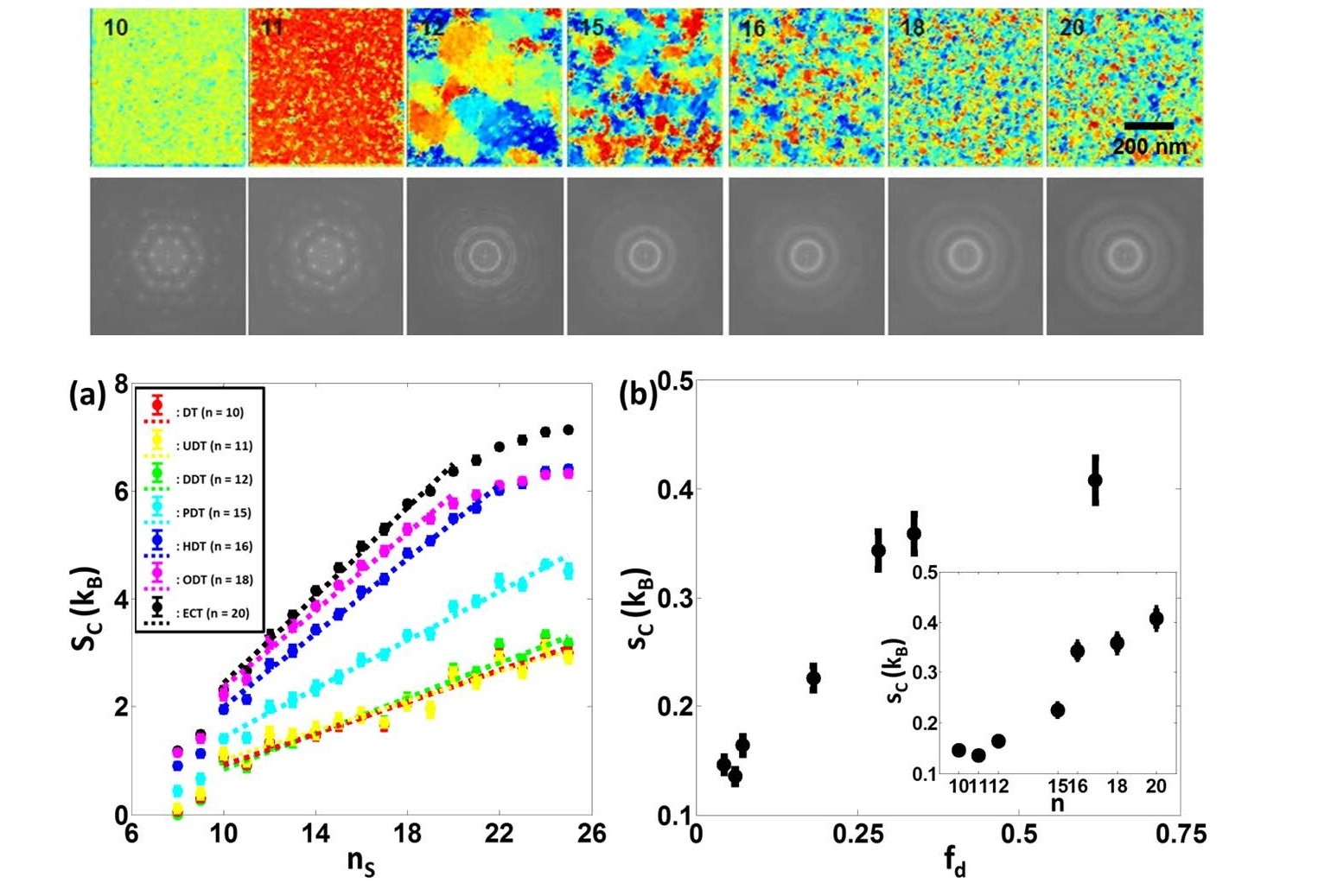
마지막으로 단위 입자 당 엔트로피를 계산하기 위해 \(S_{C}(n_{S})\)과 \(n_{S}\)의 관계를 분석하여, 이들이 선형 관계를 이루는 영역에 대해 선형성의 기울기를 구한다. 이 기울기를 자기조립 시스템의 단위 입자 당 배치 엔트로피 \(s_{C}\)로 정의한다. 이 방법을 이용하여 [그림18]처럼, 금 나노입자^{Au nanoparticles}가 특정한 유기물(예를 들어 alkanethiol 같은 유기분자)로 둘러싸여 있을 때, 자기들끼리 조립되어 2차원 구조체를 이루는 자기조립 패턴의 배치 엔트로피를 계산할 수 있다.[13]

이러한 배치 엔트로피는 여러 조건에서 자기조립 구조체의 질서도가 제어된 경우, 각 샘플의 엔트로피를 알려 줄 수 있기 때문에, 자기조립 구조체가 어떻게 상전이를 겪으며 상전이의 특성이 어떤지에 대해 많은 정보를 줄 수 있다.

예를 들어 [그림19]처럼 금 나노입자를 둘러싸고 있는 유기물의 분자량이 커질수록 유기분자들 간의 섭동^perturbation 영향이 커져서, 나노입자들의 자기조립 과정에 결함^defect이 누적되고, 이는 자기조립 구조체의 질서도가 무너지는 것으로 발현된다. 이러한 질서도 무너짐 현상은 통계물리학에서는 전형적인 ‘2차원 녹음 현상 ^{2D melting}‘에 해당하는 상전이 현상이다.[13] 이러한 상전이는 [그림19]처럼 배치 엔트로피의 계산을 통해 엔트로피와 엔트로피 미분값이 상전이 지점에서 연속성을 가지므로 ‘2차 상전이^{2nd order phase transition}‘임을 알 수 있다.[13]

배치 엔트로피를 상전이 특성 해석에 적용한 사례에서도 볼 수 있듯, 단순한 기하학적 원리에 의해 생성된 2차원 패턴뿐만 아니라 위상수학적으로 구성 성분 사이의 연결도^connectivity를 고려하는 2차원 패턴에 대해서도 엔트로피를 계산할 수 있으며 이를 통해 더 다양한 종류의 시스템의 복잡도, 나아가 시스템의 열역학적인 특성 같은 물리적 특성과 정보량에 대한 분석도 가능함을 확인할 수 있다.

맺는말

지금까지 패턴의 복잡도와 정보량을 엔트로피 관점에서 어떻게 측정할 수 있을지 다양한 접근 방법과 원리, 그리고 측정된 결과의 특성에 대한 내용을 여러 사례와 함께 소개하였다.

기본적으로 패턴은 2차원 이상의 고차원 데이터지만, 패턴이 행렬 형태로 표현될 수 있다면 차원 축소 방법을 이용하여 1차원 벡터로 변환하고 그 벡터의 정보량은 근사, 샘플, LZ, 순열 엔트로피 등으로 계산할 수 있음을 보였다. 또한 행렬 형태로 바꿀 수 없는 패턴은 위상수학적 관점에서 그래프로 변환하여 배치 엔트로피 같은 그래프-기반 엔트로피 계산 방법으로 분석할 수 있음을 보였다. 2차원뿐만 아니라 3차원 형태의 패턴 역시 이들이 행렬 형태로 표현될 경우(이 경우 voxel data라고 부른다) 마찬가지로 공간충전곡선을 이용하여 차원 축소한 후 샘플 엔트로피 등을 계산할 수 있으며, 행렬 형태로 표현될 수 없을 경우도 고유 연결 형태의 정보 엔트로피를 계산함으로써 복잡도와 정보량을 계산할 수 있다.

2차원 이상 패턴의 복잡도와 정보량을 계산하는 것은 향후 더 중요한 정보를 제공하는 단계로 각광 받을 것으로 예측된다. 가령 개인 맞춤 의료시대를 맞아, fMRI 같은 고해상도 최첨단 의료 이미징 기기의 사용이 증가할 것이다. 이러한 고해상도 이미지만으로 병변의 진단, 병환의 유무, 이상 현상의 발견 등이 1차적으로 진단되어야 할 때, 딥러닝 기반의 AI 진단을 위해서는 이미지 자체를 입력값으로 사용하는 것과 더불어 이미지 자체의 정보량이나 복잡도 역시 중요한 입력 정보가 될 수 있다. 따라서 계산의 효율을 높이고 정보 처리의 시간을 단축시키는 데 있어 주어진 패턴의 정보량, 엔트로피 지표의 계산은 중요한 위치를 차지하게 될 것이다.

의료 이미지뿐만 아니라 GIS 위성이나 천체망원경 등에서 얻은 다양한 이미지나 신호 조합으로 구성된 패턴의 복잡도와 질서도 계산은, 패턴 고유의 정보량을 대표할 수 있는 지표로서 다른 정보량과 연계되어 AI 정보 처리 효율을 높이고 신뢰도를 강화할 수 있는 중요한 중간단계 정보량이 될 것으로 전망한다. 인공지능 정보 처리를 위한 중요 입력 정보의 생성이라는 목적 외에도, 패턴의 고유 정보량이나 복잡도 계산은 패턴 설계에 근거한 다양한 공학적 과학적 시스템의 최적화에도 적극적으로 활용될 수 있을 것이다. 예를 들어 플라즈모닉 센서^{plasmonic sensor}를 위한 금속 나노구조체 패턴의 설계에도 패턴의 복잡도가 중요한 변수로 작용하여 어떠한 수준의 복잡도를 갖는 것이 최적의 센서 성능을 구현할 수 있게 할 것인지를 결정할 수 있다.

인공지능의 급속한 발전의 핵심에는 다름 아닌 주변 사물과 현상, 신호에 대한 ‘패턴 인식’ 성능의 급속한 발전이 놓여 있다. 따라서 앞으로 더욱 복잡다단해질 다양한 현상에서 파생되는 대량의 신호와 복잡한 데이터에 대한 패턴 인식 및 복잡도 지표 추출은 컴퓨터를 이용하여 더 세밀하고 더 깊은 단계에서 이루어질 것이다. 이를 통해 그간 우리가 놓치고 있던 숨어 있던 패턴이 발견될 수 있을 것이고, 그러한 패턴의 분석을 통해 새로운 지식이 발굴될 수 있을 것이다.