[12월의 퍼즐] 크리스마스 트리(Tree)

연말을 맞아 이번 달의 퍼즐은 크리스마스 컨셉으로 잡게 되었다. 크리스마스의 상징 중 하나라고 할 수 있는 트리. 수학계에서는 이 ‘트리’라는 단어에 별개의 뜻이 있다. 그래프 이론에서 Tree(나무)라고 하면 순환이 없는 연결 그래프를 의미한다. 즉 그래프가 연결되어 있음에도 불구하고, 여러 개의 이어진 변들을 따라 한 바퀴 빙 돌아서 다시 제자리로 돌아오는 일이 불가능하다는 뜻이다.

이러한 그래프에 나무라는 이름이 붙은 이유는, 점과 변의 위치를 잘 조정하면 마치 나무가 뿌리로부터 솟아 가지를 쳐 뻗어나가는 모양처럼 그릴 수 있기 때문이다. 하지만 오늘은 조금 다른 방법으로 이 트리를 바라보자고 한다. 우리가 크리스마스 트리를 상상할 때 가장 먼저 떠오르는 형태는 커다란 이등변삼각형 모양이다. 이에 착안하여 다음과 같은 특별한 트리, 크리스마스 트리를 정의하자.

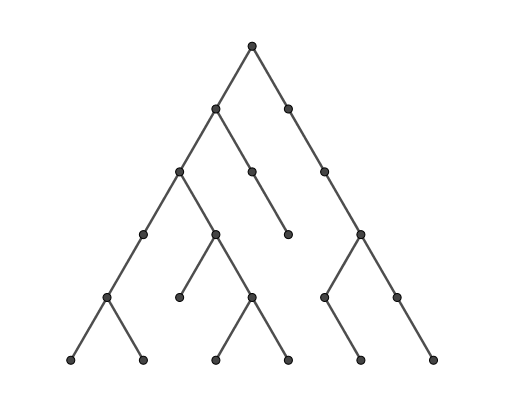
크기 \(n\)의 크리스마스 트리는 다음 세 가지 조건들을 만족하는 트리이다.

(1) 정삼각형으로 배열된 \(\frac{n(n+1)}{2}\)개의 꼭짓점을 가진다. 맨 아래층에 \(n\)개, 그 바로 위층에 \(n-1개, …,\) 맨 위층에 1개가 배치된다.

(2) 모든 변은 다음의 두 종류 중 하나이다.

즉, 꼭짓점을 자신과 인접한 (최대 6개의) 꼭짓점들과만 잇되 같은 층의 꼭짓점끼리는 잇지 않는다는 뜻이다.

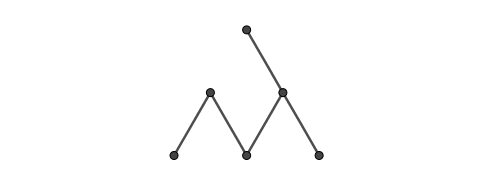
(3) 맨 위층을 제외한 모든 꼭짓점은 자신의 바로 위층에 있는 꼭짓점 중 하나와 이어져 있다. 즉, 다음과 같은 예는 크리스마스 트리가 아니다.

문제 1. 크기 \(n\)의 크리스마스 트리는 총 몇 가지가 있을까? 꼭짓점들을 모두 고정하고 연결 방법만 달리한다고 가정하자.

문제 2. 다음의 4번 조건을 추가로 만족하는 크리스마스 트리를 안정적인 크리스마스 트리라고 하자.

(4) 변 1개로만 연결된 꼭짓점들은 전부 맨 아래층에만 있다.

그렇다면 크기 \(n\)의 안정적인 크리스마스 트리는 총 몇 가지가 있을까? 1번 문제와 마찬가지로 꼭짓점들을 고정하고 연결 방법만 달리한다고 하자.

문제 3. 2번 문제와 같이 크기 \(n\)의 안정적인 크리스마스 트리의 개수를 구하려고 한다. 그러나 이번엔 서로 동형(isomorphic)인 트리는 같은 것으로 세기로 하자. 지금과 같은 경우에서는, 맨 위 꼭짓점만 고정시키고 나머지 점과 변들을 재배열(점끼리 단위 길이로만 연결되는 것을 유지한 채 같은 층의 점 순서들을 재배치)해서 다른 트리를 만들 수 있을 때 두 트리가 동형이라고 보면 된다. 

이 값을 \(n\)에 대하여 직접 나타내는 것은 매우 어렵다. 대신에 점화식을 구하도록 하자. 크기 \(n\)의 안정적인 크리스마스 트리의 (동형인 것들을 제외한) 개수를 \(a_n\)이라고 할 때, \(n \geq 3\)에 대하여 \(a_n\)의 값을 \(a_1, …, a_{n-1}\)에 대한 식으로 나타내어 보자. 답까지 이르는 과정이 완벽히 엄밀하지 않아도 좋다!