매듭은 우리 삶에서 너무나 흔히 볼 수 있다. 우리가 신고 다니는 신발의 끈, 넥타이, 그리고 배달 음식을 시켰을 때 음식을 담고 있는 비닐 봉지의 매듭, 이제는 보기 힘들지만 아직 종종 사람들이 사용하는 이어폰의 줄까지. 매듭 이론은 이러한 매듭(또는 고리)들을 연구하는 수학의 한 분야이다.
수학에서 일반적으로 매듭이라 하면 우리가 생각하는 끈을 묶어 놓은 대상 보다는 묶어놓은 끈의 양 끝을 붙여 놓은 것을 다룬다. 두개의 매듭이 있을 때, 매듭을 자르지 말고 하나의 매듭에서 다른 매듭 모양으로 바꿀 수 있으면 두 매듭은 같은 매듭이다. 예를 들어 동그란 고무줄을 이용하여 무언가를 묶었을 때, 일상생활에서는 이 고무줄이 “묶여 있다”라고 말하기도 하지만 수학에서는 이 고무줄을 끊지 않고 사용하였기 때문에 사실 같은 매듭이라고 말한다. 즉, 우리 눈으로 봤을 때 얼핏 달라 보이는 모습을 가지고 있는 매듭이라도, 그 본질은 같은 매듭일 수 있다는 것이다.
그렇다면 수학에서는 이런 매듭을 어떻게 연구할까? 끈을 이리저리 묶어보면서 연구할 수도 있겠지만, 수학자들은 이런 매듭들을 그림을 그려서 표현하고, 기본적으로 이 그림을 이용하여 연구를 하게 된다. 이런 매듭의 그림을 매듭 다이어그램이라고 부른다.
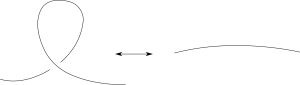
그림 1의 매듭 다이어그램을 이해하는 방법은 다음과 같다. 위의 매듭 다이어그램에서 그림 2와 같은 부분은 사실 매듭이 서로 위에서 봤을 때 겹쳐 있는 부분을 표현한 것이고, 이 중 위에 있는 부분 때문에 보이지 않는 아래 부분을 끊어서 표현을 한 것이다. 이렇게 매듭이 겹쳐보여서 다이어그램에서 끊어 그리는 곳을 우리는 매듭 다이어그램의 교차점(crossing)이라고 부른다.
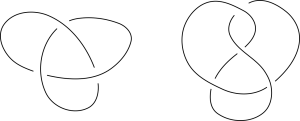

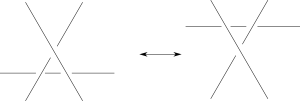
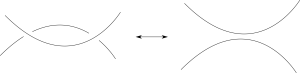
그런데 문제가 하나 있다. 앞에서 이야기한 것처럼, 비록 같은 매듭이지만 서로 다른 모습으로 그릴 수가 있다는 것이다. 쉬운 경우는 눈으로 보고 머리속으로 상상하거나, 끈을 직접 매듭 다이어그램 모양으로 묶어서 움직여 볼 수도 있겠지만, 그렇다면 굳이 그림을 그려서 연구하는 의미가 없어진다. 조금 더 체계적으로 서로 다른 그림을 비교할 수 있는 좋은 방법이 필요한 것이다. 독일의 수학자 라이데마이스터(Kurt Reidemeister)는 같은 매듭의 서로 다른 매듭 다이어그램은 그림 3의 3가지 다이어그램을 바꾸는 규칙을 통하여 서로 연결되어있다는 것을 수학적으로 증명하였다.[10] 그리고 이 3가지 규칙은 라이데마이스터의 이름을 따 라이데 마이스터 변형(Reidemeister move)라고 불리운다.
이 라이데마이스터 변형을 사용하면 그림 1의 서로 다른 매듭 다이어그램이 사실 서로 같은 매듭을 표현하는 것임을 알 수 있다.
그러면 이제 이런 방법들을 통해서 어떤 매듭을 연구할 수 있는지를 알아보도록 하자. 매듭의 종류는 무한하기 때문에 우리가 모든 것을 알 수는 없지만, 여러가지 독특한 특징을 가지고 있는 매듭들을 알아보도록 하겠다.
먼저 묶여 있지 않은 원도 수학자들은 “자명한 매듭(Trivial knot)”이라고 부르며 매듭에 포함시킨다. 이것이 가장 단순한 매듭일 것이다. 그렇다면, 누군가 풀려 있지 않은, 즉 자명하지 않은 매듭은 무엇이 있는지 물어볼 수 있을 것이다. 만약 우리가 이런 자명하지 않은 매듭의 다이어그램을 하나 예시로 그린다고 했을 때는 어떤 전략을 취하는 것이 좋을까?
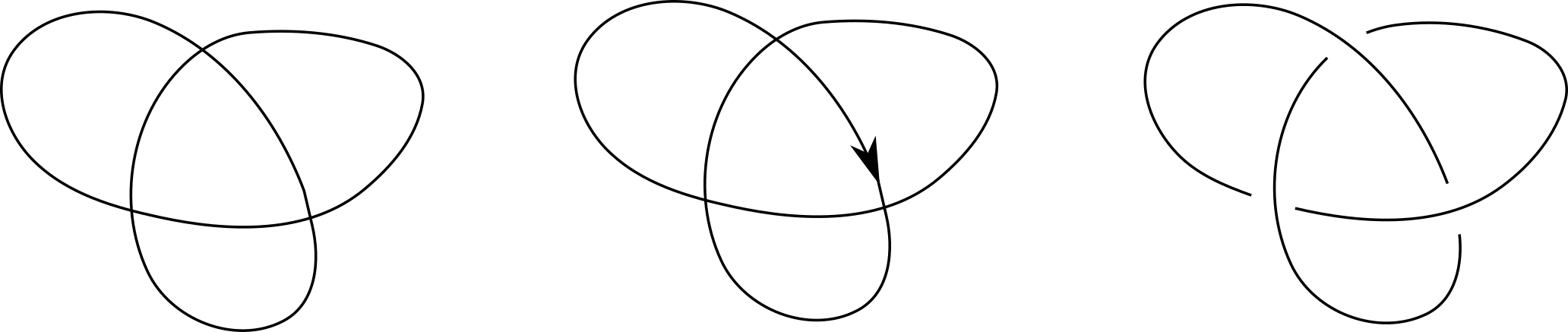
먼저 종이 위에 그림 4의 가장 왼쪽 그림과 같이 곡선을 그려보자. 그 다음, 곡선이 겹치는 곳을 이제 매듭 다이어그램의 교차점처럼 바꾸어주면 매듭 다이어그램 하나를 곡선에서부터 얻어낼 수 있을 것이다. 그런데 우리의 목적은 이 매듭 다이어그램이 최대한 자명해 보이지 않도록 하는 것이다. 이 때, 가장 자연스럽게 생각할 수 있는 방법은 바로 곡선을 따라가면서 만나는 교차점에서 매듭이 아래-위-아래-위를 번갈아 통과하도록 해주는 것이다. 이렇게 그려지는 매듭 다이어그램을 교대 매듭 다이어그램(Alternating knot diagram)이라고 부르고, 이렇게 그려진 매듭을 교대 매듭(Alternating knot)이라고 부른다. 교대 매듭 다이어그램에 작은 조건 하나를 더하면 그 교대 매듭 다이어그램이 표현하는 매듭이 자명하지 않다는 것이 알려져 있다.
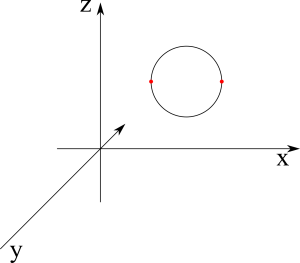
다른 방법도 하나 더 알아보도록 하자. 이를 설명하기 위해서 다음과 같은 좌표 공간을 하나 생각해보도록 하자.
여기서 x축과 z축을 포함하는 평면을 생각하고 이 평면을 z축을 따라 반으로 나누어 x 값이 0보다 큰 부분에 몇개의 점들을 그림 5와 같이 한 원 위에 있게 찍어보자.
다음, 이 점들과 그 점들을 포함하는 원을 z축을 중심으로 한바퀴 회전시키면서 동시에 점들을 원을 따라 회전시켜서 한바퀴 돌아오도록 하자. 이 때 원을 360도 회전시키지 않고 적당히 회전시켜 z축을 따라 한바퀴 돌았을때 원래 위치가 아닌 다른 점 위에 다다르게 하여 이 자취가 하나의 폐곡선이 되게 만들면 공간상에 하나의 매듭이 완성되게 된다. 이를 원환 매듭(torus knot)이라고 부른다.
앞에서 언급한 두 매듭은 가장 쉬운 매듭의 종류이고, 또한 매듭 이론의 연구에서 가장 많이 연구된 매듭들이다. 앞의 두 종류의 매듭 말고도 무수히 많은 종류의 매듭들이 있다.
하지만 여기서 수학자들은 한가지 질문을 하게 된다. 우리가 매듭을 생각할 때는 항상 3차원 공간에서만 생각하고 있다. 그러면, 과연 공간의 차원을 바꿔보면, 그 때도 매듭을 생각할 수 있을까?

3차원보다 낮은 차원으로 한번 가보도록 하자. 2차원 평면위에서 우리가 폐곡선을 생각해 보자. 이 때 주의해야 할 것은 우리가 3차원에 있는 곡선을 종이위에 표현하기 위해 곡선이 자기자신을 통과하듯이 그렸을 뿐, 3차원에서 매듭은 자기자신을 통과하지 않고 있다. 이와 마찬가지로 2차원 평면 위의 매듭을 생각할 때는 자기 자신을 통과하지 않는, 즉 단순 폐곡선(simple closed curve)를 생각해야한다. 그렇다면, 과연 2차원의 매듭은 몇 가지가 있을까? 아쉽게도 이는 조르당 곡선정리(Jordan curve theorem)에 의해 단 한가지만 있다는 사실이 알려져있다. [7] 이보다 차원이 낮아지면 곡선을 겹침없이 그리는 것이 아예 불가능하기에 더 생각할 필요가 없다.
그렇다면, 차원을 높인다면 어떻게 될까? 우리 눈에 보이지 않지만 4차원 공간에서의 매듭은 존재할까? 먼저 4차원을 어떻게 상상해야할까? 가장 보편적인 방법은 3차원 공간에 시간이라는 축을 하나 더해 4차원 공간을 생각하는 것이다. 그러면 4차원 공간에서는 어떤 매듭이 존재할 수 있을까?
4차원에서의 매듭에 대한 이야기를 하기 전에 하나 짚고 넘어가야 하는 것이 있다. 만약, 3차원 공간에서 매듭이 유령처럼 자기 자신을 통과할 수 있다면 어떻게 될까? 그러면 움직임에 아무 제약이 없기 때문에 어떤 매듭이든지 풀어 버릴 수 있을 것이다.
다시 4차원 공간으로 넘어가보자. 4차원 공간안의 매듭이 만약 특정 시간속의 3차원 공간안에 온전히 들어가 있다고 생각해보자. 그러면 다음과 같은 움직임을 통해 마치 3차원 공간에서 매듭이 자기 자신을 통과하는 것과 같은 효과를 낼 수 있다.
먼저 내가 통과 시키고 싶은 매듭의 부분을 잡고 그림 7처럼 “공간”에서의 위치는 그대로 두고 “다른 시간”으로 보내보자. 그 다음, 다른 시간에서 매듭을 움직여서 공간에서의 위치가 매듭이 자기자신을 통과하고 난 위치로 옮겨보자. 이 것이 가능한 이유는 매듭이 움직일때 통과해야하는 부분이 다른 시간속에 있기 때문이다. 그 다음, 우리가 다른 시간으로 옮겨 놓았던 부분을 원래 시간으로 움직이면 마치 매듭이 자기 자신을 통과한 것처럼 보이게 된다. 이와 비슷한 논리를 사용하면 4차원 공간에서는 자명하지 않은 매듭이 존재할 수 없다는 것을 알 수 있다.
그렇다면 4차원에서는 흥미로운 매듭이론을 할 수 없는 것일까? 여기서 수학자들은 공간이 아닌 끈 자체에 주목을 하게 된다. 4차원 공간에서 매듭이 풀렸던 이유는 우리의 매듭이 1차원이라 움직일 때 너무나 많은 여분의 차원(시간)이 있기 때문이었다. 그렇다면, 만약 우리가 1차원 매듭이 아니라, 2차원의 곡면을 4차원안에 집어 넣는다면 어떻게 될까 라는 의문을 가지게 된다.
하지만 4차원 공간조차도 상상하기 어려운데 어떻게 그 안에 들어가있는 2차원 곡면까지 상상 할 수 있을까? 수학자들은 4차원을 (3차원+시간)으로 생각한 것처럼 2차원도 (1차원+시간)으로 생각하여 이 문제를 해결하였다. 앞에서 이야기한 원환매듭을 다시 생각해보자.

원환 매듭을 생각할 때, 우리는 3차원 공간의 어떤 평면(2차원) 위에 점(0차원)들을 생각한 다음 회전시킨 점의 자취를 생각했다. 4차원 공간을 생각하기 위해선 하나씩 차원을 높여 4차원 공간안의 3차원 공간을 생각한 다음, 그 안에 1차원 곡선을 생각하여 회전시키면 그 자취가 2차원 곡면이 될 것이다. 여기서 중요한 점은 3차원 공간 안에 1차원 곡선을 생각하기 때문에 만약 이 1차원 곡선이 매듭지어져있다면, 그 자취인 4차원 공간안의 2차원 곡면도 매듭이 지어져 있을 수 있는 것이다. [1, 2]
이렇게 만들어진 3차원 공간의 매듭과 4차원 공간의 매듭지어진 곡면들은 위상수학, 특히 저차원 위상수학이라고 불리우는 분야에서 널리 연구되고 있다. 단순히 매듭을 분류하고 그 특징들을 연구하는 것을 넘어서 이런 매듭들은 매듭들을 포함하고 있는 다양체라고 불리우는 공간의 위상수학/기하학 연구에도 널리 활용되고 있다. [5, 8, 12] 더 나아가 양자 컴퓨터 [4], 단백질 접힙 현상 [9, 11] 등 다른 과학분야와도 연관이 있으며 최근에는 데이터 분석 및 기계학습 등의 방법을 이용한 매듭 이론의 연구도 많이 하고 있다. [3, 6]
매듭 이론은 일반적인 교과 과정상 다루기 힘든 부분이 많아 대부분의 사람들에게 생소한 분야일 것이다. 하지만 분명 흥미로운 미해결 문제들이 많이 있고 활발히 연구되고 있는 수학분야이기에 이 글을 통해 조금이라도 더 많은 사람들이 매듭이론에 관심을 가지길 바란다.
참고 문헌
[1] Emil Artin. Zur Isotopie zweidimensionaler Fl¨achen im R4. Abh. Math. Sem. Univ. Hamburg, 4(1):174–177, 1925.
[2] Jeffrey Boyle. The turned torus knot in s 4. Journal of Knot Theory and Its Ramifications, 2(03):239–249, 1993.
[3] Alex Davies, Petar Veliˇckovi´c, Lars Buesing, Sam Blackwell, Daniel Zheng, Nenad Tomaˇsev, Richard Tanburn, Peter Battaglia, Charles Blundell, Andr´as Juh´asz, et al. Advancing mathematics by guiding human intuition with ai. Nature, 600(7887):70–74, 2021.
[4] Michael Freedman, Alexei Kitaev, Michael Larsen, and Zhenghan Wang. Topological quantum computation. Bulletin of the American Mathematical Society, 40(1):31–38, 2003.
[5] Herman Gluck. The embedding of two-spheres in the four-sphere. Trans. Amer. Math. Soc., 104:308–333, 1962
[6] Mark C Hughes. A neural network approach to predicting and computing knot invariants. Journal of Knot Theory and Its Ramifications, 29(03):2050005, 2020.
[7] Camille Jor dan. Cours d’analyse de l’Ecole polytechnique: t. Equations diff´erentielles ordinaires. Equations lin´eaires. Equations aux d´eriv´ees partielles. Calcul des variations, volume 3. Gauthier-Villars et fils, 1887.
[8] W. B. R. Lickorish. A representation of orientable combinatorial 3-manifolds. Ann. of Math. (2), 76:531–540, 1962.
[9] Marc L Mansfield. Are there knots in proteins? Nature structural biology, 1(4):213–214, 1994.
[10] Kurt Reidemeister. Elementare begr¨undung der knotentheorie. In Abhandlungen aus dem Mathematis-chen Seminar der Universit¨at Hamburg, volume 5, pages 24–32. Springer, 1927.
[11] William R Taylor. A deeply knotted protein structure and how it might fold. Nature, 406(6798):916–919, 2000.
[12] Andrew H. Wallace. Modifications and cobounding manifolds. Canadian J. Math., 12:503–528, 1960.