[7월의 퍼즐] 도미노와 4색 문제

7월의 퍼즐을 소개하기에 앞서 4색 문제에 대해 이야기해 보자.

평면을 몇 개의 영역으로 나눈 지도를 생각해 보자. 여러분이 할 일은 이 지도를 색칠하는 것이다. 색칠할 때는 몇 가지 규칙이 있다. 각 영역은 한 가지 색으로 칠해야 하며, 경계선을 따라 인접한 두 영역은 서로 다른 색으로 칠해서 구분 짓기 쉽게 해야 한다. (꼭짓점끼리만 닿는 두 영역은 같은 색이어도 된다.) 모든 영역을 각기 다른 색으로 칠해도 되겠지만, 이왕이면 적은 종류의 색으로 칠하는 것이 경제적일 것이다.

예를 들어, 아래와 같이 대한민국의 행정 구역을 나타낸 지도를 네 가지 색만으로 칠할 수 있다. 예시 외에도 직접 다양한 지도를 색칠해 보자. 아무리 복잡하게 생긴 지도라도 네 가지 색이면 충분할 것이다. 그렇다면 정말로, 모든 평면 지도를 네 가지 색으로 칠하는 것이 가능할까?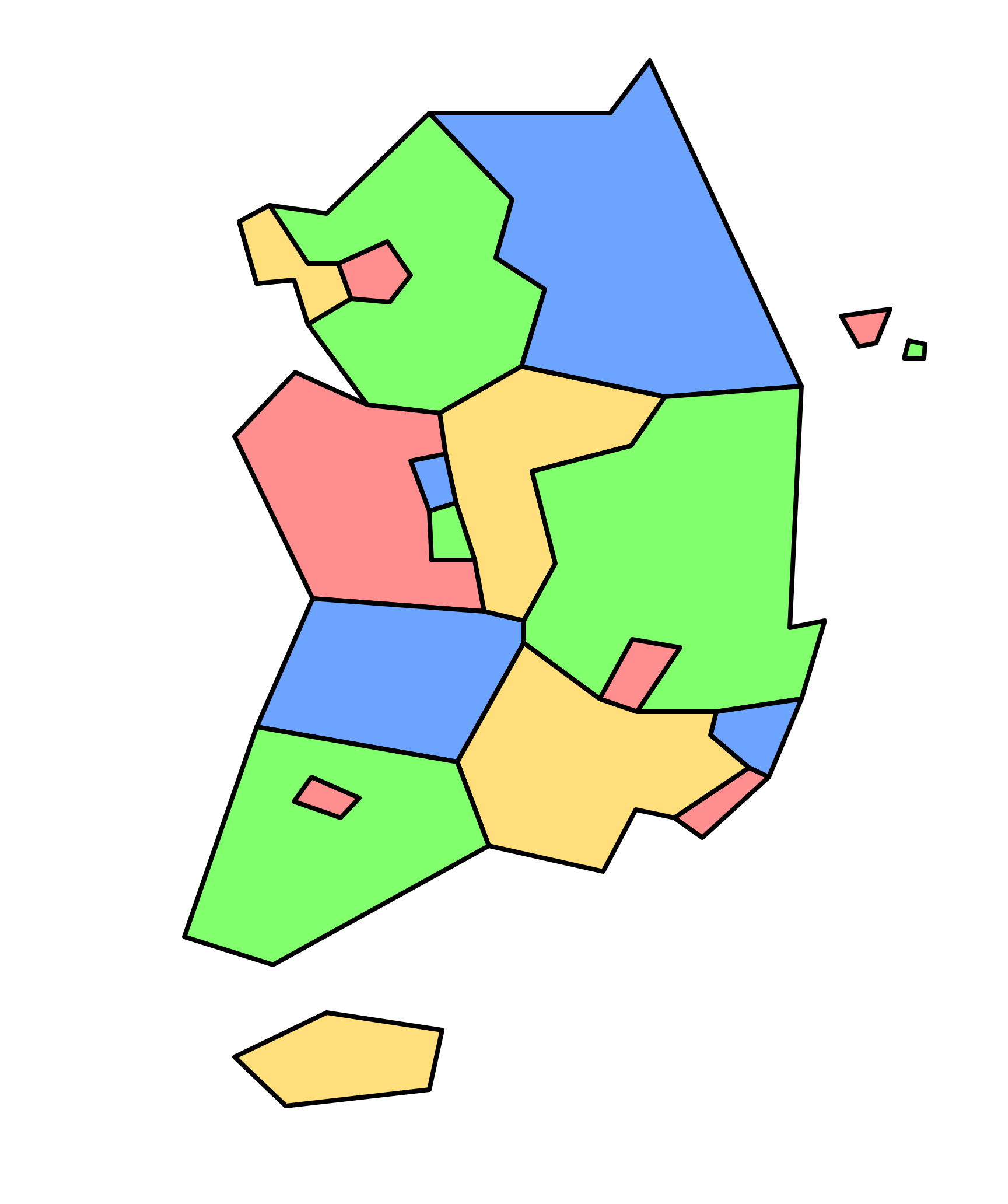
이 문제는 4색 문제라고 불리며, 1852년 프란시스 거스리^{Francis Guthrie}가 영국의 지도를 색칠하다가 떠올린 문제이다. 4색 문제는 백여 년 동안 난제였다가 1976년 케니스 아펠^{Kenneth Appel}과 볼프강 하켄^{Wolfgang Haken}에 의해 참임이 증명되었다.

하지만 그 증명은 컴퓨터를 이용해서 천 가지가 넘는 경우의 수를 직접 확인하는 방식이었기 때문에, 인간이 이해하기에는 어려운 증명이었다. 더 아름다운 증명을 찾고자 하는 많은 수학자의 노력에도 불구하고, 지금까지 컴퓨터를 사용하지 않는 증명이 발견되지 않았다. 여러분은 아름다운 증명을 찾을 수 있을까?

***

물론 이번 퍼즐에서 여러분에게 4색 정리의 증명을 시키는 것은 너무 가혹할 것이다. 대신 조금 특수한 지도를 생각해 보자. 모든 영역이 2×1 크기의 직사각형, 즉 도미노 모양이라고 가정한다면 어떨까? 각 도미노는 격자에 맞게 배치되어 있다고 하자. 또한, 도미노로 둘러싸인 빈 곳이 있을 수도 있다. 예를 들면 아래와 같은 지도를 생각할 수 있겠다.


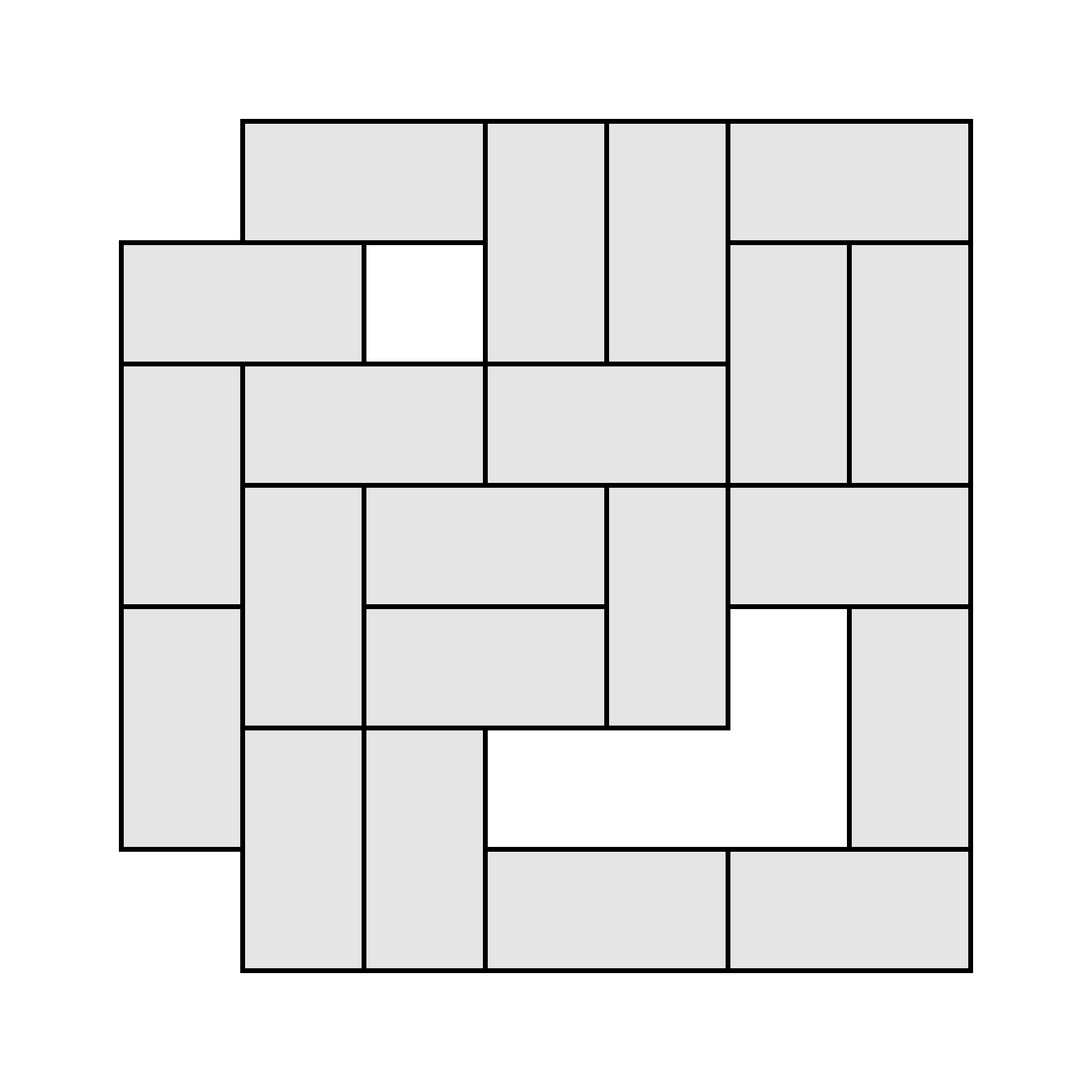
어떤 도미노 배치가 주어지든, 모든 도미노를 네 가지 색으로 색칠하는 방법을 고안해 보자. 4색 정리에 따르면 이것이 항상 가능하겠지만, 4색 정리가 임의의 도미노 배치를 색칠하는 방법을 말해 주지는 않는다. 여러분은 모든 도미노를 네 가지 색으로 색칠하는 아름다운 방법을 찾을 수 있겠는가?