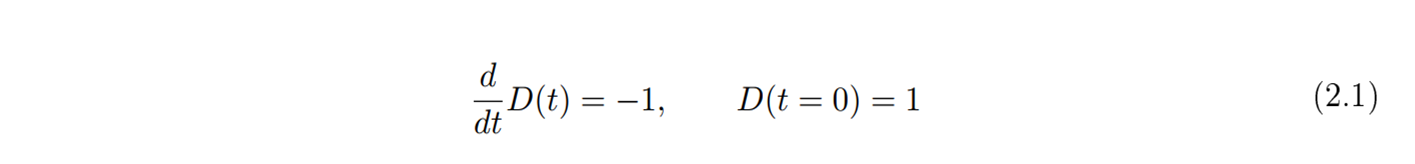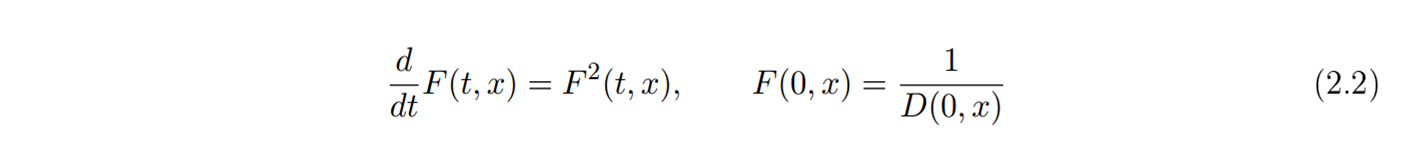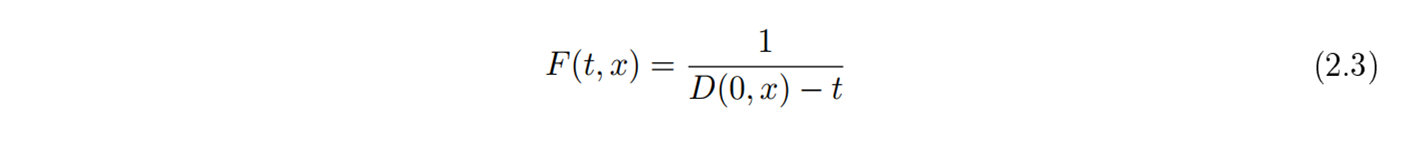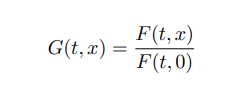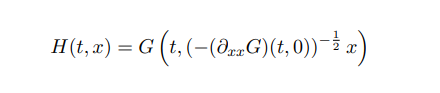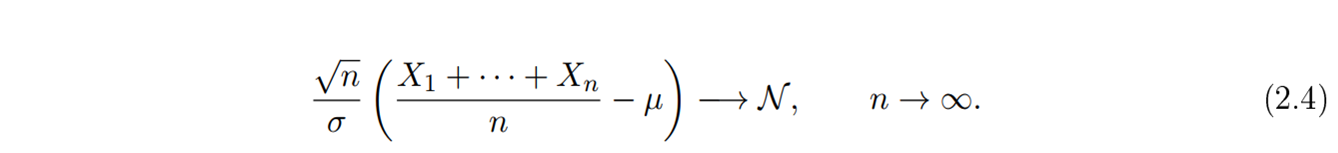미분방정식의 특이점 형성에 관하여

클레이 수학연구소가 제시한 7개의 난제 중에서도 비압축성 나비어-스톡스 방정식의 정칙성과 특이점 형성에 대한 문제는 상대적으로 널리 알려져 있는 것 같습니다. 나비어-스톡스 방정식은 대기의 흐름을 기술하는 근본적인 방정식이며, 이 방정식의 특이점 형성 여부는 순수 수학적으로도 매우 도전적일 뿐 아니라 기상 현상의 예측 가능성과도 관련되어 중요한 문제입니다. 최근에 이르러 컴퓨터 연산 능력의 비약적인 상승과 함께 편미분 방정식 이론의 발전으로 나비어-스톡스 방정식의 특이점 형성의 증명에 이르는 로드맵이 여러 연구자에 의하여 제시되고 있고, 이러한 내용은 퀀타 매거진에 의해서도 몇 차례 소개된 바 있습니다[1,2] . 이 글에서는 미분방정식에서 특이점의 의미와 함께, 어떻게 컴퓨터를 이용한 계산이 특이점 형성의 증명, 특히 이 나비어-스톡스 방정식에 관한 7대 난제의 해결에 기여할 수 있는 지에 관하여 이야기해보려고 합니다.

     특이점을 설명하기에 앞서, 미분방정식이란 어떤 함수(종속변수)의 다양한 미분값들이 만족하는 방정식을 의미합니다. 보다 구체적으로, 나비어-스톡스 방정식을 비롯한 물이나 대기(통틀어 유체라고 함)의 흐름을 기술하는 방정식은 그 유체의 속도, 압력, 밀도와 같은 함수들의 시간 미분과 공간 미분이 만족하는 관계식입니다.

     특이점이란 개념은 미분방정식 분야로 한정하여도 다양한 의미를 갖기 때문에 모든 상황을 포괄하는 정의를 내리기는 어려운 일이지만, 논의를 구체화하기 위하여 하나의 시도를 해 보자면 대략적으로 “시간에 따라서 어떤 미분방정식을 만족하며 변화하는 물리량이 있을 때, 어떤 특정한 시간에 갑자기 모종의 이유로 더 이상 고전적인 방법으로 그 물리량이 어떻게 변해 나갈지 결정할 수 없는 상황”을 특이점이라고 이야기할 수 있을 것 같습니다. 어떤 특정한 물리 현상을 설명하는 미분방정식에서 특이점이 형성된다고 했을 때, 그 특이점을 우리가 어떻게 해석해야 하는지는 상당히 미묘한 문제입니다. 앞서 제시한 특이점의 정의에 함축되어 있는 것은, 이 개념이 수학적으로는 특정 {방정식에 종속}된다는 것입니다. 즉, 특이점이 발생하는 이유는 단순히 그 미분방정식이 현실을 지나치게 단순화하여 주요한 효과를 담지 못했을 가능성과 함께, 미분방정식 자체는 합당하지만 수학적으로 우리가 그것을 올바르게 푸는 방법을 모르는 가능성이 함께 존재합니다. 다시 말해서 특이점의 존재는 물리 모델링 단계에서 해결해야 하는 과제일 수 있고, 방정식의 풀이에 대한 이론을 개선해야 하는 과제일 수 있습니다. 

    유체방정식의 경우로 한정하여도, 여러 가지 흥미로운 상황에서 특이점이 형성된다는 것이 잘 알려져 있고, 각각의 경우에 특이점을 올바르게 해석하는 것은 흥미로운 문제가 됩니다. 예를 들어, 해안가에서 파도가 일렁이는 모습을 보면, 파고가 점점 높아지다가 어느 시점에 부서져 내리는 상황을 관찰할 수 있습니다. 그런데, 이러한 파도의 움직임을 기술하는 많은 편미분 방정식에서, 파도의 경계면은 매끈한 함수로 기술된다고 가정하고 있기 때문에, “파도가 부서지기 직전의 순간”에 특이점이 형성된다고 볼 수 있습니다. 또 다른 예로는 항성의 중력 붕괴, 쇼크웨이브의 형성 등을 들 수 있습니다.

    다양한 특이점의 사례는 우리에게 많은 호기심을 불러일으킬 뿐 아니라, 특이점 형성의 문제는 미분방정식을 이용한 미래의 예측이라는 관점에서 특히 더 흥미롭고 중요합니다.  가장 좋은 예는 날씨의 예측이고, 나비어-스톡스 방정식이 갖는 큰 의의가 바로 이 방정식이 (극단적으로 단순한 상황에서) 대기의 흐름을 잘 기술한다고 믿어지는 데 있습니다. 고전적으로는, (1) 날씨의 흐름을 관장하는 미분방정식을 정확하게 알고 있고, (2) 현재의 대기 상태를 한없이 작은 오차범위 내로 측정할 수 있으면, 우리가 미래의 날씨를 알 수 있게 됩니다. 물론 각각이 매우 비현실적인 조건이지만, 이 조건들이 성립된다고 할지라도 사실 하나의 커다란 조건이 추가적으로 필요한데, 그것이 바로 “날씨의 흐름을 기술하는 그 미분방정식(예를 들어 나비어-스톡스 방정식)이 유한한 시간 내에 특이점을 형성하지 않는다”는 것입니다. 다시 말해서, 특이점이 어떤 시간에 형성된다면, 그 이후 날씨의 예측은 근본적으로 불가능한 문제일 수 있습니다. 결정론적인 입장(미래가 현재 상태에 의하여 결정되어야 한다는 믿음)에서는 특이점의 존재 자체가 앞선 (1)의 가정에 모순처럼 보이지만, 결정론적 논의와 무관하게 순수하게 수학적인 관점에서는 충분히 (1)과 특이점의 존재가 양립할 수 있습니다. 실제로, 기상학자였던 로렌츠는 이미 1969년 논문에서 날씨의 예측은 불안정성으로 인한 어려움을 넘어서, 특이점 형성으로 인하여 근본적으로 불가능한 일이라고 주장하고 있습니다[3].

2  자기닮은꼴의 안정적인 특이점 형성

이제 특이점 형성 과정의 자세한 설명을 위하여 극단적으로 단순화된 예시를 들어 보려고 합니다. 우리가 거리가 1만큼 떨어진 벽에 일정한 속도 1로 화살을 수직하게 쏘는 상황에서, 화살과 벽까지의 거리를 시간  에 대한 함수  라고 정의한다면, 이 함수가 만족하는 미분방정식은

이 됩니다. 이 미분방정식의 해는 t 가 0과 1사이에 있는 경우  =  가 되는데,  인 순간 화살이 벽에 충돌하면서  인 경우에는 방정식 (2.1)이 의미를 갖지 않게 됩니다.¹ 그러므로  인 순간에 방정식 (2.1)의 특이점이 형성된다고 볼 수 있는데, 이제 이 상황을 조금 일반화시켜 벽과 평행한 좌표계를 라고 나타낼 때, 각 위치 마다 궁수가 어떤 거리  로부터 속도 1의 화살을 동시에 벽으로 수직하게 쏘는 상황을 생각해볼 수 있습니다. 놀랍게도 이 간단한 일반화에서, 특이점 형성 (이 경우에는 벽과 화살의 충돌)의 자기닮음성과 안정성을 확인할 수 있습니다. 이를 쉽게 드러내는 것은 새로운 변수 인데, 여기에서 는 위치 상에서 시간 t 에 벽과 화살과의 거리를 나타냅니다. 그러면 가 만족하는 미분방정식은

이 됩니다. 이제 논의를 간단히 만들기 위하여  인 점에서 최소값 1을 갖는 적당한 함수 을 택하여 (2.2)의 해의 그래프가 어떻게 변하는지 조사해 봅시다. 해의 공식

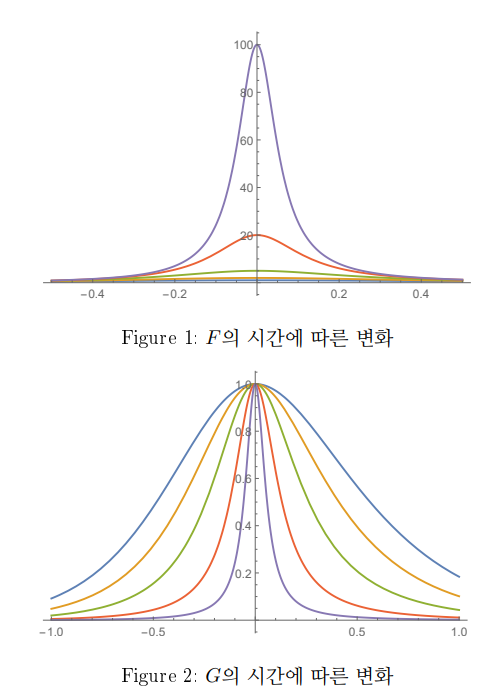
을 이용하여  0, 0.5, 0.8, 0.95, 0.99 일 때 해의 그래프를 그려보면 그림 1과 같습니다. 시간이 1이 되는 순간 점 에서 화살이 벽에 충돌하므로, 거리의 역수로 정의된 는 에서 t가 1에 다가갈수록 무한대로 발산하게 됩니다. 그런데,  에 접근하면서 발산하는 이 그래프들은 사실 특별한 보편성(universality)를 가지고 있습니다. 이를 확인하기 위하여, 우선 각 시간 t에 대해

함수의 최대값을 1로 변환시키는 조작

을 가해주고, 같은 시간들에 대해 G의 그래프를 그려보면 이제 그림 2를 얻습니다. 이 경우, 에 접근할수록 함수의 그래프는 한없이 뾰족해짐을 알 수 있습니다. 이 것을 “올바르게” 펼쳐주기 위하여, 축을 시간에 맞게 늘려서 함수의 그래프가 항상 최대값에서 2계 도함수 값을 -1로 갖도록 할 수 있습니다. 공식으로는, 단순히

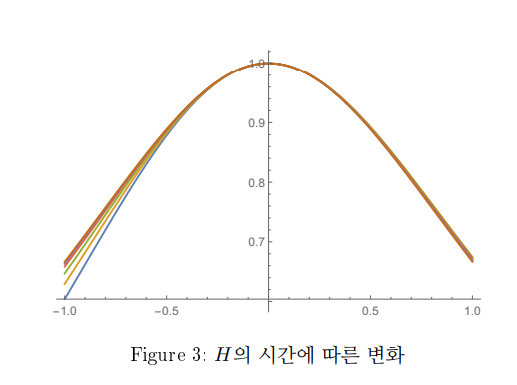
입니다. 마지막으로, 같은 시간들에 대해 의 그래프를 그려 보면 그림 3을 얻는데, 여기에서 나타나는 충격적인 사실은, 에 접근할수록 함수들의 그래프가 정확하게 라는 특별한 함수로 수렴한다는 것입니다.²

마지막 그림 3이 방정식 (2.2)의 특이점이 안정적인 자기닮음꼴이라는 것을 생생하게 보여줍니다. 여기에서, 자기닮음이라는 것은 기하학에서 도형의 닮음과 같은 개념으로, 시간이 특이점에 다가갈수록 함수의 그래프들이 서로 닮아 있다는 것을 의미합니다. 이것을 확인하게 위해서 우리는 그래프의 함수축 (로의 변형)과 축 (G에서 H로의 변형)을 시간에 따라 적절하게 변형시켜 주어야 했습니다. 앞으로 이 과정을 편의상 규격화라고 부르겠습니다. 이제, 특이점 형성이 안정적이라는 의미는, 우리가 규격화를 통해서 특이점이 형성되는 순간에 보게 되는 함수(이 경우에는  )가, 초기에 어떤 함수로 시작했는지와 무관하게 같다는 것입니다. 앞으로 이 특별한 함수를 프로파일이라고 하겠습니다. 방정식 (2.2)의 경우에는 해의 공식 (2.3)에 테일러 전개를 이용하여 특이점의 자기닮음성과 안정성을 간단하게 증명할 수 있습니다. 다만, 보다 복잡한 미분방정에 대해서는  일반해가 대부분의 경우 알려져 있지 않기 때문에, 특이점 형성이 일어난다고 할 때 우선 프로파일을 찾는 것 부터 시작해서 안정성을 증명하는 것은 어렵고 흥미로운 문제가 됩니다. 

    여기에서 자기닮음성과 안정성의  다른 예시로 확률론에서 나오는 중심 극한 정리(CLT)를 생각할 수 있습니다. 간단히 말해, CLT는 서로 독립이고 같은 분포를 갖는 확률 변수 들이 기대값 와 분산 를 가지고 있을 때, n개의 합 을 적절하게 변형해 주면 평균 0, 분산 1인 정규분포 로 수렴하게 된다는 것입니다.³:

여기에서 식 (2.4)의 좌변을 보시면 합 에 세 가지의 변형을 가해야 정규분포가 나오는 것을 알 수 있는데, (i) 으로 나누기, (ii) 를 빼기, (iii) 마지막으로 를 곱해주기 입니다. 이 세 가지 조작은 사실 위의 특이점 형성 상황에서 (i) 함수의 최대값을 1로 맞추기, (ii) 특이점이 에 형성되게 하기 (이 조작은 위 예시에서는 최대값이 에서 유지되므로 할 필요 없었음), (iii) 마지막으로 2계 미분의 값을 1로 맞추기에 해당합니다. 실제로, 편미분 방정식 이론에서 개발된 특이점의 안정성 증명과 정확하게 같은 테크닉으로 CLT를 증명하는 것이 가능합니다[4].

비압축성 나비어-스톡스 방정식이 특이점 형성을 일으킨다는 것을 증명함으로서 7대 난제를 해결하기 위해서는, 유체의 속도가 어떤 특정한 시간에 무한대로 발산한다는 것을 보여야만 합니다. 이러한 종류의 명제를 증명하는 것은 컴퓨터가 도와줄 수 없는 것처럼 보이지만, 최소한 방정식의 특이점 형성이 안정적인 경우에는 그렇지 않으며, 간단하게 그 이유를 설명해 드리려고 합니다. 

    우선 우리가 어떤 미분방정식이 갖는 특이점 형성의 프로파일을 (모종의 이유로) 알고 있는 경우를 생각할 수 있는데⁴, 그러면 이 프로파일의 안정성이란, 그에 대한 섭동⁵이 규격화를 거친 후 시간에 따라 프로파일로 다시 수렴해 간다는 뜻입니다. 그런데, 섭동의 시간에 따른 움직임은 선형화된 방정식으로 묘사할 수 있고, 선형화된 방정식은 중첩원리로 인하여 그 이해가  일반적인 비선형 방정식보다 훨씬 수월하게 됩니다. 보통은 “충분히 작은” 섭동이 프로파일로 수렴해 나간다는 것만 확인하면 되는데, 섭동의 방정식에 대한 매우 세밀한 연구를 통하여 안정성의 정량화를 할 수 있습니다. 즉, 비선형 방정식에서 프로파일로 규격화 후 수렴해 나가는 것이 보장되는 구체적인 섭동의 “크기”를 계산해낼 수 있다는 것입니다. 이 단계에서 섭동의 크기를 구체적으로 어떻게 잴 것이냐에 관하여 많은 아이디어가 필요하게 됩니다. 그리고 이 안정성의 정량화 단계에서도 컴퓨터가 크게 기여할 수 있는데, 이것은 구체적으로 어떤 숫자를 제시하는 종류의 문제이기 때문이고, 보다 근본적으로 이 정량화는   프로파일을 정확하게 알지 못하는 상황에서 핵심적인 역할을 하게 됩니다. 

    비압축성 나비어-스톡스 방정식을 비롯한 여러 편미분 방정식에서 우리는 특이점의 프로파일에 대한 어떠한 정보도 갖고 있지 않으며,⁶바로 이 부분이 이 난제에 컴퓨터가 가장 크게 기여하고 있는 부분인데, 컴퓨터의 탐색을 통하여 근사적인 프로파일을 찾아낼 수 있다는 것입니다.⁷여기에서 중요한 포인트는 프로파일을 근사적으로만 찾으면 된다는 것인데, Hou의 그룹이 실행중인 전략은 다음과 같습니다.⁸

적당한 초기 조건으로부터 슈퍼컴퓨터를 이용하여 비압축성 나비어-스톡스 방정식을 수치적으로 풀어 나가고, 공간상에서 특이점이 형성되는 것 처럼 보이는 점 근처에서 적절한 규격화를 시시각각 해 나가면서 만약 함수가 어딘가로 수렴하는 것 처럼 보이면, 컴퓨터에게 적당한 근사함수(예를 들면 고차 다항식)을 달라고 요구합니다. 여기에서 중요한 포인트는, 우리에게 어떤 구체적인 함수가 주어지면, 그 함수가 나비어-스톡스 방정식을 얼만큼의 오차를 가지고 푸는지 매우 쉽게 계산할 수 있다는 것입니다.⁹  이제, 이 근사함수 근처에서 나비어-스톡스 방정식을 선형화를 연구할 수 있는데, 근사함수가 구체적으로 주어져 있으므로, 선형화된 방정식도 매우 구체적이고, 이 방정식의 안정성을 정량화할 수 있습니다. (물론, 이 방정식이 안정적이지 않다면, 이 전략을 수정하여야만 합니다.) 많이 과장해서 말하면, 이제 이 7대 난제가 단순히 두 개의 숫자(이 근사함수가 가지는 오차와 정량화된 안정성의 척도)의 크기를 비교하는 문제로 환원됩니다. 여기서 명백하게 드러나는 것이, 안정성의 정량화가 프로파일을 근사적으로만 찾아도 된다는 것을 의미하고, 즉 컴퓨터가 크게 기여할 수 있는 길을 열어주었다는 것입니다. 이 훌륭한 전략에서 첫 번째 커다란 난관은 바로 비압축성 나비어-스톡스 방정식을 수치적으로 푸는 것이 극도로 많은 시간과 자원을 필요로 한다는 것인데, 이에 관련하여 최근에 주목을 받고 있는 논문 [7]에서는, 시간에 따른 방정식의 수치 풀이를 하지 않고, 뉴럴 네트워크를 이용하여 단순히 근사적인 프로파일만 잡아내는 전략을 도입하여 효율적으로 이 단계를 해결할 수 있다고 이야기하고 있습니다. 

    이 글을 마무리하며 간단하게 나비어-스톡스 방정식 문제의 풀이가 갖는 의의에 대해 이야기하려고 합니다. 만약에 특이점 형성이 특정한 프로파일을 가지고 자기닮음 형태로 나타난다는 것이 증명된다면, 그로부터 특이점의 관측 가능성, 특이점 이후의 동역학과 예측가능성의 문제, 현상론적으로 정립된 난류 이론과의 관계 등 물리학적으로도 매우 중요한 여러 문제들의 연구를 본격적으로 시작할 수 있게 됩니다. 다시 말해서, 비압축성 나비어-스톡스 방정식의 특이점 형성 문제는 이 분야의 어떤 종착지라기보다는, 반대로 비로소 근본적으로 중요한 문제들에 접근할 수 있는 입구라고 보는 것이 맞습니다. 마지막으로, 우리가 나비어-스톡스 문제의 해결에 이르지 못한다고 할지라도, 이 과정에서 탄생한 새로운 아이디어와 기술이 이미 우리가 미분방정식을 이해하는 새로운 길을 활짝 열어놓았다는 사실은 명백합니다.