4월의 퍼즐에 참여해주신 모든 분들께 감사드리며,
참여해주신 분들 중 정답과 함께 좋은 풀이를 보내주신
김형진 님에게 문화상품권을 전달하겠습니다.
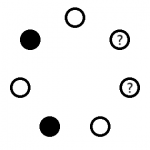
힌트에서 말한 것과 같이 고장난 전구가 원형으로 배치되어 있다고 생각하고, 고장난 두 전구가 떨어져 있는 경우와 붙어 있는 경우로 나누자.
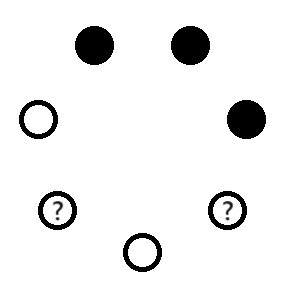
고장난 두 전구가 떨어져 있다면 힌트와 동일한 방법으로 구분할 수 있다. 즉, 각 고장난 전구의 왼쪽 전구만 켜면 된다. 그림으로 표현하면 다음과 같다. 흰색 원은 켜진 전구를, 검은색 원은 꺼진 전구를, 물음표는 고장난 전구를 말한다.
이렇게 하면 충명은 항상 (켜짐/켜짐) 또는 (켜짐/꺼짐) 전구쌍을 정확히 2개 찾을 수 있으며, 각 전구쌍에서 오른쪽의 전구가 고장난 전구라고 확신할 수 있다.
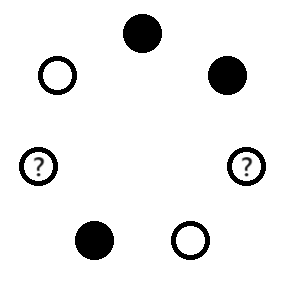
이제 고장난 전구가 붙어 있는 경우를 생각해 보자. 위의 경우와 헷갈리면 안 되므로 나머지 5개 전구 중 다음의 3개는 확실히 켜 놓도록 하자.
이렇게 하면 전구쌍 2개로는 켜진 전구들을 모두 설명할 수 없으므로, 고장난 두 전구가 떨어져 있는 경우와 헷갈릴 일은 없다. 이제 남은 전구 2개를 켤지 끌지 결정해야 한다.
만약 그림을 회전해서 이 경우의 다른 가짓수와 겹칠 수 있다면 충명이 고장난 전구 두 개가 무엇인지 확신할 수 없게 되는 문제가 생긴다. 가령 남은 두 전구를 모두 끈다고 해 보자. 그러면 충명이 다음과 같은 전구 배치를 보았을 때 고장난 전구 두 개가 무엇인지 확신할 수 없게 된다.
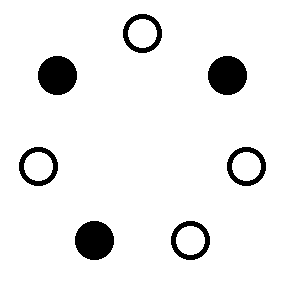
남은 두 전구를 모두 켠다고 해도 마찬가지의 문제가 발생한다. 예를 들어 충명이 모든 전구가 켜져 있는 상황을 마주한다면 고장난 전구 두 개가 무엇인지 확신할 수 없게 된다.
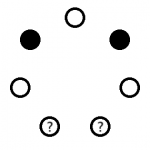
이를 피하기 위해서는 남은 두 전구 중 하나는 켜고 하나는 끄면 된다. 가령 다음과 같은 패턴으로 전구를 켜겠다고 합의해 두면 그림을 회전해서 다른 가짓수와 겹칠 일이 없다.
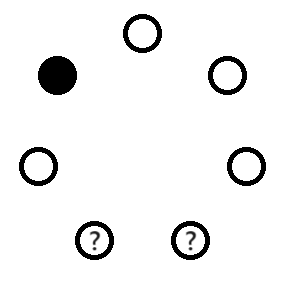고장난 전구가 어떤 상태가 되더라도 이 원순열에서 (켜짐/켜짐/켜짐/꺼짐/켜짐) 패턴은 단 하나만 찾을 수 있고, 따라서 패턴에 포함되지 않는 두 전구를 고장난 전구라고 확신할 수 있다.
물론, 고장난 전구가 붙어 있는 경우에서 다른 하나의 패턴을 선택해도 아무런 문제는 없다. 그러면 (켜짐/꺼짐/켜짐/켜짐/켜짐) 패턴을 찾으면 될 것이다.
여담으로 이 문제는 그래프 문제로 환원할 수 있다. 이 문제는 2^7 = 128개의 꼭짓점을 갖는 7차원 하이퍼큐브의 꼭짓점들을 4개씩 묶어서, 모든 변과 수직이거나 평행하고, 서로 수직이고, 서로 꼭짓점을 공유하지 않는 7C2 = 21개의 면을 찾는 문제와 동치다. 간단히 설명해 보자.
7개의 전구가 각각의 축을 나타내고, 각 전구가 켜진/꺼진 상태일 수 있으므로 각 축마다 2가지 경우의 수가 가능하다. 그러면 128가지 모든 경우의 수가 7차원 하이퍼큐브로 도식화된다는 것은 쉽게 받아들일 수 있을 것이다. 충명은 이 중에서 하나의 꼭짓점을 관측하게 될 것이고, 미리 합의한 바에 따라 그 꼭짓점이 어느 면에 속하는지 알 것이므로, 그 평면과 평행인 두 축을 나타내는 두 전구가 고장난 전구라고 말하면 된다. 당신은 고장난 두 전구가 나타내는 두 축을 알고 있으니, 그 두 축과 평행한 2^5 = 32개의 평면 중에서 미리 합의한 리스트에 있는 면을 골라 그에 맞게 전구를 조작하면, 고장난 전구가 어떤 상태가 되더라도 당신이 고른 면 안의 꼭짓점 중 하나가 충명에게 전달되고 충명은 미리 합의한 바에 따라 그 면을 복구해낼 것이므로 문제가 없다.
128개의 꼭짓점 중 겨우 84개만 풀이에 사용하므로 척 봐도 다양한 답이 나올 수 있어 보일 텐데, 실제로도 풀이에서 소개한 것 외에 굉장히 다양한 해답이 존재한다. 풀이에서 소개한 답은 출제자가 찾은 가장 간단한 방법이다.
