[11월의 퍼즐 해설] 귀엽고~ 깜찍하게~ 써리~ 원!

두 팀을 A, B로 표기하자. 동규의 팀이 둘 중 어디인지는 아직 정해지지 않았다. 가능한 플레이어 배치를 모두 고려하면 다음과 같다. 회전해서 같은 경우나, 두 팀의 이름을 바꿔서 같은 경우는 제외했다.

1. AAABBB
   2. ABABAB
   3. AABBAB

설명의 편의를 위해 주어진 게임을 1부터 1000까지의 수를 부르는 게임 대신 1000개의 돌 더미에서 돌을 가져가는 게임으로 생각하자. 돌아가면서 돌을 3개 이하씩 가져가다가, 마지막 돌을 가져가는 사람이 지는 것이다.

이제 각 배치에서, 각 플레이어가 자기 차례에 n개의 돌을 받은 경우 승리할 수 있는지를 표로 나타낼 것이다. n = 1000인 경우를 확인하면 그 플레이어가 첫 턴을 가져갔을 때의 승패 여부를 알 수 있다. 일단 누구든 자기 차례에 1개의 돌이 남았다면 패배한다. 내 차례에 남은 돌이 n개일 때, k개의 돌을 가져가면 다음 플레이어에게 n-k개의 돌을 넘겨주게 된다. 경우에 따라 아래와 같이 승패가 결정된다.

• 다음 플레이어가 같은 팀인 경우
  (a) 다음 플레이어가 돌을 n-k개 받았을 때 승리하는 경우가 있다면, 돌을 k개 가져가서 우리 팀이 승리할 수 있다.
  (b) 그렇지 않다면 돌을 몇 개 가져가든 우리 팀이 패배한다.
•  다음 플레이어가 다른 팀인 경우
  (c) 다음 플레이어가 돌을 n-k개 받았을 때 패배하는 경우가 있다면, 돌을 k개 가져가서 우리 팀이 승리할 수 있다.
  (d) 그렇지 않다면 돌을 몇 개 가져가든 우리 팀이 패배한다.

위 규칙에 따라 표를 채워 보자. 승리를 O, 패배를 X로 표기하면, 1번 배치의 경우 다음과 같이 표가 만들어진다.

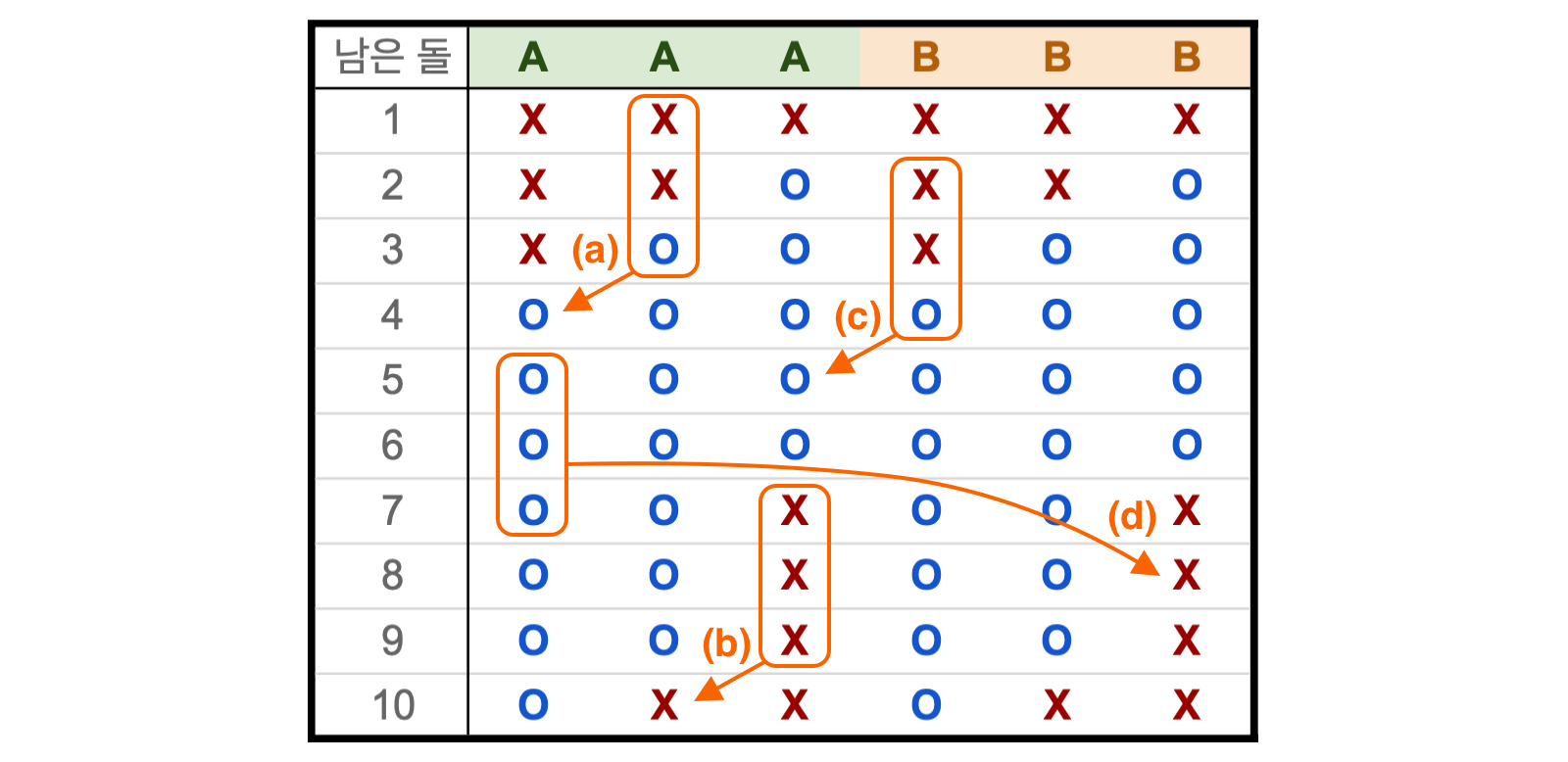
사람 손으로 표를 1000 줄이나 채우는 건 힘드니 패턴을 찾아야 한다. 각 행의 승패 정보는 앞 세 행의 승패 정보에 의해 결정되므로, 어떤 a행과 b행의 앞 세 행이 완전히 일치한다면 a행과 b행의 승패 정보도 일치할 것이다. 그러면 a+1행과 b+1행도, 그리고 그 뒤의 행들도 연달아 일치하여 표에 주기성이 생긴다.

최악의 경우 주기는 (2^6)^3 = 262144까지 커질 수 있지만, 희망을 가지고 표를 채우다 보면 1행부터 3행까지와 13행부터 15행까지가 일치함을 발견할 수 있다. 따라서 1번 행부터 시작해서 매 12행마다 표가 반복된다.

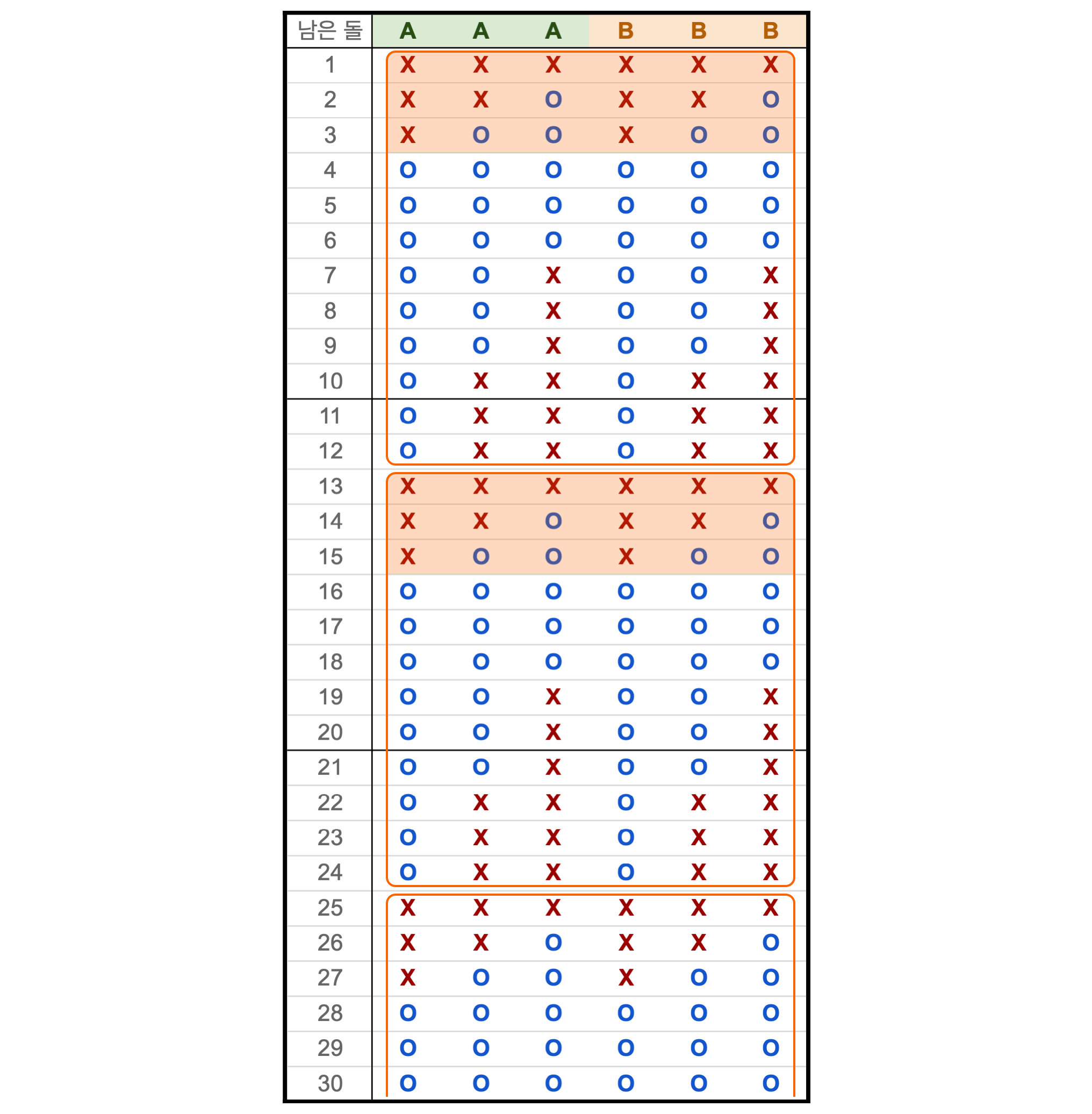
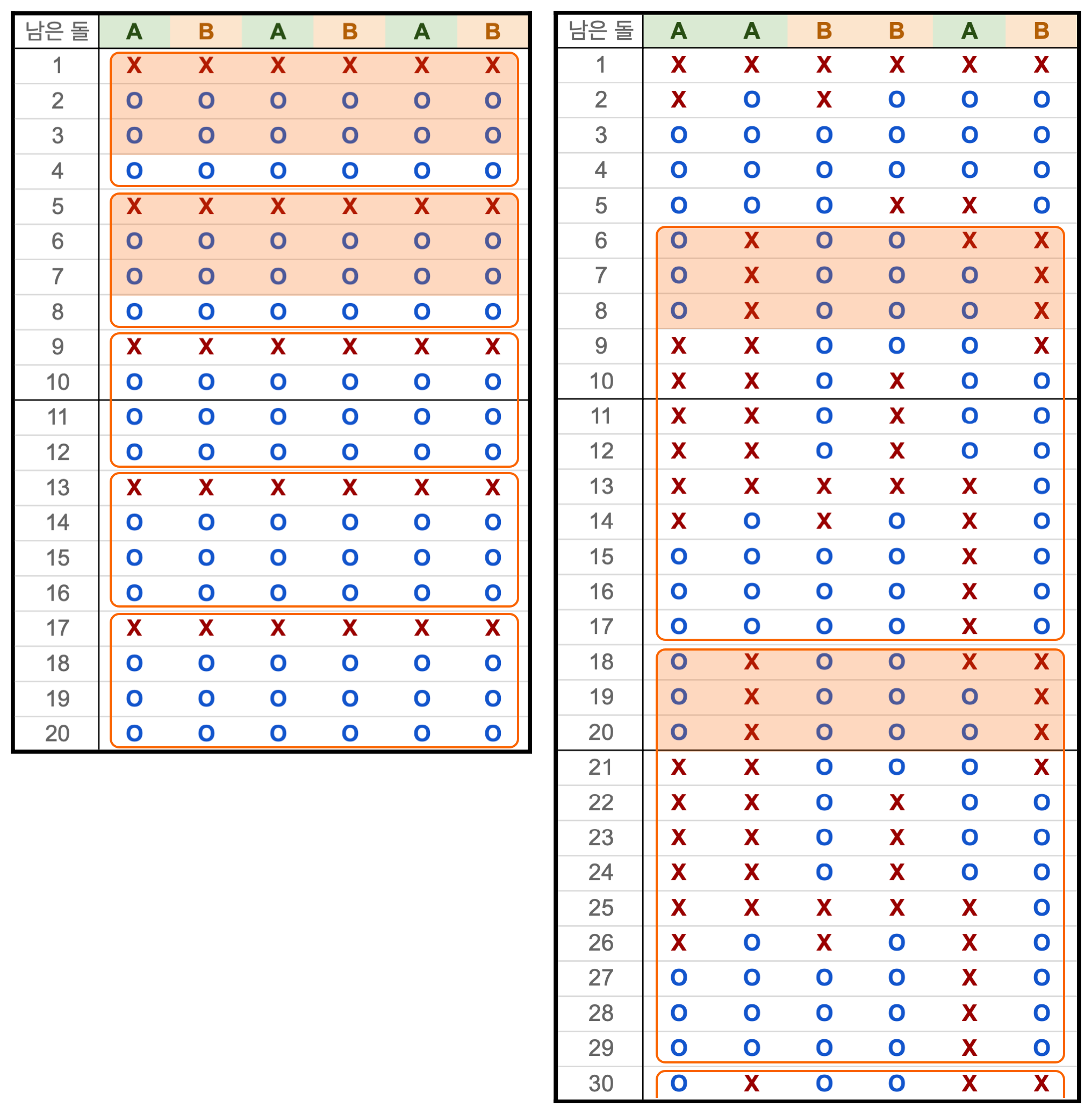
다른 배치들도 운 좋게 주기가 작다. 2번 배치는 1번 행부터 매 4행마다 표가 반복되고, 3번 배치는 6번 행부터 매 12행마다 표가 반복된다.

3번 배치의 표를 주목하자. 1000을 12로 나눈 나머지는 4니까, 4+12=16행을 보면 1000행의 승패 정보를 알 수 있다. 4행이 아니라 16행을 보는 이유는 6행부터 주기성이 생기기 때문이다. 16행을 살펴보면 다섯 번째 자리에 있는 플레이어가 턴을 가져갔을 때 패배한다. 즉, 동규는 해당 플레이어가 첫 턴을 가져가도록 자리를 배치하면 승리할 수 있다.

다른 배치들도 비슷하게 따져 보면, 어떤 플레이어가 첫 턴을 가져가든 승리하는 경우밖에 없으므로 동규의 팀이 이길 수 없다. 따라서, 시작하는 팀을 A, 동규의 팀을 B라고 했을 때, 첫 플레이어를 기준으로 ABAABB와 같이 배치하는 것이 동규가 승리할 수 있는 유일한 방법이다.

아래는 KPP 안진후님이 제공한 실제 승리 전략이다.

ABAABB 배치에서, 플레이어를 왼쪽부터 (가), (나), (다), (라), (마), (바)라고 부르자.

첫 바퀴에서 플레이어 (가)가 수 x개를 부르면 (나)는 4-x개를 불러서 총 4개의 수를 말한다. 이후 (다)와 (라)가 부른 수가 도합 s개라고 하자. s는 2 이상 6 이하이다.

s가 2, 3, 4 중 하나라면, (마)와 (바)는 도합 7-s개의 수를 말할 수 있다. 그러면 지금까지 4+7 = 11개의 수가 불렸다. 남은 수의 개수는 989개로, 12로 나눈 나머지가 5이다.

s가 5, 6 중 하나라면, (마)와 (바)는 도합 11-s개의 수를 말할 수 있다. 그러면 지금까지 4+11 = 15개의 수가 불렸다. 남은 수의 개수는 985개로, 12로 나눈 나머지가 1이다.

이제부터 플레이어 (가)가 x개를 부르면 플레이어 (나)는 4-x개를 부르고, (다)와 (라)가 y, z개를 부르면 플레이어 (마)와 (바) 4-y, 4-z개를 불러서 한 바퀴를 돌 때 도합 12개의 수를 부를 수 있다. 이를 반복하면 플레이어 (가) 차례에 5개 또는 1개의 수가 남은 상황이 된다.

(가) 차례에 1개의 수가 남은 경우 (가)가 마지막 수를 불러야 한다. 5개의 수가 남은 경우, (가)가 수 x개를 부르면 (나)는 4-x개를 불러서 (다)가 마지막 수를 부르게 만들 수 있다. 두 경우 모두 동규의 팀이 승리하게 된다.