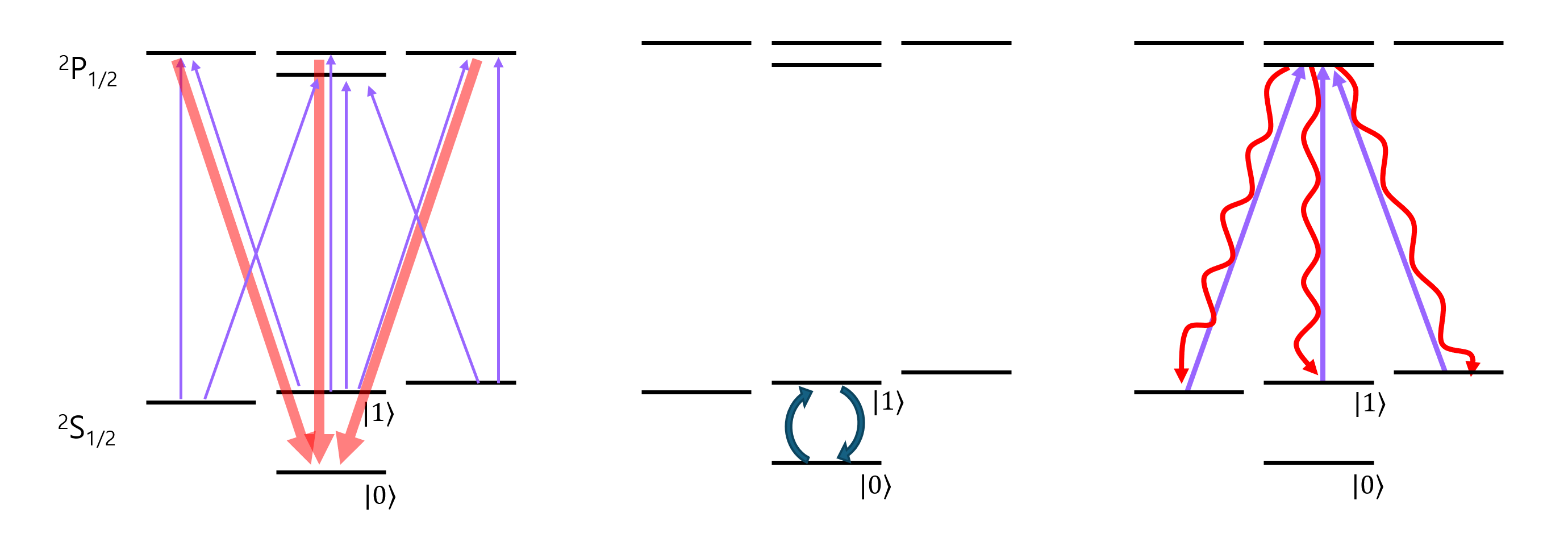[양자 컴퓨팅의 다양한 물리적 플랫폼] 이온 포획 양자컴퓨터: 기술적 원리와 향후 전망

Nothing exists except atoms and empty space; everything else is opinion
– Democritus

모든 세상은 원자로 이루어져 있다. 리처드 파인만^{Richard Feynman}은 1959년 그의 강연¹에서 원자를 하나하나 제어하는 궁극의 기술을 상상하고 이를 이용한 컴퓨터의 소형화를 이야기하였다. 이온 포획 기술은 이런 꿈의 기술을 실현하고, 원자 세계의 신비한 자연법칙-양자역학-을 기초로 작동하는 양자컴퓨터의 구현에 도전하고 있다. 본 원고에서는 이온 포획 양자컴퓨터 하드웨어 구현의 기술적 원리과 기술의 향후 전망에 대해 알아본다.

이온 포획과 이온 큐비트

이온 포획 기술의 시작은 1950년대로 거슬러 올라간다. 볼프강 폴^{Wolfgang Paul}과 한스 게오르그 드멜트^{Hans Georg Dehmelt}는 각각 RF^{Radio Frequency}를 사용하는 폴 트랩과 자기장을 사용하는 페닝 트랩을 개발하여, 이온이나 전자와 같은 전하 입자를 효과적으로 포획하는 기술을 개발하였다(이 업적으로 1987년 노벨 물리학상을 수상). 이러한 포획 기술은 고정밀 질량분석이나 전자의 자기장 모멘트 측정과 같은 정밀 측정 연구에 널리 활용되었다. 특히 분광학처럼 주파수 측정 분야에서는 에너지-시간 불확정성의 원리  \(\Delta E \Delta t > \hbar/2\) 때문에 긴 측정시간이 필수적인데, 빠르게 움직이는 기체나 원자 빔 샘플으로는 긴 측정시간을 확보할 수 없었다. 반면, 입자 포획 기술을 활용하면 샘플 입자를 고정하여 측정 시간을 증가시키고 측정의 정밀도를 크게 향상시킬 수 있다.

그 뒤 이온 포획 기술은 레이저 기술와 결합하면서 더욱 발전했다. 미국 국립표준기술연구소^NIST의 데이비드 와인랜드^{David Wineland} 박사와 그의 동료 연구진은 포획된 이온에 정밀한 레이저 냉각기술을 적용하여 포획된 이온의 운동을 바닥상태에 가깝게 냉각하는데 성공한다. 이렇게 에너지가 충분히 낮아진 이온은 양자 조화진동자^{Quantum harmonic oscillator}로 근사할 수 있으며, 바닥상태로 냉각된 이온은 여러가지 비고전적 양자 운동상태를 구현하는 기반이 되었다. NIST 연구진은 이 양자운동상태 제어 기술을 바탕으로 보손 양자계의 대표적인 비고전적 양자상태인 포크 상태^{Fock state}, 코히런트 상태^{Coherent state}, 그리고 위상이 다른 코히런트 상태들을 양자 중첩하여 만든 ‘슈뢰딩거 고양이 상태’ 등을 이온의 운동 상태를 이용해 구현하였고, 이 업적은 데이비드 와인랜드 박사가 2012년 노벨물리학상을 받는데 결정적인 역할을 했다. 한편, 1995년 이그나시오 시락^{Ignacio Cirac}과 피터 졸러^{Peter Zoller}는 이러한 이온 상태 제어 기술을 바탕으로 당시 주목받기 시작한 양자 컴퓨터를 이온 포획 시스템으로 실현할 수 있는 구체적인 방안을 제시함으로써, 이온 포획 기반 양자컴퓨터 연구의 길이 본격적으로 열리게 된다.

포획된 이온의 양자 상태는 원자 내 전자 오비탈에 의한 내부 상태^{internal state}와 포획장 안에서의 이온 운동에 따른 외부 상태^{external state}로 기술된다. 이온 포획에는 주로 Group-II 알칼리 토금속(베릴륨, 마그네슘, 칼슘, 스트론튬, 바륨)이나 이들과 유사한 최외각 전자구조를 가진 원소(예: 이터븀)가 사용되는데, 이 원자에서 전자를 하나 제거한 양이온 형태로 활용된다. 이들 원소는 이온화 에너지가 낮고, 이온화 이후 최외각 전자가 하나만 남는 단순한 전자 구조를 지니기 때문에 포획과 제어가 용이하다. Group-II 원자 이온들은 이러한 단순한 전자구조 덕분에 가장 간단한 수소 원자와 비슷한 전자 상태 구조를 가지며, 스핀-궤도 상호작용으로 인한 미세구조, 핵스핀과의 상호작용으로 인한 극미세구조, 그리고 외부 자기장에 의한 제만 분리가 관찰된다.

이 중 양자정보를 오래 유지할 수 있고 제어가 용이한 두 개 준위를 “이온 큐비트” 상태로 정의하며, 구체적으로 어떤 전자 상태를 큐비트로 삼느냐에 따라 극미세 큐비트, 제만 큐비트, 광학 큐비트 등으로 구분된다. 예를 들어 이터븀 이온은 S 오비탈 바닥상태의 극미세 분리가 단순해 극미세 큐비트로 주로 쓰이고, 칼슘 이온이나 스트론튬 이온은 S 오비탈 바닥상태에서 D 오비탈 준안정 상태로의 전이를 구현하기가 상대적으로 쉬워 광학 큐비트로 널리 이용된다.

한편 이렇게 정의된 이온 큐비트들은 서로 완전히 동일하다는 점이 중요하다. 자연계의 모든 원자는 기본적인 특성과 물리적 성질이 같으므로, 예컨대 10개의 이온을 포획했다면 모두 동일한 큐비트 특성을 지니게 된다. 이는 주변 환경 요인을 완벽히 제어하기 어려운 초전도 큐비트나 점결함 큐비트와 차별화되는 강점이며, 시스템 보정^calibration 등에서 발생하는 오버헤드를 크게 줄여 준다.

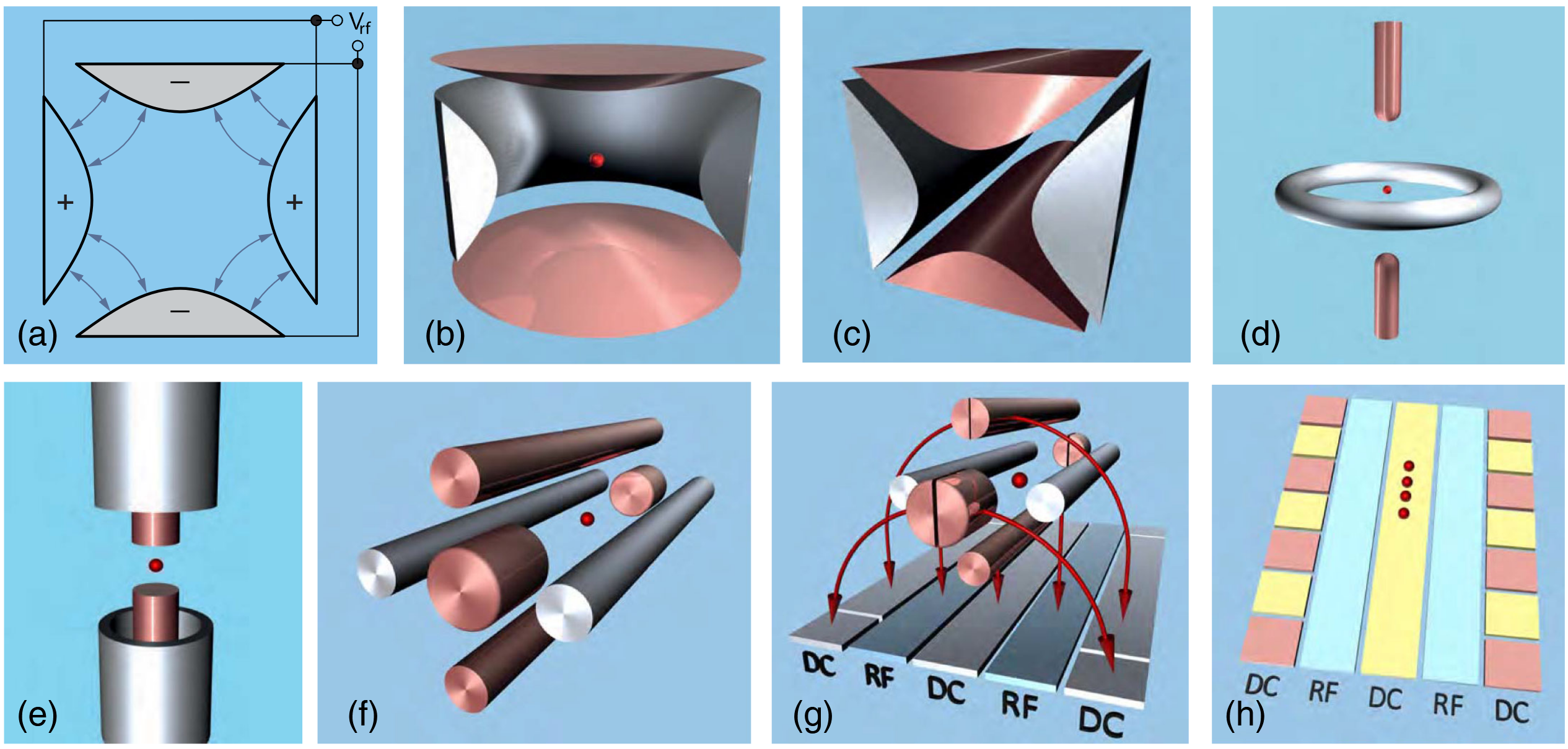
이온의 외부 상태는 3차원 공간에서 이온이 경험하는 포획 포텐셜에 의해 결정된다. 전하를 띤 입자는 전기포텐셜 하에서 전기장에 의해 힘을 받게 되지만, 언쇼 정리^{Earnshaw’s Theorem}에 따르면 정적인 전기포텐셜만으로는 3차원 공간에서 전하를 안정적으로 구속할 수 없다. 그러나 시간에 따라 진동하는 전기장에서는, 전하 입자가 전기장 세기의 공간적 분포에 따라 비대칭적인 힘을 받아 전기장이 약한 쪽으로 밀려나는데, 이를 ‘폰데로모티브 힘^{ponderomotive force}’이라 한다. 폴 트랩은 이러한 진동하는 전기장을 이용해 이온을 포획하며, 포획된 이온은 전기장 세기가 0이 되는 지점 부근에 모이게 된다.

한편, 포획장 안에 여러 이온이 함께 존재하면 전하를 띈 이온간에 전기적 척력이 작용하여 결정 구조를 형성한다. 이 결정 구조의 형태는 포획 포텐셜의 공간 분포에 따라 다양하게 나타나며, 1차원 체인부터 3차원 결정 형태까지 다양한 배열을 형성한다. 또한 이때 이온들의 진동 운동 상태는 전기적 상호작용에 의해 ‘포논^phonon’이라 불리는 집단 진동 상태로 재정의된다.

정리하자면, 포획장 안에 놓인 N개의 이온은 각각 내부 상태(큐비트) N개와 외부 상태(포논 모드) 3N개로 구성되며, 전체적인 양자 상태는 이 두 부분의 텐서곱으로 표현된다. 이런 스핀-보존^spin-boson 계는 공진기 QED^{cavity QED}처럼 다른 양자 시스템과도 유사한 물리적 특성과 현상을 공유한다. 이온 포획 범용 양자컴퓨터의 구현에서는 통상적으로 내부 상태에 양자정보를 저장하고, 외부 상태는 큐비트 연산을 보조하는 용도로 활용된다. 한편 최근에는 이를 뒤집어서 외부 상태로 직접 연산을 수행하고, 내부 상태는 보조로 활용하는 연구나, 스핀-보존 양자계 전체를 이용한 양자 시뮬레이션 같은 새로운 접근 방법도 활발히 진행되고 있다.

범용 양자 컴퓨팅 연산의 구현

큐비트 기반 범용 양자컴퓨터의 연산(범용 양자 회로에 관해서는 손영익 교수님의 글 을 참조) 을 구현하기 위해서는 큐비트의 상태 초기화, 단일 큐비트 게이트와 얽힘 게이트와 같은 논리 게이트의 구현, 그리고 마지막으로 큐비트 상태 측정이 필수적이다.

큐비트 상태 초기화 : 포획된 이온은 주로 S 오비탈 바닥상태에 존재하지만, 제만 분리나 극미세 분리 등에 의해 바닥상태 내에서도 여러 양자상태에 걸쳐 분포할 수 있고, 특정 양자상태로 이온을 초기화하려면 ‘광펌핑^{optical pumping}’ 과정을 거쳐야 한다. 광펌핑을 구현하기 위해서는 레이저를 이용해 바닥상태의 전자를 여기시키고, 자발 방출을 통해 다시 바닥상태로 돌아오도록 하는 과정을 반복해야 한다. 이때 레이저의 편광과 주파수를 적절히 조정해 하나의 양자상태를 다시 여기되지 않는 ‘암흑 상태^{dark state}’를 만들면, 전자는 점차 암흑 상태에 머무를 확률이 높아져 결국 특정 양자상태로 고정된다.

얽힘 연산 등을 수행하기 위해서는 이온의 내부상태뿐 아니라 외부상태도 초기화해야 한다. 먼저 ‘도플러 냉각^{Doppler cooling}’을 통해 이온 온도를 mK 수준으로 빠르게 낮출 수 있지만, 이 방식만으로는 외부상태를 순수한 바닥상태로 만들기는 어렵다. 이를 보완하기 위해 사용하는 방법이 ‘사이드밴드 냉각^{sideband cooling}’이다. 사이드밴드 냉각에서는 레이저를 이용해 이온 외부상태의 들뜬 에너지를 이온 내부상태로 전환한 뒤 광펌핑으로 내부상태를 다시 초기화하는 과정을 반복한다. 이 과정을 통해 외부상태 에너지는 점차 낮아져 최종적으로 바닥상태에 가깝게 도달한다. 내부상태와 외부상태가 모두 준비가 완료되면, 비로소 이온 큐비트에 대한 연산을 시작할 수 있다.

논리 게이트 구현 : 이온 큐비트의 양자 게이트 구현에는 전자기파에 의한 공진현상이 사용된다. 큐비트의 전이 주파수와 동일한 주파수의 전자기장이 이온 큐비트에 가해지면 라비 진동^{Rabi oscillation}이 유도되어 초기화되었던 이온 내부의 양자상태가 변화한다. 이 라비 진동의 길이와 위상을 제어하면 단일 큐비트의 게이트를 구현하는 것이 가능하고, 이는 비단 이온 큐비트 이외에 다른 큐비트 플랫폼에서도 보편적으로 사용되는 방식이다.

앞서 이야기한 여러 이온 큐비트 정의에 따라 사용되는 전자기파의 주파수도 달라진다. 극미세 큐비트나 제만 큐비트는 큐비트 전이 주파수가 낮아(<수십 GHz), RF 신호나 마이크로파를 사용하거나 두 결맞은 레이저의 맥놀이 주파수를 큐비트 전이와 일치시키는 ‘라만 전이^{Raman transition}’가 사용되기도 한다. 한편 광학 큐비트는 큐비트 전이가 가시광-적외선 영역에 있으므로, 제어 전자기파 역시 광학 레이저로 구현된다. 모든 경우에서 제어 전자기파 위상의 안정성은 게이트 정밀도와 여러 차례 반복되는 게이트 사이의 결맞음을 유지하는 데 매우 중요한 역할을 한다. 이를 위해서는 잘 제어된 전자기파 또는 매우 좁은 선폭의 레이저가 필수적이다.

얽힘 게이트는 좀 더 복잡한 과정을 수반한다. 일반적으로 포획된 여러 이온 큐비트는 내부 상태 간 직접적인 상호작용이 매우 약해, 서로 얽힌 상태가 자연스럽게 생성되지 않는다. 반면, 이온의 외부 운동 상태는 전기적 상호작용에 의해 서로 강하게 상호작용하고 있으며, 하나의 이온이 진동하면 다른 이온도 따라 진동하게 된다. 따라서 얽힘을 만들기 위해서는 이러한 이온 외부 상태들의 전기적 상호작용을 활용하여 이온 큐비트간의 양자 상호작용을 구현한다. 앞서 이야기한 ‘사이드밴드 냉각’에서와 동일하게 이온에 가해지는 레이저의 주파수를 제어하여 내부 상태와 외부 상태 간 결맞은 상호작용을 유도할 수 있으며, 이를 통하여 이온이 내부상태에 따라 다른 방향의 힘(상태-의존 힘, Spin-dependent force)을 받도록 조작하는 것이 가능하다. 얽힘 게이트는 이 상호작용 과정을 섬세하게 제어하여, 최종적으로는 내부·외부 상태가 얽히지 않도록 분리하고 이온 큐비트의 내부큐비트 상태들끼리만 얽혀 있는 상태를 얻는다. 이때 외부 상태는 얽힘 과정에 참여하되, 최종 양자 상태에서는 다시 초기상태로 돌아오기에 “퀀텀 버스^{quantum bus}”라고 불리기도 한다.

최초로 제안된 이온 얽힘 게이트 프로토콜은 1995년의 ‘Cirac-Zoller 게이트’이지만 이 방법은 이온 외부 상태가 완전히 바닥상태에 있지 않으면 게이트 신뢰도가 급격히 떨어져, 실험적 검증은 2003년에야 이루어졌다. 대신 1999년에 제안되고 2000년에 실험적으로 구현된 ‘Mølmer–Sørensen^MS 게이트’가 이온 얽힘 게이트의 첫 실증 사례가 되었다. MS 게이트는 초기 외부 상태가 완전한 바닥상태가 아니어도 적용가능한 프로토콜로 상태-의존 힘에 의해 발생하는 이온 큐비트 상태의 기하학적 위상을 활용한다. 이 게이트 프로토콜은 현재까지도 가장 높은 신뢰도를 달성한 방식 중 하나로, 다양한 이온 포획 시스템에서 널리 활용되고 있다.

큐비트 상태 측정 : 양자 연산이 끝난 뒤 이온의 상태는 형광 검출^{Fluorescence detection} 기법으로 측정한다. 이는 이온에 레이저를 쪼인 뒤 산란된 형광 신호를 측정하여 큐비트 상태를 알아내는 방식으로, 초기화 과정과 비슷하게 특정 상태만 여기시키도록 레이저를 제어하여 높은 측정 정밀도를 구현한다. 한편 일부 이온 원소에서는 측정 과정 중 큐비트 상태가 섞일 우려가 있는데, 이때는 큐비트 중 하나를 암흑 상태로 이동시킨 뒤 형광을 측정하는 ‘전자 쉘빙^{electron shelving}’ 기법을 활용하여 높은 측정 정확도를 얻을 수 있다.

이온 포획 양자컴퓨터의 확장

그렇다면 이렇게 범용 양자컴퓨터에 필요한 모든 요소기술을 구현했다고 해서, 곧바로 실용적인 이온 포획 양자컴퓨터가 완성되는 걸까? 유감스럽게도 그렇지 않다. 이온 큐비트의 개수가 늘어날수록, 지금까지 살펴본 요소기술들을 단순히 확장하기가 점점 어려워지기 때문이다.

가장 직관적인 확장 방식은 하나의 포획장에 여러 이온 큐비트를 동시에 포획하는 것이다. 예를 들어 선형 폴 트랩^{linear Paul trap}은 포획장을 비대칭적으로 구성하여 1차원 체인 형태로 이온을 정렬하기가 비교적 쉽다. 이렇게 늘어선 이온들은 서로 수 마이크로미터^μm 간격을 두고 배열되는데, 각각을 강하게 집속된 레이저로 개별 조사하면 개별 양자상태를 제어할 수 있다. 얽힘 게이트의 경우도 비슷한 방식으로, 두 이온에 동시에 수 마이크로미터 수준으로 집속된 레이저를 조사함으로써 구현한다. 이때 모든 이온은 전기적 상호작용을 통해 하나의 집단 진동(포논 모드)으로 묶여 있으므로, 임의의 두 이온 간에도 동일한 외부 상태(포논)를 매개로 얽힘을 생성할 수 있다. 이러한 특징 덕분에, 선형 이온 체인 내에서는 임의 큐비트 간 얽힘 게이트가 구현 가능한 ‘All-to-all’ 연결성이 가능하다는 장점이 있다.

그러나 이런 방식으로 이온 큐비트를 확장하는 데는 분명한 한계가 있다. 먼저 1차원 체인 형태를 만들려면 포획장의 한쪽 방향을 약하게 구속하는 비대칭적 포획장을 구현해야 하는데, 이온 수가 많아질수록 축 방향 포텐셜이 약해져 안정적으로 이온을 포획하기가 점점 어려워진다. 또한 긴 이온 체인에서는 양끝에 있는 이온 간 상호작용 세기가 약해지고, 동시에 포논 모드 간 주파수 간격도 좁아져 개별 제어가 까다로워진다. 실제로 많은 이온 트랩 연구자들은 단일 체인에서 효과적으로 제어 가능한 이온 큐비트 수를 적게는 50개에서 많게는 200개 정도로 보고 있다. 이러한 문제점을 해결하기 위해 광자를 이용한 모듈간 연결 확장방식이나, ‘이온 셔틀링^{ion shuttling}’을 활용한 확장 방식 등이 제안되고 있다.

 

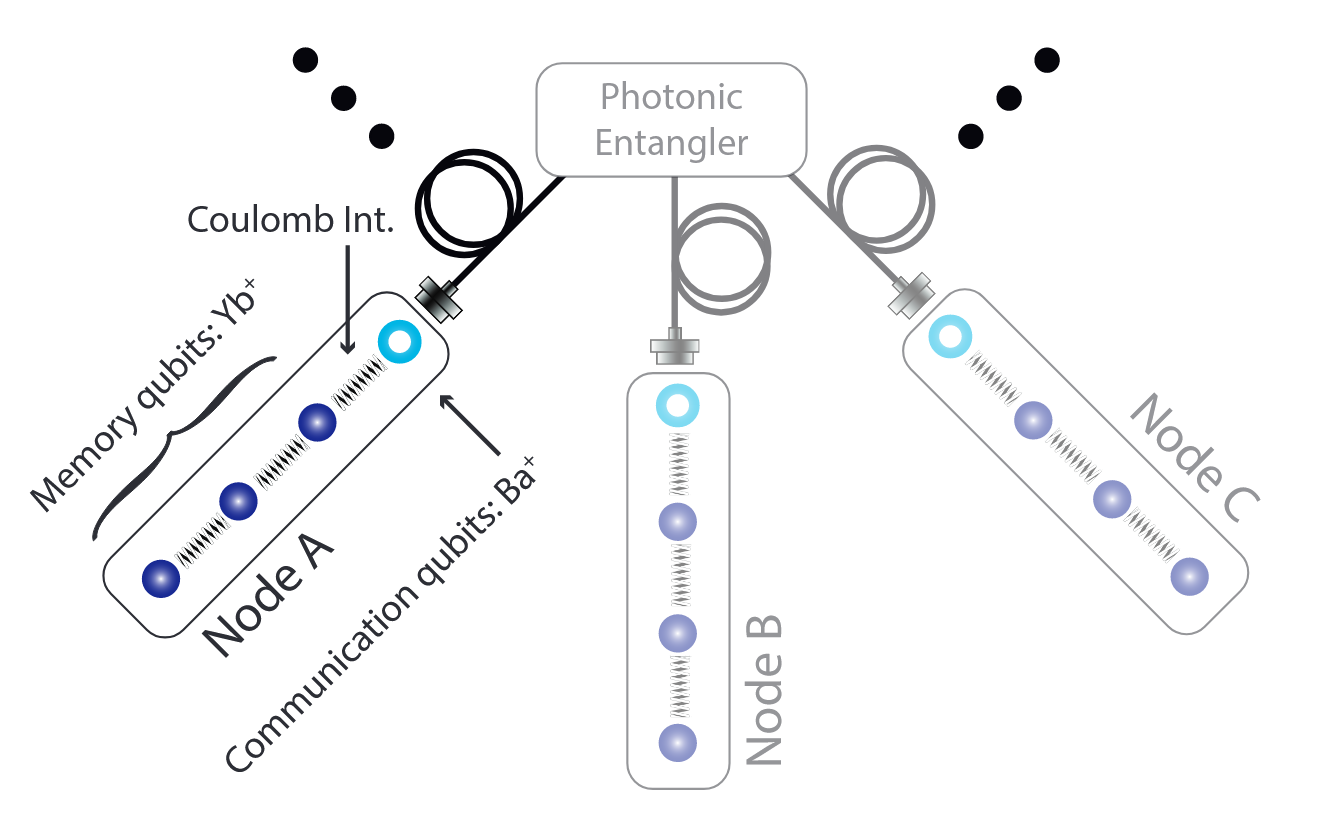
광자를 이용한 확장 방식은 이온 큐비트뿐만 아니라 초전도 큐비트, 점결함 큐비트 등 다양한 플랫폼에서도 공통적으로 연구되고 있는 방법이다. 이온 큐비트의 경우, 여기 상태 이온이 자발 방출을 일으킬 때 이온 내부 상태와 방출된 광자 상태가 양자 얽힘을 형성하며, 이 광자를 매개로 원거리 이온 간 얽힘을 구현할 수 있다. 광자를 활용하는 연결 방식은 광스위치 등의 광학 소자를 통해 여러 모듈 간 얽힘을 빠르게 확장할 수 있다는 장점이 있다.

이때 핵심 요소 기술은 이온에서 방출된 광자를 효율적으로 수집하고 양자 정보를 전송·처리할 수 있는 ‘이온-광 양자 인터페이스’이다. 이를 위해 높은 개구수를 가진 대물렌즈를 이용하는 광학계나, 이온을 공진기에 결합시키는 방법 등이 활발히 연구되고 있다. 원거리 이온 간 양자 얽힘을 생성하기 위해서는 두 쌍의 ‘이온-광자 얽힘’이 필요하지만, 현재 이온-광자 얽힘 생성 효율이 최대 약 2% 수준에 머무르고 있어 이를 개선하는 것이 주요 과제로 남아 있다.

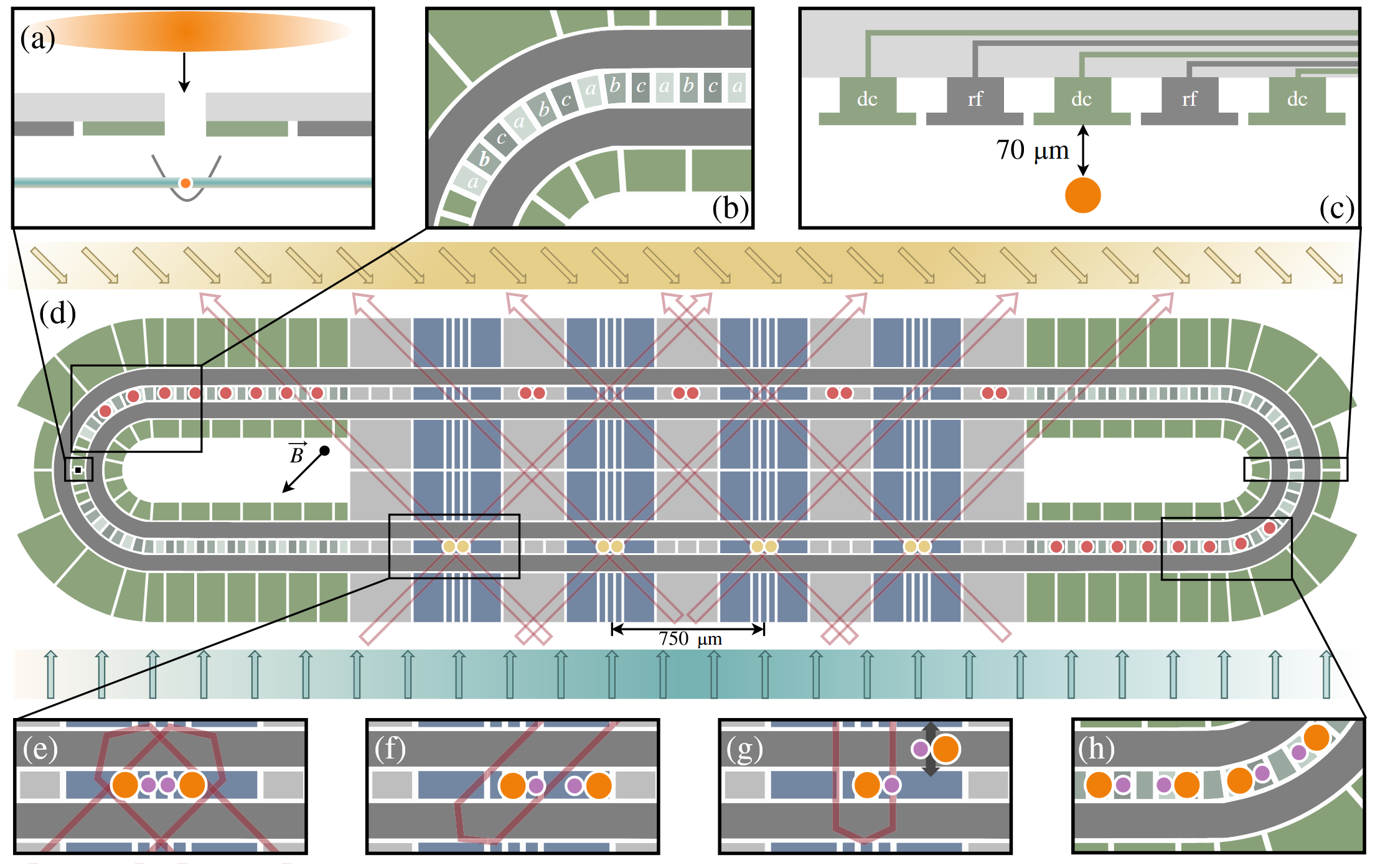
또 다른 접근 방식으로는, 이온을 하나의 체인 형태로 포획하지 않고 개별 포획 위치를 제어해 큐비트 개수를 확장하는 ‘QCCD^{Quantum Charge-Coupled Device} 아키텍처’가 있다. 발전된 이온 트랩에서는 여러 개의 작은 DC 전극을 통해 포획 포텐셜을 정교하게 제어함으로써, 이온의 물리적인 이동(이온 셔틀링)이 가능해졌다. 이를 활용하면, 필요한 순간에 이온 위치를 재배치한 뒤 얽힘 게이트를 수행함으로써 큐비트 간 높은 연결성을 유지하면서도 전체 큐비트 수를 늘릴 수 있고, 얽힘 게이트의 충실도 역시 높은 수준으로 유지할 수 있다. 다만 이온을 셔틀링하는 과정에서 이온 외부 상태가 영향을 받을 수 있어 추가적인 냉각에 시간이 소요되며, 셔틀링 속도가 느려 전체 연산 속도가 제한되는 점은 해결해야 할 주요 과제로 남아 있다.

여기서 강조하고 싶은 점은, 데이터 큐비트를 직접 이동하거나 다른 큐비트를 활용하는 방법이 양자 컴퓨터에서는 어느 정도 필수적이라는 사실이다. 양자 정보는 본질적으로 복사할 수 없으므로(양자 복제 불가능 정리), 우리가 고전적인 신호전달에 사용하는 전선으로 양자정보를 전달할 수 없다. 물리적으로 멀리 떨어진 두 큐비트를 연산하기 위해서는 어느 한쪽의 정보를 다른 쪽으로 옮길 필요가 있으며, 이러한 관점에서 보면 고정된 큐비트 배열에 비해 실제로 큐비트를 물리적으로 이동할 수 있는 플랫폼이 양자 정보 처리에 더 효율적일 수도 있다.

이온 포획 양자컴퓨터를 개발하는 여러 기업들이 서로 다른 확장 방식을 택하고 있다는 점도 주목할 만하다. 예를 들어 IonQ는 단일 체인 프로세서에 광자를 이용한 모듈 간 연결 방식을 결합하고, Quantinuum과 Oxford Ionics는 큐비트 셔틀링을 기반으로 확장 방안을 모색하고 있다. 물론 이 두 접근법은 상호 보완적으로 결합될 수 있으며, 이러한 아키텍처 설계에 관한 이론 연구도 활발히 진행 중이다.

향후 전망

이온 포획 양자컴퓨팅 기술은 지난 몇 년간 스타트업 등 산업계의 적극적인 참여로 연구 개발이 더욱 가속화되고 있다. 2024년에 발표된 결과에 따르면, 상용 시스템에서 얽힘 게이트의 충실도가 99.9% 이상 달성되었고, 56큐비트 규모의 양자 회로 랜덤 샘플링까지 구현되는 등, 성능과 시스템 규모 양 측면에서 눈에 띄는 성과가 있었다. 이처럼 단순히 시스템 성능을 개선하는 데 그치지 않고, 새로운 접근법들도 다양하게 시도되고 있는데, 여기서는 그중 몇 가지를 간략히 살펴보고자 한다.

첫째로, 다양한 형태의 이온 트랩 개발이 활발히 진행되고 있다. 2000년대 이후로는 이온 포텐셜을 더 정밀하게 제어하고 이온 셔틀링을 구현하기 위해 주로 평면형 칩 트랩이 연구돼 왔다. 최근에는 이러한 칩 트랩에 광도파로, 회절 격자, 광검출기 같은 집적 광학 소자나 근거리 자기장을 생성하기 위한 전선을 통합함으로써, 이온을 한층 정밀하게 제어할 수 있는 기술이 함께 결합되고 있다. 또 레이저 기반 미세 유리 가공 기술이나 3차원 미세 프린팅 기술 등을 활용해, 더욱 다양한 기능을 갖춘 이온 트랩을 제작하려는 연구도 이어지고 있다. 이렇게 새롭게 개발되는 트랩들은 단순히 시스템을 소형화 뿐만 아니라, 확장성 측면에서도 커다란 이점을 제공할 것으로 기대된다.

둘째로는 ‘확장된 큐비트 매핑’에 대한 연구가 활발하다. 이온 원자의 전자 구조는 매우 복잡해, 결맞음 시간이 충분히 긴 다양한 상태가 존재한다. 2021년에 발표된 이른바 “OMG Blueprint” 논문에서는 광학^Optical 큐비트, 준안정^Metastable 큐비트, 바닥^Ground 큐비트² 간의 매핑을 동적으로 전환하며 양자 컴퓨팅을 구현하는 방법을 제안해 큰 주목을 받았다. 이후 준안정 큐비트를 활용한 ‘지움^erase 오류 변환’ 기법이 등장해 오류 정정에도 효과적임이 확인되었다. 또한 하나의 이온에서 2개 이상의 양자 상태를 사용하여 ‘큐디트^qudit’로 운용하는 방안도 연구되고 있다. 주로 제만 분리 상태를 이용해, 동일한 수의 이온에서 더 많은 양자 정보를 압축해 저장하려는 시도가 대표적이다.

앞으로도 이처럼 다양한 접근이 서로 보완적으로 시도됨으로써 이온 포획 양자컴퓨팅 분야는 더욱 폭넓고 풍부한 발전을 이룰 것으로 기대된다.

맺음말

이온 포획 기술은 지난 수십 년간 눈부시게 발전해 왔으며, 관련 연구 커뮤니티도 급속도로 성장하여 현재 전 세계에 100곳이 넘는 이온 포획 연구 그룹이 활발히 활동 중이다. 이들의 연구 주제는 원자물리나 정밀 측정과 같은 기초 물리학 분야부터, 실제 작동 가능한 소자를 만들기 위한 공학적 접근과 아키텍처 설계까지 폭넓은 영역을 아우른다. 무엇보다 이 분야의 가장 큰 매력은 원자 하나하나를 직접 보고 양자상태를 직접 제어하는 독특한 경험을 할 수 있다는 점이라고 생각한다. 이온 포획을 연구하는 한 연구자로서, 원자로 쌓아올린 꿈의 기계가 실용화되는 그날을 벅찬 마음으로 상상해본다.