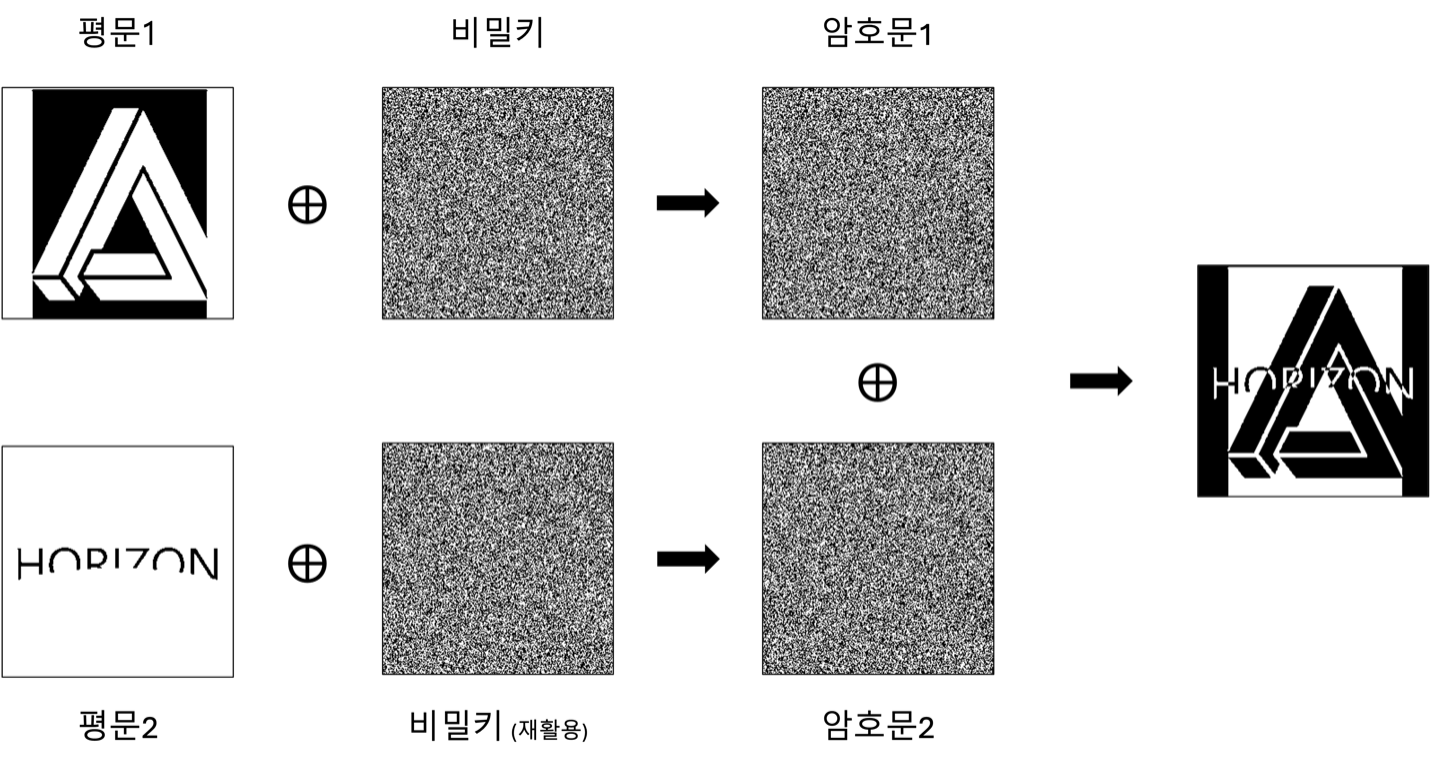현대암호학의 태동 [2]: 섀넌의 정보이론적 안정성

섀넌과 정보이론

20세기 인물인 클로드 섀넌^{Claude Shannon; 1916~2001}은 21세기 과학기술의 아버지라 불릴 만하다. 부울 대수^{Boolean Algebra}와 전기회로 사이의 대응 관계를 통해 디지털논리회로 이론을 정립한 그의 연구논문 [1] 은 역사상 가장 중요한 “석사” 학위논문으로 평가받는다. 섀넌은 인공지능 분야의 탄생에도 기여했다. 체스를 두는 컴퓨터 프로그램에 관한 논문 [2] 을 발표했는데, 당시

전 세계에 컴퓨터가 10대도 채 존재하지 않던 시점에서 그가 설정한 아젠다가 IBM의 Deep Blue 그리고 딥마인드의 알파고로 이어진다는 점은 매우 흥미롭다. 또한 그는 학습을 통해 미로를 탈출하는 로봇 쥐를 만들어 선보였고 [그림. 2], 1956년에는 다트머스 회의^{Dartmouth Workshop}를 공동조직^co-organize하며 인공지능이라는 학문 분야의 출발을 알렸다. 

그래도 무엇보다도 섀넌은 “정보이론^{information theory}” [3] 의 창시자로 가장 잘 알려져 있으며, “비트^bit”라는 용어를 처음 공식적으로 사용한 인물이기도 하다. 당시에는 전보는 텍스트를, 전화는 음성을, 텔레비전은 영상을 각각 다른 방식으로 전송하고 있었으나, 이를 통합하는 이론적 토대는 존재하지 않았다. 특히, 잡음이 있는 환경에서 효율적으로 정보를 전달하는 문제는 모든 통신 매체에서 공통으로 중요한 과제였음에도 불구하고, 이에 대한 체계적인 이해는 부족한 상태였다. 섀넌의 정보이론은 이러한 정보통신 문제를 통합적으로 다루는 이론으로, 기존의 잡음 자체를 최소화하려는 하드웨어적 접근에서 벗어나, 잡음이 존재하는 환경에서도 효율적인 통신이 가능하도록 그 원리와 한계를 탐구하는 소프트웨어적 접근으로의 패러다임 전환을 이끌었다. 이러한 연구를 바탕으로 데이터압축, 오류정정코드 등 오늘날 정보사회에서 필수적인 개념들이 탄생했다.

섀넌은 이 과정에서 정보를 정량적으로 측정하는 개념인 “정보량^{Shannon information}”을 정의했다. 그는 개별 메시지의 통사론적 그리고 의미론적 요소를 배제하고 정보량을 “놀라움의 정도^surprisal”로 해석했다. 더 정확히는 확률사건 \(x\)의 정보량을 \(I(x)=-\log_2[\Pr(x)]\)으로 정의하고, 이 정의가 본질적으로 유일한 선택임을 증명했다. 섀넌의 정의는 직관적으로도 자연스럽다. 거의 항상 발생하여 놀랍지 않은 정보, 예를 들어 특정 로또 번호가 1등이 아니라는 정보는 정보량이 작다고 보는 것이 타당하다. 반면 매우 드물게 발생하여 놀라운 정보, 가령 특정 로또 번호가 1등이라는 정보는 정보량이 크다고 해석하는 것이 합리적이다.

섀넌의 혁신은 정보량을 정의할 때 개별 메시지가 아닌 메시지의 확률분포를 고려했다는 점에 있다. 혹자의 표현¹을 빌리자면, 섀넌에게 “정보”란 ‘실제로 전달된 내용’보다 ‘전달될 수도 있었던 내용’과 더욱 밀접한 관련이 있다. 이러한 관점은 다양한 통신 매체를 아우르는 통합된 이론을 구축하는 데에 핵심적인 역할을 한다. 각 통신 매체마다 메시지를 표현하는 방식이 다르며, 개별 메시지에는 불필요한 중복^redundancy이 존재할 수 있다. 따라서 정보량을 보편적으로 정의하기 위해서는 메시지의 구체적인 표현방식에서 벗어날 필요가 있었다.

섀넌은 정보량을 바탕으로 어떤 확률변수의 평균정보량을 나타내는 엔트로피^entropy와 두 확률변수 간의 정보 공유 정도를 측정하는 상호정보량^{mutual information} 등을 정의하고, 이들을 바탕으로 이론을 전개해 나갔다. (즉 상호정보량은 한 변수를 관측했을 때 다른 변수에 대해 평균적으로 얻을 수 있는 정보의 양을 의미한다.) 보다 자세한 내용은 조정효 교수님의 Horizon 글 <머신러닝과 정보이론: 작동원리의 이해>에서도 확인할 수 있다.

정보이론적 안전성

섀넌은 제2차 세계대전 당시 미국 벨 연구소^{Bell Labs}에서 국방 연구개발에 참여하며 암호학에도 큰 족적을 남겼다. 1945년 전쟁이 끝난 직후 섀넌은 연구 내용을 정리하여 벨 연구소 내부에 <A Mathematical Theory of Cryptography> [4] 라는 제목의 비망록을 작성했으나 기밀로 지정되었다. 이후, 시간이 흘러 1949년에 해당 연구는 <Communication Theory of Secrecy Systems> [5] 라는 제목의 논문으로 세상에 공개되었다. 

논문은 다양한 내용을 다루고 있지만 그중 가장 중요한 업적은 암호의 안전성에 대한 최초의 수학적 정의를 제시했다는 점이다. 기존의 암호학은 암호설계자와 암호해독가 사이의 끊임없는 공방 속에서 주먹구구식으로 발전해 왔으나, 섀넌은 이를 탈피하여 암호의 안전성을 엄밀히 정의하는 문제를 제기하고 이에 대한 자연스러운 답을 제시했다. 섀넌은 암호의 안전성을 ‘비밀키가 주어지지 않은 상태에서는 암호문이 평문의 “정보”를 전혀 담고 있지 않는다’는 것으로 정의했다. 동어 반복처럼 들릴 수도 있지만, 중요한 점은 암호의 안전성이 이전까지 한 번도 수학적으로 정의된 적이 없었으며, 반면 여기서 말하는 “정보”는 이미 정보이론에서 엄밀히 정의된 개념이라는 것이다. 예상했겠지만 현대에는 이를 정보이론적 안전성^{information theoretic security}이라고 부른다.

더 정확한 설명을 위해 표기법을 도입하자. 하나의 암호화 방식^{encryption scheme}은 다음 세 가지 알고리즘으로 구성된다.

– 키생성알고리즘 \(\mathsf{KeyGen}\)은 키공간 \(\mathcal{K}\)에서 비밀키 \(k\)를 정해진 확률분포에서 뽑는다.
– 암호화알고리즘 \(\mathsf{Enc}\)는 비밀키 \(k\)와 메시지공간 \(\mathcal{M}\)의 원소 \(m\)을 입력으로 받아, 암호문공간 \(\mathcal{C}\)의 원소 \(c\)를 출력한다.
– 복호화알고리즘 \(\mathsf{Dec}\)는 비밀키 \(k\)와 암호문공간 \(\mathcal{C}\)의 원소 \(c\)를 입력으로 받아, 메시지공간 \(\mathcal{M}\)의 원소 \(m\)을 출력한다.

이때 “올바른” 암호화 방식이라면 임의의 \(k\in \mathcal{K}\)와 \(m\in \mathcal{M}\)에 대해 \(\mathsf{Dec}_k(\mathsf{Enc}_k(m))=m\)이 항상 성립해야 한다. 즉 암호화 후 복호화하면 언제나 원래 메시지를 복구할 수 있어야 한다는 것이다.

이제 안전성을 정의하기 위해 메시지를 표현하는 확률변수 \(M\)과 그에 따른 암호문의 확률변수 \(C\)를 고려하자. 더 정확히 \(C\)는 \(M\)의 확률분포를 따르는 \(m\)에 대해 (1) \(\mathsf{KeyGen}\)을 통해 비밀키 \(k\)를 생성하고 (2) 암호화 과정을 거쳐 \(c=\mathsf{Enc}_k(m)\)으로 정의되는 \(c\)를 따르는 확률변수이다. 이때 정보이론적 안정성은 확률변수 \(M\)과 \(C\)의 상호정보량이 0이라는 것으로 정의할 수 있다. 한편 두 확률변수의 상호정보량이 0이라는 것이 두 확률변수가 독립이라는 것과 동치라는 사실을 사용하면 정의를 다음과 같이 풀어 쓸 수 있다. 

\(\Pr[M=m]=\Pr[M=m ~\mid~ C=c]\)

이는 암호문이 주어진 메시지의 사후확률^{posterior probability}이 사전확률^{prior probability}과 다름없음을 의미하며, 즉 공격자 입장에서 암호문을 보고도 평문에 대한 추가적인 정보를 얻을 수 없다는 것을 뜻한다.

원타임패드

섀넌의 정의는 정말 깔끔하고 자연스럽다. 그렇다면 다음으로 떠오르는 질문은 과연 이 정의를 만족하는 암호가 실제로 존재하느냐는 것이다. 정답은 “존재한다”이다. 바로 원타임패드^{One-Time Pad}라는 암호다. 원타임패드는 1919년 미국 AT&T의 길버트 버넘^{Gilbert Vernam; 1890~1960}이 관련 내용에 대해 특허를 등록하면서 버넘 암호^{Vernam Cipher}라고도 불리지만 훨씬 전인 1882년 기록에도 유사한 방식이 등장한다.

원타임패드는 다음 알고리즘들로 구성된다. 일반성을 잃지 않고 메시지공간이 길이 \(n\)짜리 비트열로 구성되어 있다고 하자. 즉 \(\mathcal{M}=\{0,1\}^n\). 아래에서 \(\oplus\)는 비트 간 배타적 논리합^{bitwise exclusive or; bitwise XOR}을 의미하며, 이는 각 비트를 더한 후 2로 나눈 나머지를 취하는 연산이다.²  

– 키생성알고리즘 \(\mathsf{KeyGen}\)은 키공간 \(\mathcal{K}=\{0,1\}^n\)에서 비밀키 \(k\)를 균등확률분포에 따라 뽑는다.
– 암호화알고리즘 \(\mathsf{Enc}\)는 비밀키 \(k\)와 메시지 \(m\in\mathcal{M}\)을 입력으로 받아, \(c=k\oplus m\)를 출력한다.
– 복호화알고리즘 \(\mathsf{Dec}\)는 비밀키 \(k\)와 암호문 \(c\in\{0,1\}^n\)를 입력으로 받아, \(m=k\oplus c\)를 출력한다.

즉 원타임패드는 평문을 난수(비밀키)로 덮는 매우 단순한 방식의 암호이다. 원타임패드의 암호화 과정은 아래 [그림 3]을 통해 직관적으로 이해할 수 있다. 원타임패드가 올바른 암호화 방식이라는 것은 \(k\oplus(k\oplus m)=m\)이 항상 성립함을 통해 쉽게 확인할 수 있다. 정보이론적 안전성을 만족한다는 사실은, 메시지의 분포와 상관없이 비밀키가 균등확률분포를 따르기 때문에 암호문도 균등확률분포를 따른다는 사실과 베이즈 정리^{Bayes’ Theorem}로부터 쉽게 도출된다. 

원타임패드의 한계

완벽한 안전성을 자랑하고 복호화 과정이 매우 간단하여 별도의 기계가 필요 없다는 점에서 원타임패드는 한 때 간첩 활동과 같은 특수한 상황에서 활용되기도 했지만, 실용성에는 큰 한계가 있다. 문제는 비밀키의 길이가 메시지의 길이만큼 길어야 한다는 점이다. 이에 따라 대량의 통신이 필요한 경우 비밀키의 공유와 관리가 큰 부담이 된다. 실제로 구글에 “one-time pad”를 검색하면, 간첩들이 호두 껍데기 속에 숨겼을 만큼 작은 종이조각에 빼곡하게 적힌 난수(비밀키)의 사진을 볼 수 있다. 이는 원타임패드가 완벽한 보안을 제공하지만 현실적으로 키 관리가 어렵다는 점을 단적으로 보여준다.

비밀키를 재활용하면 되지 않느냐는 의문이 들 수도 있지만, 원타임패드의 안전성은 비밀키를 단 한 번만 사용할 때만 성립한다. 원타임패드에서 “원타임^One-time”이 의미하는 바가 바로 이것이다. 이는 [그림 4]에서 확인할 수 있다. 실제로 제2차 세계대전 당시 소련은 미국 내 간첩들과의 통신에 원타임패드를 사용했는데, 간혹 비밀키를 재활용하는 바람에 미국이 일부 암호문을 해독할 수 있었다. 

 
정보이론적 안전성의 한계

그럼 자연스러운 다음 목표는 원타임패드보다 더 효율적이면서도 정보이론적으로 안전한 암호화 방식을 설계하는 것일 것이다. 하지만 애석하게도, 다음의 명제가 성립함을 어렵지 않게 증명할 수 있다. 

“키공간 \(\mathcal{K}\)와 메시지공간 \(\mathcal{M}\)을 가지는 암호화 방식이 정보이론적으로 안전하다면, \(|\mathcal{K}| \ge |\mathcal{M}|\)이 성립한다.”

즉, 정보이론적 안전성을 목표한다면, 키의 가짓수는 결코 메시지의 가짓수보다 작을 수 없으며, 따라서 원타임패드보다 본질적으로 더 효율적인 암호화 방식은 존재하지 않는다는 결론에 이르게 된다. 

섀넌을 현대암호학의 기점으로 보는 이들은 암호가 처음으로 수학적 대상이 된 순간을 기준으로 삼았을 것이다. 섀넌에 이르러서야 암호가 비로소 “정의-정리-증명”의 대상이 되었다는 점에서 이는 분명 기념비적인 성취이다. 그러나 섀넌의 정의는 너무도 엄격하여 극도로 비효율적인 원타임패드만을 포착한다는 점에서 한계가 뚜렷하다. 만약 이전 글에 등장했던 에드거 앨런 포가 살아서 섀넌의 결과를 접했다면, 대수롭지 않다는 듯 자신의 말을 아주 살짝 수정했을지도 모른다.

“인간 지성이 고안한 모든 *쓸만한* 암호는 결국 인간 지성에 의해 해독될 수밖에 없다.”

그리고 그 후

그 이후에는 어떻게 됐을까? 모두가 비효율적이지만 완벽한 안전성을 보장하는 원타임패드를 사용했을까? 아니면 효율적이면서도 완벽하게 안전한 암호는 존재할 수 없다는 사실에 좌절하고 암호화를 포기했을까? 하지만 암호학은 본래부터 실용 학문이다. 현실적인 이유로 타협할 수밖에 없었고, 정보이론적 안전성의 개념은 분명 암호에 대한 시야를 넓히는 데에 기여했지만, 당시 암호 설계의 방향성을 직접적으로 바꾸지는 못했다. 

섀넌 역시 이를 충분히 예상하였다. 섀넌의 논문은 세 개의 장으로 구성되어 있는데, 1장은 암호화 방식을 이해하는 전반적인 틀을 제공하며, 2장은 정보이론적 안전성을 본격적으로 다룬다. 이어서 3장에서는 “실용적인 안전성^{Practical Secrecy}”에 대해 논의한다. 즉 정보이론적 안전성을 달성하지는 못하지만 현실에서 사용할 수 있을 만한 암호를 설계할 때 고려해야 할 요소들을 탐구한다. 이 과정에서 후대에 지대한 영향을 미칠 중요한 단서들을 남겼지만, 섀넌 본인도 논문에서 인정했듯이³ 그 자체로는 엄밀함과 견고함이 부족했다. 

그렇다면 섀넌이 말하는 “실용적인 안전성”에 이론적 토대를 마련할 수는 없을까? 특히 정보이론적으로 안전한 암호, 즉 해독이 “불가능한” 암호의 정의가 너무 엄격한 것이 문제라면, 해독이 “어려운” 암호를 고려해 보면 어떨까? 예를 들어 해독하는 데에 100해(垓) 년이 걸리는 암호를 설계하고, 그 안전성을 수학적으로 증명할 수 있다면, 비록 해독이 불가능한 것은 아닐지라도 실용적으로는 충분하지 않을까?

이를 위해서는 새로운 안전성의 정의를 기술할 수학적 언어와 이론적 틀이 필요하다. 하지만 섀넌이 활발히 활동하던 당시에는 “어렵다”는 개념을 정량화할 수 있는 수학적 언어가 아직 충분히 발전하지 않았다. 컴퓨터 기술의 고도화, 계산복잡도 이론^{Complexity Theory}의 성숙, 그리고 산업에서 새로운 기능의 암호를 요구하는 환경이 모두 갖춰질 때까지는 섀넌의 논문 이후 약 30년의 세월이 더 필요했다. 

다음 글에서는 1970년대의 시대적 배경과 함께, 디피^{Whitfield Diffie; 1944~}와 헬만^{Martin Hellman; 1945~}이 제시한 “암호학의 새로운 방향^{New Directions in Cryptography”}에 대해 알아보도록 하자.