[10월의 퍼즐 해설] 아이스크림 케이크 일도양단

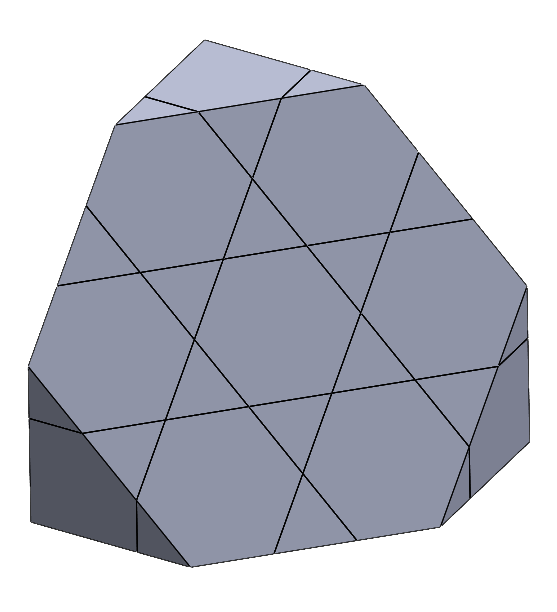
아이스크림 케이크의 초기 상태는 27개의 조각으로 이루어져 있다. 각 조각은 정육면체, 즉 볼록다면체이기 때문에 평면으로 자르면 최대 2개의 조각으로 나누어진다. 따라서 절단면이 27개의 조각들 중 최대 몇 개의 조각을 지나게 할 수 있는지를 구하면 케이크가 최종적으로 몇 개의 조각으로 나누어질지도 알 수 있다. 예를 들어 만약 절단면이 27개의 조각들 중 10개를 지난다면, 케이크는 최종적으로 27 + 10 = 37조각으로 나누어지게 될 것이다.

여기서 하나, 조각 수를 최대화하기 위하여 절단면은 완전한 수평이 아니라고 가정할 수 있다. 완전히 수평으로 자르면 절단면은 9개의 조각을 지나므로 최종적인 조각 수는 27+9=36개가 될 것이다. 그러나 그것보다는 조각 수를 많게 하는 방법이 있음은 자명하다.

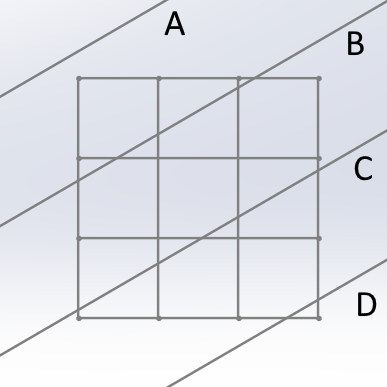
이제 다음과 같이 케이크를 위에서 내려다본 그림 위에 직선 4개를 등간격으로 그려 보자. 각각의 직선은 절단면이 [케이크의 윗면을 포함하는 평면], [케이크 2층과 3층 사이의 면을 포함하는 평면], [케이크 1층과 2층 사이의 면을 포함하는 평면], [바닥면]과 교차하는 직선을 의미한다. 절단면이 완전한 수평이 아니라고 가정했으므로 4개의 직선 모두 반드시 존재한다. 이 4개의 직선을 순서대로 A, B, C, D라고 하자.

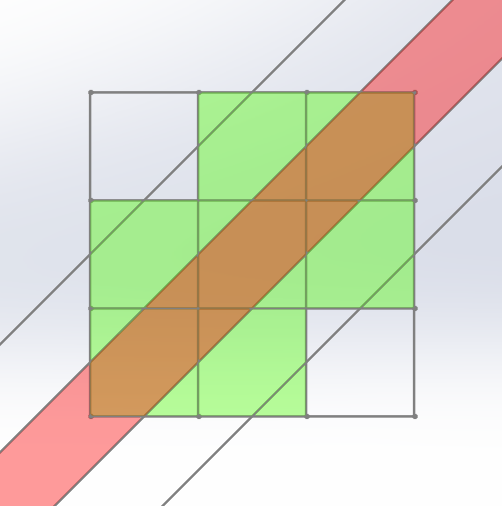
그러면 [A와 B 사이의 영역]이 케이크의 3층을 절단하는 절단면이 되고, [B와 C 사이의 영역]이 케이크의 2층을 절단하는 절단면이 되고, [C와 D 사이의 영역]이 케이크의 1층을 절단하는 절단면이 된다. 예를 들어, 위 그림에서는 다음 영역이 케이크의 2층을 절단하는 절단면이다.

이 영역은 다음과 같이 9개의 정사각형 중에서 8개의 정사각형을 지난다. 지나는 정사각형들을 초록색으로 칠했다.

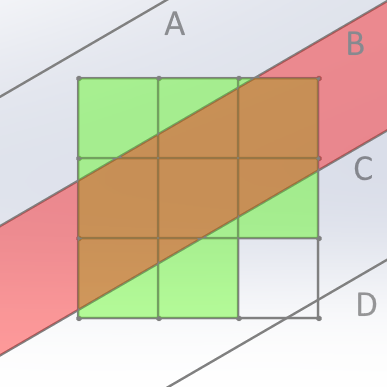즉, 위와 같이 자른다면 2층에 있는 9개의 조각들 중 8개의 조각이 절단면에 의해서 둘로 나뉜다는 뜻이다.

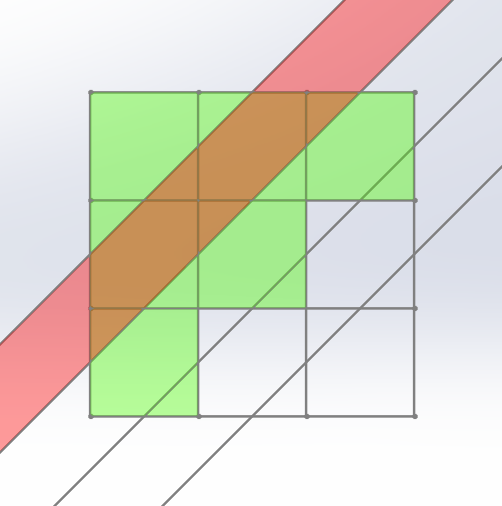
이제 문제를 이해하기 쉽게 재정의할 수 있다. [A와 B 사이의 영역]이 만나는 정사각형의 개수 + [B와 C 사이의 영역]이 만나는 정사각형의 개수 + [C와 D 사이의 영역]이 만나는 정사각형의 개수를 어떻게 하면 최대화할 수 있을까? 구해진 답에 원래 조각 개수인 27을 더하면 최종적인 조각 개수가 된다. 조금씩 다른 여러 가지 정답이 존재하지만, 가장 예쁜 모양의 정답을 소개하자면 다음과 같다.

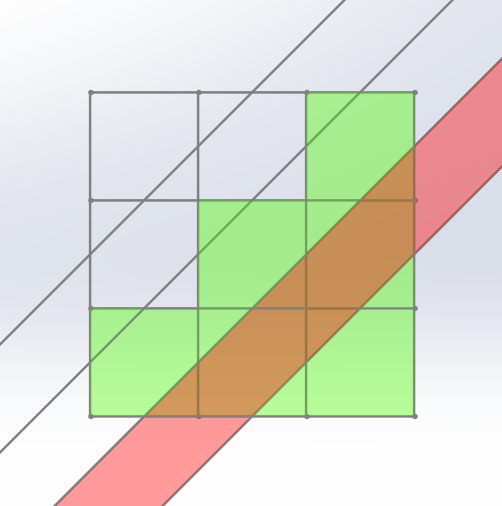이 절단면은 3층에서 6개의 조각과 만나고, 2층에서 7개의 조각과 만나고, 1층에서 6개의 조각과 만난다. 즉 절단에 의해 19개의 조각이 추가로 생겨, 케이크는 최종적으로 27 + 19 = 46개의 조각으로 나누어진다.

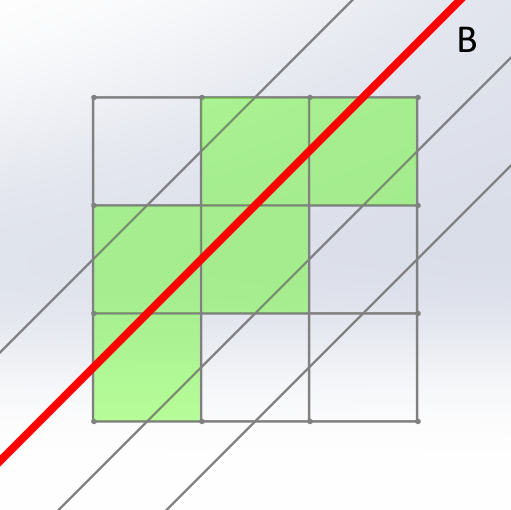
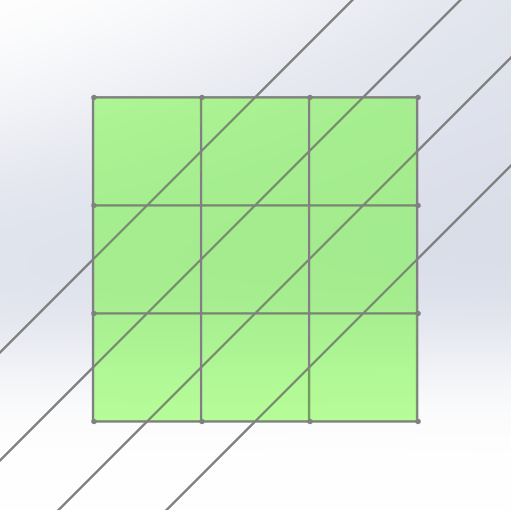
위 그림과 같이 19개의 조각을 절단하는 것이 최선이라는 것은 다음과 같이 보일 수 있다. 3층의 초록색 정사각형 중 직선 B와 만나지 않는 정사각형을 2층으로 옮기고, 1층의 초록색 정사각형 중 직선 C와 만나지 않는 정사각형을 2층으로 옮기면 다음과 같은 그림이 된다.

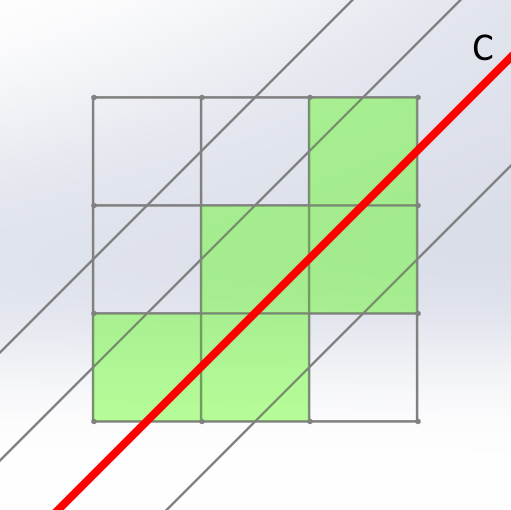이때 3층에 남는 초록색 정사각형은 직선 B가 만나는 정사각형이 되고, 1층에 남는 초록색 정사각형은 직선 C가 만나는 정사각형이 된다.

초록색 정사각형의 개수를 최대화하기 위해서는 2층에 있는 정사각형들이 최대한 많이 초록색으로 칠해지고, 직선 B와 C는 최대한 많은 정사각형을 지나야 한다. 그런데 이 방법은 2층에 있는 정사각형을 9개 전부 초록색으로 칠했고, 직선 B와 C는 5개의 정사각형을 지났으므로 (가장 많이 지나는 경우가 5개임은 쉽게 알 수 있다) 초록색 정사각형의 개수를 최대화하는 방법이다.

위 방법대로 실제로 나누어진 모습은 다음과 같다.

단면은 이렇게 생겼다. 절단면이 19개의 조각을 지나는 것을 확인할 수 있다.

답) 대각선으로 많이 눕혀서 잘라야 27+19 = 46 (근데 너무 작은 조각을 먹는 친구가..)