프랙털 기하학의 선도자인 만델브로(Benoit B. Mandelbrot)는 확대, 축소의 각 배율마다 자기 반복성 또는 유사성을 가지는 기하학적인 형태를 프랙털이라 명명하였다. 프랙털 구조는 자연계에서 흔히 볼 수 있는데, 가장 대표적인 예로 우리 몸의 허파를 들 수 있다. 허파 속의 기관지는 프랙털의 라틴어 어원처럼 쪼개지고 갈라지고 나뉘어서 호흡세기관지가 된다. 그 끝에는 허파꽈리가 붙어있는데, 이곳에서 산소와 이산화탄소의 교환이 이루어진다. 만약 포유류의 허파꽈리가 프랙털 구조를 가지지 않고 매끈한 2차원 표면이었다면, 산소와 이산화탄소의 교환이 충분히 이루어지지 않아 생존을 유지하기 어려웠을 것이다. 만델브로는 자연계에서 흔히 볼 수 있는 거친 형태인 프랙털을 다음과 같은 일상의 언어로 표현하였다. “구름은 구형이 아니고, 산은 원뿔이 아니며, 해안선은 원이 아니고, 나무껍질은 매끈하지 않다. 번개는 직선처럼 치지 않는다.”
프랙털 개념은 라이프니츠(Gottfried Leibniz)가 점화적 자기 유사성을 고안한 17세기로 거슬러 올라갈 수 있지만, 라이프니츠는 이러한 자기 유사성을 가진 기하학적인 대상은 직선밖에 없다고 주장하는 오류를 범하였다. 비자명한 프랙털의 예는 19세기 말에 이르러서야 등장하게 되는데, 바이어슈트라스(Karl Weierstrass)는 푸리에 급수를 이용하여 모든 점에서 연속이지만, 모든 점에서 미분이 가능하지 않은 함수를 고안하였다. 확률 프랙털의 대표적인 예인 일차원 브라운 운동은 바이어슈트라스 함수처럼 (확률 \(1\)로) 모든 점에서 연속이지만, 모든 점에서 미분이 가능하지 않다. 바이어슈트라스의 제자였던 칸토르(Georg Cantor)는 스승의 강연에서 영감을 얻어 칸토르 집합을 고안하였다.
20세기 초에 이르러 민코프스키(Hermann Minkowski)와 하우스도르프(Felix Hausdorff)는 차원의 개념을 자연수가 아닌 실수로 확장하였다. 민코프스키 차원(상자 세기 차원)은 계산이 용이하고, 수치해석적인 계산이 가능하여 실용적이기는 하지만, 측도론과 부합하지 않는 단점이 있다. 예를 들어, 칸토르 집합은 길이가 \({({\frac13)}^n}\) 인 선분 \({2^n}\) 개로 덮을 수 있고, 민코프스키 차원은 하우스도르프 차원과 같이 \({\frac{\log2}{\log3}}\) 이 된다. 반면, 유리수 집합은 실수 집합에서 조밀하므로, 민코프스키 차원은 \(1\)이지만, 셀수있는 집합이므로 하우스도르프 차원은 \(0\)이 된다. 만델브로는 바이어슈트라스 함수 그래프의 하우스도르프 차원을 예측하였는데, 이의 증명은 아직까지 미해결로 남아 있다. 반면, 일차원 브라운 운동의 그래프는 확률 \(1\)로 하우스도르프 차원 \(\frac { 3 }{ 2 }\)을 가짐이 잘 알려져 있다.
사진에 찍힌 구름은 평면 위의 브라운 운동으로 이의 바깥 경계는 확률 프랙털 구조를 가지고 있다. 만델브로는 이 브라운 경계의 하우스도르프 차원이 확률 \(1\)로 \(\frac { 4 }{ 3 }\) 임을 예측하였다. 이후 수치해석과 수리물리의 등각장론(conformal field theory)에서 만델브로 예측을 뒷받침하는 결과들이 있었는데, 롤러(Gregory Lawler), 슈람(Oded Schramm), 베르너(Wendelin Werner)는 슈람-뢰브너 전개(Schramm-Loewner evolution, SLE)를 이용하여 20세기 말에 만델브로 예측을 증명했다. 이 결과로 베르너는 2006년 필즈상을 수상하였다. 안타깝게도 슈람은 2008년에 등반사고로 목숨을 잃게 되는데, 뉴욕 타임즈 부고에 다음 내용이 실렸다. “만약 슈람 박사가 3주하고도 하루 늦게 태어났더라면, 2002년 필즈상을 받았을 것이 거의 확실했다.” (필즈상은 4년마다 개최하는 세계 수학자 대회에서 40세 미만의 젊은 수학자에게 수여된다.)
슈람이 평면 임계 격자 모형의 경계 곡선 극한의 유일한 후보로 슈람-뢰브너 전개를 도입한 이래, 슈람-뢰브너 전개는 임계 삼투 모형과 이징 모형을 비롯한 여러 모형의 경계 곡선의 극한의 존재성 및 등각불변성(각을 보존하는 복소함수에 의해 변하지 않은 성질)을 증명하는데 주요한 도구로 이용되어왔다. 슈람이 슈람-뢰브너 전개를 처음 도입하였을 때, 확률 뢰브너 전개(Stochastic Loewner evolution)라고 명명하였으나, 동료들이 그의 업적을 기려 그의 성을 따라 부르게 되었다. 슈람이 그와 같이 될 것이라고 예측하여, random Loewner evolution으로 명명하지 않고 그의 성과 같이 시작하는 Stochastic Loewner evolution이라고 명명하지 않았을까하는 의구심을 혹자가 농담으로 슈람에게 건네는 모습을 목격한 적이 있다.
필자가 대학원생이었을 때, 슈람이 예일대학교 수학과 Hahn lecture series에서 강연을 한 적이 있었다. 그가 SLE를 고안했을 때, 확률론 배경지식이 깊지 않았음을 고백했는데, 신선한 충격으로 다가왔었다. SLE 이론에 확률론의 이토 공식이 필요함을 알았을 때, 익숙하지 않은 분야를 공부해야하는 부담감을 솔직히 이야기하였다(슈람은 서스톤(William Thurston)의 학생이었다). 그렇지만 그는 이토 공식이 테일러 전개의 환상적인 버전임을 자각하는데 그다지 오래 걸리지 않았다고 덧붙였다.
또한 혹자들은 슈람이 뢰브너 전개의 확률 버전을 생각하게 된 계기가 그의 동료 로드(Steffan Rohde)의 한 강연이었을 것이라고 추측한다. 뢰브너 전개는 뢰브너(Charles Loewner)가 비버바흐 추측(Bieberbach conjecture)에 도전하기 위해 도입하였으며, 실제로 이를 이용하여, 그는 세 번째 계수에 관한 부등식을 얻었다. 비버바흐는 단위원에서 정의된 \(1\)-\(1\) 정칙함수의 테일러 \(0\)번째 계수는 \(0\)이고 \(1\)번째 계수는 \(1\)로 정규화 되었을 때, \(n\)번째 계수의 절댓값이 \(n\)보다 작거나 같다고 추측하였다. 후에, 이 추측은 일반적인 경우에 성립함을 드 브랑주(Louis de Branges)가 증명하였다.
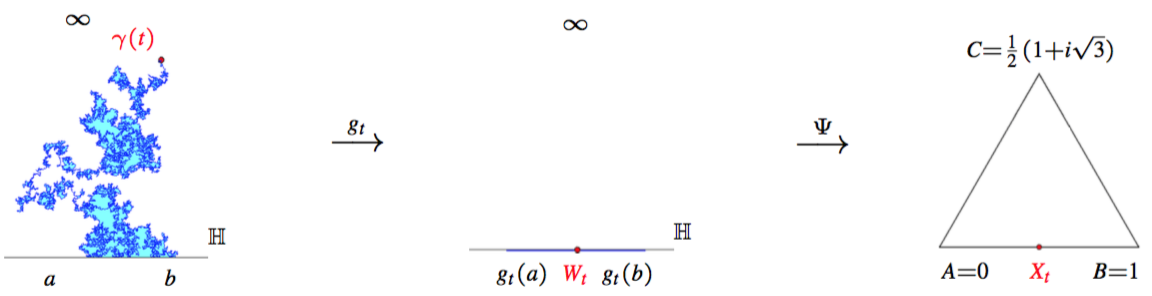
평면 임계 격자 모형의 경계 곡선의 극한이 등각불변임이 예측되어 왔는데, 슈람은 또한 극한 확률곡선이 영역 마르코프 성질을 만족하게 된다는 사실에 주목하였다. 확률 곡선이 단순 곡선인 경우에, 단순연결 영역 \(D\)의 경계점 \(p\)에서 출발하여 다른 경계점 \(q\)에 도달할 곡선이 현재 \(r\)에서 멈추어 있을 때(그림 2의 왼쪽 그림 참조), 과거의 분포를 조건으로 하여 확률 곡선의 미래의 조건부 분포(그림 2의 가운데 그림 참조)가 기존의 단순연결 영역에서 과거 자취를 제외한 새로운 단순연결 영역의 경계점 \(r\)에서 출발하여 경계점 \(q\)에 도달할 확률 곡선의 분포(그림 2의 오른쪽 그림 참조)가 같을 때 확률 곡선이 영역 마르코프 성질을 만족한다고 정의한다. 확률곡선이 등각불변이라 함은 단순연결 영역과 경계점 (\(D\),\(p\),\(q\)), (\(D’\),\(p’\),\(q’\)) 사이의 리만 함수 \(f\)에 대하여 \(p\)에서 출발하여 \(q\)에 도달하는 \(D\)내의 확률 곡선의 \(f\)에 의한 상과 \(p’\)에서 출발하여 \(q’\)에 도달하는 \(D’\) 내의 확률 곡선이 같은 분포를 갖게 됨을 뜻한다.

\({ { \partial }_{ t }g }_{ t }\left( z \right) =\frac { 2 }{ { g }_{ t }\left( z \right) -{ W }_{ t } }\), \({ W }_{ 0 }=0,\quad { g }_{ 0 }\left( z \right) =z\)
운동함수 \({ W }_{ t }\)는 \({ g }_{ t }\)에 의한 시각 \(t\)에서 곡선 위치의 상이 된다. 따라서, 곡선의 모든 정보가 실수 축을 따라 움직이는 운동함수에 저장되는데, 만약 곡선이 영역 마르코프 성질과 허수 축에 관해 대칭성을 만족하게 되면, 운동함수는 일차원 브라운 운동이 된다. 브라운 운동의 속력이 \(k\)일 때, 확률 곡선을 SLE(\(k\))라 부른다.
통계물리의 많은 격자 모형들이 SLE(\(k\))에 대응된다고 증명 또는 예측되어 왔다. 예를 들어 롤러, 슈람과 베르너는 닫힌곡선 지우며 마구잡이 걷기(loop erased random walk), 균등 형성 나무(uniform spanning tree, UST)가 각각 SLE(\(2\)), SLE(\(8\))로 수렴함을 증명하였다. 슈람과 쉐필드(Scott Sheffield)는 조화 탐험(harmonic explorer), 가우스 자유장의 등고선이 SLE(\(4\))로 수렴함을 증명하였다. 스미르노프(Stanislav Smirnov)는 임계 삼투 모형(critical site percolation)과 임계 이징 모형(Ising model)의 경계 곡선 극한의 존재성과 등각불변성을 슈람-뢰브너 전개를 이용하여 증명한 공로로 2010년 필즈상을 수상하였다. 스미르노프는 임계 삼투 모형이 SLE(\(6\)), 이징 모형이 SLE(\(3\)), FK 이징 모형이 SLE(\(\frac { 16 }{ 3 }\) )로 수렴함을 증명하였다.

슈람과 쉐필드는 격자 위의 이산 가우스 자유장의 경계 조건을 적절히 부여한 후 등고선들 중, 경계점을 잇는 곡선이 SLE(\(4\))로 수렴함을 증명하였다. 이에 앞서 이 격자 모형의 단순 명료한 대체 모형으로 조화 탐험을 도입하고 이 모형이 SLE(\(4\))로 수렴함을 밝혔다. 단순 연결 영역 내 평면 벌집 격자의 조화 탐험은 유무색의 육각형을 경계짓는 확률 곡선이다. 초기 조건으로 왼쪽 경계는 유색으로, 오른쪽 경계는 무색으로 (비확률적으로) 주어진다. 각 스텝에서 조화 탐험은 유무색이 정해지지 않은 육각형에서 끝나는데, 이 육각형의 색은 이 중심에서 출발하여 벌집 격자의 쌍대 격자를 따라 움직이는 마구잡이 걷기(random walk)가 처음으로 만나는 유무색 육각형의 색으로 결정된다. 결정된 색에 따라 조화 탐험은 다음 스텝에서 좌회전 또는 우회전하게 된다.
이제 조화 탐험이 왜 SLE(\(4\))에 대응하는지, 즉 조화탐험에서 운동함수를 어떻게 인지할 수 있는지 간략한 설명을 덧붙인다. 복소 상반평면 상의 조화 측도 (1/π) arg \(z\)는 \(z\)에서 출발한 2차원 브라운 운동이 상반평면을 벗어날 때, 음의 실수 축을 칠 확률을 나타낸다. 등각불변성에 의해 SLE 영역의 조화 측도 (1/π) arg \({ Z }_{ t }\left( { Z }_{ t }=g_{ t }\left( z \right) -{ W }_{ t } \right)\)는 \(z\)에서 출발한 2차원 브라운 운동이 SLE 영역을 벗어날 때, 음의 실수 축 또는 SLE 곡선의 왼쪽 부분을 칠 확률을 의미한다. 만약 \(k\)가 \(4\)이면, 이토 공식과 뢰브너 방정식에 의해 확률과정 (1/π) arg \({ Z }_{ t }\)는 마팅게일이 된다. 확률과정이 마팅게일이라 함은, 주식의 미래 가격 기댓값이 현재 가격과 동일하듯이, 확률과정이 현재까지의 정보를 조건으로 할 때, 미래의 조건부 기댓값이 현재 값과 같다는 것을 뜻한다. 현재 시각 \(t\)에서, 마팅게일 (1/π) arg \({ Z }_{ t }\)는 현재까지의 정보를 조건으로 점 \(z\)가 SLE(\(4\)) 곡선의 왼쪽에 위치할 조건부 확률을 나타낸다. 조화 탐험의 정의에 따르면, 조화 탐험도 이와 비슷한 성질을 가지고 있다. 일반적으로, 이와 같은 마팅게일 관측이 SLE 분포를 유일하게 결정한다. 격자 모형의 경계 곡선의 수렴성을 증명하기 위해 롤러-슈람-베르너가 고안한 주된 도구 중 하나가 마팅게일 관측이다.
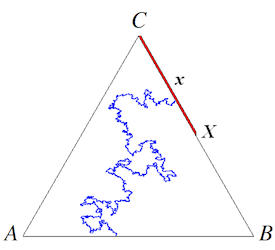
정육각형 삼투 모형은 정육각형 격자구조를 가지는 벌집의 각 격자가 열려 있을 사건이 확률 \(p\)로 (닫혀 있을 사건이 \(1-p\)로) 독립적으로 일어나는 모형이다. \(p\)가 작을수록 열려 있는 격자들의 연결 영역은 줄어들고 \(p\)가 클수록 늘어난다. 이 모형은 임계확률 \(p_{ c }=\frac { 1 }{ 2 }\)에서 상전이가 일어난다. 임계확률 전후로 복소평면에서 무한 열린 연결 영역의 존재성 여부가 갈린다. 직사각형 영역에서 정의된 임계 벌집 삼투 모형에서 직사각형 윗변에 물을 부으면 물이 열려 있는 격자를 따라 밑변에 도달할 사건의 확률은 격자의 너비가 \(0\)으로 갈 때 극한을 가지는데, 이 극한값을 물리학자 카디(John Cardy)는 등각장론을 이용하여 직사각형 높이와 너비의 비로 예측하였다. 이 극한값을 카디의 공식이라 부른다. 또한, 이 극한값이 등각불변임이 예측되었는데, 스미르노프가 이를 증명하였다. 카디의 공식은 직사각형 내부를 이와 등각동형인 정삼각형 내부로 대체하면 매우 간단해지는데(등각성질은 경계로 확장되지 않는다), 이 버전은 2006년도 아벨상 수상자인 칼레슨(Lennart Carleson)이 처음으로 인지하였다. 한 변의 길이가 \(1\)인 정삼각형 \(ABC\)의 변 \(BC\) 위의 점 \(X\)가 점 \(C\)에 이르는 거리가 \(x\)일 때, 변 \(CX\)와 변 \(AB\)를 잇는 열린 횡단길이 존재할 확률의 극한값이 \(x\)가 된다.
단순연결 영역과 경계점 (\(D\),\(p\),\(q\))은 \(p\)를 기준으로 영역의 경계를 좌우로 나눈다. 이제 (\(D\),\(p\),\(q\))을 정육각형 격자구조로 근사한 후, 비확률적으로 왼쪽 경계 격자는 닫고 오른쪽 경계 격자는 열고, 내부 격자는 임계확률 \(\frac { 1 }{ 2 }\)로 독립적으로 열면, \(p\)근처에서 출발하여 \(q\) 근처로 끝나는 열린 격자와 닫힌 격자를 분리하는 경계 곡선을 얻는다. 격자의 크기가 \(0\)으로 갈 때, 이 경계 곡선이 수렴하고, 그 극한 확률 곡선이 등각불변이며, SLE(6)로 수렴함을 카디 공식의 칼레슨 버전을 이용하여 스미르노프가 증명하였다.
이제 스미르노프가 뢰브너 전개의 운동함수를 인지한 아이디어를 소개하겠다. 주어진 음의 실수 \(a\)와 양의 실수 \(b\)에 대하여, 상반평면에서 정의된 임계 삼투 모형의 경계 곡선의 극한이 구간 (\(b\),\(∞\))를 치기 전에 구간 (\(-∞\),\(a\))를 칠 사건 \(E\)를 고려하자. 이 확률 곡선에 대응하는 뢰브너 전개 \({ g }_{ t }\)에 의한 \(a\), \(b\), \(∞\)의 상 \({ g }_{ t }\left( a \right)\), \({ g }_{ t }\left( a \right)\), \(∞\)을 정삼각형 \(ABC\)의 세 꼭지점으로 보내는 리만함수는 운동함수 \({ W }_{ t }\)를 선분 \(AB\) 위의 한 점 \({ X }_{ t }\)로 보낸다. 점 \(A\)를 \(0\), 점 \(B\)를 \(1\)로 놓으면 \({ X }_{ t }\) 는 극한 경계 곡선의 현재 시각 \(t\)까지의 정보를 조건으로 사건 \(E\)가 일어날 조건부 확률을 나타내고, 따라서 \({ X }_{ t }\)는 마팅게일이 된다. 이토 공식과 뢰브너 방정식에 의해 운동함수는 속력이 \(6\)인 일차원 브라운 운동이 된다.
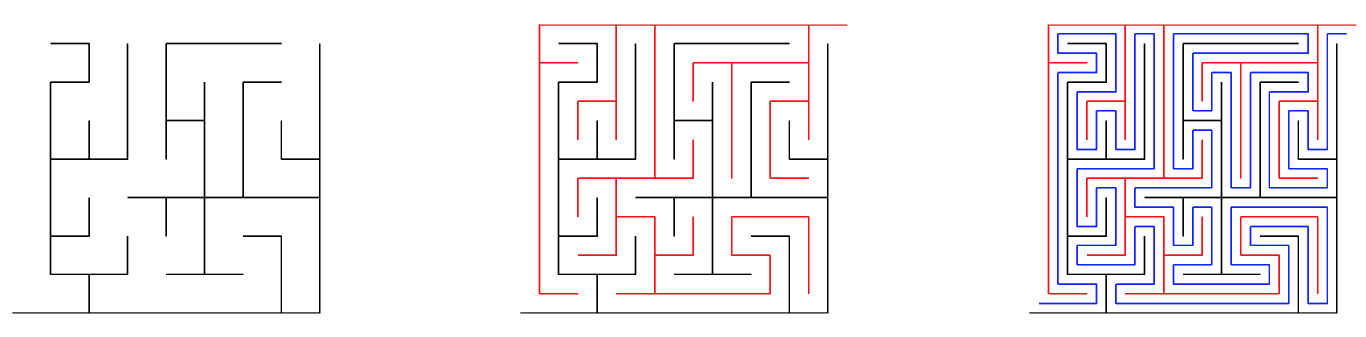
다음으로 균등 형성 나무(uniform spanning tree, UST)의 마팅게일 관측을 간략히 기술해 보고자 한다. 균등 형성 나무는 바둑판 모양의 격자에서 정의된 랜덤 그래프로, 바둑판 정사각형의 각 꼭짓점을 모두 지난다는 의미에서 ‘형성’이고, 루프가 없는 ‘나무’ 구조를 가지고 있으며, 이러한 형성 나무가 발생할 확률이 균등하게 주어진다. 바둑판 위를 동서남북으로 균등하게 독립적으로 움직이다가 꼭짓점을 처음 방문할 때 전 꼭짓점 사이에 나무를 놓으면 UST를 얻게 되는데 이를 윌슨 알고리듬(Wilson’s algorithm)이라고 부른다. 그림 9의 왼쪽 그림에 있는 wired UST와 중간 그림에 있는 이의 쌍대 그래프로 벽을 세우면 미로처럼 보이지만, 아주 쉽게 길을 찾을 수 있다. 남서쪽 입구에서 출발하면, 전방에 검은 벽을 만나면 좌회전, 붉은 벽을 만나면 우회전하여 북동쪽 출구에 도달할 수 있다. 이 탈출 경로를 그림 9의 오른쪽 그림처럼 파란색으로 그리면, 페아노 곡선을 얻게 된다.
롤러, 슈람과 베르너는 이 페아노 곡선이 격자 크기가 \(0\)으로 가면, 평면을 채우는 SLE(\(8\)) 곡선으로 수렴함을 증명하였다. SLE(\(8\)) 마팅게일 관측
\({M_t(z,x):=\frac1\pi arg\frac{1-\sqrt{z/x}}{1+\sqrt{z/x}},\quad x\in(0,\infty)}\)
은 상반평면 위의 점 z에서 출발하고 음의 실수 축을 만나면 반사하는 브라운 운동이 구간 \({\partial_1=(0,x)}\)을 치기 전에, 구간 \({\partial_2=(x,\infty)}\)을 칠 확률을 나타낸다. 이에 대응하는 이산 마팅게일 관측은 경계 \({\partial_1^\delta}\) 를 치지 않고 점 \(z_\delta\)과 경계 \(\partial_2^\delta\)를 잇는 곡선이 wired tree 안에 존재할 확률이다. 여기서 \(z_\delta\), \({\partial_1^\delta}\), \({\partial_2^\delta}\)는 격자 크기가 \(\delta \)일 때 \(z,{ \partial }_{ 1 },{ \partial }_{ 2 }\)의 이산 격자 근사이다.
카디 공식의 예에서 보듯이, 등각장론은 통계물리의 이차원 격자 모형의 등각불변인 임계 클러스터에 관한 정확한 결과를 유도하는데 유용하게 활용되었다, 등각장론은 수학에서 비라소로 표현론과 같은 대수학의 발전에 큰 영감을 제공해왔다. 통계물리의 “정확한” 결과의 “엄밀한” 수학적 증명이 최근 20년간 복소해석학과 확률론 관점에서 진행되어 왔는데, 그 주요한 도구가 슈람-뢰브너 전개이다. 이러한 증명의 중요한 부분은 마팅게일 관측을 찾는 일인데, 알려진 대부분의 마팅게일 관측들은 등각장론의 상관관계함수로 표현된다. 필자는 이러한 슈람-뢰브너 마팅게일 관측을 해석학적 등각장론을 이용하여 체계적으로 연구하고 있다. 또한 스트레스 에너지 텐서 개념을 상관관계함수에 작용하는 리 미분 작용소에 대응하는 장의 개념으로 설명하는 등 등각장론을 해석학적으로 엄밀히 정립하고 있다. 다중 연결 영역, 다중 슈람-뢰브너 전개, 일반적인 리만 곡면 등을 포함한 다양한 등각 형태의 등각장론을 복소해석학과 확률론 관점에서 정립하고, 분류할 예정이다.