2016년 3월 서울에서, 바둑 기보를 딥러닝Deep Learning 기술로 공부한 딥마인드 Deepmind의 알파고AlphaGo가 이세돌 9단을 이기며 온 국민에게 충격을 준 이후 벌써 3년이 흘렀다. 그 후 기보를 공부하지 않은 알파고 제로AlphaGo Zero가 개발되었고 인간과의 대결이 더이상 무의미한 경지에 이른 후 은퇴를 하였다.1 이를 비롯해 우리는 4차 산업혁명 시대에서 하루가 다르게 새로운 수많은 인공지능 기술들을 경험하고 있다.
대중의 입장에서는 2016년 이후 알파고AlphaGo를 비롯한 수많은 인공지능 기술들이 혁명처럼 한순간 다가온 것 같지만, 사실 이 모든 것들은 연구자들이 오랜 기간 발전시켜 온 여러 이론과 기술들을 바탕으로 이루어졌다. 이 글은 그 중 최적화Optimization 이론에 대해 이야기해보고자 한다.
최적화라는 단어는 모두가 익숙할 것이다. 이는 바로 우리가 자연스레 일상 속에서 최적화의 과정들을 거치기 때문이다. 집에서 학교 혹은 직장까지 최단 경로를 고려할 때, 하루에 주어진 일을 해결할 순서를 정할 때, 여행 계획을 짤 때, 우리는 시간과 비용 등을 고려한 최적화의 과정을 거친다. 잠시만 곰곰이 생각해보면, 이 모든 최적화 과정을 수리적으로 나타낼 수 있다는 것을 알 수 있을 것이다(아니라면 이 글을 통해 차차 배우게 될 것이다). 그리고 곧 설명하겠지만 딥러닝을 비롯한 기계학습Machine Learning 역시 최적화 과정을 거친다. 이외에도 최적화는 전자공학, 컴퓨터공학, 산업공학, 경제학 등의 다양한 곳에서 오래전부터 쓰이고 있다.
1. 수리최적화Mathematical Optimization
수리최적화는 계산수학의 한 갈래로 주어진 후보들 \(x\in S\) 중에서 목적 함수Objective Function \(f(x)\)를 최소화 (혹은 최대화)하는 최적해Optimum를 찾는 것을 일컫는다. 이를 수학적으로 간단히 표현하면 아래와 같다.
\(\begin{align*}
minimize_{x\in S} f(x)
\quad\left(\text{or}\quad maximize_{x\in S} f(x)\right)
\end{align*}\)
아래의 조건을 만족하는 \(x_\star\in S\)가 최적해이며, 전역 최소해Global Minimum라고도 부른다.
\(\begin{align*}
f(x_\star) \le f(x) \text{ for all } x\in S
\end{align*}\)
전역 최소해를 찾는 것이 일반적으로 어려우므로 (NP-hard하므로), 지역 최소해를 찾는 것만으로도 때때로 충분히 의미 있게 생각된다. 지역 최소해Local Minimum는 아래 조건을 만족하는 \(\delta>0\)가 존재하는 \(\bar{x}_\star\in S\)를 일컫는다.
\(\begin{align*}
f(\bar{x}_\star) \le f(x) \text{ for all } x\in S \text{ and } ||x – \bar{x}_\star|| \le \delta
\end{align*}\)
참고로 딥러닝을 비롯한 기계학습 분야에서 지역 최소해가 아닌 전역 최소해를 찾는 방법에 대해 최근 많은 연구가 이루어지고 있다. 이는 좋은 최적해를 찾는 것이 기계학습의 성능과 큰 관련이 있기 때문이다.
여행 계획을 짜는 것을 어떻게 위와 같은 수리최적화 문제로 나타낼 수 있을까? \(S\)를 가능한 모든 여행 계획의 집합으로 정하고, \(f(x)\)는 각 여행 계획에 따른 시간과 비용 등을 계산하는 목적 함수로 정하고, 여행자가 그 중 \(f(x)\)가 가장 낮은 여행 계획을 정한다고 생각하면 쉽게 이해할 수 있다. 조금 더 상세히 예를 들어보자면, 여행자가 \(S = \{x_1, x_2\}\) 두 가지 가능한 여행 계획 중에서 비용이 적게 드는 계획을 원한다면 \(f(x)\)를 비용 함수로 정했다고 볼 수 있다. 만약 \(f(x_1) = 20\)만원이고 \(f(x_2) = 15\)만원이라면 최적화 과정을 거쳐 여행자는 두 번째 계획을 선택할 것이다. 이렇게 최적화는 최적화 문제를 설정하고, 이의 최적해를 찾는 두 가지 과정을 거친다.
여기서 똑똑한(?) 사람은 의문을 가질 것이다. 여행자에 따라 절대적인 비용이 낮은 여행이 아니라, 가성비가 좋은 여행지, 선호하는 여행지, 안전한 여행지 등 여러 사항을 고려할 것이기 때문이다. 따라서 여행자에 따라 \(f(x)\)와 \(S\)가 다를 것이라는 것을 쉽게 알 수 있을 것이며, 이것을 어떻게 정하는가에 따라 최종 여행계획이 달라질 것이라는 것 역시 쉽게 이해할 수 있다. 이런 일련의 과정이 최적화와 기계학습에서 매우 중요한 부분이며 이에 대해 이야기하고자 한다.
2. 최적화와 기계학습
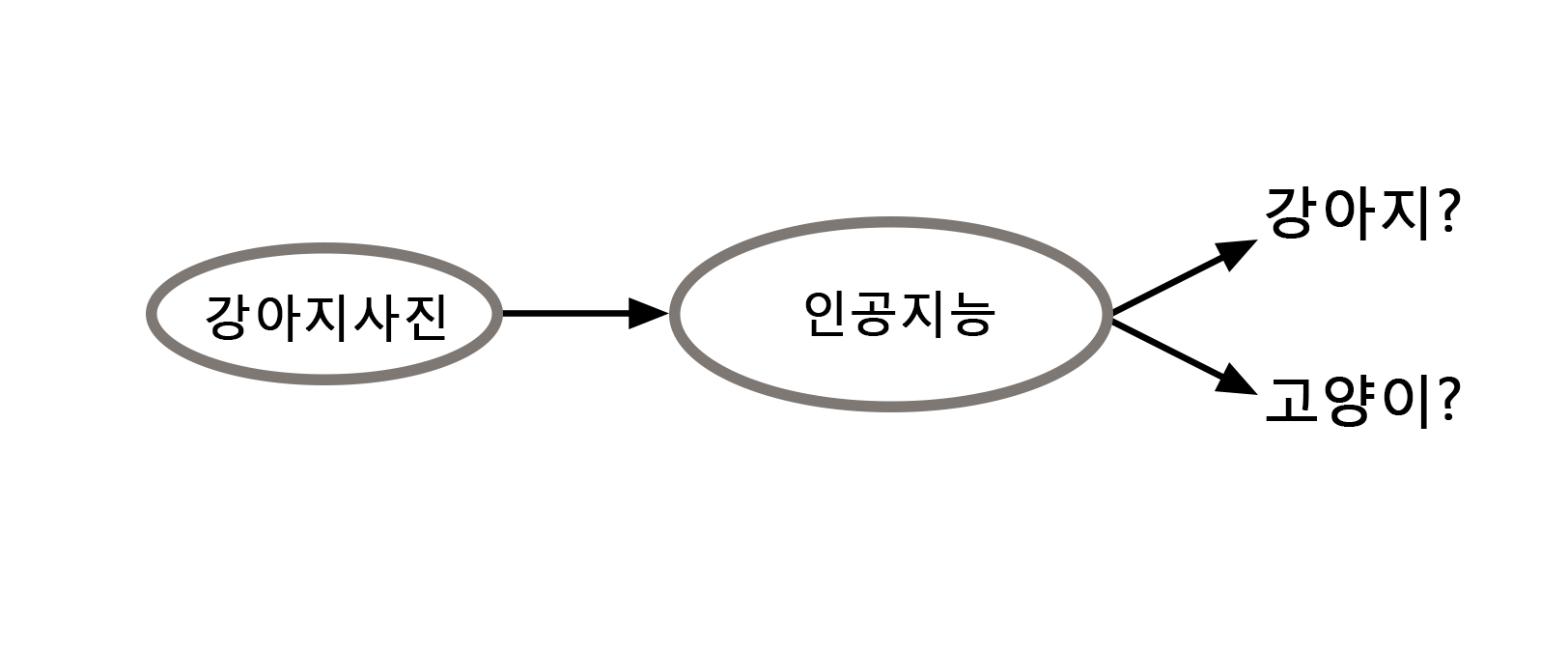
최적화 이론에서 바라봤을 때, 기계학습은 주어진 데이터 혹은 정보를 바탕으로 목적 함수 \(f(x)\)와 \(S\)를 설정하고 최적의 “인공지능”인 최적해 \(x_\star\) (혹은 \(\bar{x}_\star\))를 찾는 것이다. 기계학습을 위한 최적화를 쉽게 이해하기 위해 간단한 분류Classification 문제를 공부해보자. 우리에게 수많은 (\(N\)개의) 강아지와 고양이 사진이 주어졌을 때, 강아지와 고양이를 구분할 수 있는 인공지능 기술은 어떻게 만들어지는 걸까?
먼저 위의 문제를 수리최적화 문제로 변환하기 위해 총 \(N\)개의 사진 중 \(i\)번째 사진을 \(u_i\in\mathbb{R}^d\)라 하고2, 사진에 있는 동물에 따라 아래와 같이 \(y_i\) 값으로 \(-1\) 혹은 \(1\)을 할당하자.
\begin{align*} y_i = \begin{cases} -1, & u_i\text{가 강아지 사진이면}, \\ 1, & u_i\text{가 고양이 사진이면.} \end{cases} \end{align*}
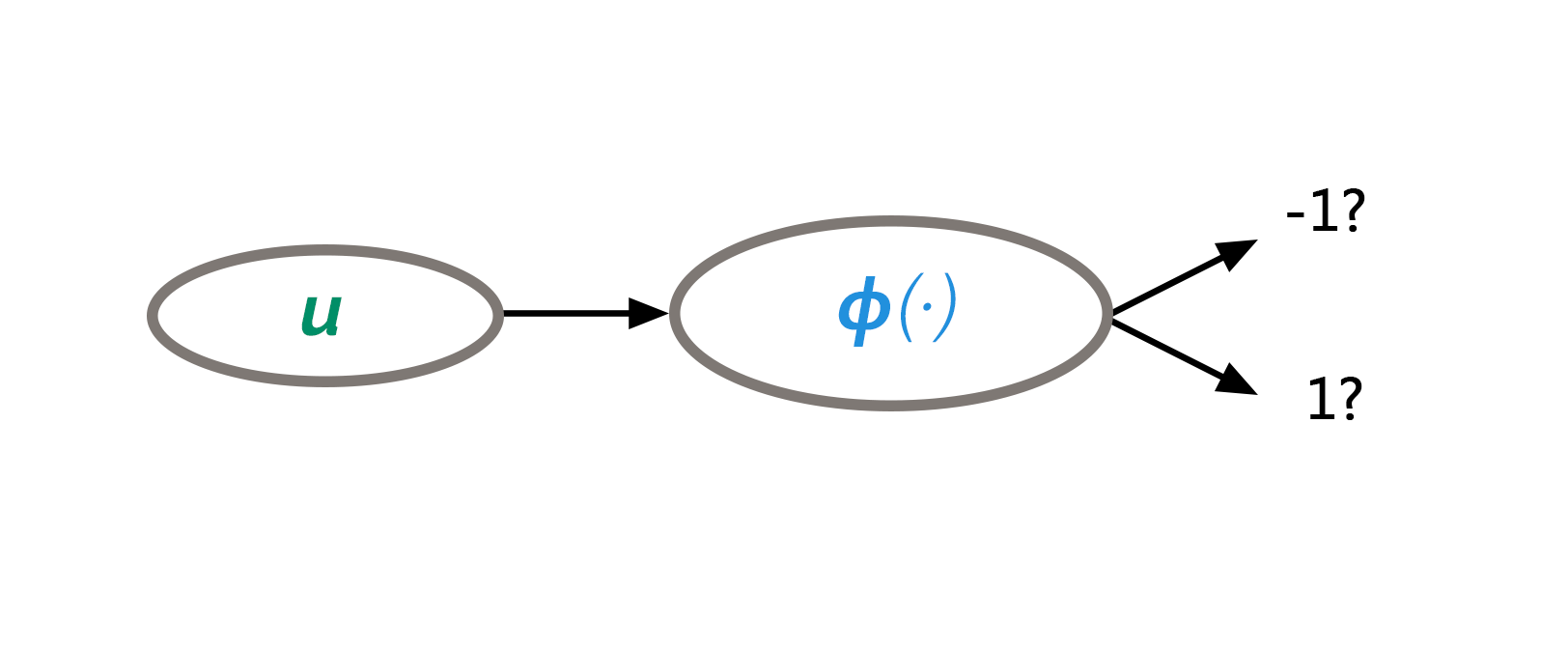
그러면 분류 문제는 주어진 데이터 \(\{(u_i,y_i)\}_{i=1}^N\)로부터 아래의 “인공지능” 함수를 찾는 것이 된다.
\begin{align*} \phi(u)\;:\;{\mathbb{R}}^d\to\{-1,1\} \end{align*}
다시 말해, 주어진 데이터를 바탕으로, 새로운 사진 (\(u\in{\mathbb{R}}^d\))의 동물을 잘 분류하는 함수 \(\phi(u)\)를 찾고자 한다. 이를 간단한 최소제곱법Least Squares 형태의 최적화 문제로 표현하면 다음과 같다(참고로 이외에도 수많은 다른 최적화 문제로 표현할 수 있다).
\begin{align*} minimize_{\phi}\; \sum_{i=1}^N[y_i – \phi(u_i)]^2\end{align*}
아쉽게도 위 문제에서 모든 함수 \(\phi\)에 대해서 최적화하는 것은 거의 불가능하며, 우리는 보통 그 범위를 좁혀서 알아본다. 그 좋은 예가 (\(x\)와 \(b\)를 매개변수Parameter로 하는) 아래의 선형 분류기Linear Classifier이며,
\begin{align*} \hat{\phi}(u;x,b) := sign(x^\top u – b) = \begin{cases}-1, & x^\top u – b < 0, \\ 1, & x^\top u – b \ge 0.\end{cases}\end{align*}
이 경우 분류 최적화 문제는 아래와 같이 간단해진다.
\begin{align*}minimize_{x\in{\mathbb{R}}^d, b\in{\mathbb{R}}} \;\sum_{i=1}^N\left[y_i – sign(x^\top u – b)\right]^2
\end{align*}
이를 조금 더 쉽게 풀기 위해 (이차함수 최적화 문제인) 아래의 선형 최소제곱법 최적화 문제를 고려하기도 한다.
\begin{align*}minimize_{x\in{\mathbb{R}}^d, b\in{\mathbb{R}}}\;\sum_{i=1}^N\left[y_i – (x^\top u_i – b)\right]^2\end{align*}
지금까지 강아지와 고양이를 분류하는 “인공지능” 선형 분류기 \(\hat{\phi}(u;x,b)\)를 찾는 방법에 대해 공부해 보았다. 하지만 아쉽게도 세상의 많은 현상은 선형적으로만 이해할 수 없기 때문에 비선형적인 모델이 필요하다.
그중 우리에게 익숙한 딥러닝 (혹은 인공신경망Artificial Neural Network을 이용한 머신러닝)이 현재 가장 좋은 성능을 내고 있고, 분류와 바둑을 비롯한 수많은 응용 분야에서 인간 이상의 우수한 결과를 내고 있다. 수많은 딥러닝 연구자들이 하루가 다르게 새로운 딥러닝 연구 결과를 쏟아내고 있기 때문에 안타깝게도 이 글에서 하나하나 다 설명할 수는 없고, 큰 그림에서 딥러닝 기반의 분류기가 어떻게 선형 분류기와 다른지 쉽게 설명해보겠다.
\(L\)개 층을 가진 인공신경망으로 이루어진 딥러닝 분류기는 일반적으로 다음과 같이 표현된다. \(L=1\)인 경우 선형 분류기의 형태가 된다는 점을 참고하자.
\begin{align*}\breve{\phi}(u;X_1, \ldots, X_L, b_1,\ldots, b_L)= \sigma_L(X_L{\sigma_{L-1}}\cdots\sigma_2(X_2\sigma_1(X_1u – b_1) – b_2)\cdots) – b_L)\end{align*}
여기서 함수 \(\sigma_1,\ldots\sigma_L\)은 신경망의 뉴런neuron 역할을 하는 특수한 함수로 정해진다.
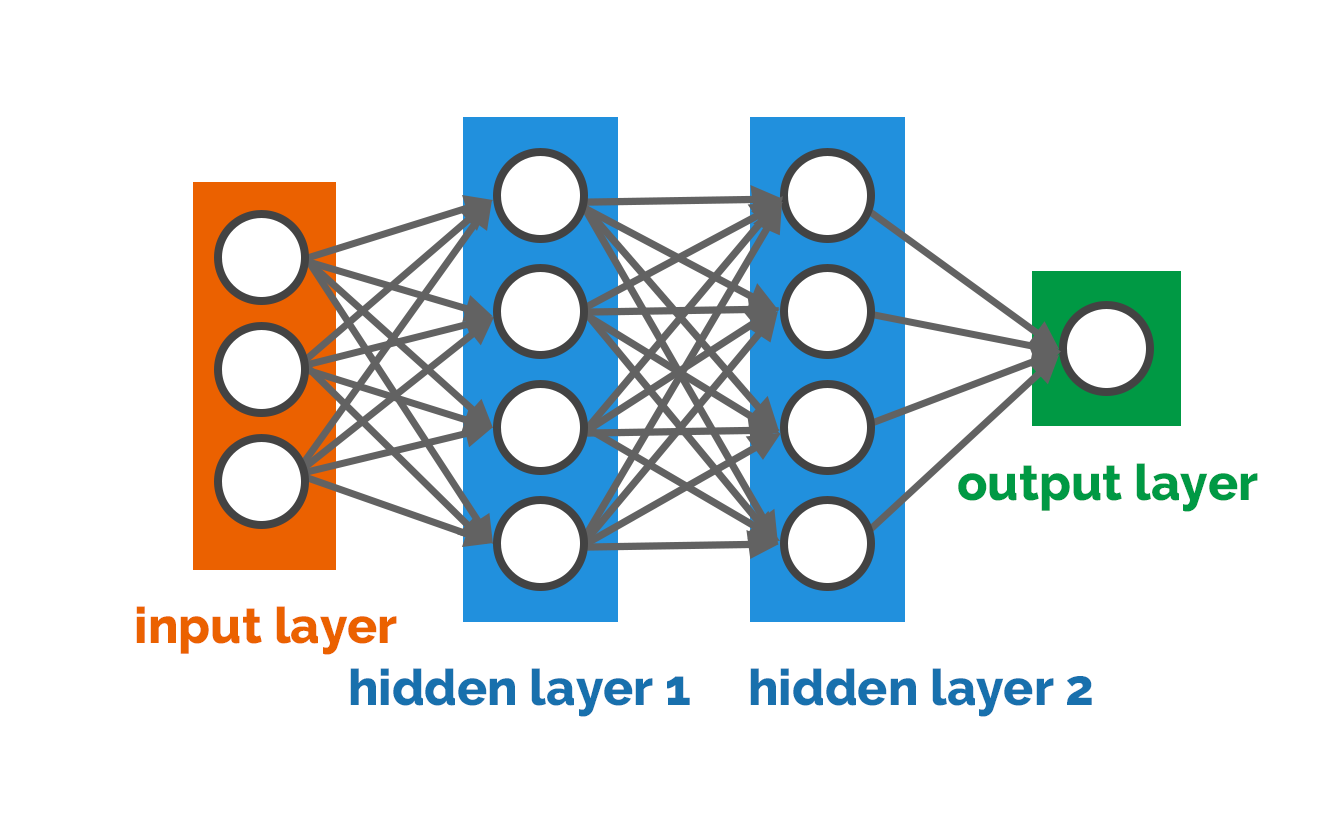
그리고 \(X_1,\ldots,X_L,b_1,\ldots,b_L\)의 후보집합 \(S\)를 어떻게 정하느냐에 따라 [그림6]과 같이 인공신경망 형태가 결정된다(자세한 내용은 생략하도록 하겠다). 이렇게 인공신경망 뉴런과 형태가 결정되면 아래의 분류 최적화 문제를 푸는 과정(혹은 인공신경망 학습 과정)만 남게 된다.
\begin{align*} minimize_{(X_1, \ldots, X_L, b_1,\ldots, b_L)\in S} \;\sum_{i=1}^N[y_i – \breve{\phi}(u;X_1,\ldots, X_{L-1}, x_L, b_1, \ldots, b_L)]^2\end{align*}
앞서 예로 든 간단한 여행계획 최적화 문제와는 달리, 위의 딥러닝기반 분류 최적화 문제를 비롯한 수많은 최적화 문제는 최적해를 한 번에 쉽게 구할 수가 없다(앞서 언급한 선형 분류 최적화 문제 역시 최적해를 한 번에 쉽게 구할 수 없는데, 딥러닝 최적화 문제에 비하면 상대적으로 쉬운 편이다). 이런 최적화 문제들을 풀기 위해서 반복 최적화 방법들이 몇백 년 전부터 뉴턴Isaac Newton, 코시Louis Augustin Cauchy를 비롯한 수학자들에 의해 개발되었다.
3. 반복Iterative 최적화 방법과 기계학습
반복 최적화 방법은 최적해를 반복적으로 근사하여 최적해를 찾는다. 그 중 세 가지의 기본적인 최적화 방법들을 소개하고 이들이 기계학습에서 어떻게 쓰이는지 이야기하겠다.
3.1. 뉴턴 방법
뉴턴 방법은 이창옥 교수님의 HORIZON 기고문인 “계산수학의 태동과 발전”에서 방정식을 푸는 방법으로 이미 소개되었다. 여기서는 이 방법이 어떻게 최적화에서 쓰이는지 설명하겠다.
1669년 뉴턴은 방정식 \(g(x) = 0\)의 해 (\(x_*\in{\mathbb{R}}\))를 구하기 위해 아래의 방법으로 수열Sequence \(\{x_0,x_1,\ldots\}\)을 생성했다.
\begin{align*}x_{k+1} = x_k – \frac{g(x_k)}{g'(x_k)}, \quad k=0,1,\ldots.\end{align*}
이는 방정식 \(g(x) = 0\)을 \(x_k\) 지점에서 일차방정식 \(g(x_k) + g'(x_k)(x-x_k) = 0\)으로 근사한 결과이며, 뉴턴 방법은 이를 반복적으로 수행하여 \(g(x)=0\)의 해를 찾는다.
뉴턴 방법은 최적화 문제를 풀기 위해서도 쓰이는데, 이는 최적해 (\(x_*\in{\mathbb{R}}^d\))가 다음의 방정식을 만족한다는 것에서 비롯된다.
\begin{align*}\nabla f(x) =0\end{align*}
뉴턴 방법을 여기에 적용하면 방정식 \(\nabla f(x) = 0\)을 \(x_k\) 지점에서 일차방정식 \(\nabla f(x_k) + \nabla^2 f(x_k)(x – x_k) = 0\)으로 반복적으로 근사하는 것과 같고, 이는 아래의 방법으로 수열 \(\{x_0,x_1,\ldots\}\)를 생성하는 것과 같다.
\begin{align*}x_{k+1} =x_k – [\nabla^2 f(x_k)]^{-1}\nabla f(x_k),\quad k=0,1,\ldots\end{align*}
이것은 최적화 문제에서 \(f(x)\)를 \(x_k\) 지점에서 이차함수
\begin{align*}f(x_k) + \nabla f(x_k)^\top(x – x_k) + \frac{1}{2}(x-x_k)^\top\nabla^2 f(x_k) (x – x_k)\end{align*}
로 반복적으로 근사하는 방법과 같다.
뉴턴 방법은 방정식과 최적화의 해를 구하기 위해 기본적으로 많이 쓰이고 있다. 하지만 최근 기계학습을 포함한 최적화 문제들의 차원이 상당히 커지면서 뉴턴 방법의 계산이 비효율적인 경우가 많아졌다. 이는 차원이 큰 최적화 문제에서 헤시안Hessian \(\nabla^2 f(x_k)\)와 뉴턴 방법의 업데이트 \([\nabla^2 f(x_k)]^{-1}\nabla f(x_k)\) 계산이 비효율적이기 때문이다. 또한 병렬 계산이 장점인 GPUGraphics Processing Unit을 뉴턴 방법이 효율적으로 사용하기가 쉽지 않다. 그래서 상대적으로 효율적인 그리고 병렬 계산에 적합한 다음 두 가지의 반복 최적화 방법이 최근 더 각광받고 있다.
3.2. 경사하강Gradient Descent법
다음의 경사하강법은 코시가 천체의 움직임을 계산하기 위해 1847년에 처음으로 개발한 것으로 알려져 있다.
\begin{align*}x_{k+1} = x_k – \alpha_k \nabla f(x_k),\quad k=0,1,\ldots\end{align*}
경사하강 업데이트 크기를 결정하는 \(\alpha_k\) 값에 따라 수열 \(\{x_0,x_1,\ldots\}\)는 최적해로 수렴하거나 발산할 수 있고, 수렴하는 경우에 그 값은 수렴속도에 영향을 준다. 따라서 주어진 문제에 따라 \(\alpha_k\)를 잘 정하는 것이 중요하며, 이 값은 기계학습 분야에서는 학습속도Learning Rate라 불리며 중요하게 다뤄진다.
뉴턴 방법과의 차이점은 헤시안을 사용하지 않는다는 점이다. 그래서 계산이 효율적이지만 수렴속도가 느린 단점이 있다. 이런 단점을 해결하기 위해 많은 고속화Acceleration 방법들이 개발되었으며 (이창옥 교수님의 “계산수학의 태동과 발전” 본지 기고문에서 언급된) 켤레경사Conjugate Gradient법이 그 하나의 예이다. 켤레경사법은 볼록한 이차함수 \(f(x)\)의 경우에 수렴속도가 향상되는 것이 증명되었는데, 앞서 봤듯이 많은 최적화 목적함수는 비선형적이기 때문에 더 일반적인 고속화의 개발이 필요했다.
1964년 폴리악Boris Polyak은 볼록Convex하고 두 번 연속 미분 가능한 목적함수 \(f(x)\)에 대해 빠른 수렴속도를 지닌 다음의 헤비볼Heavy-ball법을 개발하였다.3
\begin{align*}x_{k+1} = x_k – \alpha_k \nabla f(x_k) + \beta_k(x_k -x_{k-1}), \quad k=0,1,\ldots\end{align*}
이는 모멘텀Momentum \({\beta_k}(x_k – x_{k-1})\)을 더하여 고속화한 방법이기 때문에 모멘텀Momentum법으로도 불리며, 현재 기계학습 최적화에서 가장 널리 쓰이는 고속화 방법 중 하나이다. 물론 딥러닝 최적화 문제는 비볼록Non-convex하기 때문에 모멘텀법이 해당 문제에서 수렴속도가 빠르다는 이론적 근거는 아직 조금 부족하다. 하지만 실험적으로 빠른 결과가 확인되기 때문에 많은 딥러닝 연구자들이 선호하는 방법이다.
3.3. 확률적 경사하강Stochastic Gradient Descent법
앞서 분류 최적화 문제에서 보았듯이 기계학습을 비롯한 많은 최적화 문제는 다음과 같이 목적함수를 여러 함수의 합으로 표현할 수 있다. 분류 최적화 문제의 경우 \(f_i(x) = [y_i – \hat{\phi}(u_i;x)]^2\)로 정하면 된다.
\begin{align*}minimize_{x\in S}\; \left\{f(x) := \sum_{i=1}^N f_i(x)\right\}\end{align*}
이런 형태의 최적화 문제를 빠르게 해결하기 위해 로빈스Herbert Robbins와 몬로Sutton Monro는 1951년 다음의 확률적 경사하강법을 제시하였다.4
\begin{align*}x_{k+1} = x_k – \alpha_k \nabla f_{i_k}(x_k), \quad k=0,1,\ldots\end{align*}
여기서 매번 \(i_k\in\{1,\ldots,N\}\)를 확률적으로 선택하고, 경사하강법의 \(\nabla f(x_k)\) 대신에 \(\nabla f_{i_k}(x_k)\)의 정보만을 이용한다. 분류 최적화 문제를 예로 들면, 한번 업데이트 할 때마다 하나의 데이터 \((u_{i_k},y_{i_k})\)를 이용해서 학습한다고 볼 수 있다. 따라서 이 방법의 장점은 한번 업데이트할 때 계산량이 경사하강법보다 \(N\) 분의 \(1\) 만큼 작다는 점이다. 물론 그만큼 수렴속도가 느려지는데, 많은 경우에 이득이 더 큰 것으로 알려졌고, 그래서 기계 학습에서 가장 널리 쓰이고 있다. 여기에 고속화를 위해 모멘텀법을 추가한 방법 역시 많이 쓰이고 있다.
이뿐만 아니라 확률적 업데이트를 이용하는 확률적 경사하강법이 경사하강법보다 지역 최적해를 잘 벗어나서 전역 최적해를 잘 찾는 것으로 실험적으로 많이 확인된 점이, 확률적 경사하강법이 기계학습에서 더 널리 쓰이도록 크게 기여하고 있다. 참고로 AlphaGo의 학습 (최적화)에서도 확률적 경사하강법이 쓰였다.
지금까지 기계학습의 바탕이 되고 있는 최적화 이론에 대해 간략히 이야기해보았다. 특히 인간 두뇌의 신경망에서 영감을 얻은 인공신경망을 이용한 딥러닝은 반복 최적화 방법을 이용하여 학습한다는 것을 알 수 있었다. 물론 딥러닝을 비롯한 최신 최적화 문제들은 이 글에서 소개한 내용에 비해 훨씬 더 다양하고 복잡하다. 그런 어려운 최적화 문제들을 해결하기 위해 앞서 언급한 세 가지의 방법 외에 다양한 반복 최적화 방법들이 개발되었고 현재 활발히 연구되고 있다. 이와 관련해서 하나 언급하고 싶은 것은, 이 글의 반복 최적화 방법들은 \(f(x)\)가 모든 점에서 미분가능하다는 가정을 당연히 여겼고 후보집합 \(S\)에 대한 고려를 하지 않았다는 것이다. 하지만 대다수의 딥러닝 혹은 최신 최적화 문제들의 목적함수 \(f(x)\)는 모든 점에서 미분 가능하지는 않고 특정한 \(S\)가 주어지기 때문에, 이 글에서 소개한 반복 최적화 방법들을 그대로 사용할 수는 없다.
최적화 분야의 중요한 연구 방향 중 하나는 이와 같이 다양한 수학적 가정 하의 최적화 문제를 잘 이해하고, 그 최적해를 어떻게 효율적으로 찾을 것인지 고민하는 것이다. 기회가 주어진다면 이에 대한 조금 더 깊은 이야기를 본지에서 한번 소개하고 싶은 마음이 있다.
AlphaGo의 성공을 비롯하여 인공지능이 나날이 발전하면서 최적화에 바탕을 둔 인공지능이 실제 인간 두뇌의 수준까지 발전할 수 있을지 많은 이들이 궁금해하고 있다. 그런데 과연 인간 두뇌의 신경망도 반복 최적화 방법과 비슷한 방식으로 세상을 이해하고 공부하는 것일까? 언젠가는 기계학습과 뇌과학의 발전이 이 질문에 대한 해답을 알려 줄 수 있으리라 믿고 있으며, 그 과정에서 최적화 이론이 분명 도움이 될 것이라 생각한다.