트럼프 카드를 몇 번 섞어야 공평한 카드놀이를 할 수 있을까?

우리는 52장의 카드로 이루어진 트럼프 카드로 다양한 카드놀이를 한다. 그때마다 게임이 공평하게 진행되리라는 기대를 가지고 카드를 열심히 섞는다. 가장 대중적인 방식은 아래 그림처럼 카드를 두 묶음으로 나누어 한 장씩 내리면서 섞는 셔플^{riffle shuffle}이라는 방식이다.

그런데, 한 번쯤 이런 질문을 해볼 수 있다.

“도대체 몇 번의 셔플을 해야 카드가 충분히 섞일 것인가?”

이 문제에 답을 하기 전에 카드를 섞는 행위의 본질을 생각해 볼 필요가 있다. 카드를 섞는 것은 하나의 무작위화^{randomization} 과정이라고 볼 수 있다. 무작위화 과정의 대표적인 예로는 우리가 어렸을 때부터 종종 겪어왔던 동전 던지기, 주사위 던지기, 윷 던지기 등이 있다. 두 명 중 오늘 점심값을 낼 사람을 정하기 위해 동전 던지기를 할 때, 동전을 던지는 사람이 동전을 충분히 높게 던지지 않는다면 점심을 사게 된 사람은 분명 항의를 할 것이다. 윷놀이에서 윷을 높게 던지지 않고 사뿐히 내려놓아 윷놀이의 모가 나왔다면 역시 상대가 항의를 할 것이다. 이러한 항의는 무작위화 과정이 충분히 진행되지 않았기 때문에 발생하는 것이다. 즉, 동전, 주사위, 윷 등을 던져서 공평한 결과를 얻기 위해서는 이들을 높이 던지는 “무작위화 과정”이 충분히 진행되어야 한다는 것을 우리는 이미 경험적으로 알고 있는 것이다. 무작위화 과정은 우리가 이러한 놀이의 결과들을 신뢰하게끔 하는 가장 기본이 되는 것이다.

다시 카드놀이로 돌아와 보자. 카드놀이의 무작위화 과정은 바로 셔플과 같은 행위를 하여 카드를 잘 섞어주는 과정일 것이다. 그렇다면 셔플을 몇 번을 해야 이러한 무작위화 과정이 충분히 진행되어 공평한 카드 놀이를 보장할 수 있을까?

1990년 1월 9일, 뉴욕타임즈에는 “In shuffling cards, 7 is winning number”라는 제목의 기사가 실렸다. 기사의 내용은 놀랍게도 52장의 카드가 충분히 섞이려면 셔플을 7번 해야 한다는 것이었고, 만약 셔플을 7번보다 적게 하면 사실상 카드가 섞이지 않아 공평한 게임을 보장할 수 없다는 것이었다. 즉, 셔플을 진행할 때, 6번째까지는 카드가 거의 섞이지 않다가 7번째 셔플이 진행되는 순간에 갑작스럽게 카드가 다 섞인다는, 다소 직관적이지 않은 내용을 포함하고 있는데 이는 논문[1]에서 Bayer와 Diaconis가 증명한 내용이다. 이러한 현상은 마르코프 체인^{Markov chain}이 발현하는 컷오프^cutoff 현상의 대표적인 예이다.

마르코프 체인

위의 내용을 확률론의 용어들을 통해 좀 더 자세히 설명하기 위해 먼저 마르코프 체인이라는 개념을 소개하고자 한다.

유한 집합 \(S\)에 대해 \(p:S\rightarrow[0,\,1]\)이, \(\sum_{s\in S} p(s)=1\)을 만족한다면 이러한 \(p\)를 \(S\)에서 정의된 확률 분포라 한다. 이를 확률 분포라고 하는 이유는 \(p(s)\)를 원소 \(s\)가 선택될 확률이 라고 생각할 수 있기 때문이다. 이를 좀 더 구체적으로 설명하기 위해 무작위 변수^{random variable}라는 개념을 도입한다. 변수 \(X\)가 \(S\)에서 정의된 무작위 변수라는 것은 \(X\)가 \(S\)의 원소 중 임의의(무작위의) 하나의 값을 가진다는 것을 의미한다. 특히 \(X\)의 분포가 앞서 정의한 확률 분포 \(p\)라는 것은 \(X\)가 가지는 임의의 값이 \(s\in S\)일 확률이 \(p(s)\)가 된다는 것을 의미한다. 이를 \(P[X=s]=p(s)\)로 나타낸다. 예를 들어 공평한 주사위를 던져서 나온 눈을 \(X\)라 하면, \(X\)는 \(S=\{1,\,2,\,3,\,4,\,5,\,6\}\)에서 정의된 무작위 변수로, \(X\)가 따르는 확률분포 \(p\)는 \(p(1)=p(2)=\cdots =p(6)=1/6\)인 \(p:S\rightarrow [0,\,1]\)이 된다.

마르코프 체인이란 무작위 변수들 \(X_1 ,\,X_2 ,\,\dots\)로 이루어진 무작위 변수들의 수열로서, 각 \(t\)에 대해 \(X_{t+1}\)의 분포가 오직 \(X_t\)의 값에 의해서 결정되는 것을 뜻한다. 이를 좀 더 자세히 정의하기 위해, 먼저 어떤 \(q:S\times S\rightarrow \mathbb{R}\)이 존재하여 각 \(s\in S\)에 대해 \(\sum_{s’ \in S}q(s,\,s’)=1\)을 만족한다고 하자. 무작위 변수들의 수열 \((X_t)_{t=1}^\infty\)이 \(q\)를 핵^kernel으로 가지는 마르코프 체인이라 함은 \(X_t = s\)일 때, \(X_{t+1}=s’\)일 확률이 \(q(s,\,s’)\)가 됨을 뜻한다. 마르코프 체인의 특징은 \(X_1\)의 값이 결정되면 \(X_2\)의 분포가 결정되고, 이 분포로부터 \(X_2\)를 선택하면 다시 \(X_3\)이 결정되는 식으로 무작위 변수의 값이 하나씩 바로 전 단계의 무작위 변수로부터 결정된다는 것을 뜻한다.

마르코프 체인 \((X_t)_{t=1}^\infty\)에서 \(X_1\)의 분포가 \(p\)라 하자. 이때, \(X_2\)가 \(s’\)일 확률을 구해보면 다음과 같이 됨을 쉽게 생각할 수 있다.\[\sum_{s\in S}p(s)q(s,\,s’)\]즉, \(X_1\)의 분포 \(p\)와 핵 \(q\)로부터 \(X_2\)의 분포도 계산할 수 있는 것이다. 이렇게 구한 \(X_2\)의 분포가 만약 \(X_1\)의 분포인 \(p\)와 같다면 귀납적으로 모든 \(X_3,\,X_4,\,\dots\)의 분포가 모두 \(p\)가 됨을 알 수 있다. 이러한 확률 분포 \(p\)가 존재한다면, 이를 이 마르코프 체인의 불변 분포^{invariant distribution}라고 한다. 마르코프 체인에서 불변 분포는 매우 중요한 개념이다. 자세히 설명하지는 않겠지만, 마르코프 체인이 주기성이 없고^aperiodic, 기약^irreducible이면 에르고딕^ergodic하다고 하는데, 이 경우 마르코프 체인의 불변 분포가 유일하게 존재함이 알려져 있다.

마르코프 체인 몬테 카를로^{Markov chain Monte Carlo, MCMC}

다음으로 마르코프 체인의 분포의 수렴을 알아보자. 이를 설명하기 위해 두 확률 분포 \(p_1,\,p_2\)사이의 거리를 \[\Vert p_1 – p_2 \Vert =\frac{1}{2} \sum_{s\in S} |p_1 (s)-p_2(s)|\]로 정의하자. 여기서 우변에 \(1/2\)를 곱하는 이유는 여러 가지가 있지만 대표적으로는 두 분포 사이의 거리의 최댓값이 \(1\)이 되게 표준화하기 위해서이다. 즉, 두 확률분포 사이의 거리가 \(0\)에 가까워질수록 두 분포는 서로 비슷한 분포라고 볼 수 있으며, \(1\)에 가까워질수록 그 반대라고 생각할 수 있다.                                      

마르코프 체인 \((X_t)_{t=1}^\infty\)이 \(X_1 =s\)를 만족할 때, \(X_t\)의 분포를 \(p_s^{(t)}\)로 나타내자. 즉, \(P[X_t = s’ \;\text{when}\;X_1=s]=p_s^{(t)}(s’)\)인 것이다. 예를 들어 \(p_s^{(2)}(s’)=q(s,\,s’)\)가 된다.

정리 1. 마르코프 체인 \((X_t)_{t=1}^\infty\)이 에르고딕일 때 그 불변 분포를 \(p\)라 하자. 이때, 임의의 \(s\in S\)에 대해 다음이 성립한다.\[\lim_{n\rightarrow \infty} \Vert p_s^{(t)} -p \Vert =0\]정리 1은 \(X_1\)의 값을 임의의 에서 시작하더라도, \(t\)가 커지면서 \(X_t\)의 분포는 마르코프 체인의 불변 분포 \(p\)로 수렴한다는 것을 의미한다.

만약 \(S\)가 매우 큰 집합이고, \(p\)가 \(S\)에서 정의된 복잡한 확률 분포이면 분포 \(p\)를 따르는 무작위 변수 \(X\)를 컴퓨터 등으로 생성하는 것은 쉽지 않은 문제인 경우가 많다. 이때, 다음과 같이 정리 1을 활용하는 방법이 가능하다.

먼저 분포 \(p\)를 불변 분포로 가지는 \(S\)위에서의 에르고딕한 마르코프 체인을 하나 생성한 뒤, 이 마르코프 체인을 임의의 점 \(X_1 =s\)에서 시작하는 것이다. 이때, \(X_2,\,X_3,\,\dots\) 등을 단계적으로 결정하여 충분히 큰 \(t\)에 대해 \(X_t\)를 택하자. 정리 1에 의해 \(X_t\)의 분포 \(p_s^{(t)}\)는 \(t\)가 커지면서 \(p\)로 수렴한다는 사실을 고려하면, 우리는 \(p\)와 유사한 분포를 가지는 무작위 변수 \(X_t\)를 근사적으로 추출할 수 있다. 이러한 방법을 마르코프 체인 몬테 카를로^{Markov chain Monte Carlo, 이하 MCMC}라고 한다.

컷오프 현상

앞서 설명한 MCMC 기법의 관점에서 정리 1을 다시 살펴볼 때, 가장 주요한 문제는 \(t\)가 얼마나 커야 \(\Vert p_s^{(t)} – p\Vert\)의 값이 \(0\)에 충분히 가까워지는지 아는 것이다. 이를 판단하기 위해 \[d(t)=\max_{s\in S} \Vert p_s^{(t)} – p\Vert\]라 정의하자. 이 값은 \(s\in S\)들에 대해 \(\Vert p_s^{(t)} – p\Vert\)가 가질 수 있는 가장 큰(즉, 가장 안좋은) 값을 의미한다. 이 값이 \(0\)에 충분히 가깝게 되는 \(t\)를 사용해야 MCMC 기법이 원활하게 작동할 수 있는 것이다.

이러한 \(t\)를 찾기 위해 \(d(t)\)의 그래프를 생각해 볼 필요가 있다. 간단한 수학적 고찰을 통해 \(d(t)\)가 \(t\)에 대한 감소함수임을 알 수 있으며, 정리 1은 \(\lim_{t\rightarrow \infty}d(t)=0\)임을 의미한다. 또한, 일반적으로 \(S\)가 충분히 큰 집합이면 \(d(0)\)의 값은 \(1\)에 가까운 값이 되기 때문에, 통상적으로 \(d(t)\)의 그래프는 \(1\)근처에서 시작하며 \(t\)가 증가함에 따라 감소하여 \(0\)으로 수렴하는 형태임을 예측할 수 있다.

컷오프 현상이란 \(d(t)\)의 그래프가 옆의 그림과 같이 어떠한 \(t_0\)을 전후로 아주 짧은 구간에서 급격히 근처에서 근처로 하강하는 경우를 뜻한다. 수학적으로 이야기하면 어떤 \(w_0\ll t_0\)이 존재하여 \(d(t_0 + w_0 )\simeq 0\), \(d(t_0 – w_0) \simeq 1\)이 됨을 뜻한다.

만약 MCMC가 이와 같은 현상을 보인다고 하자. 만약 \(t<t_0 –w_0\)이라면 \(d(t)\simeq 1\)이 되는데 이는 시점 \(t\)에서 추출한 \(X_t\)의 분포가 불변 분포 \(p\)와 거리가 멀다는 것을 의미하기 때문이다. 반대로 \(t>t_0 + w_0\)이면 \(X_t\)의 분포는 불변 분포 \(p\)와 충분히 가까운 분포가 되어 MCMC가 성공적으로 작동하게 된다. 즉, \(t_0\)은 MCMC가 성공적으로 작동하기 위한 분기점이 되는 것이다. 이는 특별한 현상으로 보이지만 의외로 수많은 확률 시스템에 공통으로 발현되는 현상임이 알려져 있다. 그중 가장 대표적인 예가 앞서 살펴본 카드 셔플이다.

카드 섞기의 수학적 모형과 컷오프 현상

52장의 카드 대신, 일반적으로 \(n\)장의 카드를 셔플하는 것을 생각해보자. 카드 셔플을 수학적으로 설명하는 것은 다음과 같은 Gilbert-Shannon 모형(1995)이 알려져 있다.

Gilbert-Shannon 모형

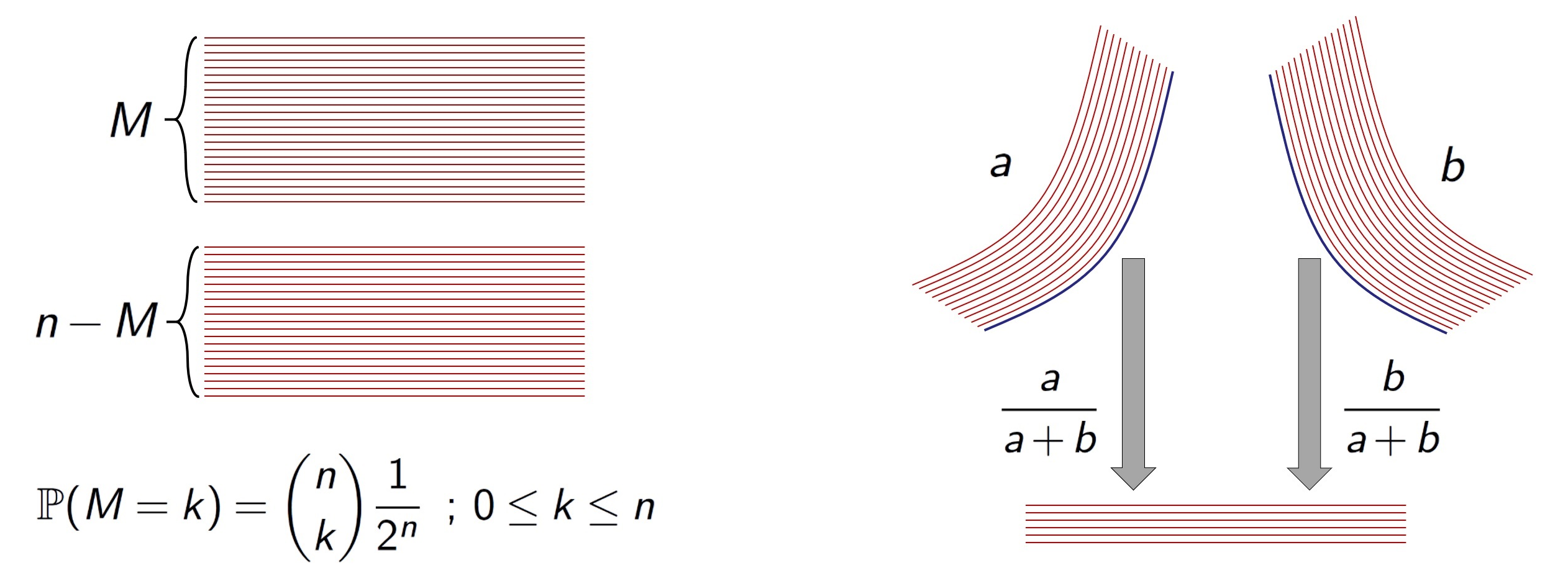
1. 카드를 두 더미 \(M\)장과 \(n-M\)장으로 나눈다. 이때 \(M\)은 무작위 변수로서 이항분포를 따른다고 하자. 즉, 다음이 성립한다고 한다.\[P[M=k]={n \choose {k}} \frac{1}{2^n} \;\;;\;k=0,\,1\,\dots,\,n.\]이러한 \(M\)은 공평한 동전을 \(n\)번 던졌을 때 나온 앞면의 개수와 같은 분포를 가진다. 따라서 \(M\)은 약 \(n/2\)에 집중된 무작위 변수로 \(\sqrt{n}/2\)의 표준편차를 가지는데, 이는 실제로 사람 역시 \(n\)장을 거의 반으로 나누지만 다소간의 오차가 있게 되는 상황을 잘 모델링한다고 생각할 수 있다.
2. 두 더미의 카드를 하나로 합친다. 이때 왼손과 오른손에 남은 카드가 각각 \(a\)장, \(b\)장이라면 왼손의 카드를 먼저 내릴 확률은 \(\frac{a}{a+b}\), 오른손의 카드를 먼저 내릴 확률은 \(\frac{b}{a+b}\)이다. 이는 상대적으로 많은 카드가 남은 쪽에서 먼저 카드를 내릴 확률이 높음을 반영한 것이다.
3.  

이처럼 1, 2의 과정을 이용한 셔플을 반복한다고 하자. 처음 카드의 배열을 \(X_1\)이라 하고 이를 셔플하여 얻는 배열을 \(X_2\)라 하자. 귀납적으로 카드 배열 \(X_t\)를 셔플하여 얻는 배열을 \(X_{t+1}\)이라 하자. 그러면 \(X_{t+1}\)의 분포는 (매우 복잡하지만) 오직 \(X_t\)에만 의존함이 자명하고, 이로부터 \((X_t)_{t=1}^\infty\)는 \(S_n\)에서 정의된 마르코프 체인임을 알 수 있다. 여기서 \(S_n\)은 \(n\)장의 카드를 배열하여 얻을 수 있는 모든 더미들의 집합으로 \(|S_n| =n!\)이다. 이 마르코프 체인이 에르고딕함은 쉽게 확인할 수 있고, 따라서 불변 분포는 유일하게 존재하는데, 이 경우는 그 불변 분포 \(u_n\)이 \(S_n\)의 각 원소들이 선택될 확률이 \(1/n!\)로 모두 동일한 고른 분포^{uniform distribution}가 된다.

공평한 카드놀이가 되도록 카드를 섞는 것은 무엇을 의미할까? 이는 바로 앞서 언급한 \(S_n\)에서 정의된 고른 분포 \(u_n\)과 비슷한 분포를 추출하는 것으로 생각할 수 있다. 이때, 앞서 Gilbert-Shannon 모형으로 정의된 마르코프 체인 \((X_t)_{t=1}^\infty\)는 \(u_n\)을 불변 분포로 가지므로 카드를 반복적으로 셔플하는 것은 다름 아닌 이 분포 \(u_n\)을 추출하기 위한 MCMC로 이해할 수 있다. 그리고 카드를 몇 번 셔플해야 이 고른분포에 가까운 분포를 추출할 수 있는지 묻는 것은 앞서 고려한 것처럼 해당하는 MCMC가 잘 작동하기 위한 \(t\)의 값을 찾는 것을 의미한다.

이 카드 셔플에 해당하는 MCMC는 컷오프 현상을 가짐이 [1]에서 증명되어 있다. 특히 \(t_0 = (3/2)\log_2 n\)이라 하고 \(w_0 =4\)로 하면 \(d(t_0-w_0)>0.99\)인 반면 \(d(t_0+w_0)<0.01\)임이 증명되었다. 따라서 \((3/2)\log_2 n –4\)번보다 적게 셔플을 하면 카드가 사실상 전혀 섞이지 않는 반면, \((3/2)\log_2 n +4\)번보다 많이 셔플을 하면 얻게 되는 카드의 분포는 고른 분포 \(u_n\)과 상당히 가까운 분포가 되어 공평한 카드놀이를 보장해주게 됨을 알 수 있다.

다시 처음 서론에 언급된 \(n=52\)의 경우를 살펴보자. 이 경우 \(3/2\log_2 52 \simeq 8.5\)이므로 \(5\)번에서 \(12\)번 셔플하는 중간에 카드가 갑자기 셔플하게 됨을 알 수 있고, 특히 \(4\)번의 셔플은 공평한 카드놀이를 보장하기에는 현저히 적은 횟수임을 알 수 있다. 좀 더 자세한 답을 하기 위해, 이 경우에는 \(t\)값에 따른 \(d(t)\)의 값을 실제로 다음과 같이 근사적으로 계산할 수 있다.

그렇다면 공평한 게임을 보장받기 위한 최소의 셔플 횟수는 몇 번인가? 이는 가치판단의 영역이지만 최소한 \(6\)번의 경우는 \(d(6)=0.61\)임을 볼 때 불충분함은 알 수 있다. 반면 \(8\)번의 경우는 \(d(8)=0.16\)으로 즐기기 위한 카드놀이의 수준에서는 충분히 공정성을 담보해 줄 것으로 보인다. \(7\)번에서 얻어지는 \(0.33\)이 충분한지는 사람마다 다르게 생각할 수 있다는 것이 필자의 의견이다. 종합할 때 셔플을 \(7\)번에서 \(8\)번 정도 해야 카드가 충분히 섞인다고 답변을 할 수 있다. 물론 이 결과는 Gilbert-Shannon의 모형을 받아들일 때에 국한된 결과임을 다시 한번 강조한다.

컷오프 현상과 통계역학

컷오프 현상에 대한 연구는 카드 셔플 등에서 이 현상이 발견된 90년대 이후 한참이 지난 2000년대 말에 이르러서야 새로운 연구의 돌파구가 마련되었다. 이후 많은 연구자들에 의해 이 현상이 고온 상태의 상호작용 입자시스템^{interacting particle system}, 자기 시스템^{ferromagnetic system} 등 통계역학의 모형들에서 공통적으로 발현되는 현상임이 밝혀지고 있다. 최신 연구와 관련하여서는 [2][3][4][5][6][7] 등을 참조할 수 있다.

이러한 통계역학의 모형에서 정리 1에 따라 시스템의 분포가 불변 분포로 수렴하는 것은 불균형상태^{non-equilibrium state}에서 시작한 시스템이 균형상태^{equilibrium state}로 수렴하는 것을 뜻한다. 따라서 \(d(t_0)\)이 \(0\)에 근접해지는 \(t_0\)까지의 시간이 바로 이러한 수렴에 소요되는 시간이다. 고온의 경우 이 수렴이 비교적 빨리 나타나며 더 나아가 컷오프 현상을 발현하며 갑작스럽게 나타나게 된다. 반대로 저온의 경우 이 수렴이 대단히 천천히 나타나게 되는데 이를 메타안정성^{metastability}이라고 한다. 이때, 많은 모형들이, 어떤 온도 \(T_c\)에 대해, 온도가 \(T_c\)보다 높은 고온에서는 컷오프현상을, \(T_c\)보다 낮은 저온에서는 메타안정성을 보이는 일종의 상전이현상을 보이는데, 이러한 현상들을 아우르는 복합적인 연구들은 지금도 다양한 통계역학 모형들에 대해 활발하게 이루어지고 있다.