6월의 퍼즐에 참여해주신 모든 분들께 감사드립니다!
6월의 퍼즐 정답자는 조강진, 최지원님입니다.
(정답과 함께 좋은 해설을 제출해주신 조강진님께서 정답자로 선정되셨으며, 조강진님께서 기존에 정답자로 선정되셨기 때문에 이외 정답을 제출해주신 최지원님을 함께 선정하였습니다.)
이 문제는 영국의 과학기술 분야 주간지인 <뉴 사이언티스트New Scientist> 1977년 3월 24일 자에 연재된 퍼즐 코너 <Tantalizer>의 493번 문제인 “Prize guys”를 각색한 것이다. Tantalizer는 영국 이스트앵글리아 대학University of East Anglia의 철학과 교수였던 마틴 홀리스Martin Hollis가 1967년부터 1977년까지 총 500회를 연재하였다.
문제에서 제시된 상황을 보면, A가 다른 종목보다 넓이 미로(M)에서 순위가 낮았다고 했으므로, A는 이 종목에서 2위나 3위를 차지했음을 알 수 있다. 이것을 A-M2와 A-M3으로 나타내자.
A-M2인 상황이라면 A-S1, A-G1, 즉 A는 스도쿠(S)와 게임 역추적(G)에서 모두 1위가 되어야 한다. 따라서 스도쿠와 게임 역추적에서는 B와 C가 2위와 3위를 나누어 차지하게 된다. 이 상황에서 B가 게임 역추적보다 스도쿠에서 순위가 더 높다는 사실을 C가 알았다는 것은, C-S3, 즉 C가 스도쿠에서 3위여서 B-S2, 즉 B가 스도쿠에서 2위라는 것을 뜻한다. 동시에 B-G3이고 C-G2가 된다.
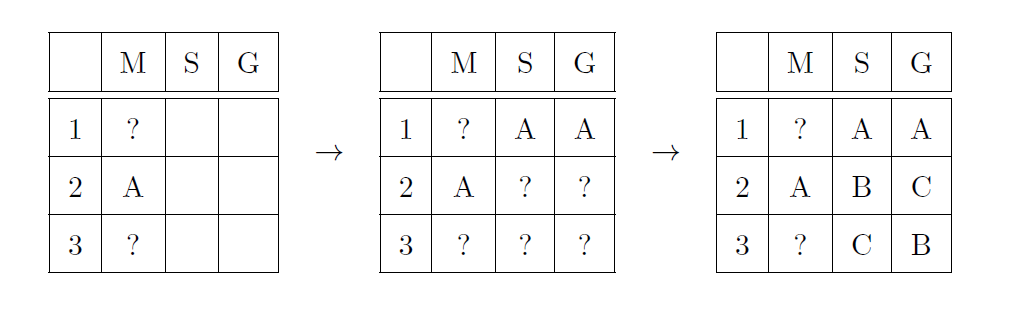
A-M3인 상황이라면 A는 스도쿠와 게임 역추적에서 1위나 2위가 되어야 한다. 만약 C가 스도쿠에서 2위를 했다면, 스도쿠 3위는 B가 될 수밖에 없으므로, B가 게임 역추적보다 스도쿠에서 순위가 더 높다는 사실에 부합하지 않는다. 따라서 C-S3이 된다. 이 상황에서 B가 스도쿠에서 순위가 더 높다는 사실을 확신하려면, C가 게임 역추적에서 2위를 하여 B가 게임 역추적에서 3위를 하는 경우가 있으나 이때에도 스도쿠에서 누가 1위인지는 결정할 수 없다.
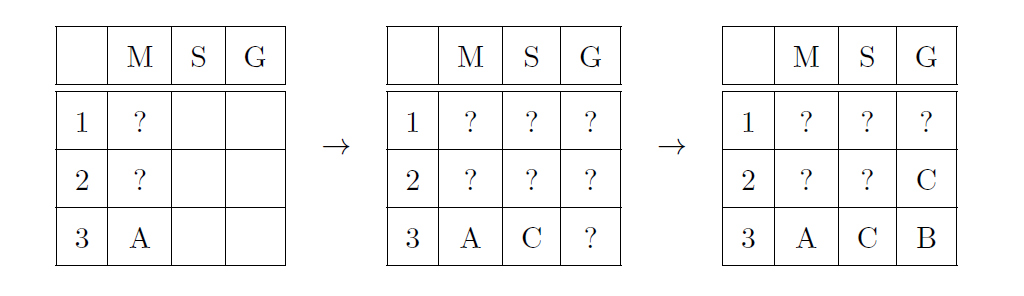
이상의 결과로부터 A-M2일 때 A-S1, B-S2, C-S3, A-G1, B-G3, C-G2인 경우만 가능하며, A가 넓이 미로에서 3위가 아니라는 사실을 C가 알 수 있는 것은 C 자신이 3위일 때뿐이므로, 최종적으로 A-M2, B-M1, C-M3이 된다.
다음은 6월의 정답자로 선정된 조강진님의 해설입니다.



