8월의 퍼즐에 참여해주신 모든 분들께 감사드립니다!
8월의 퍼즐에 참여해주신 분 중 정답과 함께 좋은 풀이를 보내주신 김호진님께
HORIZON에서 준비한 선물을 전달드릴 예정입니다.
이 문제는 러시아에서 6학년과 7학년을 대상으로 개최되는 수학 축제Mathematical Festival에서 2011년에 출제된 문제로, 출제자는 알렉산데르 샤포발로프Alexander Shapovalov였다.
정답은 열다섯 개의 수가 나타나게 하는 것이 최선이며, 다음은 그 한 예이다. 이 배열에서는 5를 제외한 열다섯 개의 수가 모두 나타난다.

먼저 \(4\times4\) 배열에서 네 귀퉁이에 오는 수는 가로, 세로, 대각선 방향에서 가장 큰 스물두 개 수에 반드시 나타난다는 점에 주목한다. 되도록 많은 수가 나타나게 하려면, 네 귀퉁이에 작은 수를 배치해야 한다.
네 귀퉁이에 수를 배치하고 나면, 남은 열두 개의 수 가운데 가장 작은 수는 남은 자리 어디에 배치해도 가로, 세로, 대각선 방향 가운데 어딘가에 더 큰 수가 나타난다. 따라서 스물두 개 수에 1부터 16까지 열여섯 개가 모두 나타날 수는 없다.
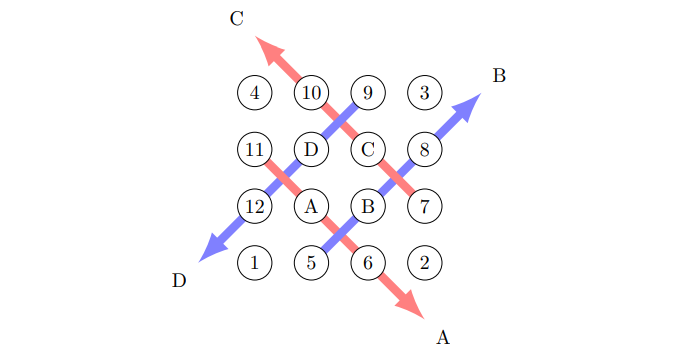
다음 그림처럼 네 귀퉁이에 1, 2, 3, 4를 배치하면, 5는 스물두 개 수에 나타날 수 없으므로, 6부터 16까지가 모두 나타날 수 있게 배치하는 것이 최선이다.

5를 가장 아래 줄에 배치하면 6이 나타날 수 있는 방법은 6을 1 바로 위에 두거나 5 오른쪽에 두어, 5와 6의 두 수만 비교하는 것뿐이다. 6을 5 오른쪽에 배치하자.

7이 나타나게 하려면 1 바로 위나 2 바로 위에 배치하는 방법뿐이다. 7을 2 바로 위에 두고 6을 배치한 것과 같은 방법으로 8을 배치하자.

나머지 네 수는 모두 12보다 큰 수들이므로, 남은 자리에 어떻게 배치하든 대각선 방향에서 네 수가 모두 선택될 수밖에 없다.
다음은 8월의 정답자로 선정된 김호진님의 해설입니다.
1부터 16까지 수를 \(4\times 4\)로 배열했을 때, 수 a가 가능한 22개의 선 위에 놓인 수들 중 최대값이 될 수 있는 경우 “a를 얻는다” 라고 하겠습니다.
첨부하는 그림과 같이 하면 5를 제외한 나머지 15개의 수를 얻을 수 있습니다. 따라서 16개의 수를 모두 얻을 수는 없음을 보이면 얻을 수 있는 수의 최대 갯수가 15임을 보이는 것입니다. 모든 수를 얻는 것은 불가능하다는 것을 아래에서 설명하겠습니다.
1을 얻기 위해서는, 네 귀퉁이 중 한 군데에 1을 적어야 합니다. 네 귀퉁이가 아닌 나머지 12 칸은, 그 칸을 포함하는 가로, 세로, 두 대각선 방향의 선에 항상 적어도 두개의 빈 칸이 있으므로, 네 귀퉁이가 아닌 곳에 1을 적으면 가장 작은 수인 1을 얻을 수 없습니다. 1을 네 귀퉁이 중에 한 군데에 적은 후에는 동일한 이유로 2를 남은 세 귀퉁이 중 한 군데에 적어야 합니다. 비슷하게 3, 4도 네 귀퉁이 중에 적어야 합니다. 그러므로 네 귀퉁이는 1, 2, 3, 4로 채워야 합니다.
이제 5에서 16까지 12개의 수를 네 귀퉁이를 제외한 12개의 칸에 적어야 합니다만, 남은 칸들을 포함하는 가로, 세로, 두 대각선 방향의 선에는 또다시 (이미 숫자가 적힌 네 귀퉁이를 제외하고도) 항상 적어도 두개의 빈칸이 있으므로, 남은 수 중에 가장 작은 5는 얻을 수 없습니다. (설명 끝)