12월의 퍼즐에 참여해주신 모든 분들께 감사드립니다!
12월의 퍼즐에 참여해주신 분 중 정답과 좋은 풀이를 보내주신 네 분을 선정했습니다.
문제1 정수현, 문제2 김종일, 문제3 장필훈, 문제4 이광현
이번 문제는 직접 수를 만들어 보는 수밖에 없다.
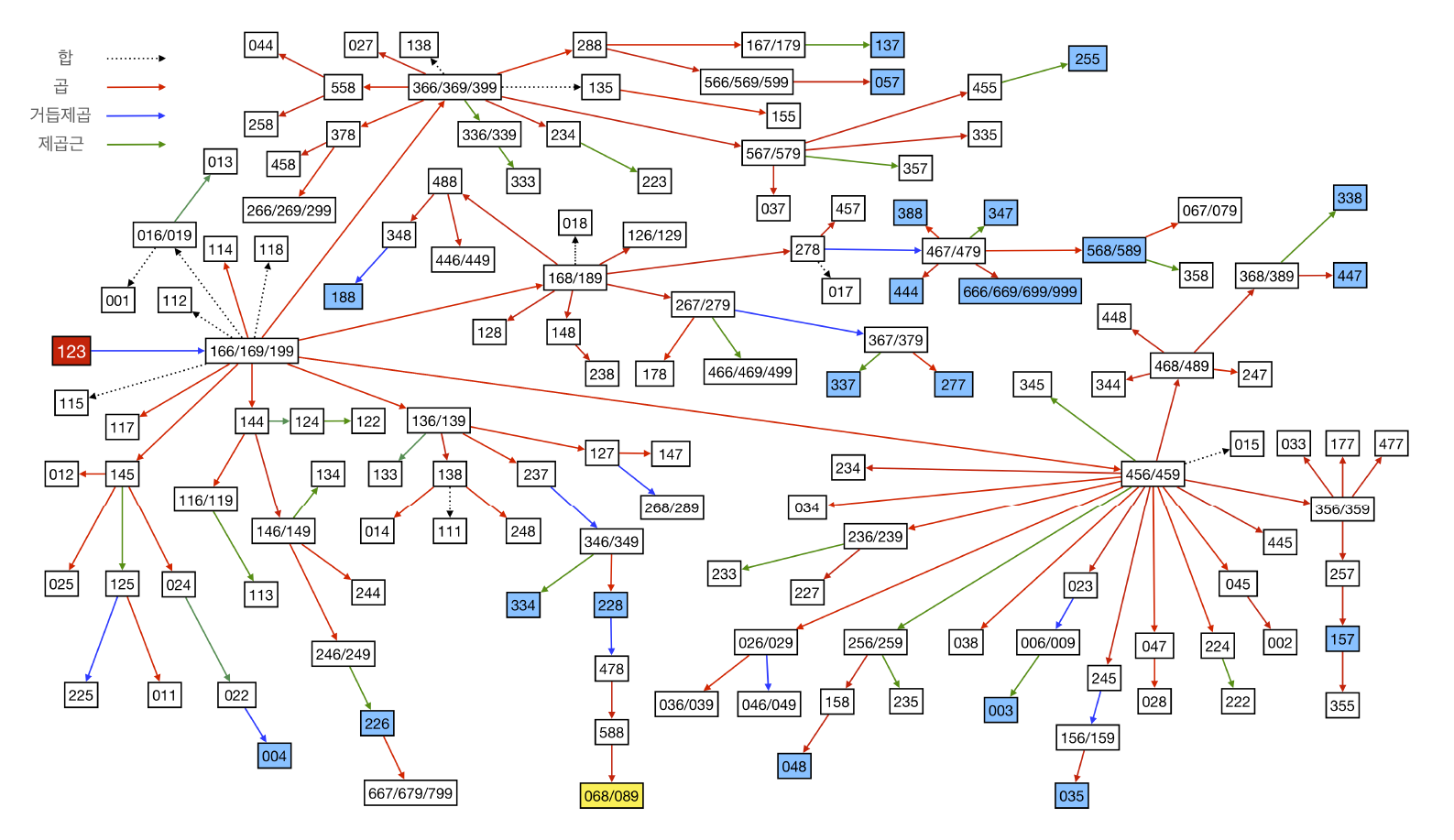
문제1은 오븐으로 구워낼 수 있는 가장 큰 수를 물었고, 그 답은 999이다. 아래의 그림은 1, 2, 3에서 출발하여 숫자 개수를 줄이지 않고 만들 수 있는 수들을 나열한 것이다. 이 과정에 따르면 1, 2, 3에서 출발하여 5단계만에 6, 6, 6을 만들 수 있고, 이를 배열하면 999가 된다.
999: \(1,2,3 \xrightarrow{13^2 = 169} 1,6,6 \xrightarrow{91 \times 9 = 819} 1,6,8 \xrightarrow{91 \times 8 = 728} 2,7,8 \\
\xrightarrow{8^2 = 64} 4,6,7 \xrightarrow{74 \times 9 = 666} 6,6,6 \xrightarrow{\text{배열}} 999\)
물론 이 과정은 유일하지 않다.
문제2는 오븐으로 구워낼 수 없는 가장 작은 수를 물었고, 그 답은 377이다. 두 자리 수를 모두 만들 수 있는 것은 직접 확인할 수 있고, 아래의 그림으로 376까지의 세 자리 수를 모두 만들 수 있음을 확인할 수 있다. 이 그림은 각 수가 만들어지는 단계를 나타낸 것으로, 원래는
\[
168 \xrightarrow{81 \times 6 = 486} 4,6,8 \xleftarrow{54 \times 9 = 486} 456
\]
처럼 두 가지 이상의 방법으로 만들 수 있는 것들을 하나씩으로 줄여서 간략하게 만들었다. 그림에서 파란 상자는 5단계를 뜻한다.
문제3은 가장 많은 단계가 필요한 수를 물었고, 그 답은 아래의 그림에서 노랗게 표시한 068/089로 모두 여덟 단계가 필요하다. 즉,
\[
608,680, 806,809,860,890, 908,980
\]
의 여덟 수는 8단계에서야 만들어진다.
문제 4는 경우의 수가 너무 많아 출제자도 정답을 모른다. 답을 올린 분 가운데 가장 많은 수를 찾은 분을 정답자로 선정하였다.
문제1 정수현님의 해설입니다.
123 169 166 136 139 127 289 268 368 389 278 467 479 666 999
13^2=169 9->6 6×6=36 6->9 3×9=27 17^2=289 9->6 6^2=36 6->9 3×9=27
8^2=64 6->9 74×9=666 6->9
문제2 김종일님의 해설입니다.
정답: 377
풀이: 1에서 999까지의 숫자 중 만들 수 없는 수는 모두 99개이다.
그 수들의 리스트는 아래와 같다.
377, 500, 505, 506, 508, 509, 550, 555, 556, 557,
559, 560, 565, 575, 577, 578, 580, 587, 590, 595,
605, 606, 609, 650, 655, 660, 668, 677, 678, 686,
687, 688, 689, 690, 698, 700, 707, 708, 737, 755,
757, 758, 767, 768, 770, 773, 775, 776, 777, 778,
779, 780, 785, 786, 787, 788, 789, 797, 798, 800,
805, 807, 808, 850, 857, 866, 867, 868, 869, 870,
875, 876, 877, 878, 879, 880, 886, 887, 888, 889,
896, 897, 898, 899, 905, 906, 909, 950, 955, 960,
968, 977, 978, 986, 987, 988, 989, 990, 998 (총 99개)
문제3 장필훈님의 해설입니다.
(프로그램으로 구현해서 돌려봤습니다)
문제3. 오븐을 가장 많이 써야 하는 수
608, 680, 806, 809, 860, 890, 908, 980 (모두 8번 필요)
문제4 이광현님의 해설입니다.
문제 3에서 처럼 자리수의 변화 없이 최대한 이어 나가게 하면 더 많은 수를 생성할 수 있습니다.
8단계 까지는 문제 3의 답과 동일합니다.
0단계)
>> 1, 2, 3, 12, 13, 21, 23, 31, 32, 123, 132, 213, 231, 312, 321 (15개)
1단계) 13^2 = 169
>> 6, 9, 16, 19, 61, 66, 69, 91, 96, 99, 166, 169, 196, 199, 616, 619, 661, 691, 916, 919, 961, 991 (22개)
2단계) 61*6 = 366
>> 36, 39, 63, 93, 366, 369, 396, 399, 636, 639, 663, 639, 936, 939, 963, 993 (16개)
3단계) 63*6 = 378
>> 7, 8, 37, 38, 73, 78, 83, 87, 378, 387, 738, 783, 837, 873 (14개)
4단계) 3*8 = 24 (7은 그대로)
>> 4, 24, 27, 42, 47, 72, 74, 247, 274, 427, 472, 724, 742 (13개)
5단계) 4*7 = 28 (2는 그대로)
>> 22, 28, 82, 228, 282, 822 (6개)
6단계) 28^2 = 784
>> 48, 78, 84, 478, 487, 748, 784, 847, 874 (9개)
7단계) 84*7 = 588
>> 5, 58, 85, 88, 588, 858, 885 (7개)
8단계) 85*8 = 680
>> 0, 60, 68, 80, 86, 89, 90, 98, 608, 680, 806, 809, 860, 890, 908, 980 (16개)
9단계) 60*8 = 480
>> 40, 408, 480, 804, 840 (5개)
10단계) 4 의 제곱근 = 2 (8,0 그대로)
>> 20, 208, 280, 802, 820 (5개)
11단계) 8^2 = 64 (0 그대로)
>> 46, 49, 64, 94, 406, 409, 460, 490, 604, 640, 904, 940 (12개)
12단계) 90*4 = 360
>> 30, 306, 309, 360, 390, 603, 630, 903, 930 (9개)
13단계) 90*3 = 270
>> 70, 207, 270, 702, 720 (5개)
14단계) 7^2 = 49 (0 그대로)
>> (추가 없음 11단계와 동일함)
15단계) 4 제곱근 = 2 (9 0 그대로)
>> 29, 92, 206, 209, 260, 290, 602, 620, 902, 920 (10개)
16단계) 9^2 = 81 (0 그대로)
>> 10, 18, 81, 108, 180, 801, 810 (7개)
17단계) 80-1 = 79
>> 79, 97 (2개)
>> (더이상 추가 없음)
15+22+16+14+13+6+9+7+16+5+5+12+9+5+10+7+2 => 총 173개의 수를 만들 수 있습니다.
(최적 해 여부는 확인 안되었습니다.)