완벽한 혼돈은 가능할까? 갑자기 이게 무슨 철학적인 질문인가 생각하는 독자들이 있을 것이다. 필자가 소개하고자 하는 램지 이론Ramsey theory은 이 철학적인 질문에 대한 답을 찾는 수학적인 시도이다.
필자는 가끔 로또 1등에 당첨되어서 유유히 삶을 만끽하는 모습을 상상하는 공상을 펼칠 때가 있다. 로또를 사본 적도 없으면서 이런 상상을 하게 되는걸 보면, 일확천금에 대한 환상이 있는 것 같다. 그런데 이런 환상을 가진 사람이 필자만은 아닌 듯하다. 일부의 사람들은 로또번호가 너무 작위적이라며 로또 추첨이 조작이 아니냐는 주장을 한다.
최근의 로또 당첨 번호를 두 개만 살펴보자.
\(940\text{회}: \overline{3}, 15, \underline{20}, \overline{\underline{22}}, \underline{24}, \overline{41}. \quad 941\text{회}: \overline{12}, \underline{14}, 25, \overline{\underline{27}}, \overline{39}, \underline{40}.\)
940회 당첨 번호에서는 밑줄 친 세 숫자 20, 22, 24가 등차수열을 이루고, 윗줄 친 세 숫자 3, 22, 41도 등차수열을 이룬다. 941회 번호에는 밑줄 친 세 숫자 14, 27, 40이 등차수열을 이루고, 윗줄 친 세 숫자 12, 27, 39는 12+27=39로 \(x+y=z\)라는 방정식을 만족한다. 이런 식의 패턴을 발견하고는 “어떻게 숫자가 이렇게 조화롭고 인위적일 수가 있지?”라고 생각하는 사람들이 로또 조작설을 믿게 되는 것 같다.
물론 필자는 로또 번호가 규칙 없이 무작위로 골라진 숫자라고 믿는다. (과연 진정한 무작위가 가능한가 하는 또 다른 철학적인 질문은 미뤄두자.) 하지만 이렇게 무규칙적으로 골라진 ‘혼돈’의 숫자에서도 뭔가 ‘질서’가 있어 보이는 부분구조가 있다는 것이 신기할 따름이다.
아마 심리학자나 뇌과학자들은 이런 현상을 보고 인간은 혼돈 속에서도 조화로운 형태나 규칙을 찾는 성향을 보인다고 흥미로워하며 인간의 심리나 두뇌를 연구할 것이다. 그러나 우리는 수학을 하는 사람이기에, 이런 현상을 보고 인간에 대해 고찰하는 대신 좀 더 본질적인 자연 그 자체에 대해서 연구할 것이다.
질문1. 과연 완벽한 혼돈은 가능한가?
위의 질문을 더 구체적으로 기술해보면 다음과 같다: “커다란 구조가 있으면, 그 구조가 아무리 무규칙하고 혼란스러워도, 그 안에서 질서 있는 부분을 항상 찾을 수 있을까?”
램지 이론이란?
이 질문이 바로 램지 이론의 출발점이다. 물론 우리가 어떤 구조를 생각하느냐에 따라, 그리고 어떤 부분을 질서 있다고 생각하느냐에 따라서 이 질문의 의미는 달라진다.
아주 간단한 구조인 집합을 생각해보자. 집합 내의 원소들은 어떠한 성질을 가지고 있다. 성질의 가짓수에 비해 집합이 크면 같은 성질을 가지는 원소를 여러 개 찾을 수 있다. 예를 들어, 로또 번호 6개의 숫자가 있으면 항상 짝수를 세 개 찾을 수 있거나 홀수를 세 개 찾을 수 있다. 길가는 사람 열세 명을 고르면 그중 같은 달에 태어난 사람 두 명을 항상 찾을 수 있다.
더 일반적으로, \(nk+1\)개 이상의 원소 각각이 \(k\)개 중 하나의 성질을 가지면, 같은 성질을 가지는 \(n+1\)개의 원소를 항상 찾을 수 있다는 원리를 ‘비둘기집의 원리’라고 부른다. 예를 들어, \(365=52\cdot 7+1\)이므로 윤년이 아닌 한해에는 53번 돌아오는 요일을 항상 찾을 수 있다. (2021년에는 금요일이 유일하게 53번 돌아온다.) 비둘기 집의 원리는 가장 기본적인 램지이론의 예이다.
좀 덜 간단한 구조인 자연수의 집합을 생각하면, 위에서와 같이 로또 번호의 예를 다시 생각해 볼 수 있다. 1에서 45까지의 숫자 중에 6개의 숫자를 고르면, 그 안에서 항상 길이 3짜리 등차수열을 찾을 수 있을까? 더 일반적으로 \(1\)에서 \(n\)까지의 숫자 중에 \(m\)개의 숫자를 고르면, 길이가 \(k\)인 등차수열을 항상 찾을 수 있을까? 1975년에 세메레디Endre Szemerédi는 다음의 정리를 증명해 이 질문에 답했다.
정리2 (세메레디Szemerédi, 1975). 주어진 자연수 \(k\)와 양의 실수 \(\varepsilon\)에 대해서, \(n\)이 충분히 크다면 다음이 성립한다: \(1\)에서 \(n\)까지의 숫자중에 \(\varepsilon n\)개 이상의 숫자를 고르면, 고른 숫자 안에서 항상 길이가 \(k\)인 등차수열을 찾을 수 있다.
이외에도 특정 집합에서 \(x+y=z\)의 등식을 만족하는 세 숫자를 찾을 수 있는가, 더 일반적으로 \(f(x_1,\dots, x_k)=0\)의 특정 방정식을 만족하는 숫자 \(x_1,\dots, x_k\)을 찾을 수 있는가 등에 관한 연구가 진행되고 있다.
자연수 집합 이외에도 우리가 생각 할 수 있는 재미있는 구조 중 하나는 그래프graph이다. 그래프는 집합에서의 이진 관계binary relation를 표현하는 수학적 구조이다. 주로 \(V\)라는 유한집합을 생각해 그 원소들을 꼭짓점vertex이라고 부르고, \(E =\{ \{u,v\} :u,v\in V\}\)라는 \(V\)의 원소들의 (순서가 없는) 쌍으로 이루어진 집합으로 생각해 그 원소들을 변edge이라고 부르며, 그래프는 꼭짓점 집합과 변 집합의 순서쌍 \((V,E)\)로 표현한다.
그래프 \(G=(V,E)\)에서 두 꼭짓점 \(u,v\) 사이에 변이 있으면, 즉 \(\{u,v\}\in E\)가 성립하면 우리는 두 꼭짓점 \(u,v\)가 연결되어 있거나 혹은 인접하였다고 한다. \(n\)개의 꼭짓점에서 모든 꼭짓점의 쌍이 서로 인접한 그래프를 \(n\)개의 꼭짓점을 가진 완전 그래프라고 부르고, \(K_n\)으로 표시한다.
그래프 구조에서 완벽한 혼돈이 가능한지에 대한 질문을 처음 던지고 답한 사람이 램지Ramsey이다. 아래 램지의 정리는 램지 이론에서의 최초의 정리로, 질문1에 대한 연구가 ‘램지 이론’이라는 이름으로 불리게 되는 계기가 되었다.
정리3 (램지Ramsey의 정리).주어진 자연수 \(t_1,\dots, t_s\)에 대해서 \(n_0=n_0(t_1,\dots, t_s)\)가 존재해서 모든 자연수 \(n\geq n_0\)가 다음의 성질을 만족한다: \(K_n\)의 모든 변을 \(\{1,\dots,s\}\) 중 하나의 색으로 칠하면, 어떤 방식으로 색칠을 하더라도 항상 \(i\in \{1,\dots, s\}\)가 존재해서 모든 변의 색깔이 \(i\)인 \(K_{t_i}\)를 찾을 수 있다.
즉, 아무리 혼돈스럽게 \(K_n\)의 변을 색칠하더라도, 모든 변의 색깔이 같은 부분그래프를 찾을 수 있다는 것이 램지의 정리이다. 모든 변의 색깔이 같은 \(K_t\)를 단색monochromatic \(K_t\)라고 부르자. 이런 사실을 알게 되면 자연스럽게 위의 숫자 \(n_0\)이 얼마나 커야 위의 정리가 성립하는지에 대한 질문을 하게 된다.
정의4. \(R(t_1,t_2,\dots, t_s)\)를 다음을 만족하는 최소의 \(n\)으로 두자: 완전 그래프 \(K_n\)의 각각의 변을 \(1,\dots,s\)의 색깔 중 하나로 색칠할 때, 어떻게 색칠을 하더라도 \(i\in \{1,\dots,s\}\)가 존재해서 모든 변이 \(i\)로 색칠된 단색 \(K_{t_i}\)를 찾을 수 있다.
예를 들어, \(R(3,3)\)의 값이 \(6\)임을 확인하는 것은 어렵지 않다. 이를 확인하기 위해서 \(R(3,3)\leq 6\)을 먼저 보이고, \(R(3,3)>5\)를 보이자.
\(R(3,3)\leq 6\)이라는 말은 완전그래프 \(K_6\)의 각각의 변을 빨강과 파랑의 두 가지 색깔을 이용해 어떠한 방식으로 색칠한다고 해도, 항상 빨간 \(K_3\)나 파란 \(K_3\)을 찾을 수 있다는 말이다. 이를 증명하는 것은 간단하다. \(K_6\)의 변이 임의의 방식으로 색칠이 되어 있다고 하고, 여기서 꼭짓점 하나를 골라 \(v\)라고 부르자. ([그림2])
비둘기 집의 원리the pigeonhole principle에 의해서 연결된 다섯 개의 변 중에 적어도 세 개는 같은 색이다. 편의상 이 색을 빨간색이라고 하고, 세 변의 다른 쪽 끝 꼭짓점을 \(u_1,u_2,u_3\)라고 부르자. 세 꼭짓점 \(u_1,u_2,u_3\) 사이에 있는 변 중에 하나라도 빨간색으로 색칠되어있다면 그 두 꼭짓점과 \(v\)를 잡으면 빨간 단색 \(K_3\)를 얻고 만약 셋 모두 파란색으로 색칠되어있다면 꼭짓점이 \(u_1,u_2,u_3\)로 이루어진 파란 단색 \(K_3\)를 얻는다. 따라서 어떠한 경우라도 우리는 단색 \(K_3\)를 찾을 수 있다.
또한 \(R(3,3)>5\)라는 식의 뜻은 완전 그래프 \(K_5\)의 선을 빨강과 파랑으로 잘 칠하면, 빨간 \(K_3\)와 파란 \(K_3\)가 모두 존재하지 않도록 할 수 있다는 말이다. 예를 들어 위의 [그림3]과 같이 색칠하면 우리가 빨간 삼각형과 파란 삼각형을 모두 피하는 것이 가능하다.
아래에서 우리는 주로 \(t_1=\dots = t_s\)인 대칭적인 경우를 다룰 것이기 때문에 간단하게 \(R(t;s)=R(\overbrace{t,\dots, t}^\text{\(s\)개})\)라는 표기법을 사용하도록 하자. 즉, 우리는 방금 \(R(3;2)\)\(=R(3,3)=6\)이라는 사실을 배웠다.
우리가 정의한 이 숫자를 램지 수Ramsey number라고 부르는데, 이는 혼돈 속에서 얼마나 큰 질서를 찾을 수 있는지를 정량적으로 표현하는 숫자이다. 즉, 크기 \(t\)짜리 질서 있는 부분을 찾기 위해 필요한 \(K_n\)의 크기인 램지 수가 작다는 것은, 그리 크지 않은 혼란스러운 구조 안에서 크기 \(t\)짜리 질서 있는 구조를 항상 찾을 수 있다는 말이다. 관점을 바꾸어 말하면, 램지 수가 작다면 전체 구조의 크기에 비해서 상대적으로 큰 질서 있는 부분을 항상 찾을 수 있고, 반대로 램지 수가 크다면 작은 질서 있는 부분이 전혀 존재하지 않는 커다란 혼란스러운 구조가 존재한다.
그런데 램지 수를 아는 것이 왜 중요할까? 이 램지 수는 정보이론information theory, 전산학computer science, 정수론number theory, 논리학logic, 기하geometry, 위상수학topology 등 많은 분야에 활용된다. 이제 정보이론에서 램지 이론의 간단한 활용 하나를 살펴보자.
램지 이론 활용의 예
다른 사람과 통신을 한다고 생각해보자. 우리의 소통 방법은 특정 기호를 나열해 메시지를 전달하는 것이다. 기호는 문자일 수도 있고, 몸짓일 수도 있고, 색깔일 수도, 소리의 높낮이일 수도 있다. 그런데 이 ‘기호’들에는 불분명함이 존재한다. \(a\)와 \(u\) 같이 손글씨의 모양이 비슷해서 헷갈릴 수 있고, \(bad\)와 \(bed\)처럼 발음이 비슷해서 헷갈릴 수도 있다. 장거리 통신에서는 \(000110\)이라는 메시지에 잡음이 섞여 \(100110\)과 혼란을 줄 수도 있다.
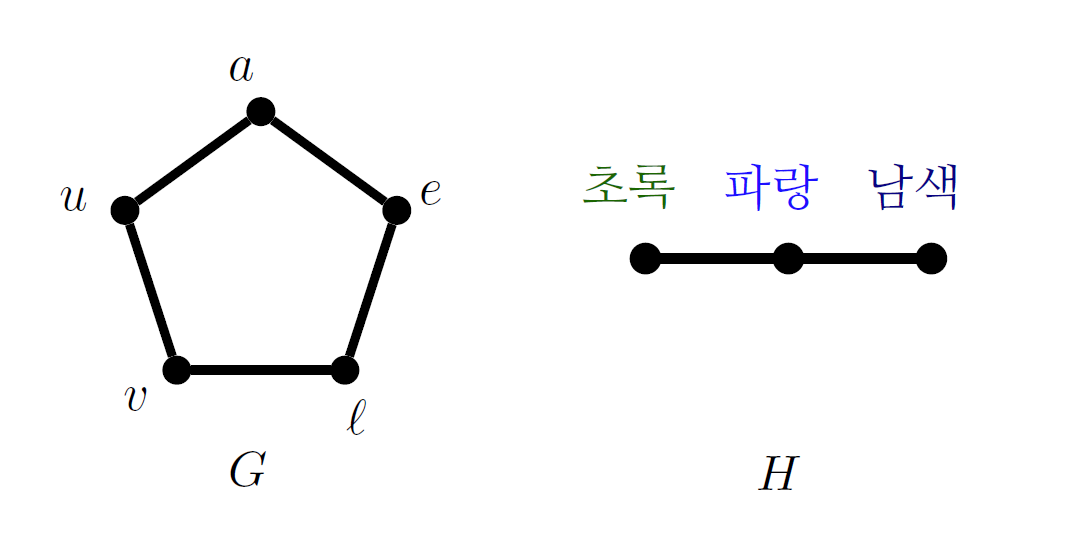
우리가 소통에서 사용하는 특정 기호들을 꼭짓점으로 두고, 서로 혼란의 여지가 있는 두 기호를 변으로 연결하자. 예를 들어, \(a\)와 \(u\)는 손글씨가 비슷해서 헷갈릴 수 있으니 둘 사이에 변을 그리고, \(e\)와 \(a\)는 발음이 비슷하여 헷갈릴 수 있으니 변을 그린다. 이런 식으로 하면 [그림4]와 같은 혼란 그래프confusion graph를 얻는다.
위와 같은 혼란을 피하기 위해서는, 위의 혼란 그래프에서 독립집합independent set을 골라 그 집합에 있는 기호만을 사용해 소통하면 된다. 독립집합은 꼭짓점들의 집합으로, 그 집합 안의 꼭짓점들이 서로 연결되어있지 않은 집합을 말한다. 예를 들어 위에서 \(\{a,v\}\)는 독립집합이고, \(\{a,u,\ell\}\)은 \(a\)와 \(u\)가 연결되어 있지 않으니 독립집합이 아니다. 즉, \(a,v\)의 두 기호를 사용해 통신을 하면 혼란의 여지가 없지만, \(a,u,\ell\)의 세 기호로 통신을 하면 혼란의 여지가 커진다. 특정 그래프 \(G\)의 가장 큰 독립집합의 크기를 \(\alpha(G)\)로 적고 독립수independence number라고 부른다.
또한 한 가지 이상의 기호를 동시에 써서 소통하는 경우가 있다. 알파벳과 함께 색깔도 소통에 사용한다고 생각해보자. 초록색, 파란색, 남색의 세 가지 색깔 간의 혼란 그래프를 [그림4]처럼 생각해보자. 초록색과 파란색은 헷갈릴 수가 있고, 남색과 파란색도 헷갈릴 수 있다고 하자.
이때 두 그래프 \(G,H\)의 강한 곱strong product \(G\boxtimes H\)를 다음과 같이 정의하자. (\(a\),초록), (\(a\),파랑), \(\dots\), (\(e\),남색)의 15개 꼭짓점을 정의하고, 두 꼭짓점이 서로 헷갈릴 여지가 있으면 둘 사이에 변을 넣는다.
예를 들어, 초록색 \(a\)와 파란색 \(a\)는 혼동의 여지가 있으니 연결한다. 초록색 \(a\)와 초록색 \(u\)도 혼동의 여지가 있으니 연결한다. 그리고 초록색 \(a\)와 파란색 \(u\)도 손글씨·색깔을 동시에 헷갈릴 여지가 있으므로 연결한다. 하지만 초록색 \(a\)와 초록색 \(v\)는 손글씨에서 혼동의 여지가 없고, 초록색 \(a\)와 남색 \(a\)도 색깔에서 혼동의 여지가 없으니 연결하지 않는다. 즉, 두 성분 각각 모두 ‘같거나 혼동의 여지가 있으면’ 연결해 강한곱 \(G\boxtimes H\)를 얻는다.
이런 식의 그래프의 강한 곱에서 특정 독립집합을 찾는 일은 여러 가지 요소들을 복합적으로 사용하면서 혼란의 여지가 없고 효율적인 통신을 위한 프로토콜을 만드는 일에 이용할 수 있다. 그래서 이런 그래프의 독립수의 크기를 대략적으로라도 알아내는 일은 유용한데, 독립수의 계산에 램지이론이 사용될 수 있다. 예를 들어, 1966년에 헤들린Eric Hedlin은 그래프의 강한 곱의 독립수를 램지 수를 이용해서 계산하는 다음의 식을 찾아냈다:
\((\alpha(G\boxtimes H) \leq R(\alpha(G)+1, \alpha(H)+1)-1.\)
즉, 우리가 램지 수가 얼마나 큰지 계산할 수 있다면, 그래프의 강한 곱의 독립수를 계산하는 데 도움이 된다. 그렇다면 램지 수의 크기는 얼마나 정확하게 알려져 있을까?
램지 수의 상한
먼저 램지 수의 상한부터 살펴보자. 가장 간단한 방식으로 상한을 구하려면 다음의 점화 부등식을 생각할 수 있다.
\(R(t_1,\dots, t_s) \leq \sum_{i=1}^{s} \left( R(t_1,\dots,t_{i-1}, t_i -1, t_{i+1},\dots, t_s) – 1 \right) +1.\)
이 점화 부등식은 앞서 \(R(3,3)\leq 6\)을 증명한 논리를 수학적 귀납법과 함께 사용해 간단하게 증명할 수 있다. \(s\)개의 색깔을 \(1,\dots, s\)의 숫자로 표현하자. \(n\)을 다음과 같이 두자.
\(n= \sum_{i=1}^{s} \left(R(t_1,\dots,t_{i-1}, t_i -1, t_{i+1},\dots, t_s)-1\right) +1\)
그리고 \(n\)개의 꼭짓점이 있는 완전그래프의 변을 \(s\)개의 색으로 색칠했다고 가정하고, 특정 꼭짓점 \(v\)을 포함하는 모든 변을 생각해보자. 비둘기 집의 원리에 의해서 어떤 \(i\in \{1,\dots, s\}\)가 존재해서 \(v\)를 포함하는 변 중에 적어도 \(R(t_1,\dots,t_i -1,\dots, t_s)\)개가 모두 \(i\)로 색칠되어 있다. 이 변의 다른 쪽 끝 꼭짓점들을 모으면 적어도 \(R(t_1,\dots,t_i -1,\dots, t_s)\)개의 꼭짓점을 모을 수 있다. 이 꼭짓점들이 다시 더 작은 완전그래프를 이루므로, 귀납적 가정에 의해서 우리는 이 안에서 모든 선이 \(j\)로 칠해진 \(K_{t_j}\)를 찾거나 모든 선이 \(i\)로 칠해진 \(K_{t_{i}-1}\)을 찾을 수 있다.
전자의 경우에는 우리가 원하는 \(j\)로 색칠된 단색 \(K_{t_j}\)를 찾았고, 후자의 경우에는 \(i\)로 색칠된 단색 \(K_{t_i-1}\)과 \(v\)를 함께 잡으면 우리가 원하는 단색 \(K_{t_i}\)가 된다.([그림4]) 이와 같은 증명 방식을 근방 따라가기neighborhood chasing라고 부른다. 위의 점화식을 이용하면 \(R(t;2) \leq 4^t\)임을 어렵지 않게 보일 수 있다.
\(R(t;2)\)에 관한 알려진 가장 좋은 상한은 위의 상한에서 그리 많이 발전되지 않았다. 콘론David Conlon은 2009년에 근방 따라가기 증명법과 유사 무작위성pseudorandomness을 이용해서 \(R(t;2) \leq 4^{t – \frac{C(\log{t})^2}{\log\log t} }\)를 만족하는 상수 \(C>0\)가 존재함을 보였고, 2020년에 MIT의 학부생 샤Ashwin Sah는 콘론Conlon의 방법을 발전 시켜 \(R(t;2) \leq 4^{t- C(\log{t})^2}\)를 만족하는 상수 \(C\)가 존재함을 보였다. 이는 매우 큰 발전이지만, 기본적인 증명으로 얻을 수 있는 상한인 \(4^t\)보다 비지수적sub-exponential 발전을 이루는 데 그쳤다. 즉, 우리는 충분히 큰 \(t\)에 대해서 \(R(t;2)\)가 \(3.99^t\)보다 작은지 아닌지도 아직 알지 못한다.
램지 수의 하한
그렇다면 램지 수의 하한은 어떨까? 어떤 숫자 \(n\)에 대해서 램지 수의 하한 \(R(t;s)\geq n\)을 증명하기 위해서는 우리가 직접 완전 그래프 \(K_n\)의 변을 \(s\)개의 색으로 잘 칠하여 단색 \(K_t\)가 존재하지 않음을 확인하면 된다. 언뜻 생각하기에는 하한을 보이는 것이 상한을 보이는 것보다 쉽다고 생각할 수 있지만, 오히려 이런 직관과는 다르게 하한의 증명이 상한보다 더 어렵다고 보는 사람이 많다.
모든 색칠 방법에 대해 단색 \(K_t\)를 찾을 수 있음을 보여야 하는 상한의 증명과 달리, 한 가지 색칠방법만 찾으면 하한이 증명되는데 왜 하한의 증명이 더 어려운 걸까? 더 나은 하한의 증명을 위한 여러 가지 시도가 있었지만 여러 명시적인explicit 색칠법은 모두 \(t\)에 대한 지수함수의 하한을 증명하지 못했다. 여기서 명시적이란, 우리의 색칠 방법이 어떠한지 명확하게 알려주는 증명법을 말한다.
프랑클-윌슨Frankl-Wilson, 노가Noga Alon, 바락-라오-샬 티엘-위그더슨Barak-Rao-Shaltiel-Wigderson, 코언Paul Cohen, 차토파디아야-주커만Chattopadhyay-Zukerman 등의 연구자들이 명시적 하한을 발전시켰고, 현재 우리가 아는 가장 좋은 명시적 하한은 어떤 1보다 작은 상수 \(\epsilon>0\)에 대해서 \(R(t;2)\geq 2^{2^{(\log\log t)^\varepsilon}}\)가 성립한다는 것이다. 하지만 이는 \(t\)에 관한 지수함수보다 훨씬 작고, 우리가 아는 상한 \(4^t\)와의 차이가 크다.
이렇게 명시적인 색칠 방법을 찾는 것은 매우 어렵지만, 다음의 확률적 방법론을 이용한 비명시적인 지수함수의 하한은 이미 1940년대에 증명되었다.
정리5(에르되시Erdős, 1947). \(R(t;2) \geq \frac{t 2^t}{\sqrt{2}e}.\)
이 하한의 증명은 매우 기발한 동시에 간단하다. \(n=\lfloor\frac{t 2^t}{\sqrt{2}e}\rfloor\)에 대해서 \(K_{n}\)의 각각의 변을 생각한다. 각 변에 대해서 독립적independent으로 공정한 동전fair coin을 던져서, 앞면이 나오면 변을 빨간색으로 색칠하고, 뒷면이 나오면 파란색으로 색칠한다. 그리고 그 결과로 나오는 색칠법이 단색 \(K_t\)를 가지지 않을 확률을 계산한다. \(K_t\)의 변의 개수가 \(\binom{t}{2}\)이고, 하나의 \(K_t\)가 단색으로 칠해지는 방법은 빨간색, 파란색의 두 가지이므로 특정한 \(t\)개의 꼭짓점 집합이 단색 \(K_t\)가 될 확률은 \(2\cdot 2^{-\binom{t}{2}}= 2^{1-\binom{t}{2}}\)이다.
한편 \(K_n\)안에는 \(\binom{n}{t}\)개의 서로 다른 \(t\)개의 꼭짓점 집합이 존재한다. 따라서 확률의 합에 관한 부등식the union bound을 쓰면, 적어도 하나의 단색 \(K_t\)가 존재할 확률은 \(\binom{n}{t} 2^{1-\binom{t}{2}}\)보다 작거나 같은데, 계산해보면 우리가 고른 \(n\)에 대해서 이 값은 \(1\)보다 작다. 따라서 동전을 이용해서 무작위로 색칠을 하면, 양의 확률로 우리가 원하는 색칠법을 얻을 수 있다. 이로부터 우리가 원하는 색칠법이 존재한다는 결론을 얻고, 따라서 \(R(t;2)>n\)라는 램지 수의 하한을 얻는다.
이와 같은 증명을 3개의 색깔에 대해 같은 방식으로 적용하면 \(R(t;3) \geq 3^{t/3}\)의 부등식을 얻을 수 있고, 여기에
\begin{align}
\tag{1}
R(t;s_1+s_2) \geq (R(t;s_1)-1)(R(t;s_2)-1)+1
\end{align}
이라는 알려진 관계식을 이용하면 다음의 하한을 얻는다.
\begin{align}
\tag{2}
R(t;3s)> 3^{st/2}, \quad R(t;3s+1)> 2^t 3^{(s-1)t/2} \quad \text{그리고} \quad R(t;3s+2)> 2^{t/2}3^{st/2}.
\end{align}
이런 확률론적 증명법은 존재성을 증명할 때 매우 유용하지만, 우리가 원하는 색칠법에 대한 정보를 전혀 주지 못한다는 단점이 있다. 이 증명이 나온 지 70년이 넘었지만, 현재 우리가 아는 가장 좋은 하한은 로바스Lovász의 국소정리Lovász local lemma를 이용해서 얻는 \(R(t;2) \geq (1-o(1))\frac{\sqrt{2}k 2^k}{e}\)이다. 이는 위에서 설명한 에르되시Erdős의 하한보다 약 2배 더 큰 숫자에 그치는 하한이다.
사용하는 색깔의 숫자가 3개 이상인 경우 또한 위에서 기술한 하한(2)을 지난 70년간 아무도 더 발전시키지 못했다. 그러다 최근에 콘론Conlon과 퍼버Asaf Ferber가 다음을 증명해 이 하한을 더 발전시켰다.
정리6. \(R(t;3) > 2^{7t/8+o(t)}\)이고 \(R(t;4)> 2^{t/2} 3^{3t/8+o(t)}\)이다.
이와 함께 (1)의 관계식을 이용하면 다음의 하한을 얻는다.
\begin{align}\label{lower bound 2}
R(t;3s)> 2^{\frac{7st}{8}+o(t)}, \enspace R(t;3s+1)> 2^{\frac{7(s-1)t}{8} +\frac{t}{2}}3^{\frac{3t}{8}+o(t)}, \enspace R(t;3s+2)> 2^{\frac{7st}{8}+\frac{t}{2}+o(t)}.
\end{align}
이후 위그더슨Wigderson이 콘런Conlon과 퍼버Ferber의 증명을 개량해서 \(t\geq 4\)인 경우에 \(R(t;s) \geq 2^{ (3s/8-1/4)(t/4-o(t))}\)의 하한을 증명했다. 에르되시Erdős의 증명처럼 콘런Conlon과 퍼버Ferber의 증명도 매우 간단해서, 전체 증명이 1.5페이지에 불과하다.
명시적인 하한을 주는 결정론적인deterministic 증명이 힘든 이유는, 여러 색깔의 단색 \(K_t\)들을 동시에 피하기가 어렵다는 데 있다. 빨강과 파랑 두 가지 색으로 변을 색칠할 때, 빨간색 \(K_t\)를 피하려고 노력하다 보면 파란색 \(K_t\)를 마주하게 되고야 만다. 빨간색으로 칠해지지 않은 모든 변은 파란색으로 칠해져야 하기에 생기는 문제이다.
하지만 색깔이 셋 이상이라면 이야기가 달라진다. 빨간색, 파란색, 초록색의 세 가지 색깔을 쓴다고 생각해보면, 빨간색 \(K_t\)를 피하는 명시적인 방법으로 그래프의 일부 변을 색칠할 때, 아직 색칠되지 않은 변은 파란색이 될지 초록색이 될지 결정되어 있지 않다. 따라서 빨간색을 결정론적으로 색칠하는 동안 아무런 문제가 생기지 않는다. 이런 식으로 빨간색 색칠을 결정론적으로 마친 뒤에 나머지 색칠되지 않은 변을 확률론적으로 무작위로 색칠한다. 이 결과로 얻는 색칠이 우리가 원하는 단색 \(K_t\)를 모두 피하는 색칠일 확률이 양수임을 보일 수 있다면, 우리는 더 발전된 하한을 보일 수 있다.
콘런Conlon과 퍼버Ferber의 증명을 간략히 설명해보자. 숫자 \(t\)가 주어져 있을 때, 벡터공간vector space \(\mathbb{F}_2^{t-1}\)에서 \(v\cdot v=0~({\rm mod}~2)\)를 만족하는 자가직교 벡터self-orthogonal vector \(v\)를 모아 놓은 집합을 \(V\)로 두자. 그리고 \(V\)를 꼭짓점으로 가지는 완전그래프 \(G\)를 생각하자. 이때 \(V\)는 \(t-2\)차원 벡터공간이다.
즉, \(G\)는 짝수개의 \(1\)을 성분component으로 가지는 \(0,1\)-벡터를 꼭짓점으로 가지는 그래프이다. 그래프 \(G\)의 변을 색칠하는데, \(u\cdot v = 1~({\rm mod}~2)\)를 만족하는 쌍 \(u,v\)에 대해서 변 \(\{u,v\} \in E(G)\)는 빨간색으로 색칠하고, 그 외의 모든 변은 확률 \(1/2\)으로 파란색 혹은 초록색으로 독립적으로 무작위로 색칠한다.([그림5]) 이때, 결정론적으로 색칠한 빨간색에서는 단색 \(K_t\)를 찾을 수 없다는 것을 다음과 같이 증명할 수 있다.
만약 빨간색 \(K_p\)가 있다면, 벡터 \(v_1,\dots, v_p\)가 있어서 \(v_i\cdot v_j = 1 ~({\rm mod}~2)\)이 성립한다. 숫자 \(p\)와 \(p-1\)중에 짝수를 \(s\)로 두면, \(v_1,\dots, v_s\)의 벡터는 선형 독립linearly independent임을 다음과 같이 보일 수 있다. 만약 어떤 \(\alpha_1,\dots, \alpha_s \in \mathbb{F}_2\)에 대해서 \(\sum_{j=1}^{s} \alpha_j v_j =\vec{0}\)이라면, 각각의 \(i\in \{1,\dots, s\}\)에 대해서
\(0 = v_i\cdot \vec{0}= v_i\cdot (\sum_{j=1}^{s} \alpha_j v_j) = \sum_{j=1}^{s} \alpha_j v_i\cdot v_j = (\sum_{j=1}^{s} \alpha_j)- \alpha_i\)
을 얻을 수 있다. 이 식이 모든 \(i\)에 대해서 참이므로 \(\alpha_1=\dots=\alpha_s\)여야만 한다. 만약 \(\alpha_1=\dots=\alpha_s=1\)이면 \(s\)가 홀수여야 \((\sum_{j=1}^{s} \alpha_j)- \alpha_i=0\)을 얻을 수 있는데 \(s\)가 짝수라서 모순이다. 따라서 \(\alpha_1=\dots = \alpha_s=0\)이 되고, 벡터 \(v_1,\dots, v_s\)는 선형독립이다. 따라서 \(s\leq dim(V) = t-2\)를 얻는데, \(s\)가 \(p,p-1\) 중에 고른 숫자라 \(p-1\leq t-2\)를 얻어 \(p\leq t-1\)이 된다. 따라서 위의 색칠에서는 빨간색 \(K_t\)가 없음을 알 수 있다.
이렇듯 결정론적인 색칠 방법으로 빨간 단색 \(K_t\)를 피하는 색칠을 한 후, 색칠이 안 된 변을 나머지 두 색깔로 무작위로 색칠하면, 파란색과 초록색 단색 \(K_t\)가 많지 않은 색칠법을 찾을 수 있다. 그리고 마지막으로 꼭짓점을 적당히 지움으로써 파란색과 초록색 단색 \(K_t\)를 완전히 없애 우리가 원하는 색칠법과 램지 수의 하한을 얻을 수 있다.
이 증명은 알고 나면 정말 자연스럽고 간단해 보이는데 지난 70여 년간 아무도 생각해 내지 못한 증명이다. 이렇듯 우리가 알고 있는 그래프 램지 수의 하한에 대한 증명은 모두 매우 간단하고 자연스럽다. 하지만 하한과 상한 사이의 간격은 매우 크고, 그 간격을 쉽게 줄일 수 있을 것으로 보이지 않는다. 그만큼 상하한을 발전시킬 창의적인 아이디어를 내기가 어렵다는 방증이다.
과연 우리가 아는 램지 수의 상한과 하한 중에 어느 쪽이 더 정답에 가까울까? 그리고 어떤 기발하고 자연스러운 증명이 상하한을 발전시킬 수 있을까? 이렇게 간단하고 자연스럽지만 매우 아름다운 증명을 볼 때면 수학의 아름다움에 매료되어 기쁘고 들뜨게 된다. 앞으로 누가 또 어떤 아름다운 증명을 발견해 우리를 즐겁게 해줄지 정말로 기대된다.