수학계의 노벨상이라고 할 수 있는 아벨상의 2021년 시상식이 5월 25일 한국시간으로 밤 10시에 온라인에서 개최되었습니다. 2021년 아벨상 수상자는 헝가리의 로바스 라슬로1Lovász László와 미국의 아비 위그더슨Avi Wigderson으로 결정되었습니다. 아벨상 홈페이지에서는 두 분의 수상 이유를 현대 수학의 중심 분야인 이산수학 및 이론컴퓨터과학의 토대를 만들고 선도적인 역할을 한 것으로 꼽았습니다. 그래프이론 전공자라면 모를 수 없는 로바스가 아벨상 수상자로 선정되었다는 소식을 듣고 두 가지 생각이 떠올랐습니다. 첫 번째는 당연히 받고도 남을 대가가 선정되었다는 것이었고, 두 번째는 로바스 라슬로의 수많은 업적 중에 어떤 업적을 대표로 뽑았을까 하는 것이었습니다.
끊임없이 좋은 문제를 제시하고 수많은 사람들과 교류하며 공동 연구를 한 것으로 유명한 수학자 에르되시 폴Erdős Paul의 영향으로 이산수학 분야에서 훌륭한 수학자들이 헝가리에 많습니다. 2003년 첫 아벨상이 수여된 이후, 헝가리 수학자가 수상자로 선정된 것은 2012년 세머레디 엔드레Szemerédi Endre에 이어 이번이 두 번째입니다. 세머레디도 이산수학 및 이론컴퓨터과학 분야의 기여로 아벨상을 수상하였습니다.
걸어온 길
세레메디가 의대에 입학했다가 반년 만에 자퇴한 뒤 공장에서 일하던 중 22살 때 수학과로 대학 진학을 하여 수학자의 길을 걷기 시작한 것과 달리, 1948년생인 로바스는 일찍부터 수학 영재였습니다. 헝가리 부다페스트의 파제카스 미하리Fazekas Mihály 고등학교에는 수학영재 특별반이 있는데, 로바스는 특별반이 생긴 첫해에 입학한 학생이었습니다. 같은 반에서 현재의 배우자를 만나 결혼하였는데, 그분 역시 이산수학 분야로 박사학위를 받았고 로바스와 여러 권의 책을 함께 썼습니다.
로바스는 1963년부터 국제수학올림피아드에 네 번 나가서 은메달 한 번과 금메달 세 번을 수상하였는데, 마지막 두 번은 만점이었습니다. 또한 그 당시 헝가리 TV에서 수학 영재들이 실력을 겨루는 프로그램이 있었는데 거기서 우승을 하기도 하였습니다. 잠깐 당시 일화를 소개하면, 방송은 서로 소리를 들을 수 없는 유리장 안에서 같은 문제를 받아 3분간 생각하고 해결하는 식으로 진행되었는데, 생방송으로 전국에 중계되는 인기 프로그램이었다고 합니다. 그때 최후의 2인만 남은 결승에서 로바스가 만난 친구는 고등학교 같은 반이었던 포사Pósa Lajor라는 친구였습니다. 로바스가 결승에서 포사보다 먼저 문제를 풀자 진행자가 어떻게 풀었는지 물어보니, 로바스는 사실 포사가 전에 알려준 문제와 비슷해서 빨리 풀 수 있었다고 대답했다고 합니다. 수학 영재였던 포사는 초등학생 때 주변의 소개로 에르되시와 만나기 시작하였는데 13살 때 에르되시와 첫 공저 논문을 출판하였습니다.
로바스는 포사의 소개로 고등학생이던 1963년 에르되시를 처음 만났습니다. 그 후 “헝가리 스타일의 이산수학” 분야 연구를 하여 고등학생 때 이미 여러 논문을 출판하였습니다. 고등학교를 졸업한 후 부다페스트에 위치한 외트뵈시 로란드 대학Eötvös Loránd University를 다니기 시작했는데 22살이 되던 1970년에는 이미 15개의 논문을 출판하였고 여러 국제 학회에서 발표를 하였습니다.
우리나라에서는 박사학위가 가장 높은 학위인 것과 달리, 당시 헝가리에는 4가지 종류의 학위가 있었습니다. 대학교에서 5년 공부하면 디플롬diplom을 받는데 석사 학위와 비슷합니다. 그리고 대학교에서 받는 박사doctor 학위는 다른 나라의 박사학위보다 조금 낮고, 헝가리과학한림원에서 받는 후보candidate 학위는 다른 나라의 박사학위보다 높으며, 헝가리과학한림원의 박사학위가 가장 높은 학위입니다.
특이하게도 대학교와 헝가리과학한림원이 독립적으로 학위를 주는데, 헝가리과학한림원의 후보 학위는 심사가 까다롭기 때문에 대학교의 박사 학위 받은 후에 몇 년이 지나서 받는 것이 보통이었습니다. 하지만 로바스의 경우 1970년에 헝가리과학한림원의 후보 학위를 먼저 받고 1971년에 대학교의 박사 학위를 받았습니다. 대학교의 경우 디플롬부터 받아야 해서 박사 학위를 받는데 시간이 더 걸렸지만, 헝가리과학한림원의 경우 그런 예외적인 상황이 있을 것이라고 생각하지 못하여 제한하는 규정이 없었다고 합니다. 그래서 로바스는 대학교 4년차 때 후보 학위 디펜스를 할 수 있었으며, 생각하지 못한 상황에 행정직원이 골머리를 앓았다고 합니다.
그 후 로바스는 1977년 헝가리과학한림원에서 박사 학위를 받았고, 1979년에는 헝가리과학한림원 최연소 회원이 되었습니다. 로바스는 조셉 아틸라 대학 교수로 있다가 1983년에 외트뵈시 로란드 대학교 교수로 옮겼고, 1993년 헝가리를 떠나 미국 예일대 교수가 되었으며, 1999년에는 학계를 떠나 미국 시애틀 근교에 있는 마이크로소프트 연구소의 이론그룹에서 수석연구원이 되었습니다.
미국 마이크로소프트 연구소에서 10여 년을 일하다가 아들이 고등학생이 될 즈음인 2006년 헝가리 외트뵈시 로란드 대학교로 돌아갔습니다. 이때 아들은 아버지가 다닌 고등학교를 다니면서 2007년부터 국제수학올림피아드에 2번 출전하여 은메달과 금메달을 받았습니다. 아버지와 아들이 국제수학올림피아드에서 금메달 4개를 받은 진기록은 앞으로도 쉽게 깨기 어려울 것입니다. 아들 또한 MIT에서 이산수학 분야 연구로 박사학위를 받았습니다. (특이하게도 이번 아벨상 수상자인 위거더슨의 아들도 현재 스탠퍼드대학 수학과에서 이산수학 분야 전공으로 박사과정을 밟는 중입니다.) 헝가리 전통에 따라 아버지의 이름을 물려받았기 때문에 우리 분야 수학자들은 중간 이름으로 아버지인지 아들인지 구분하고 있습니다.
최근 로바스는 연구뿐만 아니라 연구자들을 대표하는 활동도 하였습니다. 2007년부터 2010년까지 국제수학연맹 회장을 지냈으며, 2014년 세계수학자대회가 서울에서 개최되는 것으로 결정될 때 국제수학연맹 회장 자격으로 한국에 실사 방문을 하기도 하고 2009년 4월 서울이 단일 개최후보지로 결정되었음을 알려주기도 했던 분입니다. 그 후 2014년부터 2020년까지는 헝가리과학한림원 원장을 지냈습니다.
로바스는 2011년 사이먼스 재단과의 인터뷰에서 과거 물리학과 해석학이 함께 발전한 것처럼 수학과 그 응용 분야가 완전히 함께 발전하는 시기, 즉 이산수학과 이론컴퓨터과학이 함께 발전하는 시기를 경험할 수 있어서 매우 운이 좋았다고 말하였습니다. 응용과 무관하게 순수한 학문적 호기심으로 여러 이산수학 문제를 다루었던 에르되시와 달리 로바스의 연구 결과는 이론컴퓨터과학에 많은 파급 효과를 남겼습니다. 이제 로바스의 여러 연구 업적 중 몇 가지만 꼽아보도록 하겠습니다.
완벽 그래프 추측
완벽 그래프 추측은 1961년 프랑스인 수학자 버지Claude Berge가 만든 완벽 그래프perfect graph에 관한 추측입니다. 그래프 \(G\)의 채색수란 서로 이웃한 꼭짓점은 다른 색이 되도록 그래프의 꼭짓점에 색을 칠할 때 필요한 색의 수의 최솟값을 말하며 \(\chi(G)\)로 표기합니다. 그래프에서 채색수를 구하는 것이 그리 쉬운 문제는 아닙니다. 그래프의 채색수가 고작 \(3\) 이하인지 결정하는 문제조차도 쉽지 않다는, 즉 NP-complete이라는 결과가 1972년에 증명되어 있었습니다.
그래프의 채색수 값이 언제 큰지 쉽게 아는 방법으로, 그래프에 들어 있는 완전 그래프complete graph를 찾는 것을 생각해볼 수 있습니다. 완전 그래프란 모든 꼭짓점이 서로 이어진 그래프입니다. 만일 그래프에 꼭짓점 \(k\)개짜리 완전 그래프가 들어있다면, 그 꼭짓점 \(k\)개는 모두 서로 다른 색이 되어야 하므로 채색수가 \(k\) 이상이어야 합니다. 그러므로 그래프 \(G\)에 들어있는 가장 큰 완전 그래프의 꼭짓점 수를 \(\omega(G)\)라고 하면
\[
\chi(G)\ge \omega(G)
\]라는 부등식이 성립합니다.
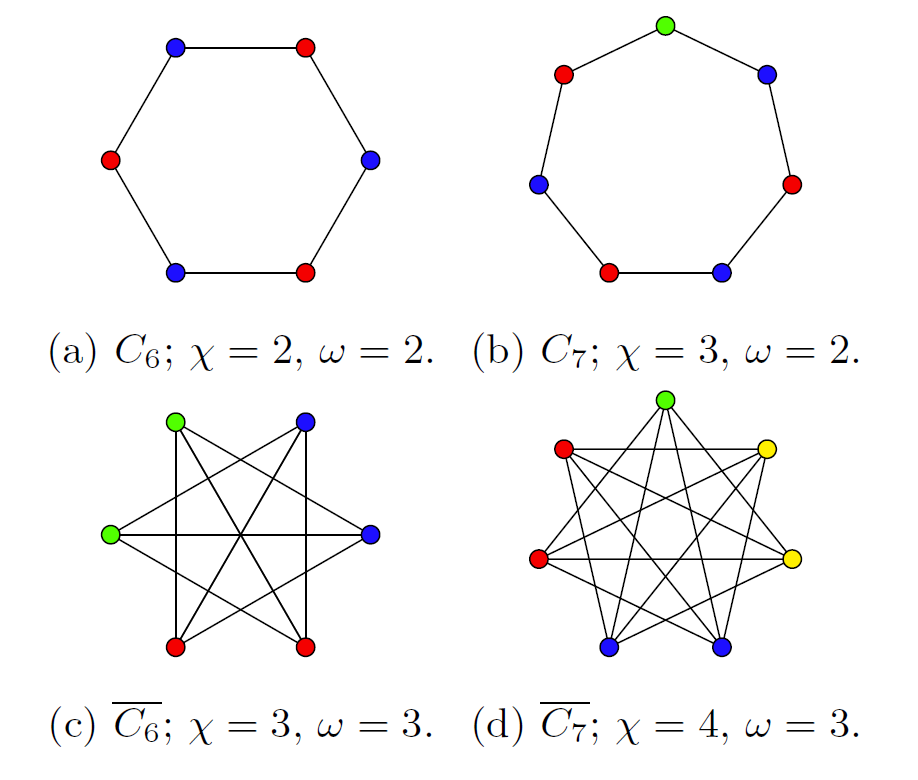
만일 어떤 그래프 \(G\)뿐만 아니라 \(G\)에서 꼭짓점 여러 개를 지워서 얻을 수 있는 모든 그래프 \(H\)에서 \(\chi(H)=\omega(H)\)가 성립하면 그 그래프 \(G\)를 완벽 그래프라고 합니다. 예를 들어 [그림4]에 있는 6각형처럼 생긴 그래프 \(C_6\)에서는 \(\chi(C_6)=\omega(C_6)=2\)이고 거기서 꼭짓점 여러 개 지워서 얻는 그래프에서도 항상 \(\chi=\omega\)라는 것을 알 수 있어서, \(C_6\)는 완벽 그래프입니다. 반면 7각형처럼 생긴 그래프 \(C_7\)에서는 \(\chi(C_7)=3\), \(\omega(C_7)=2\)라서 완벽 그래프가 아닙니다. 한편 그래프 \(G\)가 있을 때, 서로 이웃한 꼭짓점 사이에 있는 선은 지우고, 서로 이웃하지 않은 꼭짓점 사이에는 선을 넣어서 만든 새로운 그래프를 \(\overline{G}\)라고 씁니다. [그림4]를 살펴보면 \(\overline{C_6}\)은 완전 그래프이지만, \(\overline{C_7}\)은 완전 그래프가 아님을 알 수 있습니다.
완벽 그래프 추측은 \(G\)가 완벽 그래프면 \(\overline{G}\) 또한 완벽 그래프라는 추측입니다. 그래프 \(G\)의 \(\chi\)와 \(\omega\)가 같다고 해서 왜 \(\overline{G}\)에서도 같아야 하는지 전혀 연결이 없어 보이지만 신기하게도 많은 경우를 계산해보면 항상 그렇게 됩니다. 1972년 로바스는 이 추측을 해결하였습니다.
정리1 (로바스 1972) \(G\)가 완벽 그래프이면 \(\overline{G}\)도 완벽 그래프이다.
이 추측에 관하여 재미있는 이야기가 하나 있습니다. 미국의 수학자 풀커슨D. R. Fulkerson은 이 추측을 풀려고 몇 년간 노력하며 여러 결과를 내었지만, 한편으로 추측이 틀린 것은 아닐까 생각하며 반례를 찾으려고 몇 달 동안 노력하고 있었습니다. 그러던 중인 1971년 봄 어느 날 버지가 보낸 엽서를 하나 받았습니다. 엽서에는 로바스가 완벽 그래프 추측을 풀었다는 소식을 들었다는 글이 적혀있었습니다. 풀커슨은 그 소식을 듣자마자 책상 앞에서 이 추측에 다시 도전하였는데 다섯 시간 정도 지난 후 그동안 풀 수 없던 이 추측을 풀 수 있었다고 합니다. 이 이야기를 보면 수학 시험처럼 문제가 맞다는 것을 알고 도전하는 것보다 문제가 맞을지 틀릴지 모르는 추측에 도전하는 것이 얼마나 더 어려운 것인지 알 수 있습니다.
크네저 그래프의 채색수
1955년 독일의 수학자 크네저Martin Kneser는 독일 수학회에서 발간하는 저널에 아래와 같은 문제를 실었습니다.
“집합 \(\{1,2,\ldots,n\}\)의 부분집합 중 원소를 \(k\)개 가진 것들을 모아보자. 만일 \(n\ge 2k\)라면 이 집합들의 집합을 \(n-2k+2\)개 \(C_1\), \(C_2\), \(\ldots\), \(C_{n-2k+2}\)로 적당히 분할하여 각각의 \(C_i\)에 속한 두 집합의 교집합은 항상 공집합이 되지 않도록 할 수 있음을 알 수 있다. 그러면, 같은 성질이 되면서 \(n-2k+1\)개로 나누는 것은 가능할까?”
이 글을 읽으시는 분들은 \(n-2k+2\)개로 나누는 법을 찾으셨나요? 원소 \(1\)을 포함하는 크기 \(k\)인 부분집합들을 모아서 \(C_1\), 원소 \(2\)를 포함하면서 \(C_1\)에 안 들어가는 것들을 모아서 \(C_2\), …, 원소 \(n-2k+1\)를 포함하면서 \(C_1\), \(C_2\), \(\ldots\), \(C_{n-2k}\)에 포함되지 않은 것을 \(C_{n-2k+1}\)이라고 하고, 그때까지 아무 곳에도 포함되지 않는 크기 \(k\)인 부분집합들을 모아서 \(C_{n-2k+2}\)라고 하면 문제가 원하는 조건을 만족하는 것을 알 수 있습니다.
이 문제를 그래프의 채색 문제로 바꿀 수 있습니다. 집합 \(\{1,2,\ldots,n\}\)의 크기 \(k\)인 부분집합 각각을 꼭짓점으로 하고 두 부분집합 사이에 교집합이 공집합이 아니면 대응되는 꼭짓점 사이에 선을 넣은 그래프를 흔히 크네저 그래프Kneser graph라고 하고 보통 \(K(n,k)\)라고 씁니다. 크네저의 질문은 크네저 그래프의 채색수 \(\chi(K(n,k))\)가 \(n-2k+2\)인지 아니면 더 작은지 물어보는 것이었습니다.
질문이 나온 지 23년이 지난 1978년 로바스는 \(n-2k+1\)개로 잘 나누는 것은 불가능하다는 것을 증명합니다.
정리2 (로바스 1978) \(n\ge 2k\)이면, \(\chi(K(n,k))=n-2k+2\)이다.
로바스는 이를 증명하기 위해 놀랍게도 대수적 위상수학의 보석-울람 정리Borsuk-Ulam theorem를 사용하였습니다. 이산수학 분야에 대수적 위상수학 분야의 정리가 사용된 것은 이때가 처음이었습니다. 이 증명은 위상수학적 조합론topological combinatorics이라는 분야가 생기고 발전하게 된 계기가 되었습니다. 참고로 로바스의 증명이 나오고 나서 25년간은 대수적 위상수학을 쓰지 않고 크네저 그래프의 채색수를 결정하는 방법이 알려져 있지 않았습니다. 2004년이 되어서야 마투섹Jiří Matoušek이 비로소 크네저 그래프의 채색수를 보석-울람 정리를 쓰지 않고 그것과 관련된 조합적인 정리를 사용하여 조합적인 방법으로만 구해내는 증명을 만들었습니다.
혼선 그래프의 샤논 용량 문제
통신채널로 데이터를 전송하다 보면 노이즈 때문에 오류가 발생할 수 있습니다. 정보이론의 아버지라 불리는 미국의 수학자 샤논Claude Shannon은 1956년 통신채널에서 완벽하게 오류 없이 통신하고자 할 때 사용가능한 용량을 표현하기 위하여 그래프의 샤논 용량Shannon capicity이라는 개념을 제시하였습니다.
어떤 통신채널으로 문자를 전송한다고 가정해봅시다. 각각의 문자를 꼭짓점으로 하는 그래프 \(G\)를 만드는데, 통신채널로 전송했을 때 두 문자가 헷갈릴 가능성이 있으면 그 사이에 선을 그린 그래프 \(G\)를 혼선 그래프confusion graph라고 해봅시다.
예를 들어 혼선 그래프가 [그림6]의 5각형 \(C_5\)처럼 생겼다고 해봅시다. 이때 이 통신채널에서는 \(A\)와 \(C\) 문자만 사용하기로 하면 그 사이에는 선이 없으므로 절대 헷갈리지 않고 통신을 할 수 있습니다. 이때 한 글자당 보낼 수 있는 서로 다른 정보의 가짓수는 \(2\)가 됩니다.
하지만 통신채널에서 더 많은 데이터를 전송할 수도 있습니다. 연속한 두 글자를 묶어서 단어를 만들어서 전송한다면, 즉 AA, BC, CE, DB, ED라는 5개 단어로만 통신하기로 해봅시다. 여기서 만일 AA가 송신되었을 때 수신하는 사람이 BC로 헷갈릴 수 있을까요? 첫 글자는 A라서 B와 헷갈릴 수 있지만 두 번째 글자 A, C는 헷갈릴 수 없는 쌍이므로 AA를 착각하여 BC로 수신할 가능성은 없습니다. 마찬가지로 이 단어 5개에서는 어느 둘을 뽑아도 적어도 한 자리는 헷갈릴 수 없는 쌍이 들어있습니다. 따라서 이 통신채널에서 길이 2인 단어 5개로 통신하기로 하면 한 글자당 보낼 수 있는 서로 다른 정보의 가짓수는 기하 평균을 해보면 \(\sqrt{5}=2.236…\)이 되어 길이 1짜리 단어를 쓸 때의 가짓수 \(2\)보다 증가합니다. 즉 이렇게 두 글자씩 묶어서 보내면 같은 시간에 더 많은 용량의 정보를 오류 없이 전송할 수 있는 것이지요.
한 단어를 \(k\)개의 문자를 뽑아서 만들면 어떨까요? \(k\)개 문자로 단어를 뽑을 때 서로 헷갈리지 않게 하면서 가장 많이 뽑을 수 있는 단어의 수를 \(\alpha(G^k)\)라고 표현해봅시다. 이때 그래프 \(G\)의 샤논 용량은
\[c(G)=\sup_{k} \sqrt[k]{\alpha(G^k)}
\]라고 정의합니다.
한 단어를 문자 2개로 만드는 위의 방법 덕분에 \(c(C_5)\ge \sqrt{5}\)임을 알 수 있습니다.
그래프의 샤논 용량을 정확하게 결정하는 문제는 이 그래프의 꼭짓점 수가 아주 작더라도 매우 어려운 문제입니다. 아직까지도 7각형 그래프 \(C_7\)의 샤논 용량이 결정하는 문제가 조합론 분야 난제 중 하나입니다.
로바스는 1979년 논문에서 처음으로 \(C_5\)의 샤논 용량은 정확하게 \(\sqrt{5}\)라는 것을 증명합니다. 로바스가 증명하기 전에는 \(C_5\)의 샤논 용량은 \(\sqrt{5}\) 이상 \(2.5\) 이하라는 것만 알려져 있었습니다.
로바스는 이를 증명하기 위해서 로바스 세타 함수라고 불리는 함수 \(\vartheta(G)\)를 정의하였습니다. 먼저 대칭행렬 \(A\)의 고유치eigenvalue의 최댓값을 \(\lambda_{\max}(A)\)라고 쓰기로 합시다. 대칭행렬의 고유치는 실수임을 선형대수에서 배웁니다. 꼭지점이 \(n\)개인 그래프 \(G\)가 주어져 있을 때 \(i\)번째 꼭짓점이 \(j\)번째 꼭짓점과 이웃하지 않거나 \(i=j\)인 경우에는 \(a_{ij}=1\)이 되는 \(n\times n\) 대칭행렬 \(A=(a_{ij})\) 중 \(\lambda_{\max}(A)\)의 최솟값을 \(\vartheta(G)\)로 정의할 수 있습니다. 로바스는
\[
c(G)\le \vartheta(G)
\]
임을 증명하였고, \(\vartheta(C_5)=\sqrt{5}\)임을 보여서 \(c(C_5)=\sqrt{5}\)임을 처음으로 증명하게 되었습니다.
또한 로바스는 샌드위치 정리라고 하여
\[
\omega(G)\le \vartheta(\overline G)\le \chi(G)
\]라는 것도 증명하여서, 그래프가 완벽 그래프인 경우에는 \(\vartheta(\overline G)\)값이 \(\chi(G)\), \(\omega(G)\)값과 같다는 것도 보였습니다. 아울러 타원체ellipsoid 방법을 쓰면 로바스 세타 함수를 원하는 정밀도까지 효율적으로 다항식 시간 안에 구할 수 있기 때문에 완벽 그래프에서는 채색수 값을 다항식 시간 안에 구할 수 있다는 결과까지 얻어집니다. 이 방법을 쓰지 않고 순수하게 조합적인 방법으로 완벽 그래프의 채색수를 구하는 다항식 시간 알고리즘을 찾을 수 있는지는 아직 아무도 모르며 이 분야 중요한 미해결 문제입니다.
로바스 국소 보조정리
1975년 로바스와 에르되시가 쓴 논문에서 아래와 같은 확률 변수에 관한 보조정리가 등장합니다. 에르되시는 공동 논문이긴 해도 에르되시가 이것은 로바스가 만든 거라고 하였기에 보통 로바스 국소 보조정리Lovász Local Lemma라고 불리고 있습니다. 가장 간단한 형태를 적어보면 다음과 같습니다.
정리3 (로바스 국소 보조정리) \(A_1\), \(A_2\), \(\ldots\), \(A_k\)가 각각 확률 \(p\) 이하인 사건의 집합이며, 각각의 \(A_i\)는 나머지 \(A_j\) 중 최대 \(d\)개만 빼고 나머지들로 교집합, 여집합을 써서 만들 수 있는 모든 사건과 독립이라고 한다. 만일 \(4pd\le 1\)이면 \(A_1\), \(A_2\), \(\ldots\), \(A_k\) 모두 일어나지 않을 확률이 \(0\)보다 크다.
이것을 사용하면 여러 사건이 있을 때 일부 예외인 쌍만 빼면 대부분이 서로 독립인 경우 이 사건들이 모두 일어나지 않을 확률이 \(0\)보다 크다는 것이 증명됩니다. 그래프처럼 유한한 대상에서 쓰면 확률이 \(0\)보다 크다는 것은 어떤 성질을 만족하는 대상이 존재한다는 것을 의미하기 때문에 어떤 원하는 성질을 갖는 대상의 존재성을 증명할 때 매우 중요하게 사용됩니다. 예를 들어 램지수에 대한 하한을 정할 때 이걸 쓰면 상당히 괜찮은 하한을 얻을 수 있습니다.
LLL 알고리즘
선형대수학 과목을 배우면, \(n\)차원 공간에서 기저basis가 주어질 때 그람-슈미트 과정Gram-Schmidt process이라는 방법을 써서 정규직교기저orthonormal basis로 바꾸는 것을 배웁니다.
컴퓨터과학에서는 선형대수학에서 다루는 \(\mathbb{R}^n\)과 같은 연속한 공간보다는 \(\mathbb{Z}^n\)처럼 어떤 벡터들을 정수계수로 선형결합하여 얻을 수 있는 점들의 집합이 더 중요하게 쓰일 때가 많습니다. 예를 들어 \(\binom{6386}{51}\)과 \(\binom{71999}{575}\)라는 두 이차원 벡터를 가지고 생성할 수 있는 모든 벡터의 집합 \(L=\{a\binom{6386}{51}+b\binom{71999}{575}\}:a,b\in \mathbb{Z}\}\)을 고려해봅시다. 두 벡터 \(x\), \(y\)가 \(L\)에 들어가면 정수 \(a\), \(b\)에 대하여 \(ax+by\) 역시 \(L\)에 들어갑니다. 이런 집합을 격자lattice라고 부릅니다. 이 예에서는 \(575\binom{6386}{51}-51\binom{71999} {575}=\binom{1}{0}\)이고, \(-71999\binom{6386}{51}+6386\binom{71999}{575}=\binom{0}{1}\)이라서 \(L\) 안에 \(\binom{1}{0}\)과 \(\binom{0}{1}\)이 모두 들어가게 되고 따라서 \(L=\{a\binom{1}{0}+b\binom{0}{1}\}:a,b\in \mathbb{Z}\}\)이라고 간단하게 쓸 수 있습니다.
격자 \(L\)을 생성할 수 있게 해주는 최소한의 벡터의 집합을 기저라고 부르는데, LLL 알고리즘은 어떤 격자의 기저basis를 더 간단한 기저로 바꿔주는 알고리즘입니다. LLL 알고리즘은 로바스와 렌스트라 형제Arjen Lenstra와 Hendrik Lenstra가 1982년에 쓴 논문에 나오는 알고리즘이라 저자 세 명의 이름을 따서 LLL 알고리즘이라고 불립니다. 격자의 기저가 주어지면, 이제 LLL-reduced라고 불리는, 더 짧은 벡터로 구성된 기저를 찾아주는 다항식 시간 알고리즘입니다. 이 알고리즘은 특히 암호학 분야에 중요하게 활용되고 있으며 아벨상 위원회에서 언급한 로바스의 주요 업적 중 하나입니다.
로바스는 타원체 방법에 관한 책을 쓰는 중에 어떤 정리의 전제조건을 어떻게 하면 간단하게 할까 고민하다가 이 알고리즘을 만들었다고 합니다. 알고리즘을 렌스트라 형제에게 알렸더니 렌스트라 형제가 그걸 할 수 있으면 유리수 계수 다항식을 소인수분해 하는데 쓸 수 있다는 응용을 알아내어 함께 공동 논문을 쓰게 되었다고 합니다.
그래프 극한 이론
로바스가 마이크로소프트 연구소 이론 그룹에서 일할 때 어느 날 동료 연구자로부터 인터넷을 그래프로 나타낸 것처럼 매우 큰 그래프가 어떤 확률 분포에 따라서 무작위적으로 점점 커질 때, 큰 수의 법칙이나 중심 극한 정리 같은 것을 그래프에서도 말할 수 있는가라는 질문을 받았습니다. 그 질문에서 시작하여 로바스는 동료 연구자들과 함께 그래프 극한 이론graph limit theory라고 하는, 그래프이론이 해석학, 대수학, 실변수함수론, 이론컴퓨터과학 등 다양한 수학 분야와 연결되게 하는 아름다운 이론을 만들었습니다. 해석학을 공부하신 분은 그래프 극한 이론의 시작 부분을 매우 흥미롭게 읽을 수 있습니다. 그래프의 수열 \(G_1\), \(G_2\), \(\ldots\)이 언제 수렴하는가를 정의하기 위해서 그래프의 코시 수열Cauchy sequence을 정의하고, 그 극한값을 어떻게 표현하면 되겠는가를 연구하여 그래폰graphon이라는 대상을 정의합니다. 그래프 극한 이론의 내용은 헝가리의 다른 아벨상 수상자 세머레디의 주요 업적인 규칙성 보조정리regularity lemma와도 연결되는 등 매우 흥미로운 부분이 많습니다. 이제 그래프 극한 이론 분야도 매우 활발하게 연구되고 있습니다.
맺음말
이산수학 분야를 대표하는 로바스에 대한 글을 정리하면서 여러 일화를 찾아보고 인터뷰 영상도 보고 옛날 논문도 찾아보면서 필자 또한 재미있는 시간을 가졌습니다. 수학 내의 모든 연구분야가 그렇겠지만, 국내에는 로바스의 연구 분야와 관련이 있는 쪽의 이산수학 전공자가 많지 않아서 현재는 필자가 속한 KAIST를 제외하고는 국내에서는 학생들이 이렇게 재미있는 내용을 접할 기회가 거의 없는 상태입니다. 이 분야로 세계적인 연구를 하고 있는 한국인 젊은 연구자분들이 여럿 있는데, 대다수가 KAIST에서 학부 때 해당 내용을 접하고 관심을 가지기 시작하였습니다. 다른 대학 수학과 학생분들도 로바스처럼 고등학생 때 접하지는 못하더라도 이론컴퓨터과학과 함께 급속히 발전하고 있는 이산수학을 제대로 접할 수 있는 기회가 많아지길 기대해봅니다.