5월의 퍼즐에 참여해주신 모든 분들께 감사드립니다!
5월의 퍼즐에 참여해주신 분 중 정답과 함께 좋은 풀이를 보내주신 노건태님께
HORIZON에서 준비한 선물을 전달드릴 예정입니다.
이 문제는 전세계의 도시들이 겨루는 수학 올림피아드라 할 수 있는 도시대항 국제 수학 토너먼터Tournament of Towns, T.O.T의 2010년 가을 Junior O-레벨로 출제된 문제로, 출제자는 샤포발로프A. V. Shapovalov였다. HORIZON 2020년 8월 문제도 이 분의 문제였다. T.O.T에 대해 알고 싶은 분들은 국제 수학 토너먼트 홈페이지를 방문하면 된다.
한 칸에 상자가 여러 번 놓일 수 있으므로, 같은 칸에서 붉은 면이 있는 방향을 계속 바꿀 수 있다. 그러므로 필요한 경우 붉은 면이 향하는 방향을 바꾸면서 진행하면 격자판의 모든 칸을 지나가게 할 수 있다.
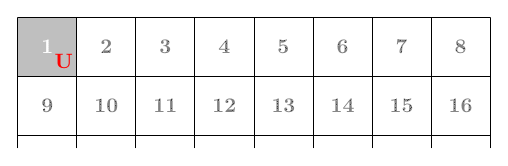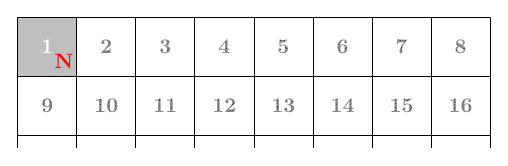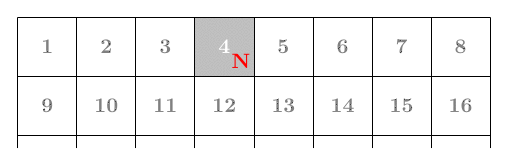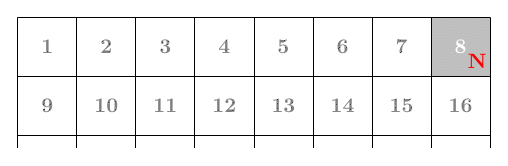
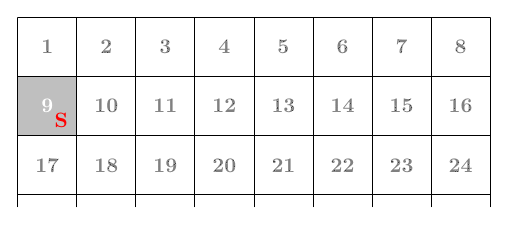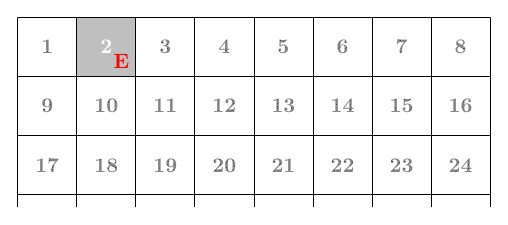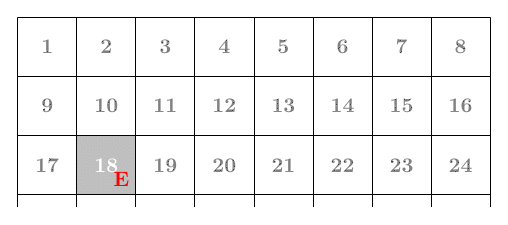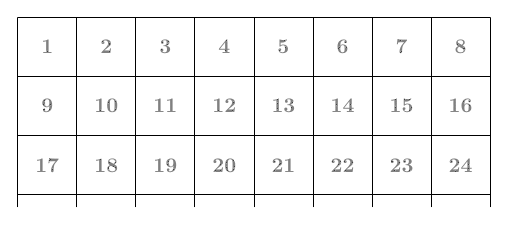
붉은 면이 향하고 있는 방향을 N, S, E, W로 나타내고 위쪽을 향하고 있는 경우는 U로 나타내자. 처음에 1번 칸에 붉은 면이 위로 놓여 있는 상황을 1U라 하면, 이 상자를 E 방향으로 굴린 결과는 2E가 된다. 상자를 1–2–10–9–1로 계속 옮기면 붉은 면이 있는 방향은
1U – 2E – 10E – 9U – 1N – 2N – 10U – 9W – 1W – 2U – 10S – 9S – 1U
가 되므로, 상자를 E–S–W–N으로 움직이면 U–N–W가 순환한다. 반대로 상자를 W–N–E–S로 움직이면 U–S–E가 순환한다.
이제 처음 상태인 1U에서 상자를 E–S–W–N으로 움직여 1N을 만든 다음, E 방향으로 계속 굴리면 격자판의 첫 번째 줄인 1번 칸부터 8번 칸까지 지날 수 있다.
8N 상태에서 S 방향으로 굴리면 16U가 되고, 여기서 상자를 W–N–E–S로 움직이면 16S가 된다. 이 상태에서 W 방향으로 계속 굴리면 격자판의 두 번째 줄을 16번 칸부터 9번 칸까지 지날 수 있다.

9S 상태에서 N–E–S–S–W로 굴리면 17U가 된다. 이제 1U에서 출발할 때와 같은 방식을 반복하면 나머지 모든 칸을 지날 수 있고, 57S로 끝나게 된다.
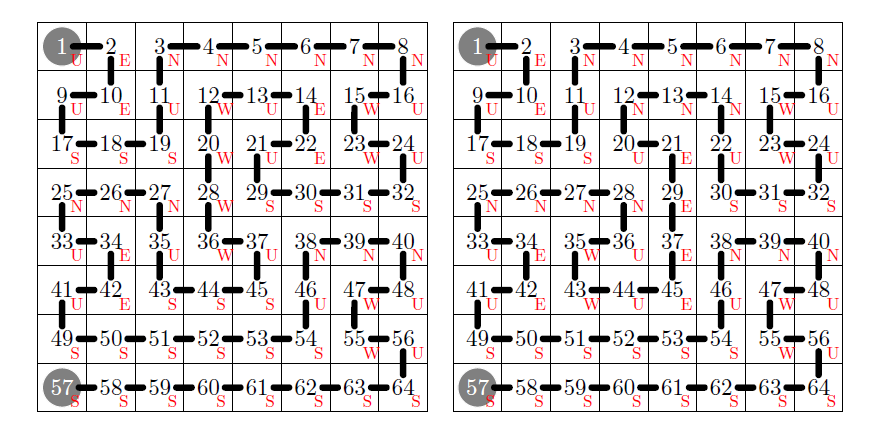
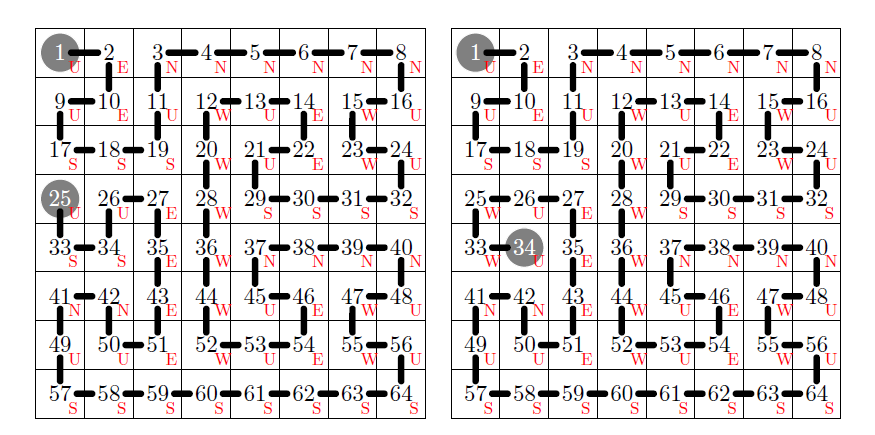
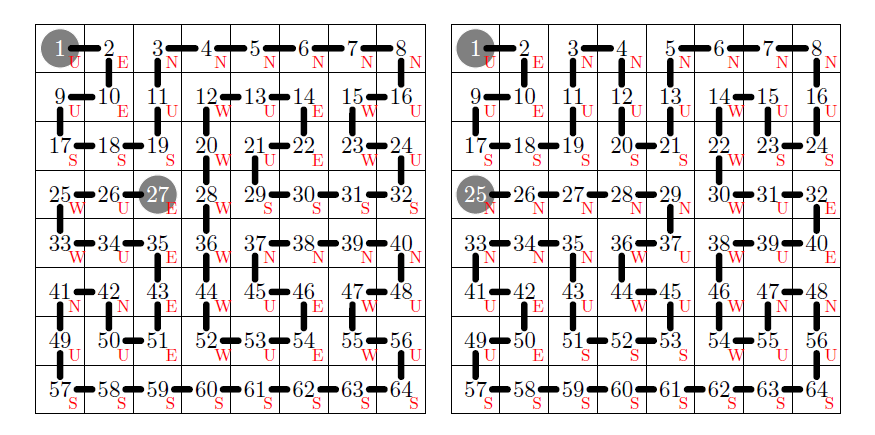
실은 이 문제는 조건을 더 강화하여, 모든 칸을 꼭 한 번씩만 지나게 할 수도 있다. 다음 그림이 그 여섯 가지 방법으로, 출발할 때 S 방향으로 굴리는 대칭적인 경우를 생각하면 총 경우의 수는 12가지이다.
다음은 5월의 정답자로 선정된 노건태님의 해설입니다.
편의상 1번부터 8번까지 적힌 줄을 1행으로 하고, 9번부터 16번까지 적힌 줄을 2행으로 하고, … , 57번부터 64번까지 적힌 줄을 8행이라고 하자.
1 -> 9 -> 10 -> 2, (S -> E -> N)
2 -> 10 -> 11 -> 3, (S -> E -> N)
3 -> 11 -> 12 -> 4, (S -> E -> N)
4 -> 12 -> 13 -> 5, (S -> E -> N)
5 -> 13 -> 14 -> 6, (S -> E -> N)
6 -> 14 -> 15 -> 7, (S -> E -> N)
7 -> 15 -> 16 -> 8 (S -> E -> N)
위와 같이 남 -> 동 -> 북 방향으로 7번을 연속해서 진행하면 문제의 조건을 만족하면서 1행과 2행에 있는 모든 칸을 도달할 수 있다. 위와 같은 과정을 거치면 1행에 도달하는 모든 순간은 항상 위쪽 면이 붉은 면이며, 시작 위치인 1번과 동일하게 종료 위치인 8번에서도 붉은 면은 위쪽을 향하고 있다.
설명의 편의를 위해, 위와 같이 진행한 다음에 1번으로 돌아가보자. 여러 방법이 있겠지만 가장 쉬운 방법은 다음과 같이 남 -> 서쪽으로 7번 -> 북 방향으로 이동하는 것이다. 1번 위치로 되돌아왔을 때 붉은 면은 여전히 위쪽을 향하고 있다.
8 -> 16 -> 15 -> 14 -> 13 -> 12 -> 11 -> 10 -> 9 -> 1
(S -> W -> W -> W -> W ->W -> W ->W -> N)
이제 1번에서 17번으로 다음과 같이 동 -> 남 -> 남 -> 서 방향으로 이동해보자. 시작 위치인 1번과 동일하게 종료 위치인 17번에서도 붉은 면은 위쪽을 향하고 있다.
1 -> 2 -> 10 -> 18 -> 17
(E -> S -> S -> W)
이렇게 이동하면 1번에서의 상태와 17번에서의 상태가 동일해진다. 즉, 1번에서 시작하여 1행과 2행을 모두 방문한 후 1번으로 되돌아오는 형태를 17번에서 시작하면 문제의 조건을 만족하면서 3행과 4행에 있는 모든 칸에 도달한 후 17번으로 되돌아올 수 있다. 이와 동일한 과정으로 17번에서 33번으로 이동하여 5행과 6행에 있는 모든 칸에 도달할 수 있으며, 33번에서 45번으로 이동하여 7행과 8행에 있는 모든 칸에 도달할 수 있다.
결과적으로, 붉은 면이 겉으로 드러나게 이동하면서 모든 칸을 상자가 지나갈 수 있다.
P.S. 더 적은 횟수로의 이동을 위해서는 1행과 2행을 모두 방문한 다음, 8번에서 1번으로 돌아갔다가 17번으로 가는 것이 아니라, 8 -> 7 -> 15 -> 23 -> 24로 이동하여 24번에서 시작하여 3행과 4행을 역으로 방문하는 것이 더 나은 방법이다. 마찬가지로 7행과 8열도 역으로 방문하여 방문 횟수를 줄일 수 있다. 단, 방법이 가장 효율적인 이동 경로는 아니며, 더 최적화된 방문 경로가 존재한다. 다만 본 문제에서는 방문이 가능한지의 여부를 따지는 것이기 때문에, 가장 효율적인 이동 경로를 찾는 과정은 생략하기로 한다.