정규분포와 보편성과 랜덤 행렬

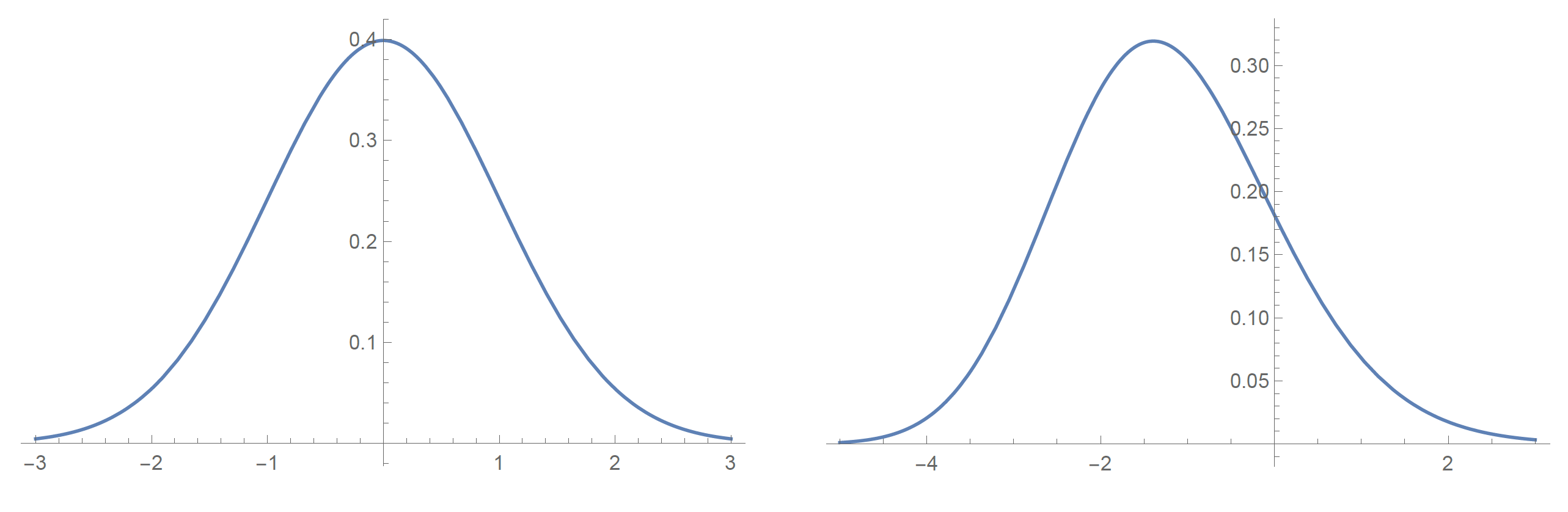
충분히 큰 계^system의 성질은 구성요소의 구체적인 성질과 무관하다. 이를 보편성^universality이라 한다.

어떤 확률변수를 사용해야 할까?

작은 입자의 움직임, 무선통신에서 나타나는 잡음, 주식 시장의 가격 변동 등, 자연현상과 사회현상에서 관측되는 많은 자료는 근본적으로 무작위적^random이거나 인과 관계를 파악하는 것이 매우 어려워서 확률적인 방법을 사용하여 분석하는 것이 유리한 경우가 많다. 여기서 확률적인 방법이란 현상에 대응하는 수학적 모형을 만들 때 확률변수^{random variable}를 사용한다는 의미로 생각할 수 있다.

실제로 확률적인 방법을 적용하는 경우, 첫 번째로 맞닥뜨리게 되는 문제는 구체적으로 어떤 확률분포를 따르는 변수를 사용하는지에 관한 것이다. 정규^normal분포, 베르누이^Bernoulli분포, 이항^binomial분포, 포와송^Poisson분포, 감마^gamma분포 등 수많은 분포가 있으며, 상황에 따라 알맞은 분포를 사용하는 것이 바람직하다. 그러나 실제로는 어떤 확률 분포가 적합한지 파악하는 것이 어려운 경우가 많은데, 이런 경우 정규분포를 사용하는 것이 일반적이다. 참고로, 평균 \(\mu\), 분산 \(\sigma^2\)인 경우, 정규분포의 확률밀도함수^{probability density function}는 다음과 같다.

\[
p(x) = \frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}
\]
위 함수의 계수는 확률밀도함수가 되도록, 즉 적분값이 \(1\)이 되도록 맞춰진 값이며, 적분값이 \(1\)이 아닌 일반적인 경우에는 가우시안함수^{Gaussian function}가 된다. 본문에서는 오해의 소지가 없는 한 정규분포의 확률밀도함수와 가우시안 함수를 모두 정규분포로 표기하려 한다.

정규분포의 특수성

정규분포의 확률밀도함수는 다양한 성질을 가지고 있다. 특기할만한 사항은 다음과 같다.

정규분포를 따르는 서로 독립인 확률변수의 합은 정규분포를 따른다.
평균이 \(0\)인 정규분포의 푸리에 변환^{Fourier transform}은 가우시안 함수이다. 특히, 분산이 \(1\)인 표준정규분포^{standard normal distribution}는 푸리에 변환의 고유함수^{eigenfunction}이다. 푸리에 변환은 확률론의 특성함수^{characteristic function}에 해당하므로, 이 성질은 정규분포와 관련된 증명에 유용하게 사용할 수 있다.
분산이 일정할 때, 정규분포를 따르는 확률변수의 엔트로피가 가장 크다. 참고로 확률밀도함수가 \(f(x)\)인 확률변수의 엔트로피는 \(\int_{-\infty}^{\infty} f(x) \log f(x)\,dx\)이다.
특정한 위치에 있던 입자의 운동이 확산 방정식^{diffusion equation} (또는 열 방정식^{heat equation})을 따를 때, 일정한 시간이 지난 뒤 입자의 위치는 정규분포 형태로 나타난다. 이로 인해 브라운 운동을 하는 입자의 위치 또한 정규분포를 따른다.
중심극한정리^{central limit theorem}에서 극한값이 정규분포로 나타난다.

이 외에도, 정규분포는 불확정성의 원리^{uncertainty principle}, 로그-소볼레프 부등식^{log-Sobolev inequality}의 등호조건을 만족시키는 등 다양한 특성을 가지고 있다. 이 중에서 가장 관심을 끄는 것은 바로 중심극한정리에 대한 부분이다.

중심극한정리와 보편성

서로 독립이며 동일한 분포를 가진 확률변수 \(X_1,X_2,…,X_n\)이 있다고 하자. 편의상 \(X_i\)의 평균은 \(0\), 분산은 \(\sigma^2\)이라 하면, 표본평균^{sample mean}의 \(\sqrt{n}\)배, 즉 \(\tilde{X}_n = (X_1 + X_2 + \dots + X_n)/\sqrt{n}\)은 평균 \(0\), 분산 \(\sigma^2\)인 정규분포로 분포수렴^{convergence in distribution}한다. 이는 중심극한정리의 기본적인 형태에 해당한다.

여기서 중요한 점은 확률변수 \(X_i\)가 어떤 분포를 따르는가에 상관없이 \(\tilde{X}_n\)는 항상 정규분포로 수렴한다는 것이다. 이를 통해 확률변수에 관한 정보가 부족할 때 정규분포를 사용하는 이유를 이해할 수 있다. 수학적 모형에서 필요한 무작위성을 이해하기 어려운 상황이라는 것은 결국 이 무작위성이 여러 가지 원인이 복합적으로 작용하여 발생한 결과일 수 있다는 뜻일 수 있는데, 그렇다면 중심극한정리에서 볼 수 있듯이 그 결과물을 정규분포를 따르는 확률변수로 가정하는 것이 합리적이기 때문이다.

중심극한정리에는 보편성의 원리가 잘 나타나 있다. 확률변수 \(X_i\)의 특성은 최종 결과물인 정규분포에 반영되지 않고, 단지 그 분산인 \(\sigma^2\)만 정규분포의 분산으로 남을 뿐이다. 이러한 성질은 린드버그 교환^{Lindeberg replacement}에 의한 중심극한정리의 증명에서 극명하게 드러난다. 린드버그 교환이란, \(\tilde{X}_n\)을 구성하고 있는 각 확률변수를 하나씩 다른 확률변수로 교체하는 과정을 의미한다. 만약 각각의 \(X_i\)가 특정한 분포를 따르는 경우 중심극한정리가 성립함을 보이고, 각 \(X_i\)의 분포를 다른 분포로 바꿀 때마다 \(\tilde{X}_n\)의 변화량이 \(1/n\)보다 훨씬 작음을 증명한다면, \(X_i\)가 어떤 분포를 따르더라도 중심극한정리가 성립함이 증명된다. (세부적인 내용을 알기 원하는 독자를 위해 본문의 끝부분에 린드버그 교환에 의한 중심극한정리의 증명을 더 자세히 설명하였다.)

린드버그 교환에 의한 중심극한정리의 증명에서 눈여겨볼 부분은 정리의 결론 부분, 즉 정규분포로 수렴한다는 사실이 특수한 경우에만 다루어진다는 것이다. 일반적으로는 증명의 편의상 \(X_i\)가 정규분포를 따르는 경우를 고려하지만, 필요하다면 드무아브르^{de Moivre}가 증명한 것처럼 \(X_i\)가 이항분포를 따르는 경우에 \(\tilde{X}_n\)이 정규분포로 수렴한다는 사실을 사용할 수도 있다. 꼭 린드버그 교환을 사용하지 않더라도, 보편성의 원리가 적용되는 정리를 증명할 때 이처럼 특수한 경우의 증명을 먼저 한 뒤 일반적인 경우로 확장해도 증명의 결론이 변하지 않음을 보이는 방법이 사용되는 경우가 많다.

보편성의 관점에서 확률변수에 관한 정보가 부족할 때 정규분포를 사용하는 이유를 다시 생각해 보자. 수학적 모형에 보편성의 원리가 적용된다면 사실은 사용하는 확률변수의 종류와 관계없이 원하는 결과를 얻을 수 있는 상황일 수 있다. 그렇더라도 여전히 정규분포를 사용하는 것을 우선적으로 고려할 만하다. 위에서 설명한 것과 같이 정규분포는 여러 가지 특수한 성질을 가지고 있어 계산과 분석이 용이하기 때문이다.

랜덤 행렬과 보편성

중심극한정리를 통해 서로 독립이며 동일한 분포를 가진 확률변수의 합의 성질을 이해할 수 있지만, 수학적 모형이 복잡해지면 단순히 확률변수의 합을 사용하는 것이 아니라 더 복잡한 함수를 고려해야 한다. 복잡도가 더 큰 수학적 모형의 대표적인 예가 랜덤 행렬이다. 랜덤 행렬은 각 성분이 확률변수인 행렬을 의미한다. 랜덤 행렬 연구에도 다양한 주제가 있으나, 가장 대표적인 것은 고유치^eigenvalue에 관한 연구이다. 행렬의 고유치는 특성방정식^{characteristic equation}의 해이며, 특성방정식의 계수는 행렬의 성분으로 이루어진 복잡한 다항식이므로 행렬을 이루고 있는 각 확률변수가 고유치에 미치는 영향은 중심극한정리에서와 같이 단순한 형태가 아니다. 물리학 용어를 빌리자면, 랜덤 행렬은 강한 상관관계가 있는 계^{strongly correlated system}이다.

랜덤 행렬 중 가장 대표적인 것은 위그너 행렬^{Wigner matrix}이다. 확률변수가 실수인 경우로 한정하면, 위그너 행렬은 실대칭^{real symmetric} 랜덤 행렬 중 상삼각^{upper triangular} 부분의 성분이 서로 독립이며 동일한 분포를 가지는 것을 뜻한다. 대칭성으로 인해 위그너 행렬의 고유치는 모두 실수이다. 위그너 행렬에 대한 다양한 연구 주제가 있으나, 여기서는 위그너 행렬의 가장 큰 고유치를 중점적으로 다루고자 한다.

크기가 \(n\)인 위그너 행렬에서 각 성분의 평균은 \(0\), 분산은 \(1\)이라 하자. 가장 큰 고유치를 \(\mu_1\)이라 하면, \(\mu_1\)은 \(2\sqrt{n}\)에 가까운 값을 가지며 그 변동의 폭은 \(n^{1/6}\) 정도의 크기임이 잘 알려져 있다. 나아가, \(\mu_1\)의 변동의 성질, 구체적으로는 \(n^{1/6} (\mu_1-2\sqrt{n})\)이 어떤 분포로 수렴하는지 또한 알려져 있으며, 이 분포를 흔히 트레이시-위덤^Tracy-Widom분포라 한다. 이 결과에는 보편성의 원리가 적용되어 위그너 행렬을 구성하는 확률변수의 종류와 상관없이 성립하며, 이를 랜덤 행렬 이론에서는 끝보편성^{edge universality}이라 한다.

트레이시-위덤 분포와 확장된 보편성

트레이시-위덤 분포는 랜덤 행렬의 가장 큰 고유치에서만 나타나는 것이 아니다. 무작위성이 포함된 성장모형^{growth model}인 KPZ^{Kardar-Parisi-Zhang} 방정식에서 해의 변동^fluctuation, 즉 고정된 한 점이 성장한 정도에서 결정론적인^{deterministic} 부분을 제외하고 남은 부분은 트레이시-위덤 분포를 따른다. 불규칙적인 물질 내에서 액체의 흐름을 나타내는 투과^percolation모형에서도 트레이시-위덤 분포를 찾을 수 있다.

트레이시-위덤 분포가 나타나는 가장 놀라운 예는 아마도 최대증가부분수열^{longest increasing subsequence}문제일 것이다. \(1\)부터 \(n\)까지의 자연수로 이루어진 순열^permutation의 부분수열 중 증가수열인 것을 증가부분수열이라 하고, 이 중 가장 길이가 긴 것을 최대증가부분수열이라 한다. 예를 들어, \(n=5\)일 때 순열 \((1 5 4 2 3)\)을 생각하면, \((1 4)\), \((1 2 3)\)등이 증가부분수열이며, \((1 2 3)\)이 최대증가부분수열이다. 가능한 모든 순열에 대해 최대증가부분수열의 크기를 계산하여 통계적 분포를 구하면 트레이시-위덤 분포로 수렴함이 알려져 있다.

트레이시-위덤 분포가 랜덤 행렬 외의 다른 모형에서도 나타나는 현상은, 단순한 랜덤 행렬 이론의 보편성을 뛰어넘는 것으로, 확장된 보편성이라 부르는 것이 적당해 보인다. 일반적으로 강한 상관관계가 있는 계에서는 확장된 보편성이 성립할 것으로 생각되지만, 이에 관해 통합된 결과가 수학적으로 증명된 바는 없으며, 개별 모형마다 다른 방법론을 적용하여 별개의 결과가 증명되고 있다. 보통, 주어진 모형에서 강한 상관관계가 있을 것으로 추정되는 경우, 그리고 계산을 통해 얻은 분포가 비대칭적인 경우 트레이시-위덤 분포가 나타날 가능성을 고려할 만하다.

트레이시-위덤 분포가 나타나는 예를 통해 알 수 있듯이, 보편성이 적용되는 경우라 하더라도 그 결과물이 반드시 정규분포일 필요는 없다. 그럼에도 불구하고, 위에서 설명한 것과 같이 정규분포는 여러 가지 특수한 성질 때문에 여전히 큰 의미를 지닌다. 실제로, 트레이시-위덤 분포가 처음으로 증명된 확률 모형은 가우시안 직교행렬^{Gaussian orthogonal ensemble}인데, 이는 위그너 행렬에서 각 성분이 정규분포를 따르는 경우에 해당한다. 나아가, 확장된 보편성의 관점에서 생각해 보면 여러 가지 수학적 모형에서 유사한 결과가 나타나게 되므로 그중에서 가장 계산과 분석이 용이한 모형을 다루는 것이 유리한데, 랜덤 행렬이 이에 해당하는 경우가 많다.

다시 처음의 질문으로 되돌아가자. 확률적인 개념이 포함된 수학적 모형을 사용할 때, 어떤 확률변수를 사용해야 할지 고민이 된다면 그냥 정규분포를 사용하는 것이 좋다. 만약 다른 특정한 분포가 정규분포보다 사용하기에 편하다면 그렇게 하는 것도 좋아 보인다. 확률분포에 대한 고민을 하지 않는 것은 수학적 모형에 대한 이해가 부족한 까닭이 아니라 확률적인 개념이 포함된 수학적 모형의 보편성에 대한 충분한 이해가 뒷받침되기 때문이다. 단순함 속에 심오한 진리가 감춰져 있는 수학의 특성이 여기서도 나타나고 있다.

린드버그 교환을 통한 중심극한정리의 증명

먼저, 정규분포를 따르며 서로 독립이고 분산이 \(\sigma^2\)인 확률변수 \(Y_i\)를 생각하자. 그리고, \(\tilde{X}_n^{(0)} = (Y_1+Y_2+ \dots +Y_n )/ \sqrt{n}\)이라 하자. 그러면, \(Y_i\)가 서로 독립인 조건에 의해 \(\tilde{X}_n^{(0)}\)이 정규분포를 따르는 것과 그 분산이 \(Y_i\)의 분산과 일치함을 알 수 있다.
일반적인 확률변수 \(X_i\)에 대해 중심극한정리를 증명하기 위하여, \(\tilde{X}_n^{(0)}\)의 정의에서 \(Y_1,Y_2,\dots,Y_i\)가 \(X_1,X_2,\dots,X_i\)로 대체된 것을 \(\tilde{X}_n^{(i)}\)라 하자. 즉, \(\tilde{X}_n^{(i)}=(X_1+X_2+\dots+X_i+Y_{i+1}+\dots+Y_n )/\sqrt{n}\)이다. 모든 \(Y_i\)가 \(X_i\)로 대체된 \(\tilde{X}_n^{(n)}\)는 \(\tilde{X}_n\)와 일치한다.
중심극한정리에서 다루는 수렴이 분포수렴이고, \(\tilde{X}_n^{(0)}\)가 정규분포를 따른다는 성질로부터, 만약 임의의 자연수 \(k\)에 대해 \(\tilde{X}_n\)의 \(k\)번째 모멘트의 극한값, 즉 \([X_n ]^k\)의 평균의 극한값이 \(\tilde{X}_n^{(0)}\)의 \(k\)번째 모멘트(의 극한값)와 일치한다면 \(\tilde{X}_n\)이 정규분포로 수렴함을 알 수 있다.
\([\tilde{X}_n^{(i)}]^k\)와 \([\tilde{X}_n^{(i-1)}]^k\)의 차이는 전자에 포함되어 있는 \(X_i\)가 후자에는 \(Y_i\)로 대체되어 있다는 것 뿐이다. \(\tilde{X}_n^{(i)}\)의 정의에 포함된 \(1/\sqrt{n}\)을 함께 고려하여 이항정리^{binomial theorem}를 적용하면, 이 차이는 결국 \(E[N^{-p/2} (X_i )^p f(X_1,X_2,\dots,X_{i-1},Y_{i+1},\dots,Y_n )]\)형태의 항이 \(E[N^{-p/2} (Y_i )^p f(X_1,X_2,\dots,X_{i-1},Y_{i+1},\dots,Y_n )]\)로 바뀐 것이다. (여기서 \(E\)는 평균을 의미한다. \(f\)는 적당한 다항식이며, 평균을 취했을 때 발산하지 않는다.) 그런데, \(X_i\)나 \(Y_i\)가 다른 확률변수와 서로 독립이고, \(p=1,2\)에 대해 \(E[N^{-p/2} (X_i )^p]=E[N^{-p/2} (Y_i )^p]\)이므로, \(E[\tilde{X}_n^{(i)}]^k-E[\tilde{X}_n^{(i-1)}]^k=o(N^{-1})\)임을 증명할 수 있다.
\(E[\tilde{X}_n]^k-E[\tilde{X}_n^{(0)}]^k=\sum_{i=1}^n (E[\tilde{X}_n^{(i)}]^k-E[\tilde{X}_n^{(i-1)}]^k)\)을 통해서 \(E[\tilde{X}_n]^k-E[\tilde{X}_n^{(0)}]^k\)가 \(0\)으로 수렴함을 알 수 있다. 따라서, \(\tilde{X}_n\)이 정규분포로 수렴함이 증명되었다.