기하를 품는 산술

얼핏 보면 서로 관련이 없어 보이는 현상들도, 파고 들어가 보면 밀접하게 연결이 되어있는 경우가 수학에서는 많이 있습니다. 이 글에서는 기하학의 근본적인 정리 중 하나인 수축량 부등식^{systolic inequality} 을 소개하고, 이 정리가 정수론적인 문제 풀이에 쓰이는 예를 가벼운 마음으로 살펴보겠습니다.

근본적인 정리

한여름 해수욕장에서 볼 수 있을법한, 공기를 불어넣은 고무 튜브를 생각해 봅시다. 주변에 비슷한 물건을 가지고 있다면 직접 실험해 볼 수도 있겠습니다. 이 튜브를 이루는 곡면은 위상적으로 2차원 토러스^torus 라고 불립니다. 튜브의 면적에 일정한 값 \(A\)를 주었을 때,¹ 튜브는 모양에 따라 훌라후프처럼 얇고 길 수도, 또는 갓 구워져 나온 베이글처럼 뚱뚱할 수도 있습니다. 이러한 튜브에 적당한 단일폐곡선^{simple closed curve} 을 그리고 가위로 자르면, 빈 원통형의 곡면을 얻을 수 있습니다.([그림1]) 여기서 자연스럽게 나오는 기하학적인 질문이 있습니다.

질문. 튜브에 그릴 수 있는 가장 짧은 단일폐곡선의 길이를 \(L\)이라 할 때, \(L\)을 튜브의 모양에 관계 없이 면적 \(A\)만의 함수로 상한을 줄 수 있을까?

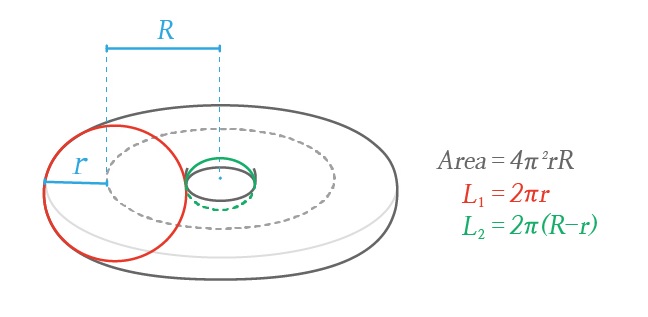
예를 들어 주어진 튜브가, 반지름이 \(r\)인 원을 중심에서부터 거리가 \(R>r\) 인 축을 상대로 회전 시켜 만든 원환면이라 가정하고, 간단한 계산을 해봅시다. 먼저 이 튜브의 면적은, 미적분을 이용해

\(A=4\pi^2rR\)

임을 보일수 있습니다. 다음, 닫힌 곡선을 두 가지 방법으로 그려봅시다.[그림2]

• 튜브의 단면인 반지름 \(r\)의 원을 따라 그린 곡선의 길이는 \(L_1=2\pi r\) 입니다.
• 튜브의 가장 안쪽을 따라 그린 원의 둘레는 \(L_2=2\pi(R-r)\) 입니다.

이 둘을 곱하여 보면

\(L_1L_2=4\pi^2r(R-r)=4\pi^2rR-4\pi^2r^2=A-4\pi^2r^2\leq A\)

이므로, 상황에 따라 \(L_1\) 또는 \(L_2\) 길이의 폐곡선을 선택하면, 가능한 최소 길이 \(L\)는 항상 \(A\)의 제곱근보다 작거나 같음을 알 수 있습니다. 물론, 현실에서처럼 튜브가 찌그러지거나 튀어나온 부분이 있을 경우, 해답은 더 복잡해집니다.

더 나아가 위와 같은 질문은, 리만 계량^{Riemannian metric} 이 주어진 임의 다양체 위의 곡선에 대한 문제로 확장시킬수 있습니다. 어떤 컴팩트한 \(n\)차원의 리만 다양체 \((M,g)\) 가 있을 때, \((M,g)\)의 수축량 \(Systole(M,g)\) 를 축약불가능한 닫힌 곡선 길이의 하한으로 정의합시다. 여기서 물어볼 수 있는 것은, 다양체의 \(n\)차원 부피 \(Volume(M,g)\) 와 수축량 \(Systole(M,g)\) 사이의 관계입니다. 이차원 토러스에 대하여, , 뢰브너^{Charles Loewner} 는 1949년에 다음을 증명하였습니다.

뢰브너의 정리 (1949). 2차원 토러스 \(T\) 에 임의의 리만 계량 \(g\)가 주어졌을 때, 다음을 만족한다:

  \(Systole(T,g)^2\leq \frac{2}{\sqrt{3}}Area(T,g).\)

즉 위의 부등식은, 튜브가 어떤 모양을 가지던지, 면적이 정해지면 위의 부등식에 따른 길이의 축약불가능한 단일폐곡선을 항상 찾을 수 있다는 것을 의미합니다. 이와 같이 리만 다양체들의 수축량을 연구하는 학문을 수축량 기하학^{systolic geometry} 이라 합니다. 필즈 메달리스트 르네 톰^{Rene Thom} 은, 60년대 초반 마르셀 베르제 ^{Marcel Berger} 와 대화 중 수축량 부등식 결과들에 대하여 듣자 말하였습니다:

수축량을 부피의 함수로 상한을 주는 부등식은, 이차원 토러스를 넘어 다른 컴팩트 곡면으로, 또 1983년[1] 그로모프^{Mikhael Leonidovich Gromov} 를 통해 \(n\)차원의 본질적 다양체^{essential manifold} 으로까지 확장되었습니다.

그로모프의 정리 (1983). 차원수 \(n\)이 주어졌을 때, 다음을 만족시키는 상수 \(C_n\)이 존재한다: 임의의 \(n\)차원 본질적 리만 다양체 \((M,g)\) 가 있으면,

\(Systole(M,g)^n\leq C_nVolume(M,g).\)

본질적 다양체의 예로는 튜브를 다차원으로 확장시킨 \(n\)차원 토러스를 들 수 있습니다. 위상적으로 \(n\)차원 토러스는 원을 \(n\)번 곱한 \(S^1\times\cdots\times S^1\) 다양체입니다. 참고로 뢰브너의 정리 전에, \(n\)차원 토러스^{flat torus} 에 대해서는 수축량 부등식이 이미 잘 알려져 있었습니다. 여기서 \(n\)차원 평평한 토러스는, 유클리드 공간 \(\mathbb{R}^n\) 안에서 \(n\)개의 독립된 벡터들로 생성된 격자 군 \(L\simeq\mathbb{Z}^n\) 의 몫인 \(T=\mathbb{R}^n/L\) 의 꼴로 나타내어지며, \(\mathbb{R}^n\) 위의 표준 계량이 \(T\) 위에 평평한 계량 \(g\)를 정의합니다. 다음은 민코프스키^{Hermann Minkowski} 가 설립한 이론인 수의 기하학^{geometry of numbers} 의 정리 중 하나를, 평평한 토러스의 수축량에 대한 결과로 번역한 것입니다.

민코프스키의 정리 (1889). 임의 \(n\)차원의 평평한 토러스 \(T\) 가 주어졌을 때,

\(\omega_nSystole(T)^n\leq 2^nVolume(T).\)

여기서 \(\omega_n\) 는 \(n\)차원 단위공의 부피를 가리킨다.

위 정리의 증명은 다음과 같습니다. 평평한 토러스 \(T\) 위의 가장 짧은 닫힌 측지선 ^{closed geodesic} 의 길이를 \(L\)이라고 합시다. 이 측지선을 지름으로 가진 \(n\)차원 공을 토러스 위에 그려보면, \(L\)의 정의에 따르면 인해 공의 내부는 자기 자신과 맞닿는 부분이 없어야 한다는 것을 알 수 있습니다. 그러므로 공의 부피는 \(T\)의 부피보다 작거나 같아야 하는데, 공의 부피는 정확히 \(\omega_n(L/2)^n\) 이므로 위의 부등식이 성립합니다.

흥미로운 점은, 민코프스키는 위의 결과를 정수론의 문제들을 생각하다 발견하게 되었다는 것입니다! 다음 장에서는 정수론에서 중심적으로 다루어지는 디오판토스 방정식들에 대하여 소개하겠습니다.

디오판토스 방정식

정수론은 근본적으로 \(0,\pm1,\pm2,\dots\) 들과 덧셈, 곱셈 등의 작용에 대한 정수 체계의 구조를 살피는 학문입니다. 정수들 사이의 구조를 효과적으로 표현하는 방법 중 하나는 방정식을 이용하는 것입니다. 일반적으로, 구하는 답이 정수해인 방정식이 주어졌을때, 이를 디오판토스 방정식이라 칭합니다. (디오판토스^{Diophantus of Alexandria}) 는 방정식의 정수해에 대하여 연구한 고대 그리스 (c. AD 200-300) 의 수학자였습니다.) 디오판토스 방정식을 써서 나타낼 수 있는 정수론의 대표적인 결과 중 하나로는, 라그랑주^{Joseph Louis Lagrange} 의 다음 정리가 있습니다.

라그랑주의 정리 (1770). 모든 양의 정수는 4개 제곱수의 합으로 나타낼 수 있다. 즉, 임의의 자연수 \(k\)에 대하여 다음의 방정식은 정수해 \((x,y,z,w)\) 를 갖는다:

\begin{align*}
\tag{1}
x^2+y^2+z^2+w^2=k.
\end{align*}

예로 \(13=2^2+2^2+2^2+1^2\) 그리고 \(2021=42^2+16^2+1^2+0^2\) 임을 볼 수 있습니다. 디오판토스 방정식의 매력은, 문제의 간단명료함, 그리고 그에 반한 해법의 깊이와 어려움이 자주 공존한다는 것입니다. 예를 들어, 다음의 문제는 놀랍게도 아직 풀리지 않았습니다.

추측. 정수 \(k\)를 \(9\)로 나눈 나머지가 \(4\)나 \(5\)가 아닐 때, 다음 방정식이 정수해 \((x,y,z)\) 를 갖는다:

\begin{align*}
\tag{2} x^3+y^3+z^3=k.
\end{align*}

언뜻 보면 \((1)\) 과 \((2)\) 두개의 방정식은 더해지는 변수들의 차수가 각각 \(2\)와 \(3\)인 것을 제외하면 비슷해 보입니다만, 큰 차이점이 있습니다. 정수 \(k\)가 주어졌을때, 우리는 라그랑주 정리를 모르는 상태에서도 \((1)\)이 정수해를 가지는지의 여부를 유한한 시간 안에 알아낼 수 있습니다. 더해지는 제곱수 \(x^2\), \(y^2\), \(z^2\) , \(w^2\) 들이 각각 \(k\)보다 크면 안되는 이유로, 정수해 \((x,y,z,w)\)를 모두 찾으려면 콤팩트 지역에서 유한개의 후보들만 검사하면 되기 때문입니다. 반면 \((2)\)를 살펴보면, \(k\)가 주어졌을 때에 가능한 정수해 \((x,y,z)\) 의 크기에 대한 조건이 자명하지 않습니다. 실제로, \((2)\)의 정수해가 \(k\)에 비해서 상당히 큰 경우도 존재합니다. 예를 들어 우리는 \(34=(-1)^3+2^2+3^3\) 임은 쉽게 보일 수 있지만,\(33= (8,866,128,975,287,528)^3 + (-8,778,405,442,862,239)^3 + (-2,736,111,468,807,040)^3\)임은 찾기 쉽지 않습니다. 참고로, 위의 \(33\)에 대한 정수해는 영국의 수학자 부커 ^{Andrew Booker} 에 의해 2019년에서야 발견되었습니다.[2]

여기서 잠깐, 디오판토스 방정식을 일반적으로 풀 수 있는 방법이 있는지 물어볼 수 있습니다. 이 질문을 한 사람 중 20대 초반의 대 수학자 힐베르트^{David Hilbert} 가 있습니다. 1900년에 힐베르트는 다음의 문제를 프랑스 파리에서 열린 제 1회 대회 국제수학자대회에서 총 23개의 문제에 포함했습니다.

힐베르트의 열 번째 문제 (1900). 주어진 임의의 디오판토스 방정식이 정수해를 가지는지 여부를 판별하는 알고리즘을 찾으시오.

만약 위와 같은 알고리즘이 존재했다면, 앞서 언급 된 추측이 직접적으로 증명하지는 못하더라도 주어진 \(k\)에 대해 방정식 \((2)\)의 정수해 존재 여부를 알아내는 것은 시간 문제 이겠습니다. 그러나 힐베르트의 열 번째 문제는, 마티야세비치^{Yuri Vladimirovich Matiyasevich} 가 1970년 일반적인 알고리즘은 존재할 수 없다는 것을 증명함으로써 불가능함으로 일단락 되었습니다. 마티야세비치의 증명을 가볍게 설명하자면, 디오판토스 방정식을 이용하여 튜링 머신^{Turing machine} 즉 컴퓨터를 만들 수 있다는 것입니다! 튜링^{Alan Turing} 이 정지 문제의 일반적 해법이 없음을 증명하여, 계산 불가능한 정수 집합^{uncomputable set of integers} 의 존재가 이미 알려져 있었기 때문에, 이를 표현하는 디오판토스 방정식에 대한 해법 역시 존재하지 않음이 보입니다. 마티야세비치의 정리를 보다 자세하게 소개하는 글로는 [3]이 있습니다.

디오판토스 방정식의 일반적인 해법은 존재하지 않음이 알려졌지만, 그럼에도 불구하고 해법이 있는 방정식의 영역을 넓히는 수학자들의 여정은 계속됩니다. 방정식 (1)과 (2)의 두 예에서 살필 수 있듯이, 디오판토스 방정식의 연구에는 위상공간에 대한 다음 원칙이 중요한 역할을 합니다:

\begin{align*}
\tag{3} \textbf{Compact} + \textbf{Discrete} = \textbf{Finite.}
\end{align*}

예로 주어진 방정식을 만족하는 정수해들이 콤팩트 지역 안에 있거나, 특정한 변환을 통해 콤팩트 지역 안으로 보내질 수 있다는 것을 보이면, 정수해들의 유한성 또는 유한 생성성을 증명할 수 있는 것 입니다. 다음 두 장에서는, 위의 원칙을 살려서 우리가 풀고 연구할 수 있는 디오판토스 방정식의 두 가지 예를 살펴볼 것입니다. 다루어질 두 방정식의 공통점은, 각각이 특정한 수학적 물체들의 모듈라이 공간 (= 매개 변수화 하려는 물체들과 점들이 일대일 대응하는 다양체) 을 기술하며, 두 가지 속성을 가지게 된다는 것입니다:

• 매개화 되는 물체들의 자기 동형 사상군이 방정식의 대칭구조로 나타납니다.
• 매개화 되는 물체들이 수축량 부등식 등 미분기하 방법의 대상이 되고, 이것이 방정식의 풀이에 쓰입니다.

이 두 가지 속성은 정수해들의 유한 생성으로 귀결됩니다.

이항이차형식과 보형군

18세기부터 오일러^{Leonhard Euler}, 라그랑주, 르장드르^{Adrien-Marie Legendre}, 그리고 가우스^{Carl Friedrich Gauss} 같은 수학자들은 이차이항형식의 산술적 연구에 많은 힘을 쏟았습니다. 이차이항형식 (이하 “형식”) 이란 \(x^2+y^2\) 이나 \(3x^2+4xy-5y^2\) 같이 \(ax^2+bxy+cy^2\) 의 꼴로 나타내어지는 변수 \(x,y\)의 이차함수를 말합니다. 편의를 위해, 이 글에서 다뤄지는 형식 \(q(x,y)\) 은 전부 양의 정부호 형식임을, 즉 실수 쌍 \((x,y)\neq(0,0)\) 에 대해 \(q(x,y)>0\) 임을 가정하겠습니다. 정수 계수의 형식 \(q(x,y)\) 이 주어졌을때, 방정식 \(q(x,y)=k\) 에 대한 정수해 \((x,y)\) 가 존재할 경우, 형식 \(q\) 가 상수 \(k\) 를 “표현한다” 라고 정의합시다. 다음과 같은 문제를 생각할 수 있습니다.

질문. 형식 \(q(x,y)=1613x^2+254xy+10y^2\) 은 \(5\)를 표현하는가?

위와 같이 복잡한 계수를 가진 형식은, 때때로 보형군을 이용하여 더 간단한 형식 \(p(x,y)\)으로 변환할 수 있습니다. 여기서, 보형군^{modular group} 이란 다음의 행렬군을 의미합니다:

\(SL_2(\mathbb{Z})=\left\{g=\begin{bmatrix} a& b\\ c & d\end{bmatrix}:a,b,c,d\in\mathbb{Z},\det(g)=ad-bc=1\right\}.\)

보형군의 원소 \(g\) 가 있고 형식 \(q(x,y)\)가 있으면, 다음과 같은 작용을 통해 새로운 형식이 나옵니다:

\(\left(\begin{bmatrix} a& b\\ c & d\end{bmatrix}\cdot g\right)(x,y)=q(ax+cy,bx+dy)\)

예를 들어서, 위 질문에 언급된 형식 \(q(x,y)\)은 보다 간단한 \(p(x,y)=x^2+y^2\)으로 변환할수 있습니다. 따라서 \(q(x,y)\)와 \(p(x,y)\)가 표현하는 정수들의 집합은 서로 같으며, 특히 \(p(1,2)=1^2+2^2=5\) 이므로 \(q(x,y)\) 역시 \(5\)를 표현하는 것을 알 수 있습니다. 주목할 점은, 주어진 임의의 형식 \(q(x,y)=ax^2+bxy+cy^2\)의 판별식 \(Disc(q)=b^2-4ac\) 는 보형군의 작용에 대하여 불변이라는 것입니다. 따라서 판별식 값을 \(d\)로 가진 이차이항형식들의 모듈라이 공간을 계수 \(a,b,c\)에 대한 방정식으로 정의하면

\begin{align*}
\tag{4} F(a,b,c)=b^2-4ac=d
\end{align*}

이고, 이 모듈라이 공간에는 보형군의 선형 작용이 있음을 알 수 있습니다. 즉, 위 방정식의 정수해들의 구조를, 보형군의 작용을 이용하여 이해하는 것이 우리의 목표입니다. 다음은 라그랑주가 증명했습니다.

유한 생성 정리 1. \(d\neq0\)일때, \((4)\) 의 정수해 \((a,b,c)\) 들은 유한개의 보형군 궤도로 분류된다. 즉, 판별식 값이 \(d\)인 정수 이차이항형식의 보형군 궤도는 유한하다.

주어진 \(d\)에 대한 위의 보형군 궤도들의 집합을 \(Cl(d)\) 이라 합시다. 흥미롭게도, 이 유한 집합 \(Cl(d)\) 는 가우스가 발견한 합성 법칙에 의해 아벨군의 구조를 가지게 됩니다. 더 나아가 \(Cl(d)\)는 이차 체 \(\mathbb{Q}(\sqrt{d})\) 속의 특정 정수환의 아이디얼 유군^{ideal class group} 과 본질적으로 동형입니다. 후자는 주어진 정수환 내에서 산술의 기본 정리인 유일 인수 분해의 성립 여부를 결정하는, 정수론에서 중요하게 연구되어지는 군입니다. 그러한 이유로 위의 유한 정리는, 대수적 정수론의 시초를 상징하는 결과 중 하나라 할 수 있습니다.

다음 결과는 유한 생성 정리의 증명에 쓰이는 핵심 단계입니다.

짧은 곡선 정리 1. 실수 형식 \(q(x,y)\)가 주어졌을 때, 다음을 만족시키는 정수 쌍 \((x,y)\neq(0,0)\) 이 존재한다: \(q(x,y)\ll|Disc(q)|\).

여기서 \(\ll\) 부등호는 \(q\)에 의존하지 않는 상수가 함축되어 있음을 의미합니다. 위 정리는 \(2\)차원 민코프스키의 정리 를 이용하면 간단하게 얻을 수 있습니다. 참으로, 양의 정부호 형식 \(q(x,y)\) 가 주어졌을 때, 우리는 표준 놈^norm \(||(x,y)||=\sqrt{x^2+y^2}\) 이 주어진 공간 \(\mathbb{R}^2\)의 벡터 \(u,v\)를 적당히 골라

\(q(x,y)=||xu+yv||^2\)

의 꼴로 나타낼 수 있습니다. 벡터 \(u,v\) 가 생성하는 격자군 \(L\)으로 몫 \(T=\mathbb{R}^2/L\) 을 취하면, 이는 평평한 토러스를 정의합니다. \(L\)의 격자점 \((x,y)\) 들은 평평한 토러스 \(T\) 위의 닫힌 측지선^{closed geodesic} \(s_(x,y)\) 들과 일대일 대응이 되고, 다음을 보일 수 있습니다.

• \(2Area(T)=\sqrt{|Disc(q)|}\),
• \(Length(s_(x,y))=\sqrt{q(x,y)}\).

따라서, 위의 정리는 앞서 2장에서 언급되었던 수축량 정리의 일부입니다.

유한생성 정리 1의 증명. 위 짧은 곡선 정리 1 을 사용한 유한 생성 정리 1 의 증명을 간략하게 묘사하겠습니다. 먼저, 위 정리를 이용하면 \(q(x,y)\) 를 보형군의 작용을 통해 첫 계수 \(a\) 의 절대값이 \(|Disc(q)|\) 으로 통제되는 형식 \(q'(x,y)=ax^2+bxy+cy^2\) 으로 변환시킬 수 있습니다. 참으로, \(q(x,y)\)가 \(|Disc(q)|\)에 의해 통제되는 정수 쌍 \((x,y)\neq(0,0)\) 이 짧은 곡선 정리 1에 의해 주어졌을때, 이를 \((1,0)\) 으로 보내는 보형군의 원소가 항상 존재함을 보일 수 있고, 이 원소를 통해 변환된 형식은 언급된 성질을 가집니다. 즉 원칙 \((3)\) 으로 인해 새 형식 \(q’\)의 첫번째 계수의 값이 유한하게 정해지고, 또한 이때에

\(\left(\begin{bmatrix}1 & 0\\ \lambda & 1\end{bmatrix} \cdot q’\right)(x,y)=q'(x+\lambda y, y)=ax^2+(b+2a\lambda)xy+(c+b\lambda+a\lambda^2)y^2\)

꼴의 작용을 통해 두 번째와 세 번째 계수 역시 콤팩트한 지역으로 보낼 수 있습니다. 즉 모든 정수 형식 \(q(x,y)\) 는 보형군을 통해 콤팩트한 지역으로 보내지고, 이는 \((4)\)의 정수해들이 유한 개의 보형군 궤도로 나뉜다는 것을 의미합니다.

물론 라그랑주의 원래 증명은 방정식 \((4)\) 의 형태를 직접 이용한 것이었고, 민코프스키의 수의 기하학을 쓰지 않았습니다. 민코스프키 방법의 이점은, 판별 방정식 \(b^2-4ac=d\) 의 정수해의 구조를 넘어 다항 이차형식의 이해 및 일반적인 대수적 수체의 아이디얼 유군의 유한함 증명 등, 정수론의 다른 근본적인 결과들의 효과적인 증명을 가능케 하였다는 것입니다. (참고로 앞서 2장에서 언급 된 라그랑주의 네 제곱수 정리 역시 민코프스키의 정리를 이용하면 쉽게 증명할 수 있습니다.) 위와 같은 유한 생성 정리는, 민코스프키와 지겔^{Carl Ludwig Siegel} 뒤로 보렐과 하리시찬드라^{Borel and Harish-Chanrda} 에 의해 1962년 일반적인 산술군^{arithmetic group} 의 선형 작용에까지 확장되었습니다.[4]

마르코프의 방정식

앞선 3장에서는 평평한 토러스의 계량적인 기하학이 정수론의 고전적인 정리의 증명에 효과적으로 쓰임을 보았습니다. 더 일반적으로, 앞서 언급된 뢰브너의 정리나 그로모프의 수축량 부등식 역시, 디오판토스 방정식들의 해석에 쓸 수 있을까요? 한 예를 짧게 보이며 이 글을 마치도록 하겠습니다. 우선, 다음의 질문을 해보겠습니다.

질문. 다음의 행렬

\(A=\begin{bmatrix}2 & -1\\ -1 & 1\end{bmatrix}\)

은 보형군의 교환자commutator일까? 즉, \(XYX^{-1}Y^{-1}=A\) 를 만족시키는 보형군의 원소 \(X,Y \in SL_{2} (\mathbb{Z})\)는 존재할까?

물론 위의 \(A\)를 다른 보형군의 원소로 바꾸어서도 비슷한 질문을 할 수 있습니다. 위 질문은 변수 행렬 \(X\)와 \(Y\)의 계수들에 대한 디오판토스 방정식 문제라고 볼 수 있겠습니다. 3장에서 다룬 질문과는 달리, 위 방정식의 정수해는 콤팩트한 지역에 국한된다는 보장이 없기 때문에, 푸는 방법을 모르면 \(X\)와 \(Y\)의 가능한 값을 추측하는 방법 말고는 어떻게 접근해야 할 지 막막할 수도 있는 문제입니다.

일반적으로 보형군의 원소 \(X,Y,A\)로 이루어진 등식 \(XYX^{-1}Y^{-1}=A\) 에서 행렬 \(X,Y,XY\) 들의 대각합을 각각 \(x,y,z\) 이라 정하고, 주어진 행렬 \(A\)의 대각합을 \(k\) 이라고 하면, 다음과 같은 등식이 성립함을 보일 수 있습니다.

\begin{align*}
\tag{5} x^2+y^2+z^2-xyz-2=k.
\end{align*}

반대로, 위에 대한 등식을 만족시키는 정수해 \((x,y,z)\)가 존재할 경우, 이가 보형군에서 나오는 정수해인지 아닌지 판별하는 방법은 따로 있습니다. 따라서 위의 질문은 방정식 \((5)\)의 정수해에 관한 연구와 직결됩니다. 위 같은 디오판토스 방정식을 처음 연구한 이는 마르코프^{Andrey Andreyevich Markoff} 입니다. (마르코프의 1880년 연구는 이항이차형식의 근사, 황금률 등의 아름다운 주제를 다루었지만, 글이 너무 길어지게 되므로 설명을 생략하겠습니다.) 마르코프가 발견한 것은, 제 3 장에서 다루어진 판별 방정식 \(b^2-4ac=d\) 이 보형군의 작용을 지녔던 것처럼, 방정식 (5) 이 비선형 대칭군을 가지고 있다는 것입니다. 더 정확히, (5)는 다음의 사상들에 의해 보존됩니다:

• 변수들의 치환, \((x,y,z)\mapsto(y,x,z)\) 등.
• 비에타 대합^{Vieta involution} \((x,y,z)\mapsto(x,y,xy-z)\).

위의 사상들로 생성되는 군을 \(G\)라고 합시다. 마르코프의 방법을 쓰면, 위 사상들의 작용을 통해 (5)의 모든 정수해들을 콤팩트한 지역으로 보낼 수 있음을 증명 가능합니다. 즉, 다음이 보여집니다.

유한 생성 정리 2. \(k\neq2\) 일 때, \((5)\) 의 정수해 \((x,y,z)\) 들은 유한개의 \(G\) 궤도로 분류된다.

이 유한 생성 정리는 위의 질문에 대한 답을 가능하게 합니다. 우선 \((5)\)의 등식에서 \(k=3\)을 정하면, 마르코프의 방법을 통해 \((5)\)의 정수해 \((x,y,z)=(0,1,2)\)를 찾게 됩니다. 따라서 대각합의 조건을 만족시키는 행렬들을 계산하여 (유무의 판별과 계산법은 생략합니다.)

\(X=\begin{bmatrix}0 & -1 \\ 1 & 0\end{bmatrix},\quad Y=\begin{bmatrix}0 & 1 \\ -1 & 1\end{bmatrix},\quad A=\begin{bmatrix}2 & -1 \\ -1 & 1\end{bmatrix}\)

을 잡으면, \(XYX^{-1}Y^{-1}=A\) 를 만족시킴을 알 수 있습니다.

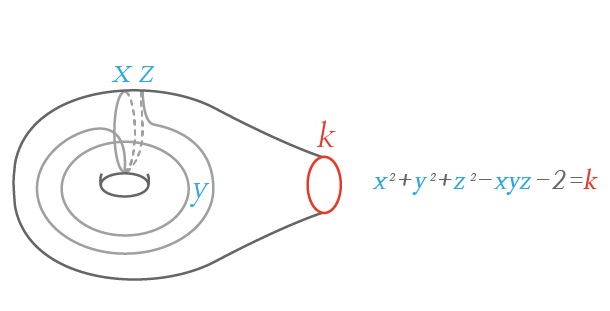
마르코프의 원래 증명은 위 대칭군 \(G\)의 작용과 \((5)\)를 직접 써서 얻어졌지만, 여기서는 조금 다른 접근법을 짧게 설명하겠습니다. 다소 기술적인 문단이 되지만, 결론적으로 1장에서 소개한 수축량 정리를 쓰기 위한 것임을 알려드립니다. 3장에서 방정식 \((4)\)를 이항이차형식의 모듈라이 공간으로 해석하여 정수해의 구조를 밝혀낸 것 같이, 방정식 \((5)\) 이 정의하는 대수적 다양체 역시 다음을 매개변수화 하는 모듈라이 공간으로 해석할 수 있습니다:

  종수 \(1\)이고 \(1\)개의 경계곡선이 있는 곡면 \(S\) 위
경계의 모노드로미 대각합이 \(k\)인 \(SL_2(\mathbb{C})\)-로컬 시스템.

예를 들어 두 개의 원소 \(X,Y \in SL_{2}(\mathbb{Z})\) 가 위처럼 주어졌을 때, 그에 상응하는 로컬 시스템은 곡면 \(S\)의 기본군^{fundamental group} 을 생성하는 정해진 두 개의 단일 폐곡선에 대한 모노드로미 원소가 각각 \(X,Y\) 인 로컬 시스템 이고, 따라서 \((x,y,z)\) 는 특정 단일 폐곡선들에 대한 로컬 시스템의 모노드로미 대각합을 의미합니다 [그림 3]. 위 모듈라이 공간에는 곡면 \(S\)의 매핑 클래스 그룹^{mapping class group} 이 작용하고, 이는 위에서 서술된 군 \(G\)의 작용과 본질적으로 같음을 보일 수 있습니다. 유한 생성 정리 1의 증명과 비슷하게, 유한 생성 정리 2 증명의 핵심 단계는 다음의 정리입니다.

짧은 곡선 정리 2. \(S\) 에 임의의 \(SL_2(\mathbb{C})\)-로컬 시스템 \(\rho\)이 주어졌을때, 다음을 만족시키는 \(S\) 위의 단일폐곡선 \(a\) 가 존재한다: \(|tr\rho(a)|\ll|tr\rho(\partial S)|\).

위의 정리는 주어진 로컬 시스템 \(\rho\)과 조화 사상^{harmonic map} 을 이용해 \(S\) 위의 적당한 리만 계량을 건설하고, \(S\)의 경계에 적당한 반구 표면을 붙여 리만 토러스 \(T\)를 만든 후, 뢰브너의 정리를 이용함으로써 증명됩니다. 유한 생성 정리 2를 이렇게 기하학적으로 증명하는 것의 이점은, 종수 \(g\)이고 \(n\)개의 경계곡선을 가진 임의의 곡면 상의 모듈라이 공간으로 쉽게 확장시킬 수 있다는 것입니다. 따라서 여러 곡면들의 사상류군이 가지는 비선형 작용에 대하여, 선형 산술군과 비슷하게도 정수점 유한 생성 정리가 성립이 된다는 것을 알 수 있습니다![5] 다음의 정리 역시 성립함을 보일 수 있습니다.[6]

정리. 보형군의 원소 \(A \in SL_{2}(\mathbb{Z})\) 와 자연수 \(g\geq1\)이 주어졌을 때. \(A\)가 보형군의 \(g\)개 교환자의 곱으로 나타내어지는지 아닌지 판별하는 알고리즘은 존재한다.

3장에서 살펴본 이항 이차형식의 산술은, 앞서 언급했듯이 현대 대수적 정수론의 기초가 되었습니다. 4장에서 이야기된 마르코프 방정식 (과 이를 포함한 일반적 곡면의 \(SL_2\)-로컬 시스템 모듈라이 공간) 의 정수해 유한 생성 정리의 깊은 산술적 의미에 대해서는, 아직 연구할 것이 많이 남아있다는 것이 필자의 의견입니다. 어떻게 보면 수학의 가장 기초적인 개념이라고 볼 수 있는 정수과 곡면, 이들 사이에 밀접한 관계가 있다는 건, 심장이 두근거리는 일이 아닐까요?