피타고라스는 세상의 모든 것이 정수의 비율로 나타난다고 믿었습니다. 전설에 따르면 \(\sqrt{2}\) 가 유리수가 아니라는 사실을 밝혀내고 그 존재를 누설한 그의 제자 히파수스를 죽이기까지 하였다고 합니다. 피타고라스의 입장에서는 아마도 변의 길이가 1인 정사각형은 너무 자연스러운 도형이기 때문에 이 정사각형의 대각선의 길이도 반드시 어떤 수로 나타낼 수 있어야 한다고 생각했을 것입니다. 그러나 그 당시 사람들에게 수란 정수의 비율로 나타낼 수 있는 유리수밖에 없었으므로 \(\sqrt{2}\) 가 수가 아니라는 사실은 수 체계에 대한 위기를 불러 일으켰습니다.1 19세기에 들어서 실수에 대한 엄밀한 정의가 완성되었지만 주어진 실수와 가까운 유리수를 찾으려는 시도는 예나 지금이나 자연스러운 것 같습니다. 이 글에서는 실수를 유리수로 근사하는 효과적인 방법과 관련된 내용에 대해서 알아보려고 합니다.
순정율과 평균율
모든 만물이 수라는 세계관을 가지고 있었던 피타고라스는 음악에서도 조화로운 정수의 비율을 찾고자 하였고 간단한 정수의 비를 이용한 음계이론을 구축하였습니다.
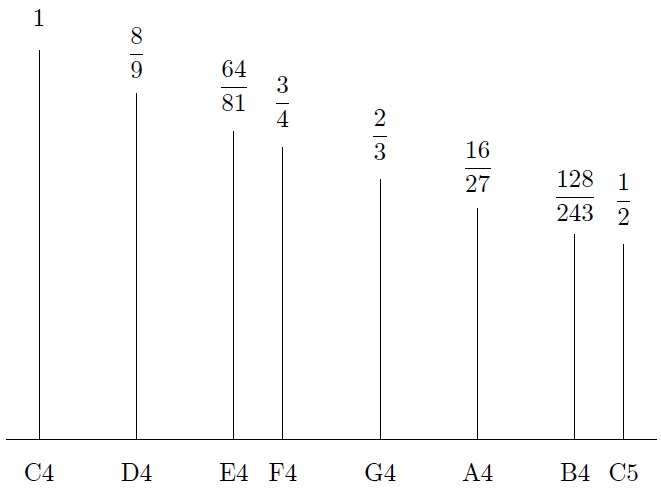
주어진 현에서 기준이 되는 도(C4)음이 난다고 할 때, 현의 길이를 절반으로 줄이면 진동수는 2배가 되며 이 때의 음은 1옥타브 높은 도(C5)가 됩니다. C4에서 현의 길이를 \(2/3\) 으로 줄이면 완전5도 높은 솔(G4)음을 얻고 C4에서 현의 길이를 \(3/4\) 로 줄이면 완전4도 높은 파(F4)음을 얻습니다. C4에서 현의 길이를 \(2/3\) 으로 줄인 후 다시 \(3/4\) 로 줄이면 처음 길이의 절반이 되어 “완전5도 \(+\) 완전4도 \(=\) 1옥타브” 라는 사실을 알 수 있습니다.옥타브와 완전5도, 완전4도를 기본으로 하여 나머지 음들의 현의 길이도 계산해볼 수 있습니다. 솔(G4)에서 완전5도를 높인 후 1옥타브 내리면 레(D4)가 되는데 이는 기준이 되는 도(C4)에서 현의 길이를 \(\frac{8}{9}\)배 한 것입니다. 이렇게 얻은 7개의 길이에서 A4,E4,B4의 \(\frac{16}{27},\frac{64}{81},\frac{128}{243}\) 대신에 이와 가까운 \(\frac{3}{5},\frac{4}{5},\frac{8}{15}\) 를 사용하여 얻은 음계를 ‘순정율pure temperament’이라고 부릅니다.
간단한 분수들로 이루어진 순정율은 아름답지만 안타까운 모순을 가지고 있습니다. 피아노 건반에서 가장 낮은 도음 C1에서 출발하여 가장 높은 도음 C8에 도착할 때, 한 옥타브씩 일곱 번 증가하여 도착한 것과 완전5도씩 열두 번 증가하여 도착한 것이 같아야 하는데 이 관계를 주파수의 비율을 사용하여 나타내면
\(2^7=\left(\frac{3}{2}\right)^{12}\)
가 되어
\(2^{19}=3^{12}\)
를 얻습니다. 분명히 좌변은 짝수이고 우변은 홀수이므로 이는 분명 이상합니다. 피타고라스와 그 학파들의 음악 이론은 이렇게 불완전한 부분이 있었고 그로 인하여 한 옥타브 사이에 열 두 음을 고르게 놓아야 한다는 이론이 등장했습니다. 즉, 주파수가 일정한 비율로 열 두 번 증가하여 2배가 되기 위해서는 각 단계마다 \(2^{\frac{1}{12}}\) 의 비율로 증가해야 한다는 사실을 토대로 음고를 정한 것을 평균율이라고 합니다.2그런데 왜 하필 열 두 번일까요?
최선의 유리수 근사를 찾는 법
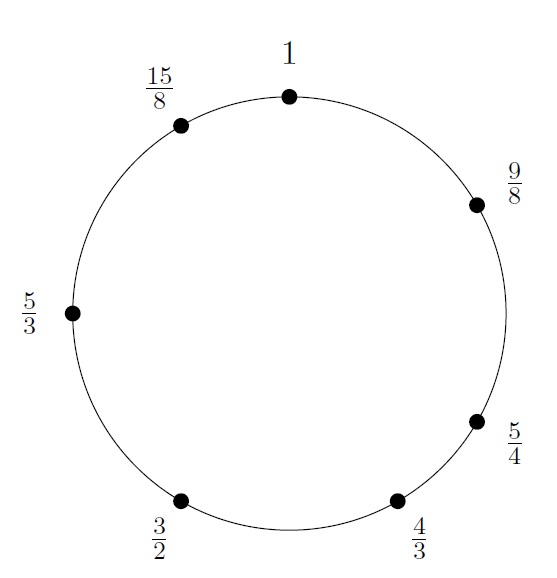
한 변의 길이가 1인 정사각형의 대각선 길이인 \(\sqrt{2}\)는 평균율의 도음 C와 F# 사이의 주파수 비율이기도 합니다. 아래 표를 보면 평균율과 순정율이 완전히 같지는 않더라도 꽤 비슷하게 움직인다는 것을 알 수 있습니다.
예를 들어 \(2^{\frac{7}{12}}\) 와 \(\frac{3}{2}\) 은 꽤 가까운 수가 되는데,여기서 \(\frac{7}{12}\) 이라는 분수를 어떻게 찾을 수 있었을까요? \(2^\square\) 가 약 \(\frac{3}{2}\) 이 되는 유리수 \(\square\) 를 찾는 문제는 양변에 밑을 2로 하는 로그를 적용하면 \(\log_2\frac{3}{2}\) 와 가까운 유리수를 찾는 문제가 됩니다. 물론 \(\log_2\frac{3}{2}\) 을 컴퓨터로 계산하면 \(0.5849625007211\ldots\) 이므로
\(\frac{5}{10}, \frac{58}{100}, \frac{584}{1000},\frac{5849}{10000},\frac{58496}{100000},\ldots\)
가 \(\log_2\frac{3}{2}\) 에 점점 가까워지는 유리수들이 되기는 합니다. 하지만 우리는 \(\frac{58}{100}\left(=\frac{29}{50}\right)\) 같은 분수보다는 분모가 작으면서도 나름 정확도는 높은 유리수들을 찾고 싶습니다.3
좋은 근사를 찾는 법은 근본적으로 다음의 네모 채우기 놀이(=연분수 표현)에서 나옵니다.4 가로와 세로의 비율이 \(x:1\) 인 직사각형을 생각하고 남은 공간에 들어갈 수 있는 가장 큰 정사각형을 왼쪽에서부터 혹은 아래에서부터 최대한 많이 채워나간다는 규칙대로 직사각형을 채워나가봅시다. 이 과정을 충분히 반복하면 실수 \(x\) 와 가까운 유리수들을 알아낼 수 있습니다. 정사각형을 왼쪽에서 \(a_0\)번, 아래쪽에서 \(a_1\)번, 다시 왼쪽에서 \(a_2\)번, 아래쪽에서 \(a_3\)번 채워나갈 수 있을 때 그 횟수를 순서대로 기록하여
\(x=[a_0;a_1,a_2,a_3,\ldots]\)
로 쓴다면,5 다음의 유리수들이 \(x\) 를 가장 최선의 방법으로 근사한다는 사실이 알려져 있습니다.
\(a_0+\dfrac{1}{a_1},a_0+\dfrac{1}{a_1+\dfrac{1}{a_2}},a_0+\dfrac{1}{a_1+\dfrac{1}{a_2+\dfrac{1}{a_3}}},\ldots\)
기약분수 \(\frac{p}{q}\) 가 \(x\) 를 최선의 방법으로 근사best approximation한다는 것은 분모가 \(q\) 보다 작거나 같은 기약분수 중에서 \(\frac{p}{q}\) 보다 \(x\) 에 더 가까운 것은 없다는 이야기입니다. 앞서 궁금했던 \(x=\log_2{\frac{3}{2}}\) 의 경우 위의 규칙대로 진행하면
\(\log_2{\frac{3}{2}}=[0,1,1,2,2,3,\ldots]\)
가 되어 \(\log_2\frac{3}{2}\) 을 “가장 잘 근사하는” 유리수열은
\(1,\frac{1}{2},\frac{3}{5},\frac{7}{12},\,\frac{24}{41},\,\frac{31}{53},\,\frac{179}{306},\,\frac{389}{665},\ldots\)
이 되겠습니다. 여기서 \(\frac{3}{5}\) 이나 \(\frac{7}{12}\) 이 포함되어 있는 것을 보면 왜 우리가 5음계나 12음계를 주로 사용해왔는지 알 수 있습니다.만약 12음계보다 더 분할하여 음악 이론을 전개하고 싶다면 27음계나 35음계가 아닌 41음계를 사용하는 것이 좋겠습니다. 다만 옥타브가 아닌 완전 5도를 동일하게 분할하자는 아이디어에서 출발하여 완전 5도를 20등분한 경우도 있다고 합니다.6
잘 근사되지 않는 실수
주어진 실수 \(x\) 를 최선의 방법으로 근사하는 유리수를 찾는 법을 알았습니다. 이제 그 최선의 근사가 얼마나 효율적인지 혹은 그렇지 않은지 알아보고자 합니다. 주어진 실수 \(x\) 에 대해 \(x\) 를 넘지 않는 가장 큰 정수를 \([x]\) 라 쓰고 \(x-[x]\) 를 \(\{x\}\) 로 쓰겠습니다. 예를 들어, \([7.6]=7\), \(\{7.6\}=0.6\) 이고 \([-2.9]=-3\), \([-2.9]=0.1\)이 되겠습니다.
1842년에 수학자 디리클레Dirichlet는 임의의 실수 \(x\) 와 1보다 큰 실수 \(Q\) 에 대해 \(\left|qx-p\right|<\frac{1}{Q}\) 이면서 \(1\le q\le Q\) 를 만족하는 정수 \(p,q\) 가 존재한다는 사실을 증명하였습니다.7 이 사실로부터 임의의 실수 \(x\) 에 대해
\(\left|x-\frac{p}{q}\right|<\frac{1}{q^2}\)
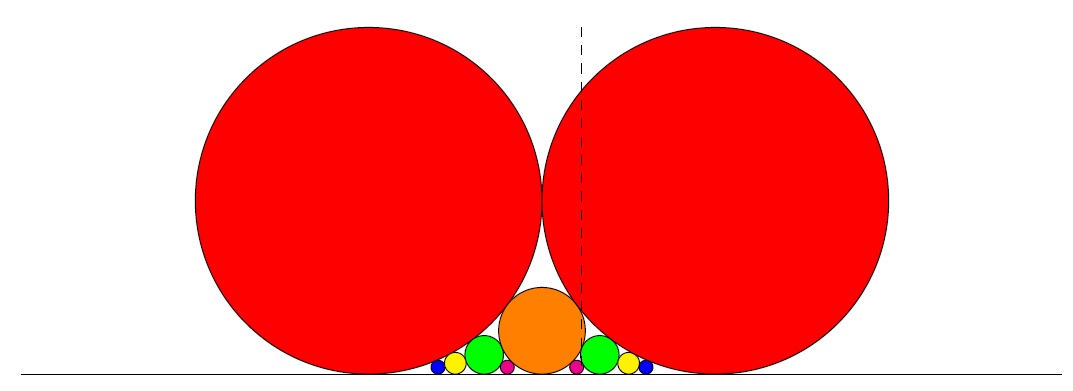
을 만족하는 정수 \(p,q\) 가 반드시 존재함을 알 수 있습니다. 특별히 \(x\) 가 무리수인 경우에는 위의 조건을 만족하는 정수가 무한히 많다는 사실을 포드Ford의 원이라 부르는 다음의 그림을 통하여 알 수 있습니다.8
실직선 위의 두 점 0과 1에 접하는 반지름이 \(\frac{1}{2}\) 인 두 원을 먼저 그립니다. 이제 두 원 사이에서 접하면서 실직선에 동시에 접하는 원을 점점 그려나갑니다.이 과정을 반복하면 0과 1사이의 모든 분수마다 그 점에서 접하는 원을 얻게 됩니다.9 약간의 계산을 통하여 모든 기약분수 \(\frac{p}{q}\) 마다 그 점에 접하는 반지름이 \(\frac{1}{2q^2}\) 인 원이 그려짐을 알 수 있습니다. 포드의 원에서 \(x\) 가 무리수인 경우 \(x\) 에서 수직으로 뻗은 점선을 그리면 이는 무한히 많은 원과 만나므로 다음의 부등식
\(\left|x-\frac{p}{q}\right|<\frac{1}{2q^2}\)
이 무한히 많은 유리수 \(\frac{p}{q}\) 에 대해 성립합니다. 더 나아가서 실은
\(\left|x-\frac{p}{q}\right|<\frac{1}{\sqrt{5}q^2}\)
을 만족하는 유리수가 무한히 많다는 사실을 휴르비츠Hurwitz가 1891년에 증명하였습니다.10 그런데 여기서 \(\sqrt{5}\) 를 더 큰 실수로 바꾸면 주어진 명제는 성립하지 않게 됩니다. 예를 들어, 황금비로 잘 알려진 \(\rho=\frac{1+\sqrt{5}}{2}\) 인 경우 \(\sqrt{5}\) 보다 큰 \(L\) 에 대해서는
\(\left|\rho-\frac{p}{q}\right|<\frac{1}{Lq^2}\)
를 만족하는 서로소인 정수의 순서쌍 \((p,q)\) 이 유한 개 뿐입니다. 이와 같이 \(\left|x-\frac{p}{q}\right|<\frac{1}{L(x)q^2}\) 를 만족하는 서로소인 정수의 순서쌍 \((p,q)\) 가 유한 개 뿐인 \(L(x)\) 가 존재하는 경우 \(x\) 를 잘 근사되지 않는 실수badly approximable number라고 말합니다. 위 부등식의 해의 개수에 대한 무한과 유한 여부의 기준이 되는 \(L(x)\) 로 나타나는 값들을 라그랑즈 스펙트럼Lagrange spectrum이라고 말하는데11 이 값들은 가장 작은 \(\sqrt{5}\) 에서 출발하여 적어도 \(3\) 까지는 띄엄띄엄 나타난다는 사실을 마르코프Markoff가 1879년에 증명하였습니다. 라그랑즈 스펙트럼은 3부터 프레이만 상수Freiman’s constant라 부르는 곳12까지는 복잡한 형태를 띄다가 그 이후부터 연속적으로 나타나는 신기한 성질을 가지고 있습니다. 가장 작은 라그랑즈 스펙트럼을 갖는 황금비는 어떤 의미에서 가장 잘 근사되지 않는 실수라고 볼 수 있겠습니다.13
디오판토스 근사의 응용
만약 주어진 실수 \(x\) 에 대해
\(\left|x-\frac{p}{q}\right|<\frac{1}{q^{100}}\)
을 만족하는 서로소인 정수쌍 \((p,q)\) 가 무한히 많다면 \(x\) 는 꽤 잘 근사되는 실수처럼 보입니다. 오른쪽 항의 분모의 지수를 100 대신 10000 으로 바꿀 수 있으면 정말 잘 근사가 되는 수라는 느낌이 듭니다. 아예 10000 대신 임의의 큰 수를 넣어도 조건을 만족한다면 \(x\) 는 “거의 유리수같은 수almost rational number“라고 봐도 괜찮을 듯 합니다. 그런데 \(\sqrt{2}\), \(\frac{1+\sqrt[3]{5}}{4}\), \(\sqrt[4]{6}+\sqrt[5]{7}\) 같이 어떤 다항식의 근으로 나타나는 수들은 이렇게 잘 근사되지는 않는다는 사실이 알려져 있습니다. 리우빌Liouville은 1844년에 “거의 유리수같은 수”들은 다항식의 근으로 나타나지 않는다는 사실을 밝혀 초월수transcendental number14에 대한 이론을 발전시키는데 많은 공헌을 하였습니다. 리우빌의 관찰은 튜Thue, 지겔Siegel, 로쓰Roth에 의해 순차적으로 일반화되어 현재 튜-지겔-로쓰 정리로 불리고 있습니다. 이를 요약하면 “꽤 잘 근사되는 실수” 역시 다항식의 근으로 나타나지 않는다는 것으로 볼 수 있습니다.
정리1 (Thue-Siegel-Roth 1909년\(\to\)1921년\(\to\)1955년). \(x\) 가 어떤 다항식의 근으로 나타나는 실수인 경우 임의의 양수 \(\epsilon>0\) 에 대해
\(\left|x-\frac{p}{q}\right|<\frac{1}{q^{2+\epsilon}}\)
을 만족하는 서로소인 정수쌍 \((p,q)\) 는 유한하다.
실수의 유리수 근사(디오판토스 근사)는 디오판토스 방정식의 해를 구하는데도 응용이 가능합니다. 다음과 같은 방정식 \(x^3-2y^3=10\) 의 정수해는 얼마나 많이 있을까요? 먼저 \((2,-1)\) 이나 \((4,3)\) 을 떠올릴 수 있습니다. 이 외에 다른 정수해가 또 있는지는 확인을 해보아야겠지만 \(\sqrt[3]{2}\) 의 유리수 근사를 이용하여 적어도 해의 개수가 유한하다는 것을 알 수 있는 방법이 있습니다. 위의 튜-지겔-로쓰 정리에 따르면
\(\left|\sqrt[3]{2}-\frac{p}{q}\right|\ge \frac{c}{q^{5/2}}\)
을 만족하는 실수 \(c\) 가 존재합니다. 실제로
\(\left|\sqrt[3]{2}-\frac{p}{q}\right|\ge \frac{1}{4q^{5/2}}\)
가 모든 서로소인 \(p,q\) 에 대해 성립한다는 사실을 이용하면 \(|x^3-2y^3|\ge\sqrt{|y|}\) 가 위 방정식의 해 \((x,y)\) 에 대해 항상 성립함을 알 수 있습니다. 따라서 \(|y|\le 100\) 인 경우에만 위의 방정식을 확인해보면 되겠습니다.15
최근에는 실수를 유리수로 근사하는 것을 넘어서 여러 개의 실수를 같은 분모를 갖는 유리수로 동시에 근사하는 것, 대수적 다양체 위의 일반적인 점을 유리점으로 근사하는 것, 순서를 갖지 않는 다른 완비성을 지닌 체에서의 디오판토스 근사 등을 수학자들이 연구합니다.이 과정에서 디오판토스 근사 이론과 다른 분야의 최신 이론 사이의 다양한 연관성이 발견되었습니다.16,17 그러나 단순해보이는 실수의 유리수 근사에서도 아직 모르는 부분이 많은 것이사실입니다. 예를 들어, \(\sqrt[3]{2}\) 가 잘 근사되지 않는 수인지 그 여부 역시 아직 알려지 있지 않습니다.
맺음말
더 다루고 싶은 내용이 많지만 이쯤에서 필자의 엉터리 철학으로 글을 마무리하려고 합니다. 주어진 실수의 최적의 근사는 우리에게 익숙한 십진법 전개가 아니라 어쩌면 더 자연스러운 표현일지도 모르는 연분수 전개에서 나왔습니다. 황금비 상수는 분명히 자연의 다양한 곳에 아름다운 모습으로 내재되어 있지만 적어도 피타고라스의 관점에서는 가장 아름답지 않은 소리일지도 모릅니다. 익숙함에 속아 소중한 것을 잃지 말고 획일화된 아름다움의 기준에 얽매이지 말아야 겠습니다.