[2월의 퍼즐 해설] 뾰족한 별팔면체의 전개도

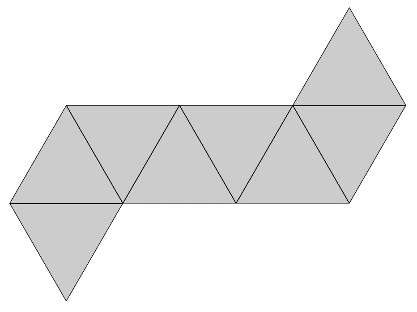
쉽게 생각하기 위해 정팔면체를 펼쳐 전개도를 그린 후, 전개도의 각 정삼각형 위에 삼각뿔을 붙인 다음, 다시 그것을 펼쳐서 최종 전개도를 얻는 식으로 접근해 보자. 먼저 아무 정팔면체의 전개도를 가져오자.

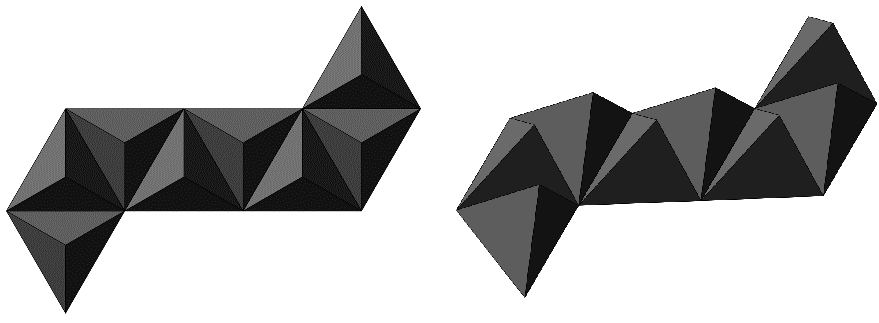
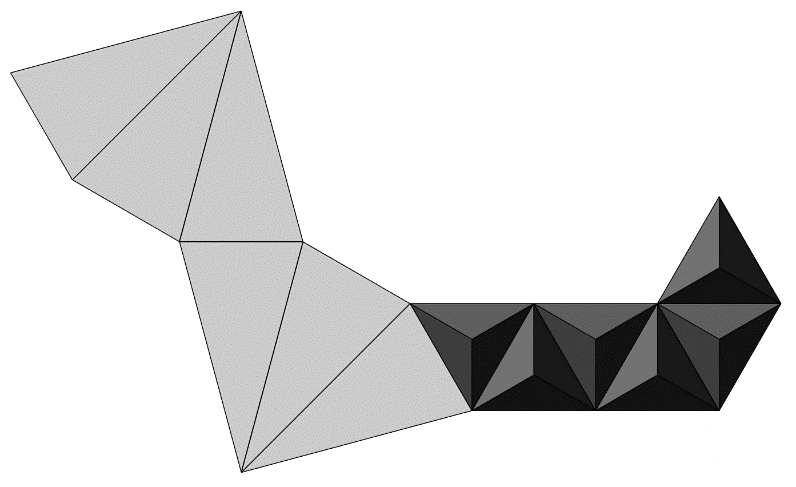
그리고 각 정삼각형을 밑면이 없는 삼각뿔로 치환하면 아래와 같이 된다. 이 도형은 뾰족한 별팔면체를 부분적으로 펼친 것이다. 위에서 바라보면 왼쪽, 살짝 옆에서 바라보면 오른쪽 그림과 같이 보인다.

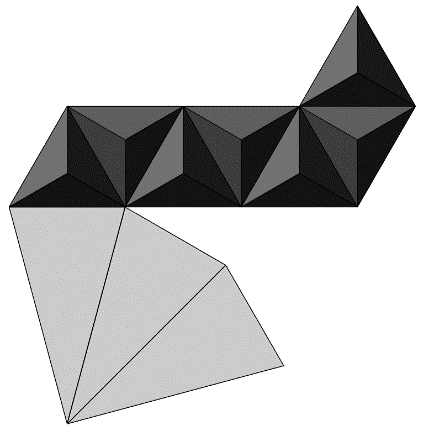
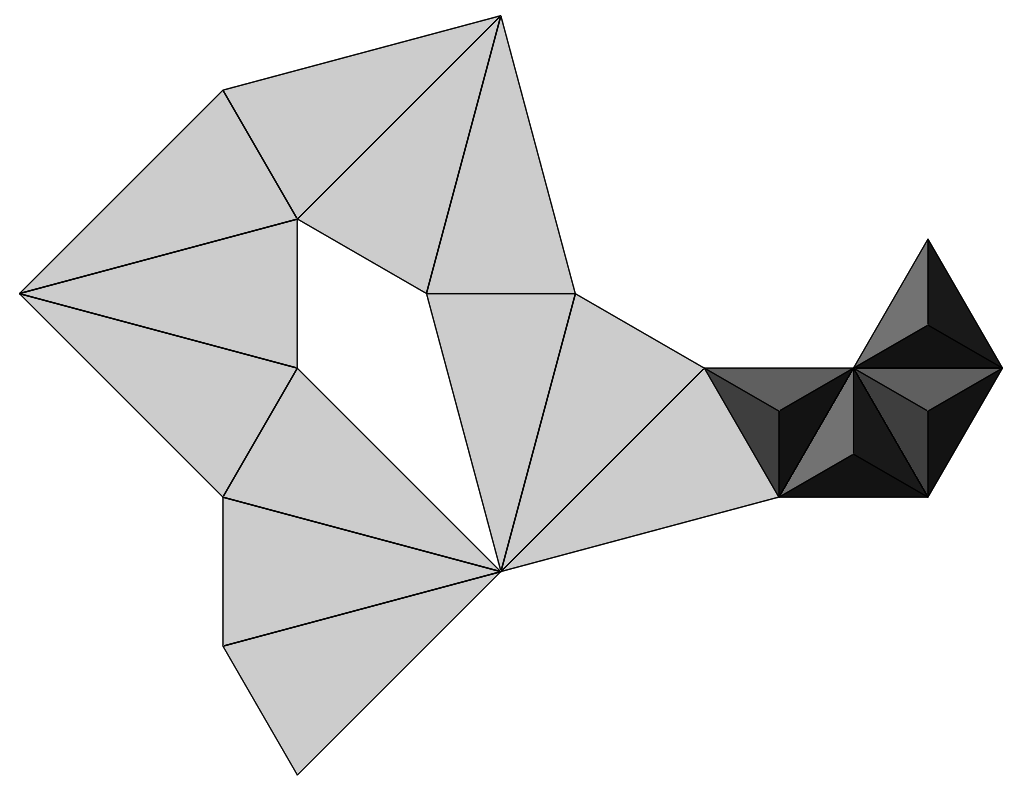
왼쪽 아래의 삼각뿔 한 개만 펼쳐 보자. 세 가지 방법으로 펼칠 수 있겠으나 예를 들어 보겠다.

삼각뿔을 펼쳐서 부채꼴이 되었다. 하나를 더 펼쳐 보자. 이것도 물론 세 가지 방법으로 펼칠 수 있지만 예를 들어 보겠다.

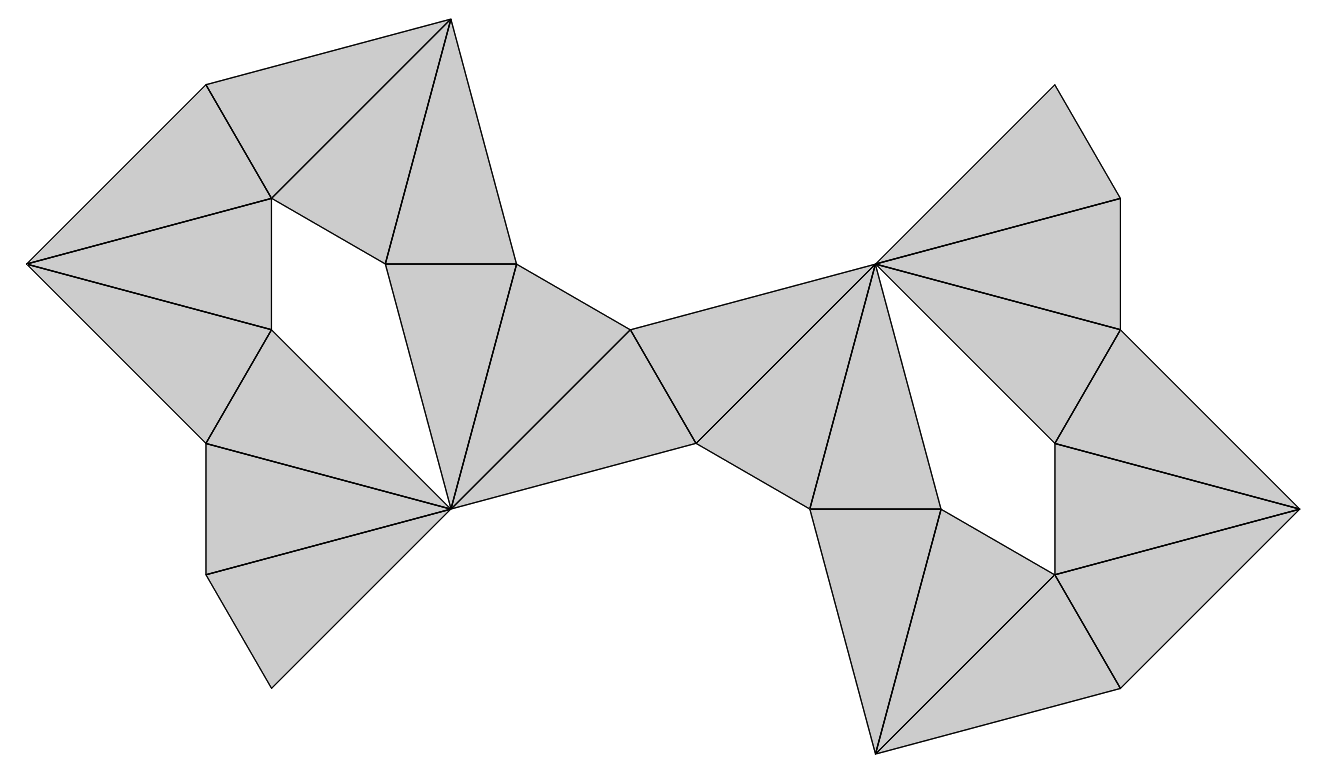
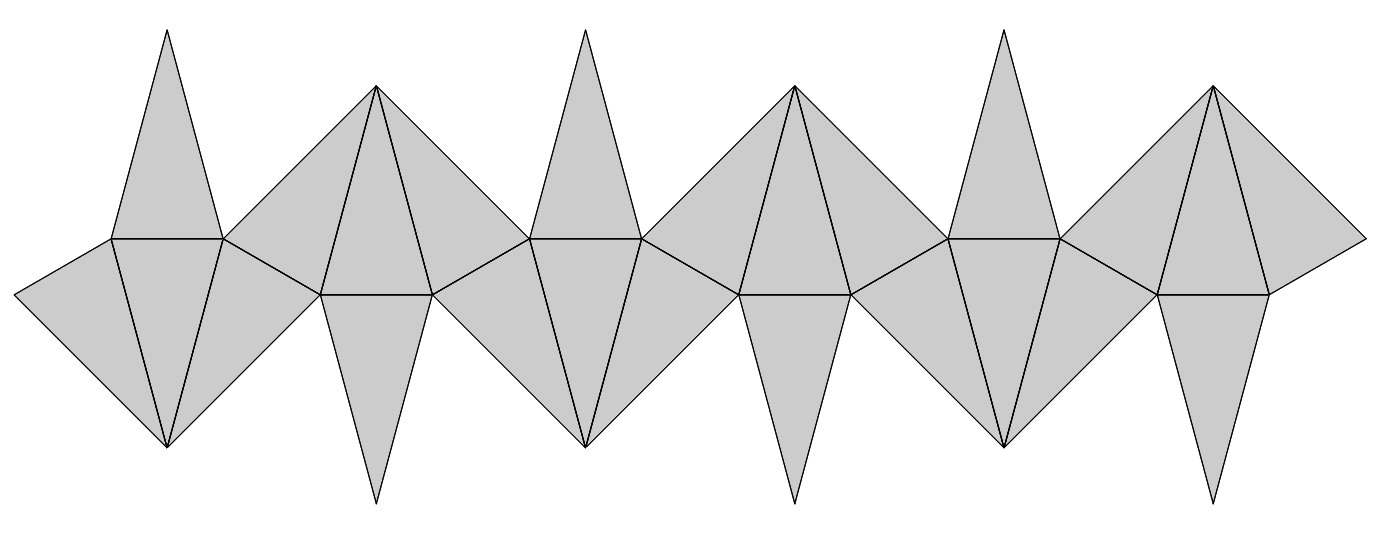
이렇게 8개의 삼각뿔을 하나하나 펼치면 부채꼴 8개가 서로 밑면을 맞대고 붙어 있는 모양의 전개도가 될 것이고, 그 전개도가 자기 자신과 겹치지 않으면 정답이다. 2개를 더 펼쳐 보자.

전개도가 자기 자신과 한 점에서 정확히 맞닿는 것을 볼 수 있다. 나머지는 대칭적으로 펼치면 된다.

물론 처음에 선택한 정팔면체의 전개도와 그것을 펼치는 방법에 따라 다른 답도 많이 존재한다.

보너스 퀴즈: 더 뾰족한 별팔면체의 전개도

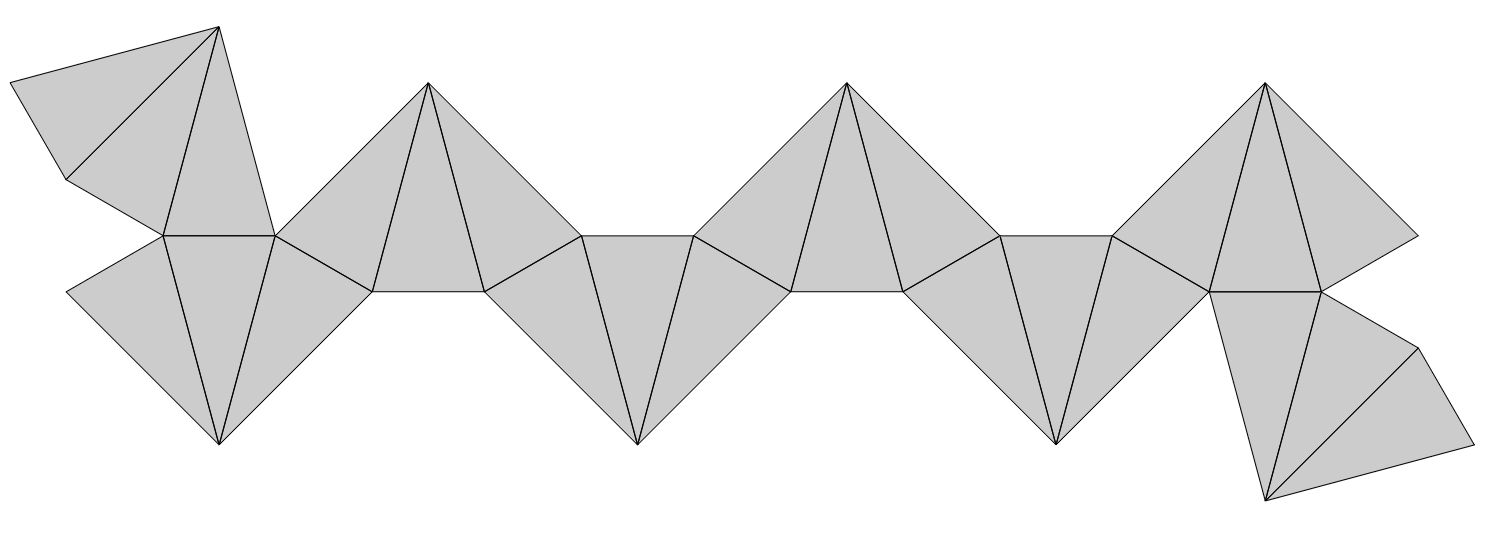
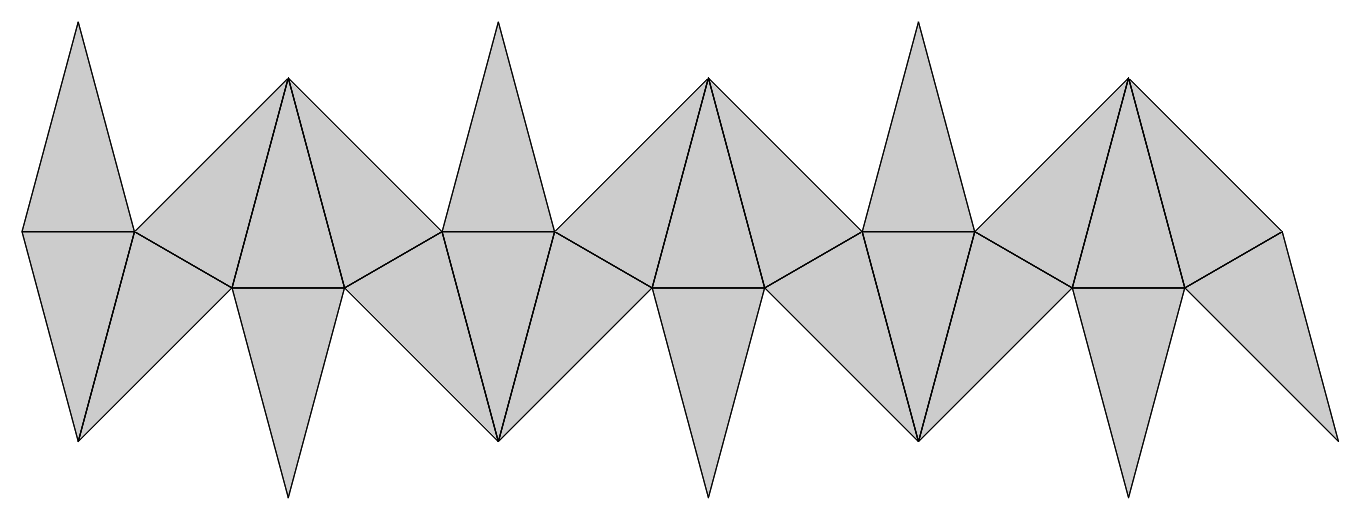
위 전개도는 이등변삼각형의 꼭짓각이 30도 미만이면, 즉 별팔면체가 더 뾰족해지면 자기 자신과 겹치게 된다. 이 문제를 해결하는 데에는 여러 가지 방법이 있겠으나, 앞서 구한 정답을 조금 변형하여 만드는 것이 가장 간단한 방법일 것이다. (앞에서 구한 전개도의 모양에 따라서 변형이 쉽게 되지 않을 수도 있다.) 양쪽 끝의 두 삼각뿔들을 다르게 펼치면 아래와 같은 답을 얻을 수 있다.

물론 이것도 훌륭한 정답이지만, 여기서 조금만 더 변형하면 더욱 대칭적인 답이 나온다. 출제자의 마음에 가장 마음에 드는 전개도는 다음 두 가지다. 예쁘지 않은가?