혼돈과 불변이 공존하는 역학계

1. 동역학계^{Dynamical systems}

동역학계^{Dynamical systems}는 무슨 학문인가? 간단하게 표현하자면, 주어진 (위상, 확률, 거리 등) 공간 \(X\)와 사상 \(f\colon X \to X\) 혹은 흐름 \(f_t \colon X \to X\)의 진화를 연구하는 학문이다. 두 종류의 변환을 통틀어서 동역학계라 부르며, 쉬운 이해를 위해서 이 글에선 연속적인^continuous 역학계보다는 이산적^discrete 역학계에 초점을 맞추었다. 하나의 시간의 단위가 흘러갈 때 공간 \(X\)가 한 번의 \(f\)에 의해 변형된다고 가정하면, 여기서 진화란 많은 시간이 흘렀을 때 \(X\)가

\(f^n:= \underbrace{f \circ \ldots \circ f}_{n}\)

의해 어떻게 변형하는지를 뜻한다.이러한 진화를 연구하는 데 있어 여러 가지 방법이 존재하는데, 그중에는 어떤 특정한 점 \(x\in X\)의 \(f\)-궤도 \(\{f^nx\}_{n\in N}\)의 (혹은 \(f\)가 가역 변환일 때는 \(\{f^nx\}_{n\in Z}\)) 행동을 연구하기도 하며, \(f\)에 관한 보존측도¹ \(\mu\)를 하나 선택 후 그 측도에 관한 대부분 점들의 궤도를 해석학의 관점에서 연구하는 방법도 있다. 또 다른 방법으로는 \(f\)가 작은 섭동\(^{\text{perturbation}}\)에 의해서 어떻게 변하는지 연구하기도 하며, 이 글의 주제 중 하나인 카오스\(^{\text{chaos}}\)와 연관되며 역학계의 복잡도를 나타내는 위상학적 엔트로피 \(h_{top}(f)\)를 통해서 \(f\)에 관한 정보를 얻기도 한다.

카오스 한글로 직역하면 “혼돈”, 즉 질서가 없다는 뜻을 의미한다. 동역학계에 관한 이 글에선, 아래 더 자세하게 살펴볼 균등한 쌍곡성질과 그에 연관되는 성질들을 포괄적으로 카오스라 일컬으려 한다. 예시를 하나 들자면, 쌍곡성질을 가지는 역학계는 공간 위에 다른 두 점 \(x,y \in X\)이 주어졌을 때, 처음 두 점이 얼마나 가깝던지 상관없이 시간이 충분히 흘렀을 때² 두 점의 궤도가 대폭 달라진다. 즉, 카오스 성질을 가진 역학계는 시작점의 작은 변화가 먼 미래 혹은 과거에 예측할 수 없는 변화를 가져온다고 볼 수 있다. 이러한 면에서 카오스를 직역한 “혼돈”과 비슷한 부분이 있다. 하지만 반대로 이런 역학계들은 카오스 성질에 의해서 전체적인 구조가 보존되는 성질도 가진다. 혼돈과 불변이 공존하는 역학계가 존재한다는 게 흥미롭지 않은가? 이 글에선 이런 역학계들에 대해 더 자세하게 알아보려 한다.

동역학계 정의에서도 알 수 있듯이 그 범주가 워낙 넓어서, 수학의 어느 분야에서나 역학계를 쉽게 찾아볼 수 있으며, 넓은 스펙트럼의 다양한 역학계가 존재한다. 카오스 성질에 얼마나 가까운지를 기준으로 다양한 역학계들을 스펙트럼에 나열했을 때, 스펙트럼의 한쪽 끝에는 원 \(\mathbb{S}^1 = \mathbb{R} /\mathbb{Z}\)위의 회전 \(R_a \colon \mathbb{S}^1 \to \mathbb{S}^1\)과 같은 보다 “단순”한 역학계들이 있다.여기서 “단순”하다는 표현을 사용하지만, 여기 포함되는 역학계들이 흥미롭지 않다는 뜻은 아니다.예를 들면 \(a\)가 무리수일 때, 무리각 회전 \(R_a \colon \mathbb{S}^1 \to \mathbb{S}^1\)은 유일한 보존측도를 가지고 있기 때문에 강한 에르고딕 성질³을 가지고 있으며, 얼마나 \(a\)가 유리수에 가까운지에 따라서^{well approximated by rationals} 서로 다른 성질을 보이기도 한다. 따라서 “단순”한 역학계란 그저 아래 소개할 카오스와 연관되는 다른 역학계에 비해서 단순하다는 뜻이다.

스펙트럼의 반대쪽 끝엔, 카오스와 연관 지어 볼 수 있는 균등한 쌍곡성질^{uniform hyperbolicity}을 가지는 역학계가 존재하며, 이 중에는 아래에서 조금 더 자세하게 살펴볼 Arnold’s cat map도 포함된다.

스펙트럼의 양쪽 끝에 자리 잡고 있는 두 종류의 역학계 외에도, 스펙트럼 중간에 흥미로운 성질을 갖는 여러 가지 역학계가 존재한다. 몇 가지 예시를 들자면, 균등한 쌍곡성질과 그에 반대되는 성질이 공존하는 역학계들도 즐비하게 존재하며, 공간의 대부분에선 쌍곡성질을 띄지만 쌍곡상수가 균등하지 않으며 특정한 부분 공간에는 쌍곡성질이 퇴화하는 역학계도 존재한다. 또한 여러 가지 방법을 사용하여 이미 존재하는 역학계들로부터 흥미로운 성질을 가지는 여러 가지 새로운 역학계를 만들기도 한다.

아래 본문에서는 먼저 중요한 예시인 Arnold’s cat map을 살펴보며, 균등한 쌍곡성질을 가지는 역학계에 대해 더 자세하게 알아보려고 한다. 그 후에는, 카오스와 연관되는 또 다른 개념인 위상학적 엔트로피 \(h_{top}(f)\)를 설명하고, 동역학계를 연구하는 데 있어 그 쓰임새를 알아보려고 한다.

2. 균등한 쌍곡성질의 동역학계

(1) 아놀드의 고양이 변환^{Arnold’s cat map}

균등한 쌍곡성질을 정의하기에 앞서, 특정한 예시를 하나 살펴보겠다.
가역행렬 \(A = \begin{pmatrix}
2 & 1 \\
1 & 1
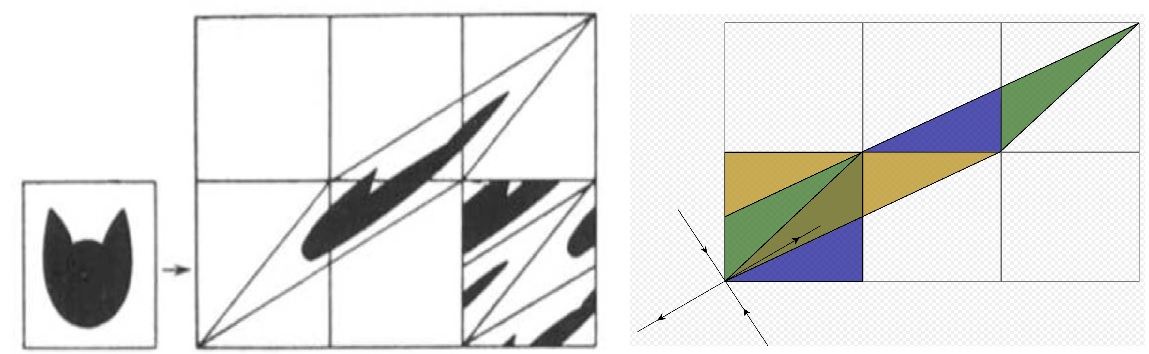
\end{pmatrix} \in \text{SL}_2(Z)\)를 고려해 봤을 때, 이 행렬은 두 개의 실고유값 \(\displaystyle\lambda_+ = \frac{3+\sqrt{5}}{2} >1\)과 \(\displaystyle\lambda_- = \frac{3-\sqrt{5}}{2} <1\)를 가지고 있으며, 각 고유값에 해당하는 고유벡터를 \(v_+\)와 \(v_-\)로 표기하겠다.2차원 벡터공간 \(\mathbb{R}^2\)에 대한 \(A\)의 선형 변환을 \(L_A \colon \mathbb{R}^2 \to \mathbb{R}^2\)라 표기하면, \(\mathbb{R}^2\)의 몫공간인 2차원 원환면^2-torus \(T^2:=\mathbb{R}^2/\mathbb{Z}^2\)에 대해 \(L_A\)는 그에 해당하는 변환을 정의한다. 이 변환을 학계에서는 수학자 Vladimir Arnold의 이름을 따서 Arnold’s cat map이라 부르며, 이 글에선 \(f_A \colon T^2 \to T^2\)로 표기하겠다. 수식으로는

\(f_A(x,y) = (2x+y,x+y) \mod 1\)

으로 쓰여지며, 원환면 \(T^2\)가 \(f_A\)에 의해 어떻게 변형하는지는 아래 [그림1]로 잘 설명된다.

Arnold’s cat map은 선형변환이기 때문에, 모든 점 \(x \in T^2\)의 국소적 근방은 \(f_A\)에 의해 \(v_+\) 방향으로 확대되며 \(v_-\) 방향으로 축약된다; \(x\) 근방의 원판이 \(f_A(x)\) 근방에 \(v_+\)를 장축으로 (그리고 \(v_-\)를 단축으로) 가지는 타원으로 변형되는 걸 생각하면 이해에 도움이 될 것이다. 특히 \(f_A\)의 유일한 부동점^{fixed point}인 원점^origin의 근방을 지나는 \(f_A\)-궤도는 안장 곡면을 지나는 궤도의 형태를 띠고 있다.대략적으로 말하자면, 이런 성질들을 균등한 쌍곡성질이라 표현하며, 여기서 “균등한”이란 모든 \(x\in T^2\)에 대하여 \(f_A\)에 의한 \(v_-\) 방향의 축약과 \(f_A^{-1}\)에 의한 \(v_+\) 방향의 축약 계수가 1보다 작은 상수 \(\lambda \in (0,1)\)라는 상계^{upper bound}를 갖는다는 뜻이다.

Arnold’s cat map의 몇 가지 다른 성질을 살펴보자.이 중에는 몇 가지는 모든 균등한 쌍곡성질을 가지는 역학계에 공통으로 찾아볼 수 있다. 먼저 모든 점 \(x \in T^2\subset\mathbb{R}^2\)에 대해 그 점을 통하며 \(v_+\)와 평행한 선을 \(\tilde{W}^s(x) \subset\mathbb{R}^2\), 그리고 이 선을 \(T^2\)에 사영한 상을 \(W^s(x) \subset T^2\)라 표기하겠다. 고유벡터 \(v_-\)의 기울기가 무리수이기 때문에 \(W^s(x)\)는 \(T^2\)내에 조밀한 부분집합을 이루며, 모든 \(y\in W^s(x)\)에 대해서 \(n\)이 무한대로 갈때 \(W^s(f_A^nx)\)를 따라서 계산된 거리 \(d_{W^s(f_A^nx)}(f_A^nx,f_A^ny)\)는 비율 \(\lambda_-\)로 기하급수적으로 축약한다. 때문에 \(W^s(x) \subset T^2\)는 안정적인 다양체^{stable manifold}라 불린다. 반대로 \(v_+\)를 사용해 정의되는 \(W^u(x)\)는 \(f_A\)에 의해 기하급수적으로 확대되며 불안정적인 다양체^{unstable manifold}라 불린다. 이러한 \(W^{s/u}(x)\)의 축약과 확대되는 성질은 \(f^n_A\), \(n \leq 0\),에 의해 역으로 전환되며, 이 두 가지 성질을 일컬어서”쌍곡성질”이라 부른다.

Arnold’s cat map의 또 다른 주목할 만한 성질은 재귀성^recurrence과 수많은 주기점^{periodic orbit}의 존재이다. 우리는 어렵지 않게 모든 유리수 \(x:=p/q \in T^2\)가 \(f_A\)의 주기점인걸 확인할 수 있다 (ie, \(f_A^nx = x\)를 만족하는 자연수 \(n\in N\)이 존재한다). 특히 모든 주기점의 집합은 \(T^2\)내에 조밀한 집합을 이룬다. 또 다른 \(f_A\)의 흥미로운 성질은 궤도 \(\{f_A^ny\}_{n\in Z}\)가 조밀한 집합을 이루는 점 \(y\in T^2\)의 존재이다. 달리 말해 임의의 열린 부분집합 \(U \subset T^2\)가 주어졌을 때, 얼마나 \(U\)의 크기가 작든지 간에 충분한 시간이 흐르면 \(y\)의 궤도가 \(U\)를 방문한다는 뜻이다. 이 성질을 추이적임^transitivity이라 부른다.

또한 \(f_A\)는 시작점에 예민한 성질^{sensitivity to initial condition}을 가진다. 이 성질은 시작점의 아주 조그만 변화가 (\(x\)에서 \(x’\)로) 그들의 장기적 궤도 (\(f^n_Ax\)와 \(f^n_Ax’\), \(|n|\gg 0\))에 큰 변화를 가져온다는 뜻이며, 확장성^expansivity이라는 성질과도 연관이 있다.

이러한 성질들을 처음 접하게 되면 크게 놀랍게 느껴지지 않을 수도 있지만, 임의의 역학계에서 이러한 성질들을 모두 찾아보기는 쉽지 않다. 쉬운 예시로는 원 위의 회전 \(R_a\)을 포함한 등거리 변환⁴ \(f\)에서는 두 점의 거리가 반복된 \(f\)에 의해 변하지 않으며, 그 때문에 원의 어떤 부분집합도 \(R_a\)에 의해 축약 또는 확대하지 않는다. 또한 \(a\) 가 유리수인 경우, 모든 점 \(x\in \mathbb{S}^1\)은 같은 주기의 주기점이다. 반대로 \(a\)가 무리수인 경우, 무리각 회전 \(R_a\)는 주기점이 하나도 없지만 모든 점 \(x\in \mathbb{S}^1\)의 궤도 \(\{R^n_a x\}_{n\in Z}\)는 \(\mathbb{S}^1\)내에 조밀한 집합을 이룬다.

조금 다른 예시로 3차원 원환면 \(T^3:=T^2 \times \mathbb{S}^1\)에 작용하는 직접곱 역학계 \(F_{A,id}:=f_A \times id \colon T^2 \times \mathbb{S}^1 \to T^2 \times \mathbb{S}^1\)을 고려해보면, 모든 점 \(z = (x,y)\in T^3\)의 \(F_{A,id}\)-궤도는 얇은 조각 \(T^2 \times \{y\} \in T^3\)을 벗어나지 않으며, 때문에 \(T^3\)내에 \(F_{A,id}\)-궤도가 조밀한 점 \(z\in T^3\)는 존재하지 않는다. 반대로 모든 얇은 조각 \(T^2 \times \{y\}\)위에 수많은 주기점이 존재한다.

또 다른 예시로는 무리수 \(a \not\in \mathbb{Q}\)를 사용해 정의된 직접곱 역학계 \(F_{A,a}:=f_A \times R_a \colon T^2 \times \mathbb{S}^1 \to T^2 \times \mathbb{S}^1\)는 (무리각 회전 때문에) 주기점이 하나도 없다. 또한, 두 번째 좌표축 \(\mathbb{S}^1\) 상의 거리 \(|y_1-y_2|\)가 짧은 \(T^3\)의 두 점 \(z_1=(x,y_1)\)와 \(z_2=(x,y_2)\)의 \(F_{A,a}\)-궤도상의 거리 \(d(F_{A,a}^nz_1,F_{A,a}^nz_2)\)는 \(n\in Z\)에 관계없이 보존된다. 이러한 이유는 두번째 좌표축 \(\mathbb{S}^1\)은 \(F_{A,a}\)에 의해 확대 또는 축약하지 않기 때문이다. 첫번째 (2차원) 좌표축 \(T^2\)는 \(f_A\)에 의해 쌍곡성질을 보이는걸 고려하면, \(F_{A,a}\)는 쌍곡성질과 그에 반대되는 성질이 공존한다고 볼 수 있다. 이러한 역학계는 부분적 쌍곡성질^{partial hyperbolicity}을 가진다 일컬으며, 도입부에서 언급된 스펙트럼에는 중간쯤에 위치한다 볼 수 있다.

(2) 아노소프의 미분동형사상^{Anosov diffeomorphism}

이번 세부 챕터에서는 균등한 쌍곡성질에 대해 살펴볼 것이다.콤팩트 리만 다양체 \(M\)와 미분동형사상 \(f \colon M \to M\)가 주어졌을 때, 모든 점 \(x\in M\)의 근방에 \(f^n\)에 의한 기하급수적 축약과 확대하는 성질이 공존하면 \(f\)를 수학자 Dmitri Anosov의 이름을 따 Anosov 미분동형사상^{Anosov diffeomorphism} 혹은 균등한 쌍곡성질^{uniform hyperbolicity}을 가지는 역학계라고 부른다.⁵ 조금 더 설명하자면, 주어진 Anosov 미분동형사상 \(f\colon M\to M\)에 대해 모든 점 \(x\in M\)의 국소 근방은 \(f\)에 의해 보존되는 두 개의 서로 횡단^transverse하는 엽층구조^foliation를 가지고 있다. 두 개의 엽층구조는 각각 안정된 부분 다양체^{stable manifold}라 불리며 \(W^s\)로 표기되고 불안정된 부분 다양체^{unstable manifold}라 불리며 \(W^u\)로 표기된다.⁶ Arnold’s cat map과 비슷하게 \(f^n\)에 의해 (\(n\geq 0\)) 안정된 부분 다양체는 기하급수적으로 축약하며, 불안정한 부분 다양체는 기하급수적으로 확대한다. 이게 정확한 Anosov 미분동형사상의 정의는 아니지만, 결국엔 \(f\)의 축약과 확대하는 성질이 핵심이다.⁷

지금부터 Anosov 미분동형사상의 몇 가지 성질을 살펴보도록 하겠다. 이 중에는 위에서 살펴본 Arnold’s cat map의 성질과 상당수 겹치는 부분이 있다. 첫번째 주목할 만한 성질은 위에서도 언급되었고 카오스와 연관되는 시작점에 예민한 성질이다. 또한 축약과 확대하는 성질을 이용해서 어떤 점 \(x\in M\)가 시간이 흘러 다시 시작점 \(x\) 근처로 돌아오면 그 궤도를 비슷하게 따라가는 주기점을 찾을 수 있다.⁸ 이러한 성질에 의해, 수많은 주기점을 찾을 수 있으며 이런 주기점들은 Anosov 미분동형사상을 연구하는데 큰 역할을 한다. 하나의 예시를 들자면, 모든 주기점들에 한해서 어떠한 성질이 성립된다면 이 같은 성질이 리만 다항체 \(M\) 전부에서 성립하는 경우가 종종 있다. 전자가 후자보다 훨신 쉽다는걸 감안하면, 이런 류의 결과는 아주 유용하며, 잘 알려진 리브식\(^{\text{Liv}\check{s}\text{ic}}\) 정리가 여기에 속한다[2].

주기점에 관해 짚고 넘어가야 할 또 다른 부분은, 모든 Anosov 미분동형사상에 수많은 주기점들이 존재하지만, 주기점들의 집합이 조밀한 부분집합을 이루는지는 밝혀지지 않았다.이 의문은 오래된 추측으로써, Anosov 미분동형사상의 여러 가지 다른 오래된 추측과 동일한 내용을 내포하고 있다. 예를 들면 주기점들의 조밀함에 관련된 추측을 증명하면, Anosov 미분동형사상이 정의될 수 있는 리만 다양체에 관련된 추측과 그리고 추이적임을 주장하는 추측도 동시에 해결하게 되는 것이다.

마지막으로 살펴볼 Anosov 미분동형사상의 성질은 구조적 안정성이다. 이 성질을 설명하기 위해서는 먼저 위상학적 켤레변형^{topological conjugacy}이란 개념을 이해해야 한다. 두 개의 위상학적 역학계 \((X,f)\)와 \((Y,g)\)에 대해

\(h \circ f = g\circ h\)

를 만족하는 위상동형 \(h \colon X\to Y\) 존재할 때, \(f\)와 \(g\)를 서로의 위상학적 켤레라 부른다. 위 수식을 말로 풀어보면, 왜 “켤레”라 불리는지 쉽게 알 수 있다: 먼저 \(h\)를 이용해 \(X\)에서 \(Y\)로 변형 후 \(g:Y \to Y\)로 변형하는 것과, 먼저 \(f:X \to X\)로 변형 후 \(h\)로 변형하는 결과가 같다는 뜻이다. 즉, \(h\)를 두 역학계 \(f\)와 \(g\)를 이어주는 연결고리라 볼 수 있고, 위상학적 관점에서 보았을 때 \(f\)와 \(g\)는 본질적으로 같은 역학계이다.

주어진 미분동형사상 \(f \colon M \to M\)이 임의의 작은 섭동에 의해서 다른 미분동형사상 \(g\colon M \to M\)으로 변형되었을 때, 두 미분동형사상 \(g\)와 \(f\)가 서로의 위상학적 켤레이면 \(f\)가 구조적 안정성^{structural stability}을 가지고 있다고 표현한다. 구조적 안정성은 역학계의 위상학적 구조가 작은 섭동에 의해 변하지 않는 성질을 의미하며, 모든 Anosov 미분동형사상은 이러한 성질을 가진다. 글 도입부에서 언급된 구조가 보존되는 성질이 여기에 해당한다.

구조적 안정성은 아주 특별한 성질이며, 이러한 성질을 가지지 않은, 즉 작은 섭동에 의해 위상학적 구조가 완전히 바뀌는, 동역계도 쉽게 찾아볼 수 있다. 간단한 예시로는, 원 위의 무리각 회전은 아주 작은 섭동으로 유리각 회전으로 변형될 수 있으며, 위에서 주기점에 관해 설명하며 살펴보았듯이 두 역학계는 확연히 다른 위상학적 성질을 가지고 있다.

3. 위상학적 엔트로피^{Topological Entropy}

이번 챕터에서는 역학계의 복잡도를 나타내는 개념 중 하나인 위상학적 엔트로피를 설명하려고 한다. 거리함수 \(d\)가 정의된 콤팩트 위상공간 \(X\)와 연속변환 \(f\colon X \to X\)이 주어졌을 때, 자연수 \(n\in \mathbb{N}\)에 대해서 “구별 가능한” 길이 \(n\) 궤도^{length n orbit}의 개수를 \(E_n\)이라 부르자. 역학계 \(f\)가 복잡한 구조를 가지고 있다면, \(n\)이 늘어날수록 구별 가능한 길이 \(n\) 궤도의 개수 \(E_n\)도 늘어날 것이며, 위상학적 엔트로피란 \(E_n\)의 기하급수적 성장률을 나타낸다. 직관적으로도, \(f\)가 더 복잡할수록 \(E_n\)도 더 빠르게 늘어날 것이며, 따라서 더 큰 위상학적 엔트로피를 가질 것이다. 엔트로피에 대한 대략적인 개념을 이해했다면 이제 조금 더 구체적인 정의를 살펴보자.

위 문단에서 주목해야 할 부분은 “구별 가능한 궤도”를 어떻게 정의하냐 인데, 직관적으로 생각해 보았을 때 임의의 두 점 \(x,y \in X\)이 모든 \(0 \leq k \leq n-1\)에 대하여 거리 \(d(f^kx,f^ky)\)가 작다면, 두 점의 길이 \(n\) 궤도 \(\{f^kx\}_{k=0}^{n-1}\)와 \(\{f^ky\}_{k=0}^{n-1}\)가 서로 가깝다고 볼 수 있다. 이러한 관점으로 볼때, 구별 가능한 궤도란 서로 너무 가깝지 않은 두 궤도를 의미한다. 특히 임의의 상수 \(\varepsilon >0\)가 주어졌을 때 모든 \(0 \leq k \leq n-1\)에 대해 거리 \(d(f^kx,f^ky)\)가 \(\varepsilon\)보다 작다면, 두 점의 길이 \(n\) 궤도는 \(\varepsilon\)-스케일로 구별 가능하다고 볼 수 있다.

길이 \(n\) 궤도가 \(\varepsilon\)-스케일로 구별 가능한 점들의 최대 집합을 구했을 때, 이 집합의 크기를 \(E_{n,\varepsilon}\)이라 하고 \(\varepsilon\)-스케일 엔트로피^{entropy at scale \(\varepsilon\)}를 \(E_{n,\varepsilon}\)의 기하급수적 성장률로 정의하고 \(h_\varepsilon(f)\)로 표기한다. 여기서 주목할 점은 \(\varepsilon\)가 줄어들면, \(\varepsilon\)-스케일 엔트로피 또한 단조증가하며, \(\varepsilon\)이 0으로 수렴할 때 \(\varepsilon\)-스케일 엔트로피는 위상학적 엔트로피^{topological entropy}라⁹ 불리우는 수로 수렴한다:

\(h_{top}(f) := \lim\limits_{\varepsilon \to 0} h_\varepsilon(f).\)

즉, 위상학적 엔트로피 \(h_{top}(f)\)는 아주 작은 스케일로 보았을 때 구별 가능한 서로 다른 \(f\)-궤도의 개수의 기하급수적 성장률이라 볼 수 있다. 특히, 주어진 역학계가 양의 엔트로피를 가진다면, 궤도의 개수의 기하급수적 성장률을 카오스 연관 지어 볼 수 있다.¹⁰

위상학적 엔트로피의 가장 중요한 성질 중 하나는 위상학적 켤레변형에 의해 보존된다는 사실이다. 이 성질은 여러 가지 역학계들이 서로 위상학적 켤레가 아니라는 것을 보이는데 사용되고, 때문에 역학계들을 분류하는 연구 분야^{classification problem}에 큰 진보를 가져 왔다. 특히, 주어진 특정 쌍의 역학계들이 서로 위상학적 켤레가 아닐 거라는 추측이¹¹ 위상학적 엔트로피를 사용해서 쉽게 증명되었다. 여기서 주의할 점은 역은 성립하지 않는다는 사실이다. 특히 서로 위상학적 켤레가 아니지만 0의 엔트로피를 가지는 역학계들을 쉽게 찾아볼 수 있다.

이 성질에서 쉽게 유추할 수 있는 따름정리 중 하나는 위상학적 엔트로피 \(h_{top}\)는 구조적 안정성을 가지는 역학계 \((X,f)\)의 주변에 국소 상수 함수의 성질을 나타낸다는 것이다. 즉, Anosov 미분동형사상의 위상학적 엔트로피는 작은 섭동에 의해 변하지 않는다는 뜻이다.

위상학적 엔트로피는 일반적으로 계산하기가 어렵지만, 구체적인 계산이 가능한 몇 가지 예시가 존재한다. 첫번째로는 원 위의 회전 \(R_a\colon \mathbb{S}^1 \to \mathbb{S}^1\)은 0의 엔트로피가 가지고 있다. 일반적으로 더 나아가서, 콤팩트 리만 다양체에 정의된 모든 등거리변환 역시 0의 엔트로피를 가진다.

다른 예시로는 원 \(\mathbb{S}^1 = \mathbb{R} /\mathbb{Z}\)위에 \(x \mapsto 2x\)로 정의된 역학계의 구별 가능한 길이 \(n\) 궤도의 개수는 \(n\)이 1씩 늘어날 때마다 대략 두 배씩 늘어난다. 따라서 이 역학계 엔트로피는 \(\ln 2\)이며, 이 역학계의 두 배씩 확대하는 성질이 양의 엔트로피로 표현되었다고 볼 수 있다.

또 다른 예시로는, 모든 Anosov 미분동형사상 \(f\colon M \to M\)은 항상 양의 엔트로피를 가진다. Anosov 미분동형사상의 확장성 덕분에, \(\varepsilon\)이 적당한 한계점 \(\varepsilon_0\)보다 작을때 모든 \(\varepsilon\)-스케일 엔트로피 \(h_{\varepsilon}(f)\)는 같은 값을 가진다. 따라서, 위상학적 엔트로피 \(h_{top}(f)\)를 계산하기 위해서는 충분히 작은 \(\varepsilon\)을 고른 후 \(\varepsilon\)-스케일 엔트로피를 구하면 된다.

4. 위상학적 엔트로피의 성질과 쓰임

이 마지막 챕터에서는 위상학적 엔트로피와 관련된 다른 종류의 엔트로피에 대해 알아보려 한다. 그 전에 보존측도에 대해 조금 알아볼 필요가 있다. 주어진 역학계 \(f \colon X\to X\)와 측도 \(\mu\)가 모든 가측부분집합 \(A \subseteq X\)에 대해 방정식 \(\mu(f^{-1}A) = \mu(A)\)을 만족할 때, \(\mu\)를 보존측도^{invariant measure}라고 부른다.모든 보존측도의 집합을 \(M(f)\)라 표기하며, \(X\)가 콤팩트 위상공간일때 보존측도의 집합 \(M(f)\) 또한 콤팩트 공간이 된다.¹²

보존측도 \(\mu\in M(f)\)가 주어졌을 때, 이 측도에 관점에서 “보여지는” 측도에 관한 엔트로피^{measure-theoretic entropy} \(h_{\mu}(f)\)라는 개념이 존재한다. 이 개념의 정의는 고계원 교수님의 섞임에 관한 글 에서 이미 한번 소개되었기 때문에 이 글에서는 생략하도록 하겠다. 측도에 관한 엔트로피는 위상학적 엔트로피와 연관은 있지만, 두 개념은 서로 다른 개념이다. 예를 들면, 역학계가 양의 위상학적 엔트로피 \(h_{top}(f)\)를 가지고 있어도 주어진 보존측도 \(\mu\)가 단순하다면 (예를 들면 하나의 주기 궤도에 지지되어 있는 경우) \(h_{\mu}(f)\)는 0의 값을 가지게 된다.

\begin{equation}\label{eq: var prin}
h_{top}(f) = \sup\limits_{\mu\in M(f)} h_{\mu}(f).                          
\tag{4.1}\end{equation}                                                                                                                                                                              

변분 원리에서 엔트로피에 관한 두가지 사실을 유추할 수 있다. 첫번재는 측도에 관한 엔트로피는 항상 위상학적 엔트로피 보다 같거나 작다는 사실다. 두번째로는, 측도에 관한 엔트로피를 이용해 위상학적 엔트로피의 근사값을 구할 수 있다.

만약에 변분원리에서 상한값^supremum, 즉 위상학적 엔트로피 값을, 달성하는 보존측도 \(\mu \in M(f)\)가 존재하면, 그 측도를 최대 엔트로피 측도^{measure of maximal entropy}, 혹은 줄여서 mme라고 부른다. 모든 역학계가 mme를 가지는 것은 아니며, mme가 하나도 없는 여러 가지 구체적인 역학계가 존재한다. 이러한 이유는 엔트로피함수 \(\mu \mapsto h_{\mu}(f)\)가 상반연속^{upper semi-continous}함수가 아닐 때도 있기 때문이다.

존재한다는 가정하에 mme는 중요한 역할을 한다. 예를 들면, Anosov 미분동형사상을 포함 몇몇 역학계는 mme를 통해 주기점의 분포와 성장률에 관한 정보를 알수 있다. 또한 mme는 베르누이 성질^{Bernoullicity}, 중심극한정리, 대편차 원리, 섞임 등등 여러 가지 에르고딕 성질과 통계적 성질을 가지고 있는 경우가 자주 있다.

이러한 mme의 중요성을 살펴보았을 때, 자연스럽게 드는 몇 가지 의문이 있다: “어떤 역학계가 적어도 하나 이상의 mme를 보유할까? mme가 존재하는 역학계면, 몇개의 mme가 존재하며, 그들의 성질은 어떤 것들이 있나?”일반적인 경우에 임의의 주어진 역학계에 대해선 이런 질문의 답을 모르는 경우가 많다. 하지만 위에서 살펴본 몇 가지 예시 역학계 중에서는 답이 잘 알려진 경우가 있다.

먼저 무리각 회전 \(R_a \colon \mathbb{S}^1 \to \mathbb{S}^1\)은 르베그 측도^{Lesbesgue measure}라는 유일한 보존측도를 가지고, 때문에 이 측도는 자동으로 mme가 된다. 하지만 이 예시는 어차피 위상학적 엔트로피가 0이기 때문에, 다른 보존측도가 존재했어도 모두 mme로 분류 되었을 것이며, 특별히 흥미로운 예시는 아니다.

반면에 Anosov 미분동형사상은 수많은 보존측도가 존재한다.Anosov 미분동형사상의 확장성은 엔트로피함수 \(\mu \mapsto h_{\mu}(f)\)의 상반연속성을 보장하기 때문에, 적어도 하나의 mme의 존재는 쉽게 추론할 수 있다. 자세히 언급하지는 않겠지만 1974년에 Rufus Bowen[3] 이 specification이라는 성질을 사용하여 mme의 유일성을 증명하였다. 거의 50년이 지난 지금도 Bowen의 증명 방법은 여러가지 다른 역학계에도 응용되고 있다.

위에서 살펴본 두 개의 예시 모두 유일한 mme를 가지고 있지만, 두 예시 모두 특별한 이유에 의해 그러한 성질을 가지는 것이다. 아직도 mme의 존재 여부 조차 모르는 여러 역학계들이 존재하며, 이 글에서 살펴본 Anosov 미분동형사상 외 수많은 흥미로운 역학계에 관한 다양한 연구가 지금도 이루어지고 있다. 수학의 다른 분야보다 역사는 짧지만, 동역학계는 지난 수십 년간 기하학, 정수론, 해석학, 확률론 등등 여러 다른 수학의 세부 분야과 상호 작용하며 꾸준한 발전을 이뤄오고 있다. 또한 다양한 연구 문제들에 새로운 관점을 제시하며 이제는 서로 떼려야 뗄 수 없는 중요한 한 분야로 자리 잡았다. 이 글을 시작으로 동역학계의 여러 가지 이론과 발견을 더 접할 기회를 가지길 권장한다.