시각의 과학 – 상 맺기

우리는 “색각의 과학“이라는 글에서 생명체가 왜 또는 어떻게 특정 색깔의 빛을 볼 수 있게 되었고, 어떠한 방식으로 색을 인지하며, 왜 동물들마다 색을 인지하는 방식이 같지 않으며, 왜 그렇게 진화되었는지 이야기를 나누었다. 무한히 펼쳐져 있는 전자기파의 전체 스펙트럼에서 생명체가 볼 수 있는 가시광선 영역은 아주 좁은 부분으로 약 400 – 700 nm의 파장을 갖는 연속적인 전자기파 영역이다. 생명체에 따라 1가지에서 4-5가지의 서로 다른 중심파장을 감지하는 광수용체가 있어 이들을 자극하는 정도(상대적 비율)를 비교함으로써, 그 비율을 색으로 해석해 낸다.

서양 미술사에서 아주 유명한 사조로 점묘파^Pointillism가 있다. 너무 느리고 힘든 작법에 바탕을 둔 화풍이라서 실제 이에 동참한 예술가는 다른 사조에 비해 많지는 않았다. 조르주 쇠라^{Georges Seurat}가 가장 유명하며 이 사조의 비조로 간주된다. 19 세기 후반에, 색 또는 (색)지각에 대한 과학 지식이 비약적으로 발전하고 있었는데, 점묘파는 미술이 과학적 사실을 수용한 의미 있는 큰 걸음이었다. 양탄자에서 인접한 서로 다른 색상의 실이 제 3의 색으로 나타나는 것, 두 색을 물감으로 섞을 때와 빛으로 섞을 때 결과가 다른 것 등 색과 빛에 대한 새로운 지식이 생겨나고, 세상 속으로 전파되고 있었다 [1]. 쇠라는 이에 착안하여, 물감이나 빛을 섞어서 다양한 색을 나타내는 대신, 공간적으로 분리되어 있지만 근접해 있어 우리 눈으로는 분간하기 힘든 서로 다른 색의 점으로 새로운 색을 창조하고자 하였다. 즉, 물감을 혼합하여 색을 만드는 대신, 인간의 망막에서 혼합이 일어나게 하려는 것이었다. 이는 놀라운 발상이었고, 이들의 독창적인 작품들은 미술관과 미술책에서 꼭 보게 되는 예술품이 되었다. 필자는 시카고 미술관^{The Art Institute of Chicago}에서 쇠라의 “그랑자트의 일요일 오후^{Un dimanche après-midi à l’Île de la Grande Jatte}”를 처음 본 순간의 강렬함을 아직도 기억하고 있다 [그림 1]. 원색의 점들을 찍어서 모든 색을 표현하는 작품이 매우 신기하였고, 사진을 통해 보거나 일정 거리 떨어져서 감상하는 것과 실물을 가까이에서 보는 것의 차이가 뚜렷하였다.

그러면 왜 근접한 곳에서 나오는 두 빛이 망막에서 섞일 수 있을까? 설사 무한히 작은 점에서 나온 빛이라도 렌즈로 맺은 상은 점이 아닌 일정한 크기를 갖기 때문이다. 두 근접한 점 (한 점은 빨강, 다른 점은 초록빛을 낸다고 하자.)에서 나온 빛은 망막에서도 근접한 곳에 도착하게 되는데, 상의 크기가 유한해서 둘이 겹치게 된다. 겹친 부분에 있는 망막은 빨강, 초록빛을 동시에 느끼게 되고 이는 노란 빛이 도착한 것과 같은 효과를 낼 것이다.

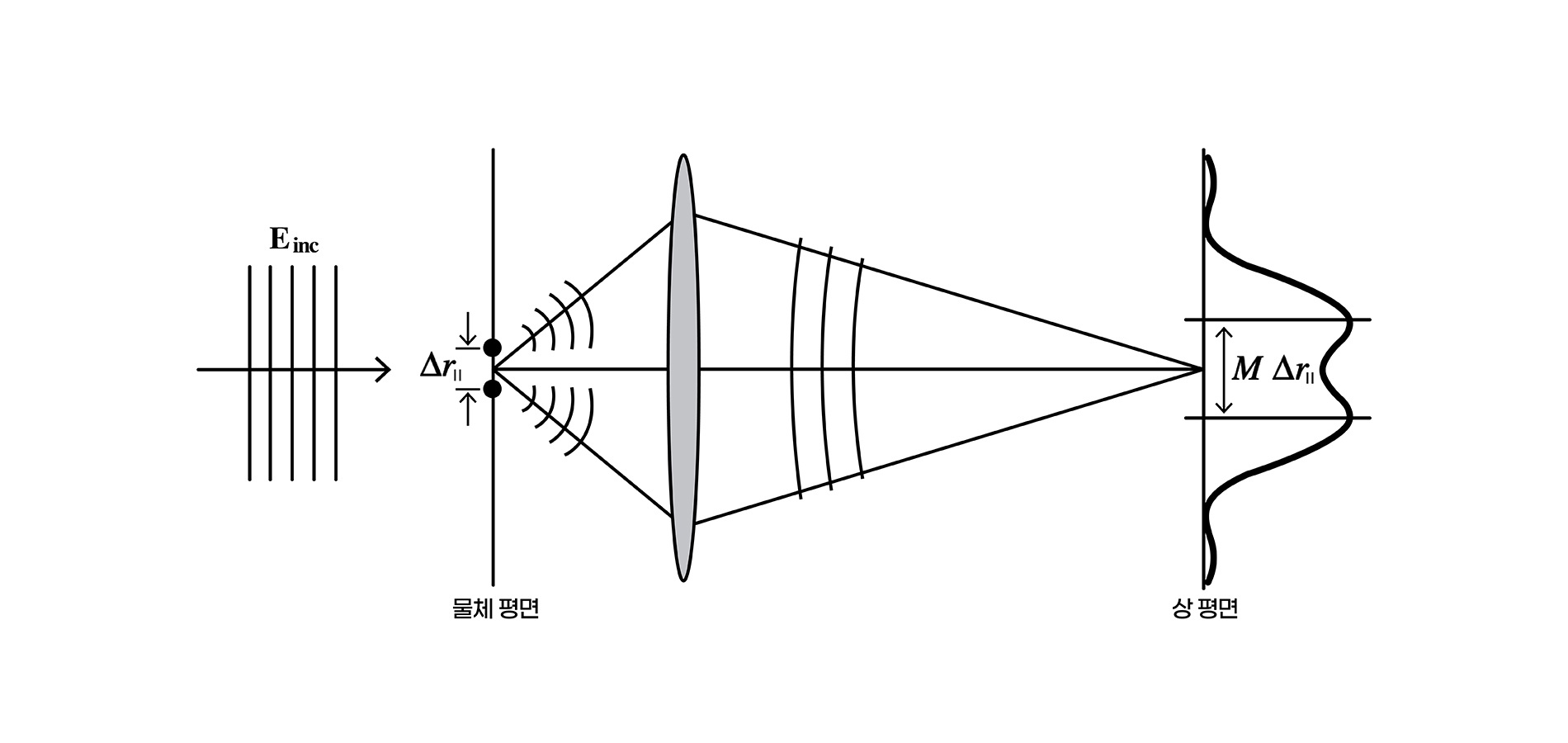
빛을 렌즈로 집속할 때, 상의 크기가 유한한 것은 파동의 기본 속성이다. 파장 \(\lambda\) 인 빛으로 만드는 상의 최소 크기에 대해 약 100여 년 전에 제시된 식 두 가지가 있다. 이 둘은 사실 거의 같다고 보면 되는데, 하나는 아베 에돌이 한계(Abbe diffraction limit; \(\Delta r_{\parallel} = \frac{\lambda}{2 n \sin \theta} = \frac{\lambda}{2 NA}\) , 1873)이고 다른 하나는, (각도 분해능에 대한) “레일리의 기준^{Rayleigh criterion}( \(\Delta \theta \sim 1.22 \frac{\lambda}{D}\) , 1879)”이다. 후자는 지름이 \({D}\)인 원형 구멍 (또는 렌즈)을 통해, 시야각이 적어도 \(\Delta \theta\)  만큼 떨어진 두 물체를 구별할 수 있다는 분해능의 기준을 제시하는 식이다. 아베 에돌이 한계에 등장하는 NA^{numerical aperture}(\(NA = n \sin \theta\))는 개구수라고 하며 빛을 얼마나 많이 모으는지에 관련된 값이다. 아베를 기념하는 조각물 [그림 2]에 새겨져 있는 에돌이 한계 식은 아베의 업적을 상징적으로 표현한다. 같은 평면에 놓인 두 물체가 상을 맺을 때, 물체의 구별 가능 여부를 [그림 3]을 통해 이해할 수 있다.

에돌이 한계는 유한한 파장을 갖는 파동으로 상을 맺는 경우에는 절대적으로 벗어날 수 없는 굴레와 같아 영상의 세밀함을 규정짓는 절대적인 기준으로 한 세기를 군림해왔다. 하지만 지난 세기 말부터 이번 세기 초에 일어난 일련의 새로운 시도는 에돌이 한계를 우회할 수 있는 놀라운 가능성을 제시하였다.

발광체(형광염료)가 레일리 기준보다 조밀하게 분포할 때, 영상을 찍으면 구별할 수 없는 많은 점들이 다닥다닥 붙어 밝게 빛나는 영상을 보게 될 것이다. 즉, 에돌이 한계로 퍼져 입사하는 입사광으로 염료들이 있는 공간을 한꺼번에 비추면 이들이 모두 들뜨게 되고 형광을 방출하게 된다. 렌즈로 구성된 영상 장치를 통해 상을 맺게 하면 이들이 모두 유한한 크기를 갖는 밝은 점들로 상을 맺으므로, 레일리 기준보다 가까이 있는 염료들에서 나오는 형광은 영상면에서 겹쳐 나타나 구별이 어렵게 된다. 편광, 파장, 방출 시간 등의 차이로 이들 발광체를 구별하는 것이 가능하면 겹치는 문제를 해결할 방법을 찾을 수 있지만, 구별할 수 없다면 새로운 전략이 필요하다. 그래서 착안한 방법이, 가까이 있는 형광분자들이더라도 동시에 형광을 내는 들뜬 단계에 두지 않는 것이다. ‘어떻게’가 중요한 질문일 것이다. 만약 소수의 형광 분자들만 빛을 내어 카메라에 상을 맺는다면 중심점을 찍어 나가는 방법 등을 통해 세밀한 영상을 얻을 수 있다 (아래 설명 참조).

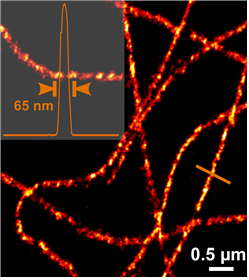
가장 먼저 제시된 방법이, STED^{stimulated emission depletion}라는 기술이다. 이는 괴팅겐의 슈테판 헬^{Stefan Hell} 교수가 제시한 방법으로 [그림 4]에서와 같이 입사광과 함께 입사광의 파장보다 약간 긴 파장을 갖는 도넛 형태의 빛을 함께 조사해주면 도넛 빛이 닿은 부분의 형광염료는 유도 발광^{stimulated emission}(아인슈타인이 이론적으로 발견하였고 후에 실험적으로 입증되었으며, 레이저 작동의 기본원리이다.)에 의해 미리 소광되어 형광을 낼 수 없게 된다. 따라서 처음 조사된 영역 중 도넛 빛의 세기가 미미한 중심부에 있는 형광염료만  빛을 낼 수 있게 되어, 실질적으로 형광을 낼 수 있는 분자가 크게 줄어들게 된다. 그렇게 되면 카메라에 적은 수의 구별 가능한 점만 한 번에 찍히게 된다. 조사광과 도넛 빛의 중심을 정확히 일치시킨 상태로 샘플면을 훑으면서 (raster scan)영상을 찍으면 2차원 영상을 얻을 수 있다. 이러한 전략을 통해, 그렇지 않은 경우에 비해 훨씬 선명한, 분해능을 넘어서는 영상을 얻게 된다 [그림 5].

얼마 지나지 않아, 새롭게 제시된 분해능 극복 방법은 다음과 같다. 형광염료 자체가 형광을 낼 수 있는 상태와 (빛을 맞아도) 형광을 낼 수 없는 상태를 가질 수 있다고 하자. 보통 이런 형광염료는 빛을 내고 내지 않는 상태를 반복하며 깜박거리는데, 형광염료 자체로 보면 나쁜 특성을 갖고 있다고 할 수 있다. (갑자기 아무 형광을 내지 않으면 형광 표지된 대상체의 위치를 알 수 없다. 다시 켜지면 원래 보던 것과 같은지 알 수 없다.) 이런 “쓸모없는” 염료에서 놀라운 가능성을 발견하게 된다. 방출 가능/불가능 상태를 적절한 방법으로 제어할 수 있다면, 다수의 형광염료가 있는 상태에서 일부만 가능 상태로 놓고 영상을 찍고, 이 분자들이 불가능 상태로 바뀌면 마침 다른 것들이 가능 상태가 되어 찍고, 이러한 일을 반복하면 분해능을 넘어서는 세밀한 영상을 얻을 수 있을 것이다. 이 방법이 PALM^{photo-activated localization microscopy} 또는 STORM^{stochastic optical reconstruction microscopy}이라고 불리는 초고분해능 형광 이미징 방법이다 [그림 6]. 이에 대한 업적으로 버클리 소재 캘리포니아 대학교에 재직 중인 에릭 베칙^{Eric Betzig} 교수와, 단분자의 흡광을 처음으로 발견하고 측정한 스탠퍼드 대학교의 윌리엄 모너^{W. E. Moerner} 교수, 앞서 소개한 슈테판 헬 교수가 2014년 노벨 화학상을 받았는데, 세 명의 물리학 박사가 생물학/이미징에 혁명적인 기여를 한 공로로 노벨 화학상을 받은 흥미로운 경우였다. 백여 년 간 군림해온 아베 에돌이 한계라는 ‘절대적인 한계’를 특별한 경우이기는 하나 극복해낸 업적이 인정받은 것이라고 할 수 있다.

PALM, STORM 방법에 대해서 약간 부연 설명이 필요하다. 앞서 언급한 바와 같이 한 점에서 나온 빛을 원형 구멍(렌즈)을 통과시켜 상을 만들면, [그림 7]처럼 가운데가 세고 가장자리로 갈수록 약해지는 모양이 될 것이다. 이런 행태라는 것을 안다면 이 정보를 요긴하게 이용할 수 있다. 이 모양은 영국의 천문학자 George Biddell Airy 이름을 따서 Airy 함수 형태라고 부른다. (이는 1종 베셀함수 중 1차 베셀함수의 형태(\( J_1(x)\))와 관련이 있다. 하지만 더 친숙한 가우스 함수로 근사해도 별로 차이가 나지 않는다.) 이러한 퍼진 점 형태의 영상을 얻으면, 우리는 바로 그 중심이 발광자의 위치임을 알 수 있다. 이러한 점들의 중심을 찾아서 그 점을 모으면 매우 세밀한 영상을 얻을 수 있다.

시각의 주제로 다시 돌아오자. 아주 가깝게 놓인 점을 우리 눈으로만 구별하는 것은 매우 어려울 수 있다. 1 mm²에 평균 20만 개(최대 32만 개) [2]의 시세포가 있다고 하므로 시세포 사이의 거리는 대략 2.5 \(\mu\)m가 된다. 같은 시세포에 떨어진 신호는 구별 불가능하다고 가정할 때, 두 점에서 오는 빛을 구별하려면, 적어도 망막에 2.5 \(\mu\)m 떨어져 들어와야 한다. 안구의 크기를 대략 25 mm라고 하면, 2.5 \(\mu\)m는 분리각으로 ~ 10^–4 rad이 된다. 이는 약 0.3 arcmin이 되며, 이 차이를 구별하는 것(10 m 떨어진 곳에 있는 1 mm 간격의 두 점을 구별)이 최대 시력이 된다 (\(1 {~\rm arcmin} \sim \frac{1}{60} \times \frac{\pi}{180} \sim 291~ \mu {\rm rad}\); 1 arcmin을 구별하는 것을 시력 1.0으로 정의하며, 5 m 떨어진 곳에서 1.5 mm의 간격을 보는 것에 해당함). 더 가깝게 붙어 있는 점들은 구별할 수 없으며, 돋보기, 현미경 등을 이용해서 간격을 크게 한 후 볼 수밖에 없을 것이다. 동공의 크기를 ~1.5 mm로 가정하고, \(\lambda\)= 600 nm에 대해 레일리 기준을 고려하면 \(\Delta \theta \sim 1.22 \frac{\lambda}{D} \sim ~600 ~\mu {\rm rad} \sim 2 {~\rm arcmin}\)이 되어 대략 \(\left( \frac{15 ~\mu {\rm m}}{2.5 ~\mu {\rm m}} \right)^2 \sim 36\) 개의 시세포에 퍼지게 된다. 만약 점묘파 그림에서 이웃한 두 점이 \({s}\) mm 떨어져 있고, \({d}\) m 만큼 떨어져서 그림을 보면 그 두 점의 분리각은 \(\frac{s}{d} \times 10^{-3}\) 이 된다. \({s}\) ~ 2일 때, \({d}\) > 3.3 을 만족하면 두 점에 의한 상은 레일리 기준보다 가까워서 구별이 되지 않고 두 점이 겹쳐지는데 이로써 두 점의 색이 망막에서 혼합되게 된다.

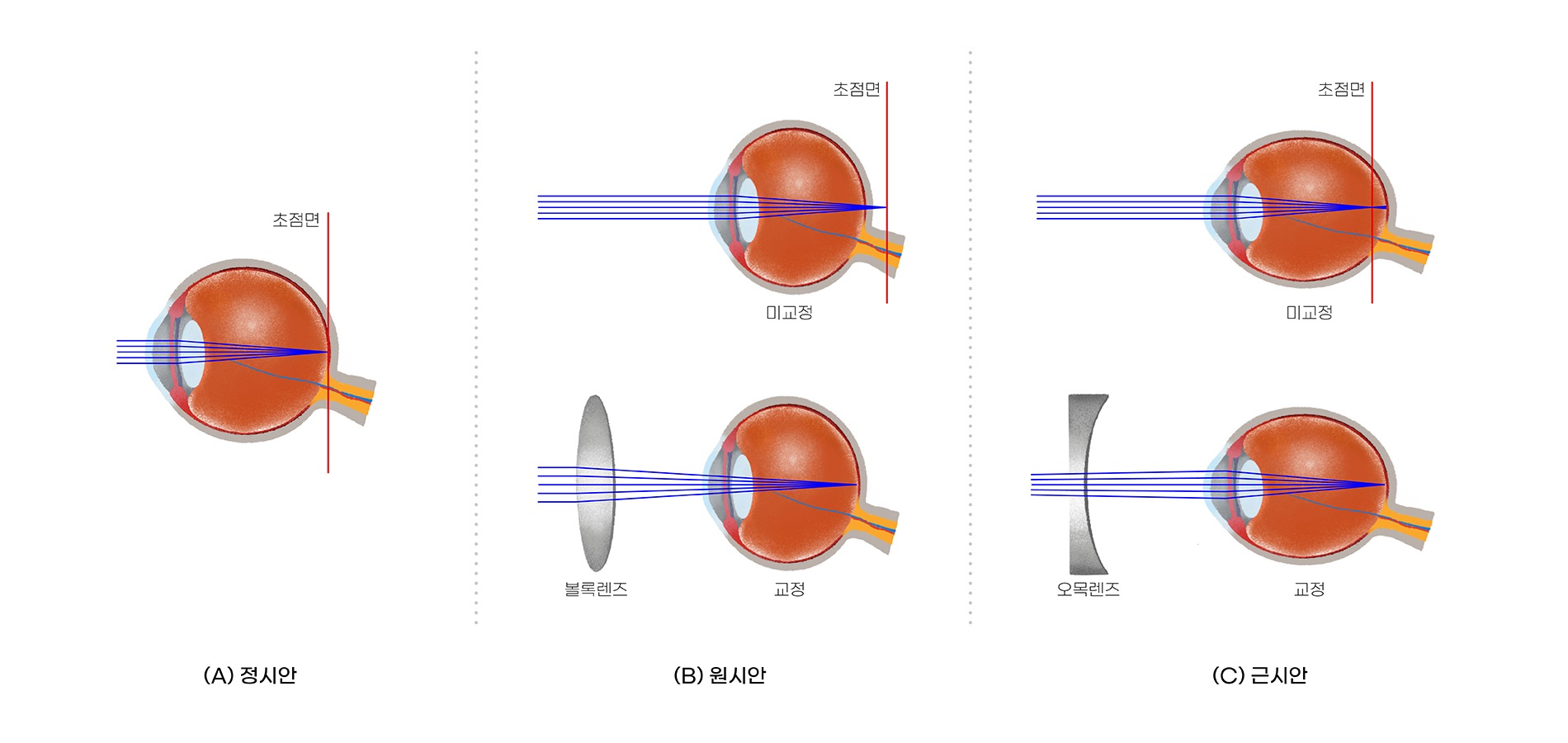
많은 사람들에게 시야가 흐릿한 것은 에돌이 한계 때문이 아니다. 우리 눈의 구조를 먼저 생각해보자 [그림 8]. 우리 눈, 안구는 구형을 띄고 있다. 두 개의 안구가 두개골에 박혀 있다. 두 눈으로 세상을 보는 것이 거리감 또는 입체감을 느끼는 데 중요한 요소가 된다. 안구의 앞쪽에 빛이 들어가는 동공이 있고, 조리개처럼 광량을 조절해주는 홍채가 있다. 동공의 앞에 볼록렌즈 형태를 갖는 각막이 있고, 굴절도 조절용 렌즈인 수정체가 있다. 빛이 들어오는 각막이 혼탁해져 시력이 나빠지는 병이 백내장이다. 유리액으로 차있는 안구 내부를 지나면 반대편 끝에 시각에 핵심적인 망막이 있으며 여기에서 감지된 신호는 시신경을 타고 뇌로 전달된다. 수정체의 조절로 망막에 정확한 상을 맺음으로써 우리는 외부 물체의 모양을 선명히 감지하고 이해하게 된다. 따라서 수정체와 망막이 시각에 가장 중요한 요소로 볼 수 있다. [그림 3]에서 이들은 각각 렌즈, 스크린에 해당한다. 수정체의 변형으로 웬만큼 가깝거나 먼 물체의 상을 망막에 선명하게 만들 수 있지만 그렇지 못한 경우가 사실 더 흔하다 [그림 9]. 수정체가 가까운 물체를 보는 데 적합하게 되어 먼 곳에 있는 물체의 상을 망막 앞에 맺는 것이 근시^{near-sightedness, myopia}이다. 이를 보정하기 위해 빛을 더 퍼트려서 안구에 넣어주기 위해 오목렌즈를 쓰게 된다. 반대로 모양체근의 기능이 약화되어 수정체를 충분히 응축시키지 못해 가까운 물체를 보기에 충분할 만큼의 굴절을 일으키지 못하면 원시^{far-sightedness, hyperopia}가 된다. 이를 보정하기 위해 빛을 더 모아줄 수 있는 볼록렌즈, 즉 돋보기를 쓰게 된다. 나이가 40대 중후반에 이를 때 보통 나타나는 노화 현상이라 이를 노안이라고 부르기도 한다.

근시가 왜 예전에 비해 훨씬 흔해졌는지에 대해 수십 년에 걸친 논쟁이 있어 왔다. 약 30 년 전에 미국에 25% 정도였던 근시 인구는 지금 42%가 되었고 2050년이면 절반을 넘을 것으로 예상된다 [3]. 특히, 80 년 전에 10% 정도 불과했던 중국의 근시 인구는 이제 90%가 넘는 10대들이 근시이다 [4]. 우리나라를 포함한 아시아 국가의 청소년은 80-90%가 근시라는 것 [4]은 긴 세월에 걸쳐 변화하는 유전자 변화에 의한 효과로 설명되기에 너무 크다. 따라서 시청각 매체에 많이 노출되었는지 여부, 독서 활동처럼 가까이 보는 활동을 많이 했는지 여부 등이 환경적 원인으로 제기된 바 있다. 대규모, 장기간 연구를 통해 다양한 가설 및 가능성을 배제하고, 가장 타당하고 상관성 높은 인자로 밝혀진 것이, 얼마나 강한 빛에 노출되었는지 여부이다 [3,4]. 즉, 강한 빛에 많이 노출되면 근시의 가능성이 낮고 반대로 강한 빛에 노출되지 못했다면 근시의 가능성이 높아진다는 것이다.

이 얘기를 듣고, 대학 때 의학에 관한 교양 수업에서 안과 교실 교수님으로부터 ‘안경을 쓰면 안구가 커진다’는 속설이 있지만 사실은 본말이 전도된 것이라는 얘기를 들었던 기억이 났다. 즉, ‘성장기 때 안구가 커져서 (근시자용) 안경을 쓰게 된다’는 것이다.

빛에 노출되는 것과 안구의 크기가 흥미롭게 연결된다. 강한 빛에 노출되면, 도파민이 분비되며 안구의 성장을 둔화시키지만, 실내 활동은 빛 자극을 억제하여 안구가 과도하게 커지게 함으로써 망막이 수정체에서 더 멀어지므로 상이 앞에 맺히게 되어 자연스럽게 근시로 전이된다는 것이다. 사례 연구들로부터도 이러한 상관성이 밝혀졌고 [5,6], 병아리를 이용한 생물학적 연구로부터도 타당성이 입증되었다 [3,4,7].

필자는 초등학생 때 맑은 날에는 밖에서 한낮 1 – 2 시간씩 외부활동을 해서인지, 대학을 다 마치고 대학원에 진학한 지 2년이 다 되도록 안경을 쓸 필요가 없는 좋은 시력을 유지했는데, 대학원에서 광학을 전공하여 극히 어두운 암실에서 연구를 하다 보니 단 몇 개월 만에 예전에 잘 보던 칠판 글씨를 맨눈으로는 선명하게 볼 수 없게 되었다. 성인에게 미치는 빛의 (부재의) 효과가 성장기 어린이에 비해 약하다고는 하나, 이러한 개인적 경험이 근시의 원인과 매우 잘 부합된다.

사람들이 뭔가를 정확히 보고 싶으면 흔히 하는 행동이 눈을 가늘게 뜨고 보는 것이다. 이를 영어로 squinting이라고 하는데, 여기에는 과학적인 근거가 있다. 이 ‘가늘게 뜨고 보기’는 물체에서 오는 빛다발을 극단적으로 좁히는 효과가 있다. 즉, 바늘 구멍을 통해서 보는 것과 비슷하다. 손가락 끝을 모아서 작은 구멍을 만들고 이를 통해 보면 퍼져 보이던 것이 나름 선명해짐을 느낄 수 있다. 근시 또는 원시의 경우 상이 퍼지는 이유는 물체의 한 점에서 출발한 빛이 다양한 경로([그림 9]에서 여러 파란색 선)를 통해 수정체에 도달하고 이를 수정체가 망막 앞이나 뒤에 상을 맺는 바람에 이들 빛살이 망막의 서로 다른 곳에 떨어지기 때문이다. 만약, 물체에서 오는 빛이 아주 좁은 빛살([그림 9]에서 파란색 선 한 개만 고려하자)을 통해서 온다면 본래 상이 맺히는 평면과 망막의 위치가 불일치하더라도 상이 꽤 선명히 생길 수 있다. 여기서 중요한 점은, 물체가 얼마나 멀리 있든, 수정체 렌즈가 규정하는 상의 위치(깊이)가 어디든, 비교적 선명한 상을 얻는다는 것이고, 뒤에서 언급할 피사계 심도^{depth of field}가 이론 상 매우 깊다는 것이다.

세상의 것이 이렇게 다 좋을 수 없으니 단점이 있기 마련이다. 확실한 단점은 광량이 아주 적어진다는 것, 물체가 어둡게 보인다는 점이다. 신호가 약하므로 어두운 곳에서 활용하기 어렵다. 아주 환한 곳에 있는 물체를 이미징하는 경우, 바늘구멍을 통해 상을 맺으면 초점심도^{focal depth/depth of focus} (아래 설명 참조)가 아주 길기에, 다양한 깊이의 물체 모두에 대한 훌륭한 상을 얻을 수 있다. 이것이 바늘구멍 사진기의 원리이고, 인터넷에 이에 대한 설명과 이를 이용해 얻은 멋진 상들을 찾을 수 있다 [8]. 사진기가 발명되기 전에 일부 화가들은 바늘구멍 상자(어두운 방^{camera obscura; chamber/room obscure/dark} [그림 10])를 이용해서 밑그림을 만들고 (그림 위에 놓은 반투명지를 놓고 베끼듯, 그냥 따라 그리면 모양이 나온다!) 원하는 곳에서 채색하였다고 한다. 이 바늘구멍 상자가 현대적 사진기의 선조 격이므로 카메라가 카메라로 불리게 되었다.

필자를 포함해 사진 찍기를 즐기는 사람들 대부분이 자동 카메라 (a.k.a. 똑딱이)가 알아서 설정해준 조건을 이용해 사진을 찍는다. 자동 카메라는, 찍는 사람이 겨냥한 방향에 있는 물체 중 어떤 것을 대상체로 판정하여 거기에 초점을 맞추고(자동 초점 기능), 광량을 판단해서 노출 시간을 정해준다 (물론 아닌 경우도 있다). 하지만, 항상 만족스럽거나 의도한 결과를 주지 않으므로 촬영 설정을 바꾸고 싶은 경우가 있다. 대표적인 설정 조건으로 노출 시간과 f/#^{f number}가 있다. 이들 모두 한 이미지 당 사용되는 광량을 조절하는 효과가 있지만 방법이 다르고, 쓰임새도 다르며, 반대급부가 다르다. 광량은 영상 취득에 가장 중요한 요소 중 하나로, 너무 많으면, 모두 하얗게 나와서 형체를 구분할 수 없다. 이는 카메라든 인간의 눈이든 비슷하다. 광량이 너무 많으면, CCD chip의 모든 픽셀(pixel = picture + cell)에서 광전자 수가 허용 최대치를 넘기게 되고, ‘최대 신호값(8 bit이면 255)’에 도달함으로써 영상 전체가 하얘진다. 망막의 경우, 시각세포의 신호가 포화되어 아무것도 제대로 볼 수 없고, 엄청난 눈부심을 경험한다. 반면, 빛 알이 너무 적으면, 형체를 구현할 만한 빛 알이 없으니 모양을 만들 수, 볼 수 없다.

노출 시간은 한 프레임을 찍을 때 셔터(홍채-동공)을 여닫는 시간을 가리키는데, 시간 간격을 조절하여 광량을 조절한다. 물체가 움직이는 경우에 노출시간을 길게 하면 한 이미지에 변화된 다른 그림을 겹쳐 인쇄한 꼴이므로 제대로 된 영상을 얻을 수 없다. 충분히 빠르지 않은 카메라로 고속 주행하는 물체를 찍으면 발생하는 일이다. 노출시간을 짧게 하면 움직임을 따라갈 수도 있겠지만, 광량이 줄어든다.

f/#는 \({f}\)/\({D}\)로 정의되는데 여기서 \({f}\)는 렌즈의 초점 거리, \({D}\)는 입사광 조리개의 지름이다. 이는 셔터를 열어서 받아들이는 빛의 시야각, 개구수(NA)와 관련된 양이다. f/# 값이 작으면, NA가 크다고 볼 수 있다. f/1.4, f/2.0, f/2.8 등 f/# 값이 조리개 옆에 붙어 있는 것을 볼 수 있는데, #는 셔터 크기(길이)의 축소비율과 관계가 있다 [그림 11]. 1.4  \(\sim \sqrt 2\) 를 의미하여 이를 셔터 넓이로 환산하면 \(\left( \frac{1}{\sqrt 2} \right)^2 = \frac{1}{2}\) 가 되어, 받아들이는 시야 넓이가 ‘최대치’의 절반이 됨을 의미한다. 넓게 열면 빛을 잘 받아 밝고 선명한 영상을 얻는 데 도움이 된다. 하지만, 조리개가 넓어지면 초점심도에 관련된 단점도 있다. 위에 바늘구멍 사진기와 정반대의 경우이다.

그럼 NA가 어떻게 피사체 심도, 초점 심도에 영향을 주는지 살펴보자. 자세하고 정확한 이론은 참고문헌[9]으로 미루고 결과를 바로 가져와서 이야기하겠다. 한 점에서 나온 빛이 상을 맺을 때 깊이 방향으로 퍼지는 정도가 다음과 같이 주어진다.

\(\Delta z \sim \frac{2 n’ M^2 \lambda}{NA^2}\)

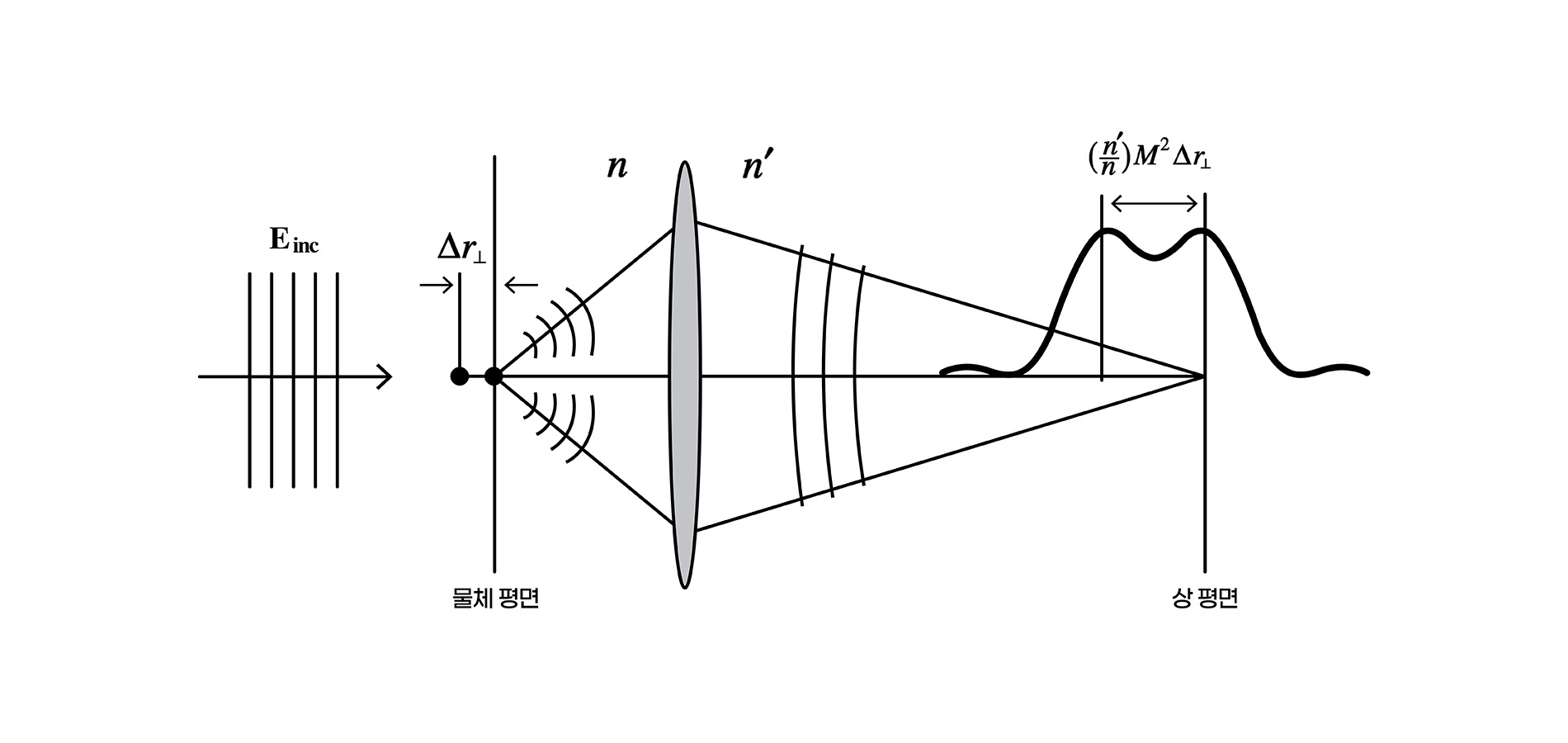
여기서 \(\Delta z\) 가 피사체 심도이다. 이때 깊이 방향으로 \(\Delta r_\perp\) 떨어진 두 점을 구별하려면, \(\Delta z \le M_L \Delta r_\perp = (\frac{n’}{n})M^2 \Delta r_\perp\)을 만족해야 한다. 이 식에서 \({n}\), \({n’}\) 은 각각 물체가 놓인 곳의 매질과 상이 생기는 곳의 매질의 굴절률이고, \({M}\), \({M}_{L}\) 은 각각 횡방향, 종방향(깊이 방향) 배율이다 [그림 12].

구별 가능한 최소 깊이 차이는 \(\Delta r_{\perp} = \frac{2 n \lambda}{NA^2}\) 이 되고, 이것이 초점 심도이다. 여기에서 보는 바와 같이, NA가 크면 , \(\Delta z\), \(\Delta r_{\perp}\) 가 급격히 감소하여 정확한 대상체에서 앞뒤로 조금만 벗어나기만 하면 금방 영상이 흐려지고 퍼진다. 시야에서 특정 거리에 있는 하나의 피사체만 강조하고 싶다면 이를 장점으로 활용할 수 있다. 뒷배경은 흐릿하고 관심 피사체만 선명한 사진을 얻을 수 있다. 반대로 NA가 작으면, 정확한 대상체에서 앞뒤로 많이 벗어나도 꽤 좋은 영상을 얻을 수 있다. 바늘구멍 사진기 경우처럼 깊게 찍을 수 있지만, 영상은 상당히 어두워진다. 광학적 원리만 놓고 보면 우리 눈도 깊이가 다른 물체를 파악하는 데 제약이 있는 것은 마찬가지라고 할 수 있다. 앞을 골똘히 집중해서 보면 뒤(먼 곳)를 못 보고, 먼 곳을 멍하니 보면 가까운 데를 못 보는 것은 당연하다.

시각에 대한 얘기를 신나게 풀다 보니, 어느덧 모니터를 몇 시간째 보고 있는 줄 잊고 있었다. 별로 밝지 않은 연구실에서 가까운 모니터만 집중하는 게 근시를 조금 더 강화했겠다는 생각이 들어 눈도 이제 쉬게 해줘야겠다.