5월의 퍼즐에 참여해주신 모든 분들께 감사드립니다!
5월의 퍼즐에 참여해주신 분 중 정답과 함께 좋은 풀이를 보내주신 정찬영님께
HORIZON에서 문화상품권을 전달드릴 예정입니다.
주머니 안이 넉넉하다고 가정했기 때문에, 이 문제는 둘레 6cm 고리에 해당 물체를 통과시킬 수 있는지 묻는 것과 같다.
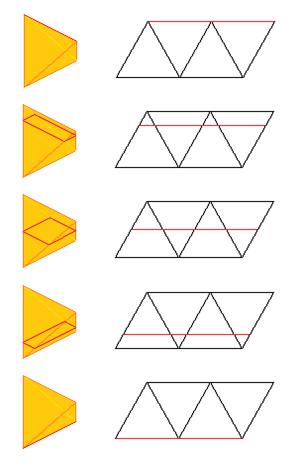
1. 한 모서리의 길이가 3cm인 정사면체를 생각하자. 이 경우 정사면체를 모서리로 똑바로 세운 다음 위쪽 모서리부터 지면과 평행하게 내려오면 된다. 정사면체의 전개도를 펼치면 정삼각형 4개가 모인 평행사변형이 되기 때문에 고리가 통과하는 과정을 전개도에 옮기면 고리가 계속 6cm를 유지하고 있음을 알 수 있다.
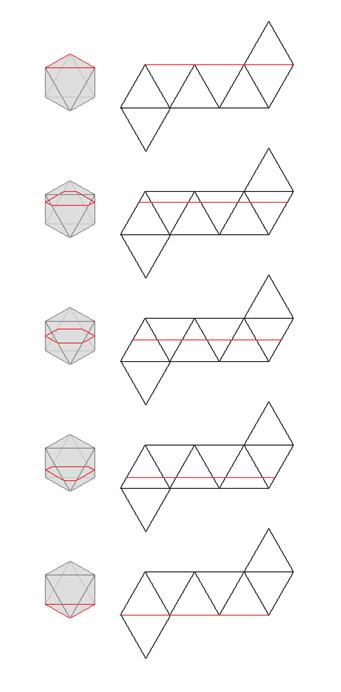
2. 한 모서리의 길이가 2cm인 정팔면체를 생각하자. 이 경우 정팔면체의 한 면이 바닥과 평행하게 놔두고 위쪽 면 정삼각형부터 시작해 지면과 평행하게 내려오면 된다. 정팔면체의 전개도를 펼치면 고리가 통과하는 부분이 정삼각형 6개가 모인 평행사변형이 되기 때문에 통과하는 과정을 전개도에 옮기면 고리가 계속 6cm를 유지하고 있음을 알 수 있다.
보너스 문제
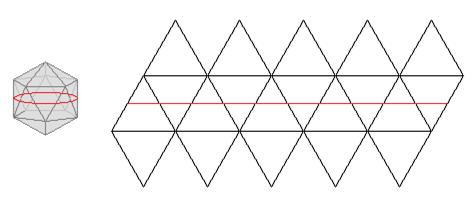
한 모서리의 길이가 1cm인 정이십면체의 경우 꼭짓점을 기준으로 바닥에 세우면 위아래 두 오각뿔과 중앙 몸통으로 나눌 수 있다. 위쪽 오각뿔의 밑면에서 아래쪽 오각뿔의 밑면으로 고리를 움직일 때를 전개도에 옮기면 고리의 길이가 5cm를 유지함을 알 수 있다.
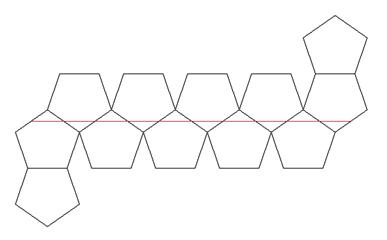
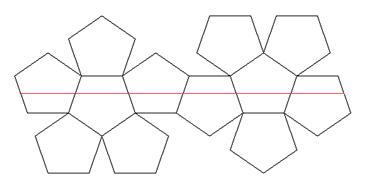
한 모서리의 길이가 1cm인 정십이면체의 경우 (정팔면체처럼) 위아래에 면을 놓았을 때, 다음 그림과 같은 전개도를 생각하면 고리의 길이가 5φcm로 약 8.09cm가 되어 불가능한 것으로 생각이 된다.
그러나 (정이십면체처럼) 위아래에 꼭짓점을 놓을 때 다른 전개도를 생각하면 고리의 길이가 (3+3φ)cm로 약 7.85cm가 되어 둘레 8cm의 고리가 통과할 수 있게 된다.
다음은 5월의 정답자로 선정된 정찬영님의 해설입니다.
모든 정다면체는 항상 각각의 꼭짓점/모서리/면에 대하여 대칭성을 가지고 있다. 즉, 정다면체를 이루는 하나의 꼭짓점/모서리/면은 다른 꼭짓점/모서리/면에 비해 특별하지 않으며, 적절한 회전을 통해 한 꼭짓점/모서리/면을 다른 꼭짓점/모서리/면으로 겹칠 수 있다. 꼭짓점/모서리/면 대칭성이 있다는 말은, 꼭짓점/모서리/면부터 넣기 시작했을 때 단면 둘레의 최댓값이 최소를 이룰 가능성이 있다는 뜻이기도 하다. x=a에 대해 대칭인 함수 y=f(x)가 x=a 근방에서 볼록하거나 오목한 모양을 이루며 f(a)를 극값으로 가지는 것과 같은 이치이다. (x=a 근방에서 상수함수일 수도 있으나, 이번 퍼즐에서는 고려하지 않아도 된다.)
(0)을 예로 들어보자. 초록색 경로가 이 정다면체에 대한 대칭성을 가지고 있기 때문에, ‘경로를 따라 진행하는 평면이 정다면체를 통과하며 만들어낸 둘레의 최댓값’이라는 함수는 초록색 경로에서 극값을 가질 것이고, 이로부터 조금 벗어난 두 주황색 경로에서는 극값을 가지지 않을 것이다. 극점은 극대 또는 극소를 가질 수 있으므로 일부 대칭적인 경로에서는 극댓값이 나오겠지만, 꼭짓점/모서리/면대칭 경로 중 극솟값이 나오는 것도 있을 것이라고 기대할 수 있다. 이제 이 사실을 바탕으로, 각 정다면체를 꼭짓점/모서리/면부터 주머니에 집어넣는 경우를 살펴보자.
먼저 정사면체를 생각해보자.
가장 쉽게 떠올릴 수 있는 방법은 (1)과 같이 한 꼭짓점부터 시작해서 주머니에 넣는 방법이다. 입구의 둘레의 길이가 6cm이므로 단면이 만드는 삼각형의 한 변의 길이가 2cm가 되는 부분에서 막히게 된다. 한 면부터 주머니에 넣는 방법도 이미 넣을 때부터 둘레가 9cm로, 주머니 입구 둘레 6cm를 넘긴다. 즉, 꼭짓점/면 대칭성으로는 정사면체를 주머니에 넣는 것이 불가능하다는 것을 어렵지 않게 알 수 있다.
나머지 방법은 (2)같이 한 모서리부터 시작하여 입구를 통과시키는 방법이다. 정사면체의 한 변의 길이가 3cm이기 때문에 언뜻 보면 (2a)처럼 주머니에 넣기 시작할 때부터 주머니 입구가 꽉 찬 상태이므로 통과하기 어려울 것처럼 보이지만, 실제로는 (2b)처럼 단면이 만드는 사각형의 둘레의 길이가 정확히 6cm를 유지하며 통과할 수 있게 된다.이 상황을 알아보기 쉽도록 (2b)를 전개하여 평면으로 나타내면 (3)과 같은 그림이 나온다. 파란색으로 표시한 부분이 주머니를 통과하는 사각형의 둘레이다. 그런데 (3)의 모양은 평행사변형이므로, 위나 아래로 움직여도 파란색으로 표시한 부분의 길이는 6cm로 일정함을 알 수 있다. 따라서, 정사면체는 모서리-모서리 축으로부터 최소의 단면 둘레가 나온다.
정팔면체도 같은 방법으로 접근해보자.
정사면체의 경우와 마찬가지로, (4)와 같이 한 꼭짓점부터 시작해서 주머니에 넣는 방법이 가장 먼저 떠오른다. 그러나 역시 마찬가지로 단면이 만드는 정사각형의 한 변의 길이가 1.5cm가 되는 부분에서 막히므로, 꼭짓점 대칭을 이용한 방법으로는 정팔면체를 주머니에 넣을 수 없다. 한 모서리부터 시작하여 맞은편 모서리까지 통과하는 방법도, (5)와 같이 둘레의 길이가 4*\(\sqrt{3}\) cm 인 단면을 통과해야 하므로 둘레가 6cm인 주머니 입구를 통과할 수 없다.
그러면 이제 남은 방법은 한 면에서 시작해서 맞은편 면까지 통과하는 방법이다. 이번에도 역시 신기하게도 주머니를 통과하는 동안 단면 둘레의 길이가 정확히 6cm를 유지하며 통과된다. (6b)를 전개한 (7) 그림을 보면 정사면체의 경우와 마찬가지로 전개된 도형이 평행사변형이므로, 파란색 부분(단면의 둘레) 길이가 6cm를 유지하면서 아래로 내려간다. 따라서 정팔면체는 면-면 축으로부터 최소의 단면 둘레가 나온다.정십이면체와 정이십면체도 꼭짓점/모서리/면 대칭축을 따라 통과시키는 방법을 조사하면 최소의 둘레로 주머니 입구를 통과할 수 있는 경우를 찾을 수 있다.
먼저 정십이면체의 경우는 (8)과 같다. 단면 둘레의 최댓값은 면-면 축을 따라 통과시킬 때 5*(1+\(\sqrt{5}\))/2≈8.090cm, 모서리-모서리 축을 따라 통과시킬 때 \(2+2\sqrt{5+2\sqrt{5}}\)≈8.155cm, 꼭짓점-꼭짓점 축을 따라 통과시킬 때 3+3*(1+\(\sqrt{5}\))/2≈7.854 cm이다. 따라서 한 변의 길이가 1cm인 정십이면체는 둘레가 8cm인 주머니 입구에 넣으려면 꼭짓점-꼭짓점 축을 따라 넣으면 된다. (사실 둘레의 길이가 3+3*(1+\(\sqrt{5}\))/2≈7.854 cm만 되어도 가능하다.)정이십면체는 (9)와 같이 통과시킬 수 있다. 면-면 축을 따라 통과시킬 때 3*(\(\sqrt{3})\)≈5.196cm, 모서리-모서리 축을 따라 통과시킬 때 2+2*(\(\sqrt{3})\)≈5.464cm, 꼭짓점-꼭짓점 축을 따라 통과시킬 때 5cm라는 단면의 최대 둘레 길이를 갖는다. 그러므로 한 변의 길이가 1cm인 정이십면체는 꼭짓점-꼭짓점 축을 따라 넣으면 둘레가 5cm인 입구를 통과할 수 있다.