4월의 퍼즐에 참여해주신 모든 분들께 감사드립니다!
4월의 퍼즐에 참여해주신 분 중 정답과 함께 좋은 풀이를 보내주신 박종훈님께
HORIZON에서 준비한 선물을 전달드릴 예정입니다.
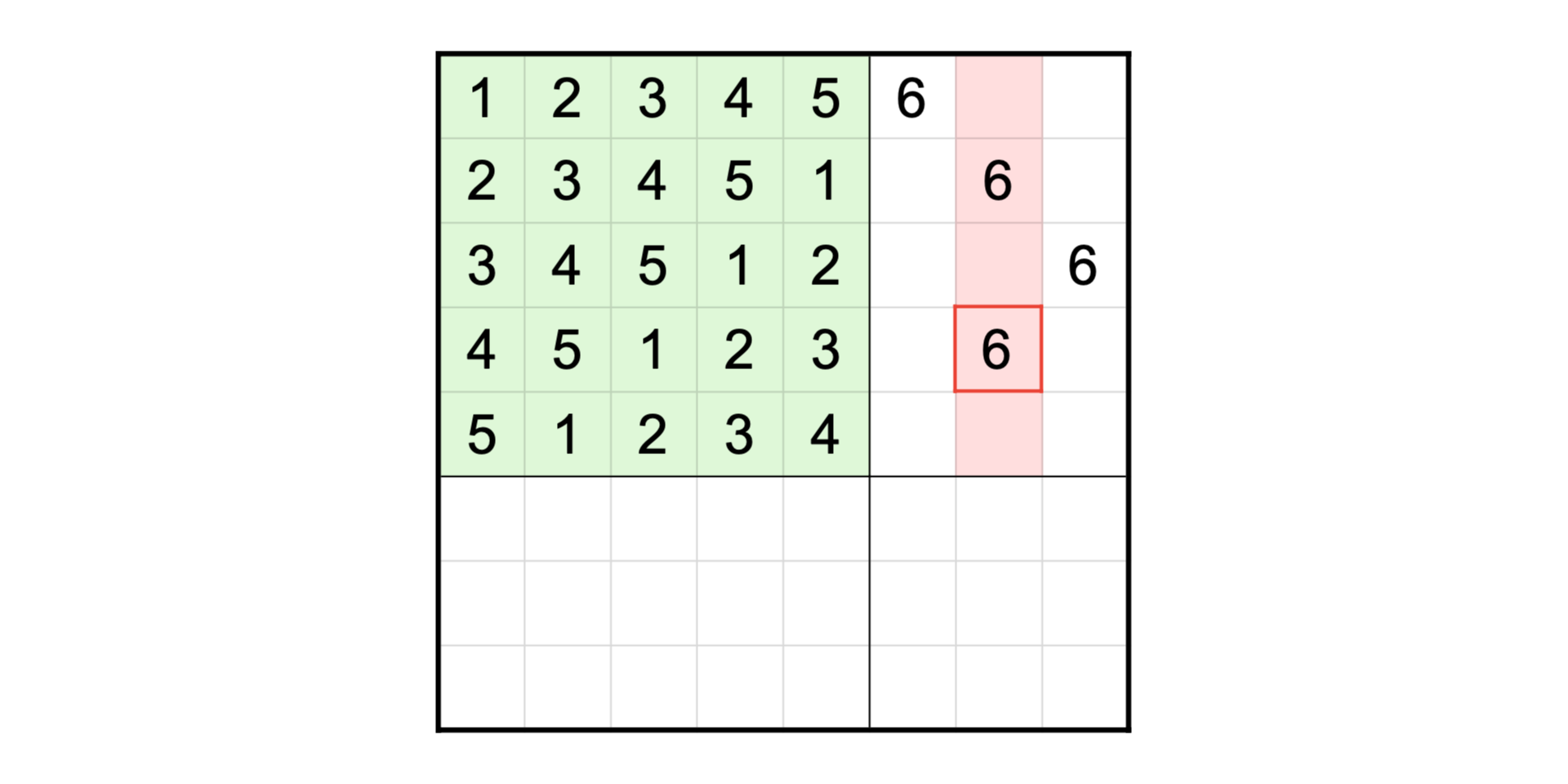
라틴 방진은 행과 열의 순서를 바꿔도 라틴 방진이므로, 행과 열의 순서를 적절히 바꿔서 1~M으로 채워진 M×M 라틴 방진을 왼쪽 위에 고정시켰다고 가정하고 문제를 생각해 보자. 전체 정사각형을 다음과 같이 M×M, M×(N-M), (N-M)×M, (N-M)×(N-M) 네 개의 부분 격자로 쪼개서 생각할 것이다.
먼저 2M > N인 경우를 살펴보자. 첫 M개 행에 수 M+1을 어떻게 배치해야 하는지 확인해 볼 것이다. 왼쪽 M×M 격자에는 1부터 M까지의 수만 들어가므로 오른쪽 M×(N-M) 격자에 수 M+1을 M개 행만큼 채워야 한다. 하지만 놓을 수 있는 열의 위치는 N-M으로 M개보다 작다. 따라서, 비둘기집의 원리에 의해 어떤 열에는 M+1이 둘 이상 배치되어야 하고, 라틴 방진을 만들 수 없다.
그렇다면 2M ≤ N인 경우에는 항상 라틴 방진을 품은 라틴 방진을 만들 수 있을까?
일단 M×M 격자를 채우고, 추가로 우측 M×(N-M) 격자에서 행을 회전해 가면서 M+1~N을 채우면 첫 M개 행에 1부터 N까지의 수가 중복 없이 들어가게 된다. 이를 M×N 라틴 직사각형이라고 부른다. 어떤 M×N 라틴 직사각형이든 N-M개의 열을 추가해서 라틴 방진으로 확장할 수 있음이 알려져 있으므로, 2M ≤ N인 경우는 항상 라틴 방진을 품은 라틴 방진을 완성할 수 있다. (증명은 필자의 블로그에 소개되어 있다.)
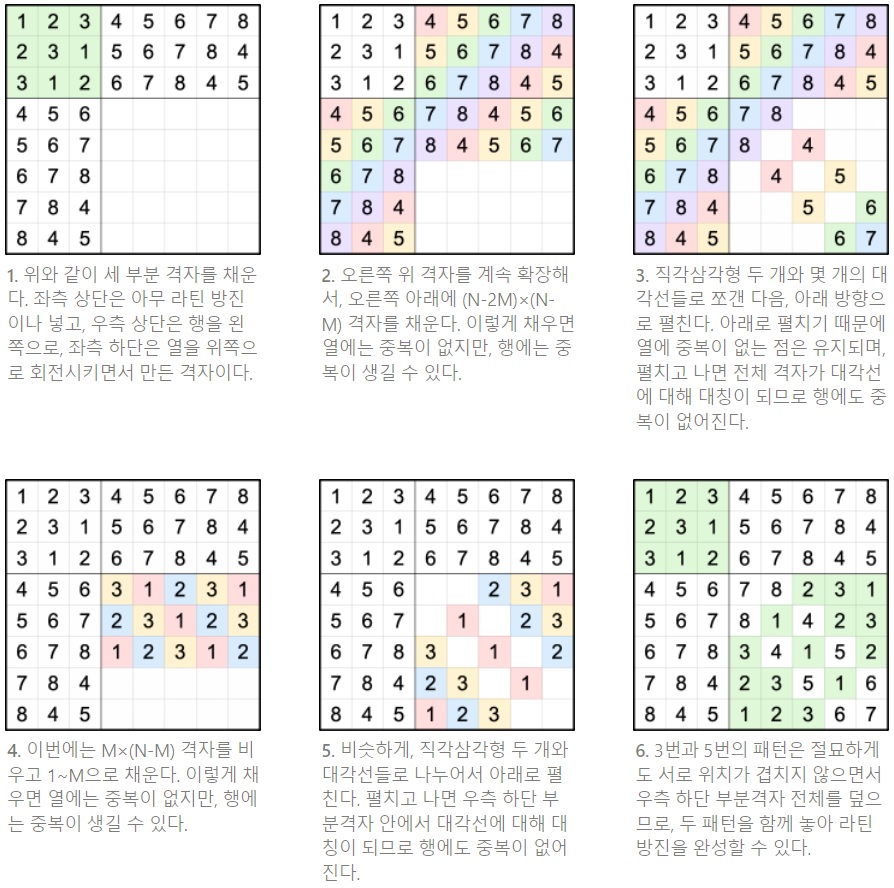
물론 위와 같이 증명할 수도 있지만, 위 풀이는 직접적으로 라틴 방진을 품은 라틴 방진을 구성하는 방법을 제시해 주지는 않는다. 실제로 구성하는 방법은 여러 가지가 있겠으나 아래에 소개할 것은 KPP 이충명님이 찾은 방법을 필자 나름대로 재해석한 풀이이다.
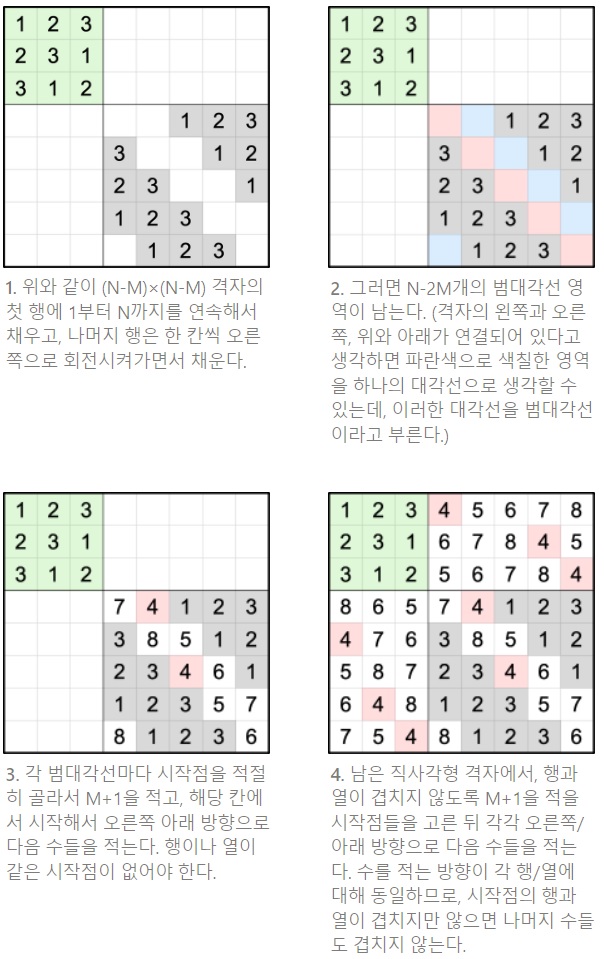
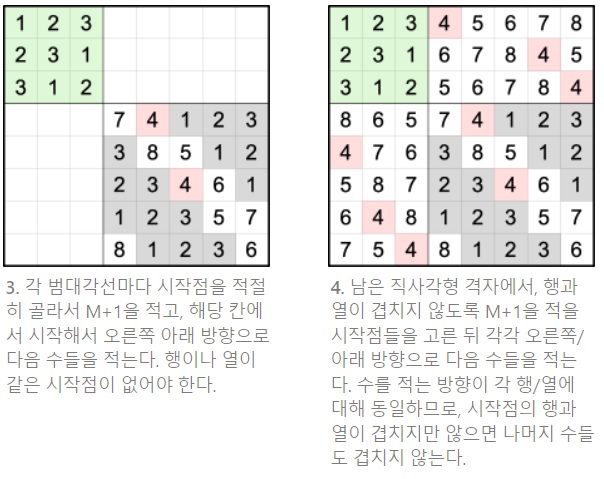
추가로 KPP 안진후님의 풀이도 소개한다. M×(N-M) 직사각형 영역부터가 아니라, 우측 하단 (N-M)×(N-M) 격자부터 채우는 방법이다.
3번 과정에서 대각선마다 겹치지 않게 시작점을 고르는 방법은 독자를 위한 연습문제로 남긴다. N-2M이 홀수일 때와 짝수일 때를 나눠서 처리해야 함에 주의하자.
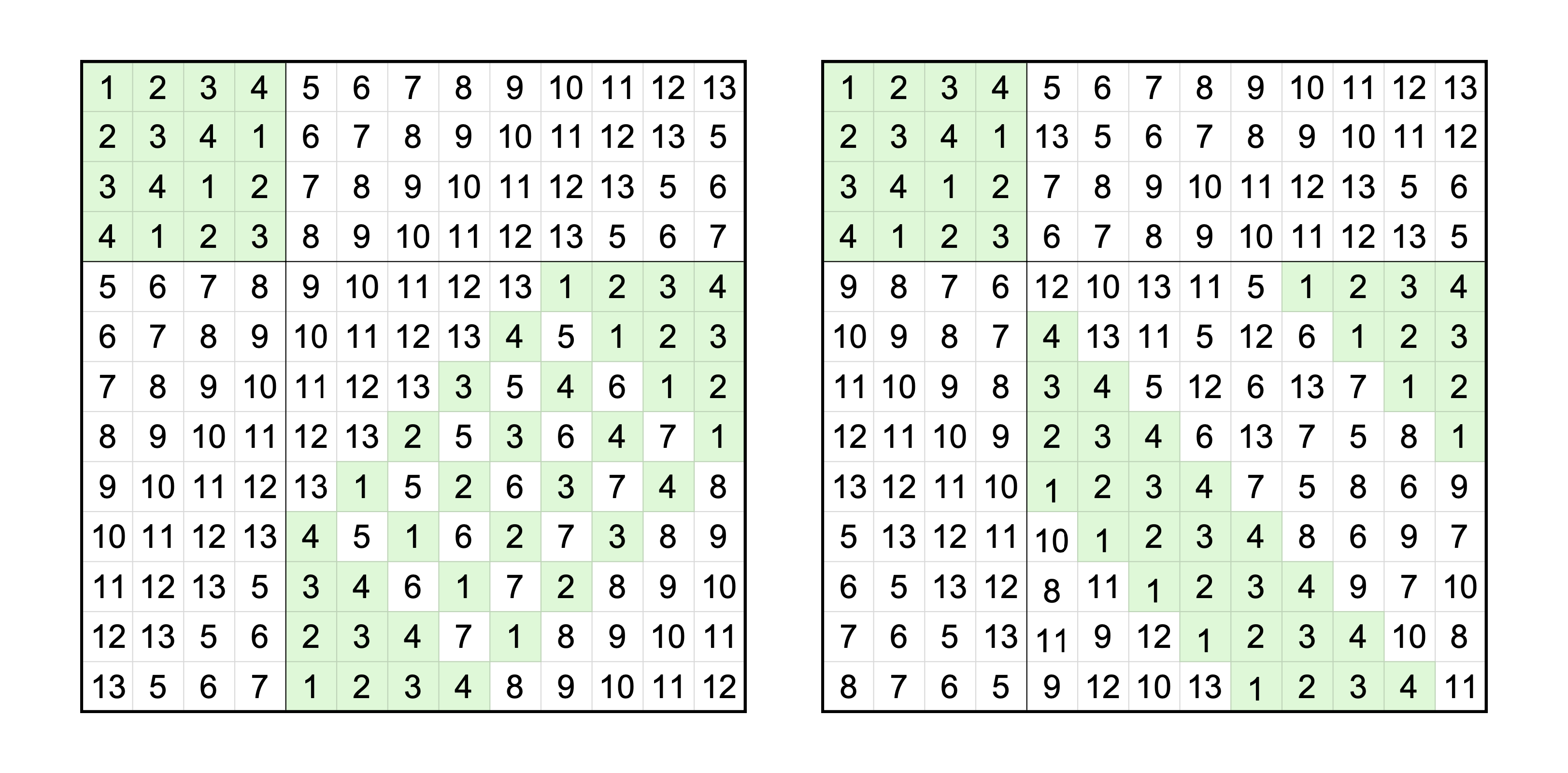
아래의 두 그림은 위에서 소개한 두 가지 풀이에 따라 만든, 4×4 라틴 방진을 품은 13×13 라틴 방진이다.
다음은 4월의 정답자로 선정된 박종훈님의 해설입니다.
먼저, 일반성을 잃지 않고 MxM 라틴 방진을 품은 NxN 라틴 방진에서, MxM 라틴 방진은 항상 맨 왼쪽 위에 있다고 가정할 수 있습니다. 그 외의 위치에 있을 때 MxM 라틴 방진을 포함한 행과 열들을 맨 왼쪽 위의 행과 열들과 교환해도 여전히 라틴방진이기 때문입니다. 또한, 마찬가지로 일반성을 잃지 않고 MxM 라틴방진에는 1~M으로만 구성되어있다고 가정합시다.
1. 만들 수 없습니다. 5×5 라틴방진이 1~5행, 1~5열에 있을 때 1~5행의 6열에 해당하는 5칸에는 6~8 만 올 수 있는데, 3개의 수로 같은 열의 5칸을 채울 수 없으므로 라틴 방진을 만드는 것이 불가능합니다.
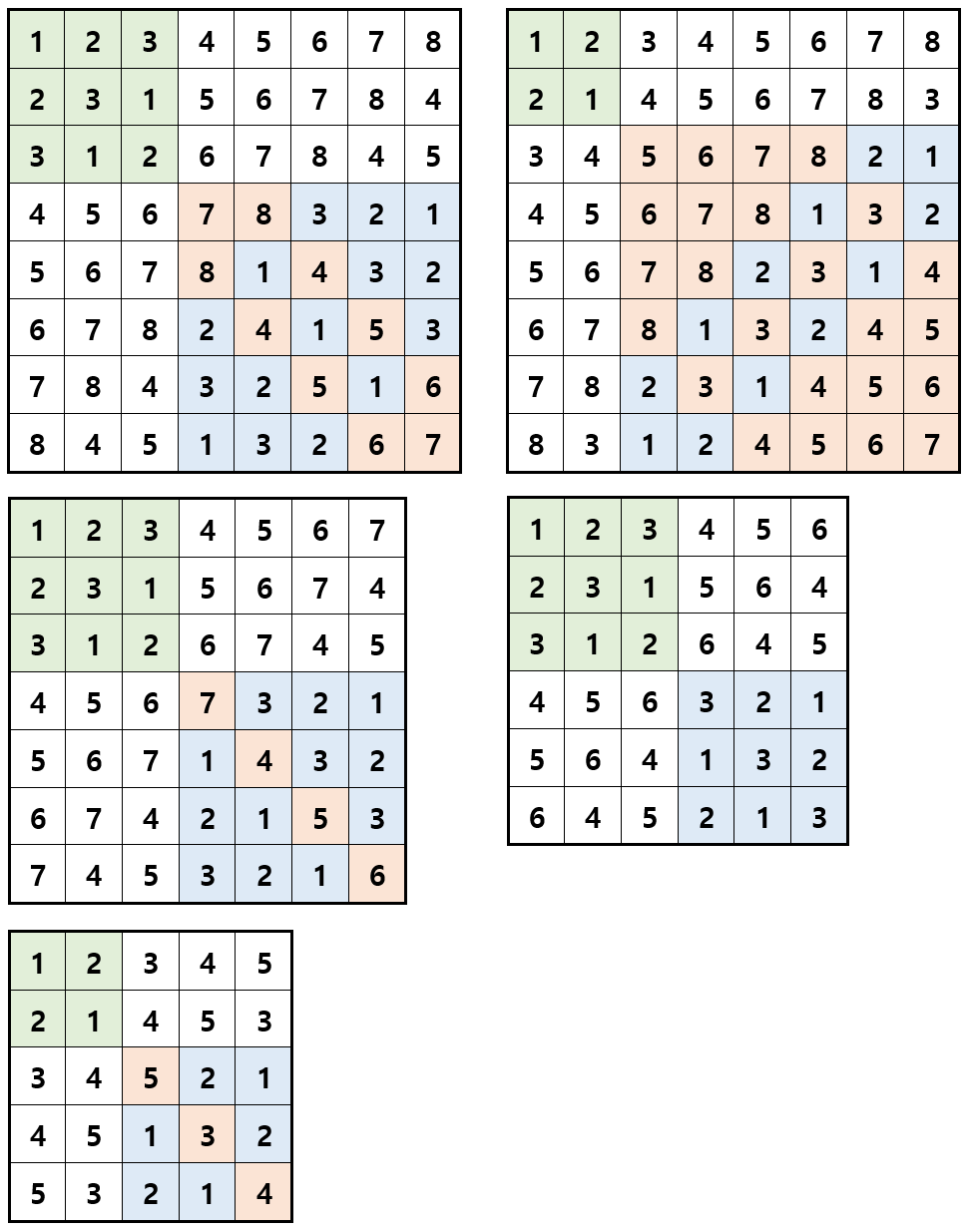
2. 아래와 같이 가능합니다.
1 2 3 4 5 6 7 8
2 3 1 5 6 7 8 4
3 1 2 6 7 8 4 5
4 5 6 7 8 3 2 1
5 6 7 8 1 4 3 2
6 7 8 2 4 1 5 3
7 8 4 3 2 5 1 6
8 4 5 1 3 2 6 7
3. 1번 문제에서 불가능한 이유로부터 유추해보자면, M칸에 N-M개의 숫자를 채워넣을 수 있어야 하므로 M > N-M => M > N/2 이면 불가능 하고 그 외의 경우인 M <= N/2 이면 가능할 것 같습니다.
4. (이미지와 함께 봐주세요)
(1) 왼쪽 위에 초록색 구역에 먼저 MxM 라틴 방진을 자유롭게 배열합니다. (ex. 본문과 같이 한칸씩 회전시키며 123 / 231 / 312)
(2) 오른쪽 위 하얀색 Mx(N-M) 크기의 구역에 행별로 M+1 ~ N의 수를 한 칸 씩 회전시키며 배열합니다. (ex. 45678 / 56784 / 67845)
(3) 왼쪽 아래 하얀색 (N-M)xM 크기의 구역에는 (2)에서 배열한 수와 (왼쪽 위에서 오른쪽 아래로의)대각선에 대해 대칭이되도록 배열합니다. (456 / 567 / 674 / 745)
(4) 오른쪽 아래 (N-M)x(N-M) 크기의 구역은 두 개의 구역으로 분리할 수 있습니다. 구역의 (1, N-M+1) 좌표 칸을 파란색으로 칠하고 나머지 칸들을 체스판 배열로 파랑, 빨강으로 칠한 뒤에 오른쪽 위와 왼쪽 아래의 MxM 직각삼각형을 파란색으로, 왼쪽 위와 오른쪽 아래의 (N-2M)x(N-2M) 크기의 직각삼각형을 빨간색으로 칠하면 그림과 같이 파랑, 빨강 구역으로 구분됩니다. 이 때 파랑 구역은 오른쪽 위에서 왼쪽 아래 방향으로 1, 2, … N, N+1 .. 을 채워주고, 빨강 구역은 왼쪽 위에서 오른쪽 아래 방향으로 2M+1, 2M+2, … N, M+1, … 을 채워주면 항상 라틴 방진이 만들어집니다.