2022년 아벨상은 위상수학, 기하학, 동역학 등 여러 분야에서 중요한 업적을 남긴 데니스 설리반에게 돌아갔습니다. 설리반은 다양체의 PL구조의 유일성, 리프쉬츠 구조의 존재성, 위상적 공간의 국소화, 유리호모토피이론, 초끈위상학, 클라이니안군론 등 기하, 위상의 다양한 주제에서 중요한 질문에 대한 해답을 제시했을 뿐 아니라 새로운 관점을 제시함으로써 다양한 분야의 발전에 큰 공을 세웠습니다. 이 글에서는 그중에서도 설리반의 복소동역학에 관련된 업적을 소개하려 합니다.
설리반이 많은 연구를 했던 클라이니안군론과 복소동역학 모두 아름다운 프랙탈 그림을 연구하는 분야로도 유명합니다. 프랙탈이란 아무리 작은 부분을 고르더라도 확대하면 원래 모습과 동일한 모양을 가지는 도형을 의미합니다.
1.복소동역학
동역학
동역학계를 생각하는 가장 큰 동기는 시간이 지남에 따라 현상이나 대상이 어떻게 변하는지를 이해하는 것입니다. 현대 수학에는 다양한 동역학계의 모형이 있지만, 그중에서 우리는 \(f:X\to X\) 라는 간단한 수식으로 정의되는 동역학계를 생각해 봅시다. \(X\) 는 공간이고 \(f\)는 \(X\) 에서 자기 자신으로 대응되는 함수입니다. \(X\)의 모든 원소 \(x\) 는 공간 \(X\) 에서의 위치를 나타낸다고 생각합시다. 우리는 이 함수 \(f\)를 \(x\in X\) 라는 지점에 있는 물질을 1 초 후에 \(f(x)\) 라는 지점으로 옮기는 법칙으로 생각할 것입니다. 이 함수 \(f\)의 정의역과 공역이 \(X\)로 동일하기에 함수 \(f\) 를 \(X\)라는 공간에 반복해서 합성시킬 수 있습니다. \(n\)번 반복 합성한 함수 \(f^{\circ n}:X \to X\) 는 공간 \(X\)의 \(x\)라는 위치에 있는 물질이 \(n\) 초 후에 \(f^{\circ n}(x)\)로 간다는 것을 알려줍니다.
복소동역학: 2차 다항식
복소동역학은 복소구조를 가지는 공간에서 정의된 동역학계를 연구하는 분야입니다. 그 중 가장 오래된 주제는 리만 구 \(\hat{\mathbb{C}}\) 에서 정의된 복소유리함수rational functions with complex coefficients를 반복 합성하여 얻어지는 동역학계입니다. 그중에서도 가장 간단한 2차 다항식의 동역학을 살펴보겠습니다.
함수 \(f:{\mathbb{C}}\to{\mathbb{C}}\) 가 \(f(z)=z^2\)로 주어졌다고 가정해봅시다. 함수가 간단하기 때문에 우리는 \(n\)번 반복 합성한 함수 \(f^{\circ n}(z)=z^{2n}\) 를 정확하게 쓸 수 있습니다. 시간이 많이 흘렀을 때의 궤적 \(\{f^{\circ n}(z)\}\)을 다음과 같이 세 가지로 분류할 수 있습니다.
(i) |z|<1 인 경우: 궤적 \(\{f^{\circ n}(z)\}\) 는 0으로 수렴합니다.
(ii) |z|>1 인 경우: 궤적 \(\{f^{\circ n}(z)\}\) 는 \(\infty\) 로 발산합니다.
(iii)|z|=1 인 경우: \(|z^n|=1\) 이므로 궤적 \(\{f^{\circ n}(z)\}\) 는 계속 단위원 \(S^1=\{z \in {\mathbb{C}} ~|~ |z|=1\}\) 에 머무릅니다. 또한 \(f\) 는 \(S^1\) 을 보존하기 때문에, \(f(S^1)=S^1\), 정의역과 공역을 \(S^1\)으로 제한한 동역학계 \(f|_{S^1}:S^1\to S^1\) 을 생각할 수 있고, 이는 \(x\) 축과의 각도 \(\theta\) 를 2배로 만드는 함수가 됩니다, \(f(e^{\theta i})=e^{2\theta i}\).
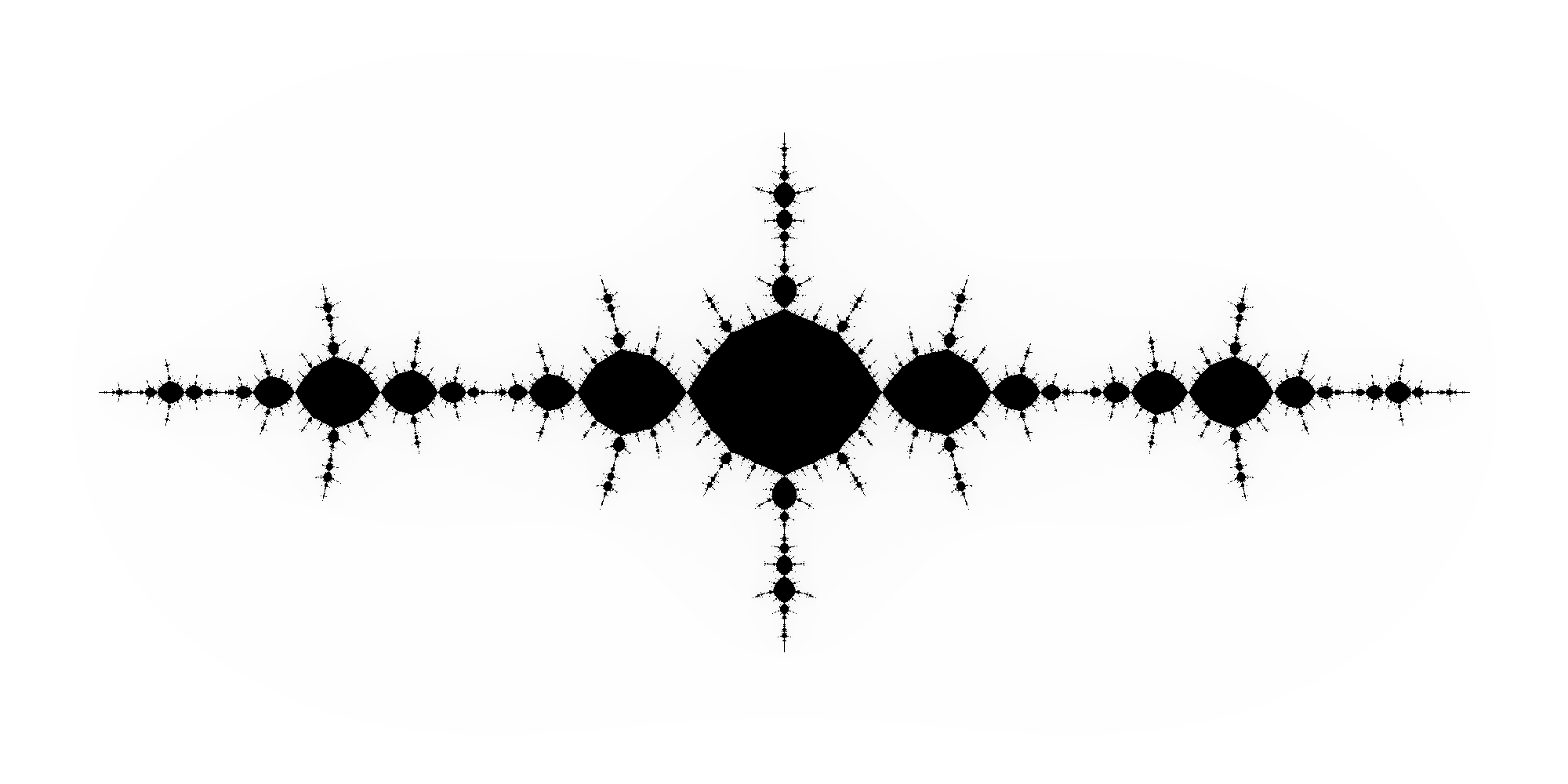
다음으로 \(f(z)=z^2-1\)를 생각해봅시다. 이번에는 n번 합성한 함수 \(f^{\circ n}(z)\)의 정확한 수식 표현으로부터 궤적 \(\{f^{\circ n}(z)\}\)을 설명하기가 어렵습니다. 하지만 \(f(0)=-1\), \(f(-1)=0\) 으로 부터 우리는 \(\{0,-1\}\) 이 주기가 2인 순환periodic cycle with period 2을 이룬다는 것을 알 수 있습니다. 더 정확히는 \(\{0,-1\}\)은 주변의 점들을 끌어당기는 순환이 되는데, \(z^2\) 의 경우와 비슷하게 다음과 같이 세 가지 경우로 분류할 수 있습니다. [그림2-a]를 봅시다.
(i) \(z\) 가 검은색 원판 내부에 있는 경우: 궤적 \(\{f^{\circ n}(z)\}\) 는 주기적 순환 \(\{0,1\}\) 으로 수렴합니다.
(ii) \(z\) 가 바깥 흰색 영역에 있는 경우: 궤적 \(\{f^{\circ n}(z)\}\) 는 \(\infty\)로 발산합니다.
(iii) \(z\) 가 검은 영역의 경계 \(X\) 에 있는 경우: 궤적 \(\{f^{\circ n}(z)\}\) 는 \(X\)에 머무릅니다.
두 경우 다 (i),(ii)에 해당하는 점들을 모아놓은 집합을 파투집합, (iii)에 해당하는 점들을 모아놓은 집합을 줄리아집합이라고 합니다. 특히 \(z^2-1\)의 경우 줄리아집합이 바실리카 형식의 건물과 닮아서 바실리카 줄리아집합이라고 부릅니다.
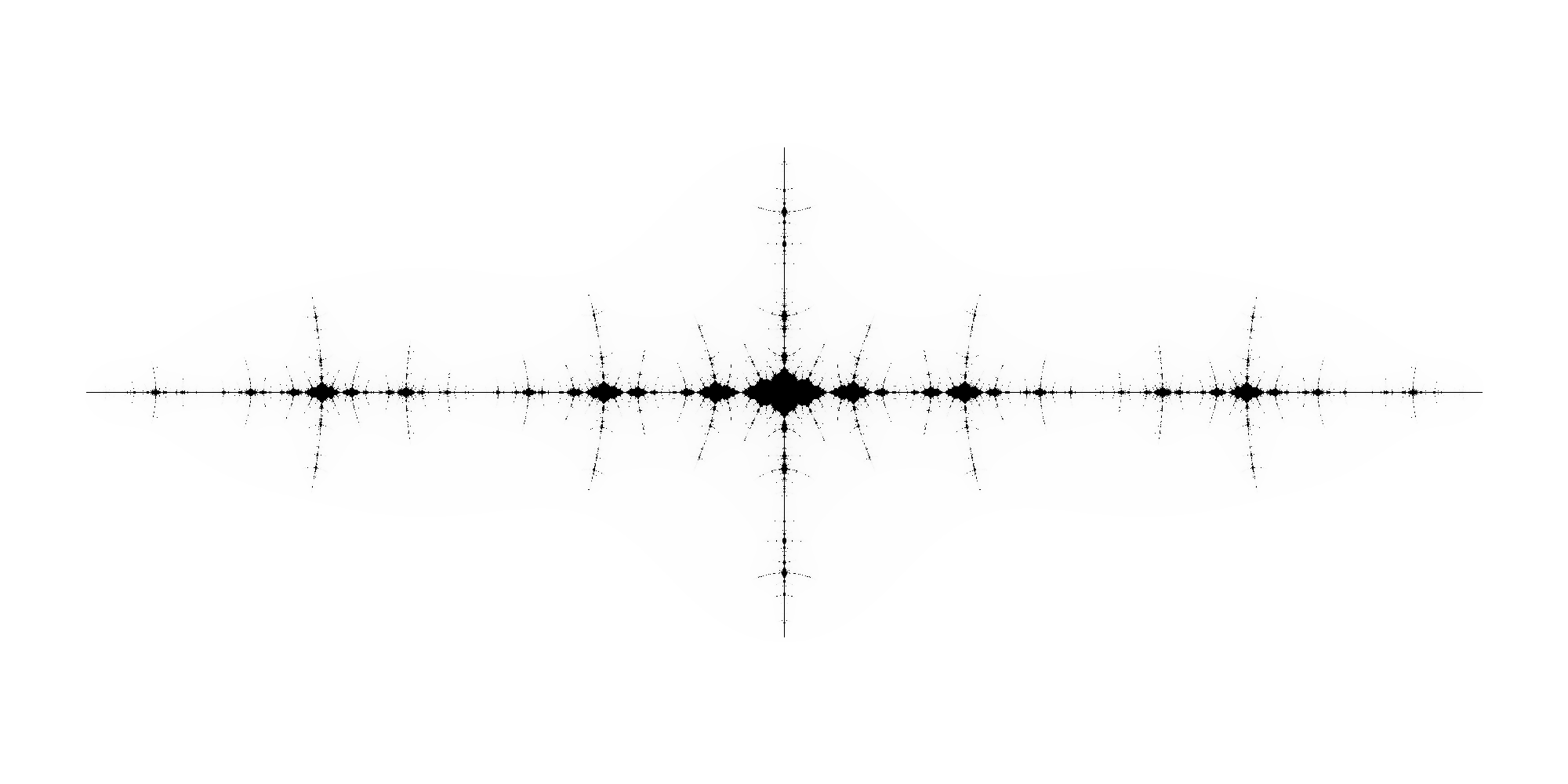
이제 임의의 복소수 \(c\)에 대해서 이차 다항식 \(f_c(z)=z^2+c\)를 생각해봅시다. 각각의 \(f_c(z)\)에 해당하는 줄리아집합 \(\mathcal{J}_c\)를 정의할 수 있습니다. 줄리아집합 \(\mathcal{J}_c\) 가 연결집합이 될 필요충분조건은 0의 궤적 \(\{f_c^{\circ n}(0)\}\) 이 유계임을 보일 수 있습니다. 복소평면을 매개변수 \(c\)들을 모아놓은 공간으로 생각하고, 그중에서 줄리아집합 \(\mathcal{J}_c\) 가 연결집합인 \(c\)들을 모아놓은 집합을 망델브로집합이라고 합니다. ([그림2-b])
망델브로집합의 위상적, 기하학적 성질을 밝히는 것은 복소동역학에서 가장 인기가 많은 주제 중 하나입니다. 그중 망델브로집합이 국소적으로 연결되어있음Mandelbrot set is Locally Connected, MLC 추측을 보이는 것은 중요한 미해결제로 남아있습니다.
2.재정규화
복소동역에서의 재정규화는 특히 앞서 설명한 MLC 추측을 해결하기 위한 방법으로서 발전을 해왔습니다. 간단히 말하자면 재정규화란 작은 부분에 유도되는 동역학계를 의미하는데, 설리반은 재정규화로 얻어진 동역학계가 원래 동역학계와 많이 달라질 수 없음을 보였습니다. 이에 대해 조금 더 자세히 이야기해 봅시다.
정규화
서로 다른 두 대상의 한 성질을 비교하기 위해 다른 성질들을 동일하게 맞추어 주는 과정을 정규화라고 합니다. 지구와 축구공의 모양을 비교해 본다고 가정해 봅시다. 우리는 지구와 축구공을 동시에 한눈에 담을 수 없음에도 두 모양이 같다고 쉽게 대답할 수 있습니다. 아마 지구의 사진이나 지구본을 떠올리며 축구공과의 모양을 비교했을 것입니다. ‘모양’이라는 것은 크기와는 독립적인 성질이기 때문에 우리 마음대로 크기를 축소 또는 확대해서 비교할 수 있는 것이죠. 모양의 비교를 편하게 하기 위해 물체들을 비슷한 크기로 확대 또는 축소하는 과정을 정규화로 생각할 수 있습니다.
동역학계의 재정규화
다시 일반적인 동역학계 \(f:X\to X\)를 생각해봅시다. \(Y\)를 \(X\)의 한 부분집합이라고 합시다. 만약 \(n\)초 후에 \(Y\)의 모든 점이 다시 \(Y\)로 돌아온다면, 정의역과 공역을 모두 \(Y\)로 제한한 새로운 동역학계 \(f^{\circ n}|_Y:Y\to Y\) 를 얻습니다. 수학적으로 엄밀하게는 동역학계의 공형동치류conformal equivalence classes of dynamical systems를 생각하기 때문에 별도의 확대/축소의 과정 없이 \(f^{\circ n}|_Y\) 자체를 \(f\)의 재정규화로 정의합니다. 하지만 앞서 설명한 정규화의 개념과의 연결을 위해, 우리는 \(Y\)에서 정의된 동역학계 \(f^{\circ n}|_Y:Y\to Y\)를 \(X\)와 비슷한 크기를 가지도록 적당히 확대한 동역학계를 \(f\)의 \(Y\)에서의 재정규화로 생각합시다. 다시 말해 동역학계의 재정규화는 전체공간 \(X\) 의 작은 부분공간 \(Y\)에 유도되는 동역학계를 \(X\)와 비슷한 크기로 확대(정규화)한 동역학계를 의미합니다.
재정규화의 선험적 유계a priori bound와 MLC 추측
다시 복소동역학에서 가장 유명한 망델브로집합의 국소적 연결성을 보이는 문제MLC 추측를 생각해 봅시다. 요코즈Yoccoz에 의해 \(f_c\)가 유한번만 재정규화가 가능한 \(c\)에서는 망델브로집합이 국소적으로 연결되어있음이 증명됐습니다. \(f_c\)가 재정규화가 무한 번 가능한 경우 류비취Lyubich에 의해 재정규화의 선험적 유계와 망델브로집합의 \(c\)에서 국소적 연결됨이 관련되어 있음이 보여졌습니다. 그래서 무한 번 재정규화가 가능한 다항식에 대한 재정규화의 선험적 유계를 보이는 것이 중요한 문제로 자리 잡게 되었습니다.
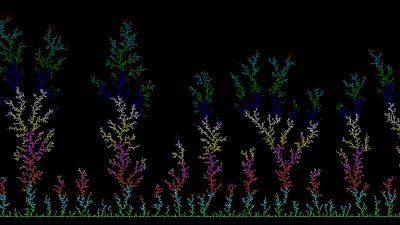
재정규화의 선험적 유계는 무엇을 의미할까요? 재정규화는 작은 부분에 유도되는 동역학계를 확대해서 얻은 새로운 동역학계로 생각할 수 있었습니다. 재정규화가 선험적으로 유계라는 것은, 이렇게 확대해서 얻은 동역학계들이 확대하기 전의 동역학계로부터 크게 달라질 수 없음을 의미합니다. 조금 더 정확히 말하자면 작은 부분의 동역학계를 확대할 때 가로-세로를 다른 비율로 확대해야 원래 동역학계를 얻을 수 있는데, 이 가로-세로 비율이 많이 다르지 않음을 의미합니다.
[그림3]을 봅시다. 바실리카\(^2\)(\(\approx z^2-1.3107\))는 바실리카로 한 번 재정규화가 가능합니다. 그래서 작은 바실리카 줄리아집합을 포함하고 있는 것이죠. 바실리카\(^3\)(\(\approx z^2-1.38155\))은 두 번 재정규화가 가능하고, 한 번의 재정규화로 얻은 동역학계는 바실리카\(^2\)입니다. 그 증거로 바실리카\(^2\)의 줄리아집합을 포함하고 있음을 볼 수 있습니다. 이 과정을 계속하여 바실리카\(^\infty\)(\(\approx z^2-1.401155)\)를 얻을 수 있습니다. 바실리카\(^\infty\)의 재정규화는 자기 자신이 되므로 재정규화를 계속 반복할 수 있습니다. 즉 무한히 작은 자기 자신을 포함하고 있는 것이죠. 이 무한 번 재정규화가 가능한 다항식은 파이겐바움Feigenbaum 다항식이라고도 불립니다.
설리반은 \(c\)가 실수일 때 \(f_c\)의 재정규화가 선험적 유계임을 보이는 문제의 해결에 큰 공헌을 했습니다.
3.떠돌지 않는 영역 정리
앞서 예시에서 보았듯 복소유리함수 \(f\)의 반복합성으로 정의되는 동역학계는 리만구 \(\hat{\mathbb{C}}\)를 줄리아집합과 파투집합이라 불리는 두 집합으로 분해합니다. 이번에는 각각의 점들이 어떻게 움직이는지가 아닌 파투집합의 연결성분connected component들이 \(f\)에 의해서 어떻게 움직이는지를 생각해봅시다.
바실리카 줄리아집합[그림2-a]을 봅시다. 검은 원판들과 바깥의 흰 영역이 모두 파투연결성분들입니다. 모든 검은 원판들은 \(f\)의 반복에 의해 결국 0,-1 을 포함하는 주기가 2인 두 개의 검은 주기적 원판들로 보내집니다. 바깥 흰색 영역은 \(f\)에 의해 자기 자신으로 대응되므로 주기가 1인 주기적 파투연결성분입니다. 즉, 모든 파투연결성분들은 \(f\)의 반복에 의해 주기적인 파투연결성분으로 보내짐을 관찰할 수 있습니다.
설리반은 임의의 복소유리함수에 대해 파투연결성분들이 주기적인 파투연결성분으로 보내짐을 보였습니다. 이를 떠돌지 않는 영역 정리라고 부릅니다.
떠돌지 않는 영역 정리가 중요한 이유는 파투집합에서의 동역학을 잘 이해할 수 있게 해주기 때문입니다. 주기적인 파투 연결집합에서의 동역학은 (1) 주기적인 점들에 의해 끌어당겨지거나 (2) 무리수 각도로 회전하거나 둘 중 하나라는 것이 슈바르츠 보조정리를 통해 어렵지 않게 증명됩니다. 즉, 우리는 주기적인 파투 연결집합에서의 동역학을 이해하고 있고, 떠돌지 않는 영역 정리는 모든 파투 연결성분이 시간이 지나면 결국 주기적인 파투 연결성분으로 대응됨을 말해줍니다.
4.일반적인 동역학계
수학적 성질들이 모든 경우에는 성립하지 않지만, 일반적인generic 경우에는 성립할 때가 많습니다. 일반적임을 정의하기 위해 상황에 따라 다양한 개념들이 이용됩니다. (예: 열린 조밀한 집합, 측도가 0인 집합의 여집합 등) 동역학자들은 일반적인 동역학계가 다음의 성질을 만족하는지에 관심이 있습니다.
⋅(구조적 안정성) 어떤 동역학계를 살짝 변형해도 원래 동역학계와 (주로 미분-위상적으로) 동일하다면, 우리는 이 동역학계를 구조적으로 안정되었다고 합니다.
⋅ (쌍곡성) 국소적으로 항상 팽창하는 방향과 수축하는 방향으로 나눌 수 있으면 이를 쌍곡적인 동역학계라고 합니다.
동역학계를 약간 변화시키더라도 팽창, 수축하는 성질은 그 크기만 달라질 뿐 대체로 유지됩니다. 그래서 많은 경우 동역학계가 쌍곡적이면 구조적으로 안정되는 경우가 많고, 복소동역학에서도 쌍곡적인 복소유리함수들은 구조적으로 안정되어 있음을 어렵지 않게 보일 수 있습니다. 설리반은 마녜Mañé, 사드Sad와의 공동연구에서 구조적으로 안정된 복소유리함수들의 집합이 전체 복소유리함수들의 공간에서 열린 조밀한 집합임을 보였습니다. 즉, 구조적 안정성이 일반적인 성질임을 보였습니다. 이와 관련한 다음의 질문들이 중요한 추측으로 남아있습니다.
(1) (쌍곡성의 조밀성) 쌍곡적인 복소유리함수들의 집합은 전체 복소유리함수 공간에서 조밀한가?
(2) (구조적 안정성 \(\Rightarrow\) 쌍곡성) 구조적으로 안정된 복소유리함수들은 쌍곡적인가?
마녜-사드-설리반의 결과에 의해 (2)는 (1)을 함의합니다. 한편 설리반은 클라이니안군에 대해서는 구조적 안정성이 쌍곡성을 함의한다는 것을 보였습니다.
5.설리반의 사전
클라이니안군은 PSL(2,\(\mathbb{C}\)) 의 이산부분군discrete subgroup입니다. PSL(2,\(\mathbb{C}\))는 3차원 쌍곡공간 \(\mathbb{H}^3\)의 등거리 사상들의 군이기 때문에, 클라이니안군은 쌍곡기하학적 구조가 주어진 3차원 다양체로도 생각을 할 수 있습니다.
설리반은 복소동역학과 클라이니안군론 모두에서 중요한 연구를 했을 뿐 아니라 그사이의 유사성을 다양한 관점으로 입증했습니다. 예를 들어 앞서 언급한 떠돌지 않는 영역 정리는 알포스Ahlfors의 클라이니안군의 유한성 정리와 대응이 됩니다. 실제로 설리반은 떠돌지 않는 영역 정리를 증명하며 같은 방법을 이용해 클라이니안군의 유한성 정리의 새로운 증명을 제시했습니다. 두 분야 사이의 유사성은 이를 체계적으로 정리한 설리반의 이름을 따서 설리반의 사전이라고 불립니다. 아래 표는 설리반의 사전 중 몇 개의 예시를 나열한 것입니다.
| 복소동역학 | 클라이니안군론 |
|
줄리아집합 파투집합 주기적 순환 블레쉬케 곱 설리반의 떠돌지않음 정리 써스톤의 특성화 정리 쌍대성의 조밀성 추측 MLC 추측 |
극한집합 비연속성 영역 닫힌 측지선 푹쉬안 군 알포스의 유한성 정리 써스톤의 기하화 정리 기하적 유한성의 조밀성 정리 엔딩 레미네이션 정리 |
설리반의 사전이 잘 맞는 부분도 있지만 때로는 유사성이 깨지는 경우도 있기 때문에, 두 분야 간의 비교를 통해 기존에 생각지 못한 흥미로운 질문들을 얻는 경우가 많습니다.
맺음말
설리반의 업적에 대해 조사하고 글을 정리하며 감명받은 점은 다양한 분야에서 고루 중요한 연구 결과를 지금까지도 계속해서 내고 있다는 점이었습니다. 설리반의 개인 홈페이지를 보면 140개가 넘는 논문들을 20개의 다른 분야들로 분류한 것을 볼 수 있습니다. 새로운 분야를 끊임없이 배우는 호기심과 열정, 다양한 분야를 아우르는 통찰력, 새로운 이론과 관점을 제시하는 독창성 등 설리반은 존경받을 면을 두루 갖춘 수학자라는 생각이 들었습니다. 설리반의 아벨상 수상을 다시 한 번 진심으로 축하드리고, 후대 수학자들이 나아갈 길을 제시하고 좋은 본보기를 보여 주심에 감사드리며 이 글을 마칩니다.