대수다양체의 방정식의 관계식 [1]: 대수다양체를 정의하는 방정식

이 연재 ‘대수다양체의 방정식의 관계식’에서는 대수기하학의 중요한 연구 주제 중 하나인 대수다양체의 기하학적 성질과 대수다양체를 정의하는 방정식의 대수적 성질 사이의 관계에 대해 2편의 글을 통해 소개하려고 한다. 수학을 전공하지 않은 일반 독자들에겐 유클리드 기하학은 친숙하겠지만 대수기하학이나 복소기하학과 같은 현대의 기하학 분야들은 다소 생소할 것이다. 오늘날 수학자들은 유클리드 기하학을 유클리드 공간 \(\mathbf{R}^n\) 안에서 일어나는 기하학적 현상을 탐구하는 분야로 여긴다. 중고등학교 때 \(n=2\) 또는 \(3\)인 경우를 다룬다. \(\mathbf{R}^2\)에서 원과 직선이 어떻게 만나는지, \(\mathbf{R}^3\)에서 구와 평면이 어떻게 만나는지 등에 대해 배웠을 텐데, 이런 것이 유클리드 기하학의 기본적인 내용이다. 19세기에 수학자들은 유클리드 기하학 이외에도 다양한 기하학이 존재한다는 것을 깨달았고, 이후 200여 년의 시간 동안 다양한 기하학 분야의 발전이 이어졌다. 이번 글에서는 현대의 수학자들이 연구하는 기하학 분야 중 복소기하학과 대수기하학에 대해 간략히 소개한 뒤 대수기하학의 주요 연구 대상인 대수다양체를 정의하는 방정식이 무엇인지 설명하도록 하겠다.

   먼저 복소기하학과 대수기하학과 같은 새로운 종류의 기하학이 왜 필요한지 간단한 예를 통해 알아보자. 유클리드 평면 \(\mathbf{R}^2\)는 좌표 \((x,y)\)를 가지는데, \(x,y\)를 변수로 갖는 다항식 \(f(x,y)\)에 대하여,

\(Z(f):=\{(x,y) \in \mathbf{R}^2 \mid f(x,y)=0\}\)

와 같이 정의되는 도형을 생각할 수 있다. 많은 기본적인 도형들이 이와 같이 표현될

수 있다. 예를 들어 \(Z(x^2+y^2-1)\)은 원, \(Z(y-x^2)\)은 포물선, \(Z(x^2-y^2-1)\)은 쌍곡선이다.[그림1] 다항식 \(f(x,y)\)가 2차식일 때, \(Z(f)\)가 퇴화^degenerate된 경우가 아니라면,¹ 이차곡선 \(Z(f)\)는 타원, 포물선, 쌍곡선 중 하나가 된다는 것은 잘 알려져 있다.

다항식 \(f(x,y)\)가 3차식일 때, 삼차곡선 \(Z(f)\)의 기하학적 형태가 몇가지 나오는지를 묻는 것은 자연스러운 질문이다. 17세기 말 뉴턴^{Isaac Newton}은 72개의 기하학적 형태가 있다는 것을 발견하였고, 이후 6개의 추가적인 형태가 더 발견되었다. 3차식인 경우만 해도 경우가 너무 많고 복잡하다. 하지만 복소기하학과 대수기하학에서는 \(Z(f)\)의 기하학적 형태는 \(f\)의 차수에 의해서만 결정된다.

   복소기하학에서는 \(x,y\)가 복소수 값을 가지는 것을 허용한다. 즉, \(x,y\)를 변수로 갖는 다항식 \(f(x,y)\)에 대하여,

\(Z(f):=\{(x,y) \in \mathbf{C}^2 \mid f(x,y)=0\}\)

와 같이 정의되는 도형을 생각한다. 복소수를 사용할 때 장점 중 하나는

\(f(x,y) \neq 0\)이라면 \(Z(f)\)는 항상 공집합이 아닌 도형이 된다는 것이다.² 예를 들어 \(Z(x^2+y^2+1)\)은 \(\mathbf{R}^2\)에서는 공집합이지만 \(\mathbf{C}^2\)에서는 공집합이 아니다. 실수 위에서 생각하면 \(\mathbf{C}^2\)는 4차원이고 \(Z(f)\)는 2차원이 되지만, 복소기하학에서는 \(\mathbf{C}^2\)는 2차원이고 \(Z(f)\)는 1차원 ‘곡선’이라 여긴다. 유클리드 기하학에서처럼 \(f(x,y)\)가 1차 다항식일 때 \(Z(f)\)는 \(\mathbf{C}\)와 같은 ‘직선’이 된다. 서로 다른 두 직선은 한 점에서 만나거나 평행하다. 하지만 \(\mathbf{C}^2\)를 콤팩트화하여 복소사영평면 \(\mathbf{P}^2\)로 만들면 서로 다른 두 직선은 항상 한 점에서 만난다. 현대의 많은 기하학에서는 공간을 콤팩트화하여 다루는데, 많은 강력한 이론들이 콤팩트 공간에만 적용되기 때문이다.

   일반적으로 복소사영공간 \(\mathbf{P}^r\)은 \(\mathbf{C}^r\)을 콤팩트화하여 얻어진다. 사영공간 \(\mathbf{P}^r\)은 동차좌표^{homogeneous coordinate} \([x_0, x_1, \ldots, x_r]\)를 가진다. 동차좌표에서는 0이 아닌 복소수 \(\lambda\)에 대해 \([x_0, x_1, \ldots, x_r]=[\lambda x_0, \lambda x_1, \ldots, \lambda x_r]\)이 된다. 이제 \(x_0, x_1, \ldots, x_r\)을 변수로 가지는 유한개의 동차다항식 \(f_1, f_2, \ldots, f_k\)에 대하여

\(Z(f_1, f_2, \ldots, f_k):=\{x \in \mathbf{P}^r \mid f_1(x)=f_2(x)=\cdots =f_k(x)=0\}\)

를 생각할 수 있다. 대수적으로 정의된 기하학적 대상인 \(Z(f_1, f_2, \ldots, f_k)\)를 ‘대수다양체’라고 부르며, 대수기하학의 주된 연구 대상이다. 힐버트의 영점정리에 따르면 \(Z(f_1, f_2, \ldots, f_k) \neq \emptyset\)인 것은 \(g_1f_1 + g_2f_2 + \cdots + g_k f_k = 1\)이 되는 다항식 \(g_1, g_2, \ldots, g_k\)가 존재하지 않는 것과 동치이다. 이제 \(x_0, x_1, x_2\)를 변수로 갖는 다항식 \(f(x_0, x_1, x_2)\)에 대하여 \(\mathbf{P}^2\)에 있는 ‘평면곡선’ \(Z(f)\)를 생각할 수 있다. 만약 \(f\)의 차수가 \(d\)이고 \(Z(f)\)가 퇴화되지 않았다면, \(Z(f)\)는 종수^genus가

\(g=\frac{(d-1)(d-2)}{2}\)

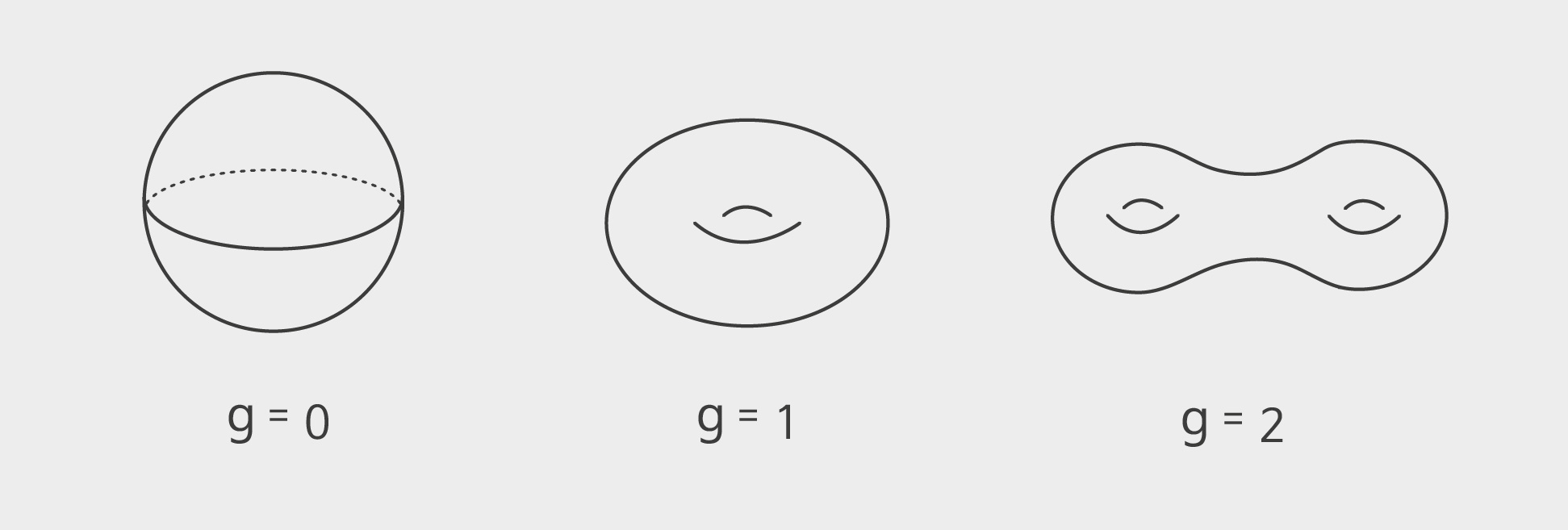
인 콤팩트 리만 곡면^{compact Riemann surface}이 된다. 종수가 \(g\)인 콤팩트 리만 곡면의 기하학적 형태는 구에 구멍이 \(g\)개 있는 모양이다. 예를 들어, \(d=1\) 또는 \(2\)이면 \(Z(f)\)의 기하학적 모양은 구와 같고, \(d=3\)이면 \(Z(f)\)의 기하학적 모양은 도넛과 같다.[그림2] 유클리드 기하학에서 평면곡선의 기하학적 형태를 분류하는 것은 거의 불가능한 일이지만, 복소기하학과 대수기하학적인 관점을 도입하면 이렇게 문제가 매우 쉽고 간결하게 해결이 된다. 뿐만 아니라 복소기하학과 대수기하학에서는 차수가 각각 \(d\)와 \(e\)인 두 평면곡선 \(Z(f)\)와 \(Z(g)\)는 중복도를 고려하면 항상 \(de\)개의 점에서 만난다는 베주 정리^{Bezout Theorem}도 성립한다. 이를 이용해 평면곡선에 대한 많은 기하학적 문제들이 매우 쉽고 간결하게 해결될 수 있다. 유클리드 기하학에서 원과 직선 또는 원과 원의 관계는 경우가 많고 복잡하지만, 복소기하학과 대수기하학에서는 이차곡선과 일차곡선은 항상 두 점에서 만나고, 이차곡선과 이차곡선은 항상 네 점에서 만난다. 즉, 새로운 기하학은 새로운 관점에서 문제를 해석하여 매우 강력한 결과를 이끌어 낼 수 있다고 결론을 내릴 수 있다.

   복소기하학의 주된 연구 대상은 복소다양체이다. 복소다양체는 복소공간 \(\mathbf{C}^n\)의 부분들을 이어 붙여서 만들어지는데, 이 복소다양체의 차원을 \(n\)이라 한다. 앞서 언급한 구에 몇 개의 구멍이 있는 리만 곡면은 1차원 복소다양체의 대표적인 예이다. 복소차원 1은 실수차원 2에 해당하기 때문에 리만 ‘곡면’을 복소 ‘곡선’으로 간주한다. 복소다양체는 기하학적 형태만 고려하지 않고 그 위에 있는 ‘복소 구조’ 또한 고려한다. 복소 구조는 복소해석학에서 다루는 정칙 함수^{holomorphic function}에 의해 주어진다. 정칙 함수란 복소해석학적으로 계속해서 미분을 해도 다시 정칙 함수가 되는 매우 특별한 함수이다. 여기서는 복소다양체는 매우 풍부한 수학적 구조를 가지고 있다고 이해를 하고 넘어가면 된다.

   앞에서 살펴본 것처럼 만약 복소다양체가 사영공간에 매립되어 있고 다항식의 해집합으로 표현이 된다면, 이 복소다양체는 대수기하학에서 다루는 대수다양체가 된다. 이제 복소다양체의 기하학적 성질과 다항식의 대수학적 성질을 연관시키는 것을 생각해볼 수 있다. 복소다양체의 기하학적 성질은 많은 경우 복소해석학의 문제로 환원을 시킬 수 있다. 다항식의 대수학적 성질은 가환대수학의 연구 주제이다. 복소다양체를 사영공간에 매립시키는 것은 대수기하학을 통해 매우 상이한 분야인 기하학, 해석학, 대수학을 연결하는 의미가 있는 문제이다. 예를 들어 대수학의 문제인 함수체^{function field} \(f(x,y,z)\)의 일반적인 3차 확장체^{extension field}가 \(f(x,y,z)\)와 같은가를 생각해보자. 이는 100년 정도 사람들이 해결하지 못한 문제였다. 대수기하학을 이용하면 이 문제는 일반적인 3차 3차원 다양체^{cubic threefold}가 유리적^rational인가를 묻는 기하학적 문제와 동치라는 것을 알 수 있다. 이 문제는 1972년 클레멘스^{Herbert Clemens}와 그리피스^{Phillip Griffiths}에 의해 복소해석학적 방법론이 핵심에 놓여있는 핫지 이론^{Hodge Theory}을 통해 해결되었다.

   실제로 어떤 복소다양체가 사영공간 \(\mathbf{P}^r\)에 매립^embedding 가능한지를 묻는 것은 20세기 초중반 수학계의 중요한 문제였다. 차우^{Wei-Liang Chow}의 정리에 따르면 사영공간에 매립된 복소다양체는 항상 다항방정식의 해집합으로 표현되기 때문에, 복소다양체가 사영공간에 매립되는 것은 대수다양체가 되는 것과 동치이다. 고다이라^{Kunihiko Kodaira}는 복소다양체가 양적인 선다발^{positive line bundle}을 갖는 것이 사영공간에 매립되는 것과 동치라는 것을 증명하여 1954년 필즈상을 수상하였다.

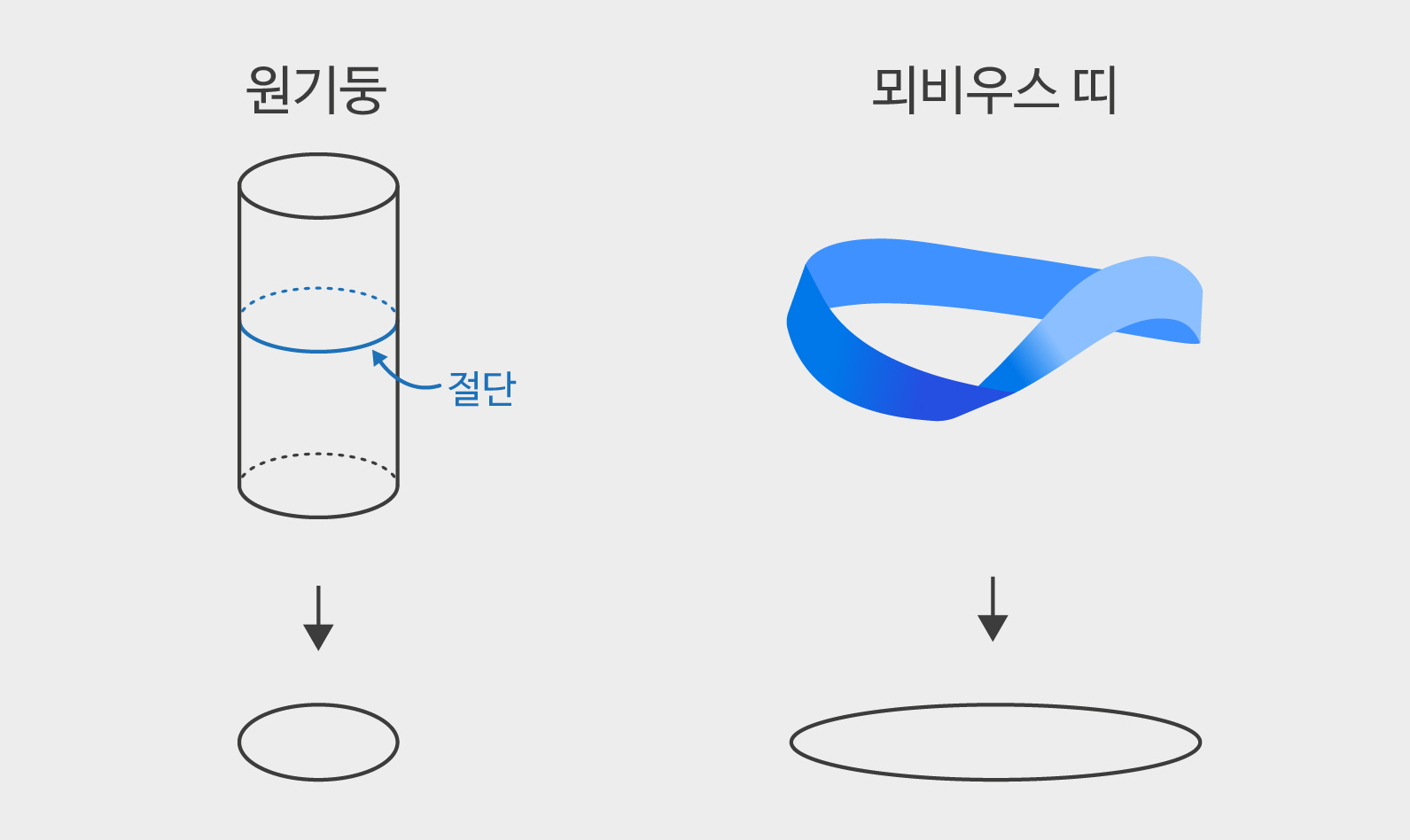
   선다발은 복소다양체의 각 점마다 복소직선 \(\mathbf{C}\)가 달려있는 공간이다. 원기둥과 뫼비우스 띠는 모두 원의 각 점마다 선분이 달려있는 공간인데, 모든 선분을 직선으로 연장하면 원 위의 선다발이 된다.[그림3] 물론 이것은 실수 세계에서의 선다발의 예이다. 복소곡선 위의 선다발은 실수 차원으로는 4차원이라 복소다양체의 선다발의 형태를 상상해보는 것은 매우 어려운 일이다. 복소다양체 \(X\)를 고정하고 두개의 선다발을 텐서곱^{tensor product} 해주면 또 다른 선다발이 된다. 선다발 두 개를 어떻게든 ‘더해서’ 새로운 선다발을 만들어낼 수 있다고 받아들이고 넘어가자. 선다발이 주어지면 절단^section을 생각할 수 있는데, 이는 주어진 복소다양체에서 선다발로 가는 매립사상으로 간주할 수 있다.³

원기둥을 연장하여 원 위의 선다발로 본다면, 수 없이 많은 원이 쌓여있다고 볼 수 있는데, 이 원들이 절단의 예이다. ‘양적’인 선다발의 정의는 매우 기술적이다. 선다발의 곡률미분형식^{curvature form}을 정의할 수 있는데, 선다발이 ‘양적’이란 것은 곡률미분형식으로부터 파생되는 행렬이 ‘양의’ 정부호^{positive definite}란 뜻이다. 두 개의 양적인 선다발을 더해준 것은 다시 양적인 선다발이 되는데, 이는 보다 더 양적인 선다발이 된다고 여길 수 있다. 주어진 양적인 선다발 \(L\)을 매우 많이 더해주면 매우 양적인 선다발이 된다고 볼 수 있다. 실제로 대수기하학에서 매우 풍부한 선다발^{very ample line bundle}이라 부르는 것이 된다. 여기서 ‘매우 풍부한’이란 수학적으로 엄밀하게 정의된 용어인데, 선다발의 절단이 매우 풍부하게 많고 이를 이용하여 복소다양체를 사영공간에 매립시킬 수 있기 때문에 붙여진 이름이다.

   복소다양체 \(X\)가 매우 풍부한 선다발 \(L\)에 의해 사영공간 \(\mathbf{P}^r\)에 매립되어 있다고 하자.⁴ 사영공간 \(\mathbf{P}^r\)의 동차좌표를 \([x_0, x_1, \ldots, x_r]\)라 놓자. 앞서 언급한 차우 정리는 \(x_0, x_1, \ldots, x_r\)을 변수로가지는 유한개의 동차다항식

\(f_1, f_2, \ldots, f_k\)가 존재하여 \(X=Z(f_1, f_2, \ldots, f_k)\) 이 된다는 내용이다. 즉 복소다양체 \(X\)는 다항방정식 \(f_1= f_2=\cdots= f_k=0\)으로 정의되는 대수다양체이다.⁵ 대수기하학의 가장 근본적인 연구 주제 중 하나는 대수다양체 \(X\)와 선다발 \(L\)의 기하학적 성질과 대수다양체 \(X\)를 정의하는 다항식 \(f_1, f_2, \ldots, f_k\)의 대수적 성질 사이의 관계를 탐구하는 것이다. 이와 관련된 대수기하학의 중요한 문제를 하나 소개하겠다. 선다발 \(L\)이 매우 풍부하지만 절단이 풍부하지 않은 경우가 있다. 예를 들어 \(n\)차원 대수다양체 \(X\)을 \(\mathbf{P}^{n+2}\)로 매립시키는 선다발이 있을 수가 있다. 물론 이러한 \(X\)는 \(n \geq 3\)이면 기본군^{fundamental group}이 자명하고 피카드군^{Picard group}이 순환군^{cyclic group}이 되는 등 기하학적으로 매우 특수해야한다. 1970년대 핫숀^{Robin Hartshorne}은 \(n \geq 5\)일 때 이러한 대수다양체 \(X\)를 정의하는 다항식은 단 2개뿐일 것이라고 예상을 하였는데,⁶ 아직도 해결되지 못하고 있다. 놀랍게도 이 문제는 \(\mathbf{P}^{n+2}\)의 계수^rank가 2인 벡터다발이 모두 자명한 것밖에 없다는 것과 동치인 문제이다. 대수다양체 위의 벡터다발을 모두 분류하는 것은 대수기하학의 매우 중요한 문제로 사영공간의 계수가 2인 벡터다발을 분류하는 것은 그 중에 가장 기본적인 문제라 할 수 있다. 핫숀의 추측은 대수기하학의 가장 기본적인 문제가 매우 어려운 이유를 대수다양체의 방정식에 대한 어려운 문제와 연결시켜 설명해주고 있다.

   필즈상 수상자인 멈포드^{David Mumford}는 1960년대 말 선다발 \(L\)이 ‘충분히’ 양적인 경우 대수다양체 \(X\)를 정의하는 다항식의 차수가 모두 2가 된다는 것을 증명하였다.[1] 선다발이 충분히 양적이라는 것은 고정된 선다발에 충분히 많은 양적인 선다발을 더해주었다고 이해하면 된다. 멈포드의 정리로부터 임의의 대수다양체 \(X\)가 항상 2차 동차다항식으로 정의될 수 있다는 것을 말해준다. 2차 동차다항식은 2차 형식^{quadratic form}으로 이해할 수 있기 때문에 수학에서 가장 강력한 도구 중 하나인 선형대수학을 이용하여 대수다양체를 연구할 수 있는 가능성을 열어주었다. 스미스^{Gregory G. Smith}와 시드만^{Jessica Sidman}은 대수다양체를 정의하는 2차 다항식이 모두 1차 다항식을 성분으로 가지는 어떤 행렬 한 개의 소행렬식^minor이라는 것을 증명하였다. 이는 대수다양체를 정의하는 2차 형식의 계수가 4 이하라는 것을 말해준다. 다른 한편으로 멈포드의 정리는 선다발의 충분히 양적인 성질(기하학적 성질)로부터 대수다양체를 정의하는 다항식의 차수가 2라는 성질(대수적 성질)을 이끌어내고 있다. 여기서 자연스러운 질문은 선다발이 얼마나 양적이어야 대수다양체를 정의하는 다항식의 차수가 2가 되는지를 묻는 것이다. 이 질문은 대수다양체의 차원이 1인 대수곡선의 경우 해결 되었지만 대수다양체의 차원이 2 이상인 경우는 부분적으로만 해결 되어 있다.

   지금까지 우리는 대수다양체를 정의하는 방정식이 어떻게 주어지는지 선다발의 양적인 성질과 관련지어 간략히 살펴보았다. 다음 연재글에선 대수곡선의 경우 선다발의 양적인 성질을 어떻게 측정하고 이것이 대수곡선을 정의하는 다항식의 성질과 어떤 관계가 있는지에 대해 다룰 것이다. 그리고 대수곡선의 결과가 고차원 대수다양체의 경우로 어떻게 확장이 되는지 설명하며 연재를 마칠 계획이다.