모델론 맛보기 [1]: 한정기호 제거

수리논리학에는 크게 4가지 분야가 있습니다: 계산가능성이론^{computability theory}, 모델론^{model theory}, 증명론^{proof theory}, 그리고 집합론^{set theory}.¹ 이 중 저의 연구 분야인 모델론에 대해서 간단히 소개하려고 합니다. 모델론은 무엇을 연구할까요? 창^{C. C. Chang}과 키슬러^{H. J. Keisler}는 모델론을 다음과 같이 표현하였습니다.[1]

“Model theory is the branch of mathematical logic which deals with the relation between a formal language and its interpretations, or models.“

즉, 특정 논리식(혹은 논리식들의 모임)을 만족하는 구조들,

즉 주어진 논리식(들)을 만족하는 모델들을 연구하거나 혹은 반대로 특정 모델(혹은 모델들의 모임)이 만족하는 논리식들을 연구합니다.

특히 본 글에서는 한정기호 제거^{quantifier elimination}라는 모델론의 개념을 알아보고, 이를 통해 모델론이 타 수학분야에 어떻게 응용이 되는지 살펴보도록 하겠습니다.

1. 한정기호 제거

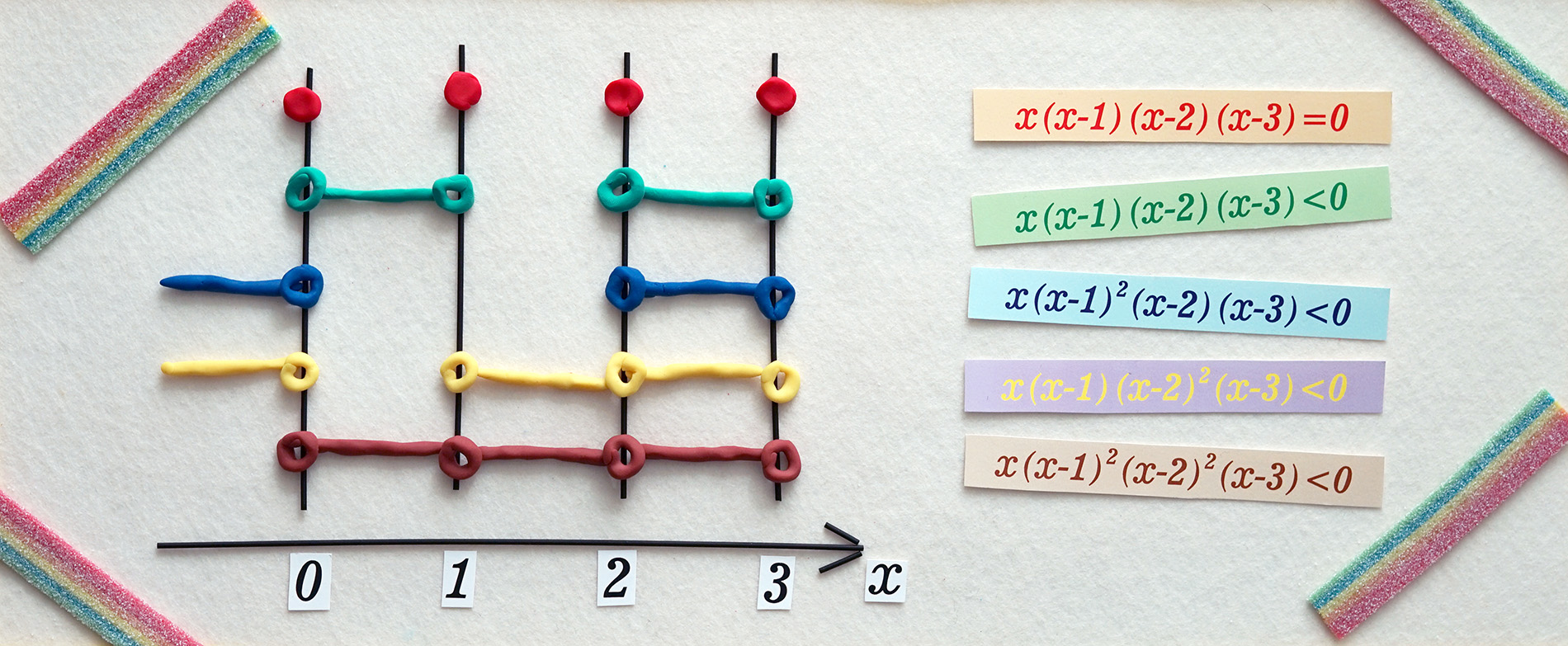
구체적으로 실수 순서체 \(\mathbb{R}\)를 통해서 `한정기호 제거’ 개념이 무엇인지 알아보도록 하겠습니다. 실수 순서체에는 덧셈 `\(+\)’, 뺄셈 `\(-\)’, 곱셈 `\(\times\)’이 있고, 이 연산들과 잘 부합하는 순서관계 `\(<\)’가 있어, 다항함수에 대한 방정식뿐만 아니라 부등식을 생각할 수 있습니다. 이 방정식과 부등식의 해집합을 정의가능한 원자집합^{definable atomic set}이라고 명명하겠습니다. 예를 들어, 실수들의 유한집합 \(\{a_1,\ldots,a_n\}\)은 방정식 \((x-a_1)\cdots (x-a_n)=0\)의 해집합으로 표현되기 때문에 정의가능한 원자집합이 됩니다. 혹은 열린 구간 \((-\infty,a)\), \((a,\infty)\), \((a,b)\)들은 부등식 \(x<a\), \(-x<-a\), 혹은 \((x-a)(x-b)<0\)의 해집합이 되기 때문에, 정의가능한 원자집합이 됩니다. 일반적으로 실직선 상의 정의가능한 원자집합은 정확하게 유한개 점들의 모임이거나 혹은 유한개의 열린 구간의 합집합으로 표현되는 집합들입니다. 예를 들어, 두 열린 구간의 합집합 \((0,1)\cup (1,2)\)은 부등식 \(x(x-1)^2(x-2)<0\)의 해집합이 됩니다. 또한, 실평면상의 반지름이 \(r\)이고 중심이 \((a,b)\)인 열린 원판은 부등식 \((x-a)^2+(y-b)^2<r^2\)의 해집합으로 표현되기 때문에 정의가능한 원자집합이 됩니다.

그리고 이 정의가능한 원자집합들의 부울 연산, 즉 교집합, 합집합, 그리고 여집합을 생각할 수 있습니다. 뿐만 아니라 사영함수

\(\pi_n:\mathbb{R}^{n+1}\rightarrow \mathbb{R}^n,(x_1,\ldots,x_n,x_{n+1})\mapsto (x_1,\ldots,x_n)\)

에 대한 상을 생각할 수 있습니다. 이런 집합들을 정의가능한 집합^{definable set}이라고 명명하겠습니다. 즉, 정의가능한 집합들의 모임은 정의가능한 원자집합들을 포함하고, 부울 연산 및 사영함수 \(\pi_n\)의 상을 취하는 것에 대해서 닫혀있는 가장 작은 모임이 됩니다. 예를 들어, 실평면 상의 반지름이 \(1\)이고 원점을 중심으로 갖는 열린 원판의 반쪽, \(\{(x,y):x^2+y^2<1,\ y>0\}\)은 정의가능하지만 원자집합은 아닙니다. 그리고 실직선상의 정수들의 모임 \(\{\ldots, -1,0,1,\ldots\}\)은 정의가능하지 않습니다.

그렇다면 구체적으로 어떤 집합들이 정의가능 할까요? 사칙연산 및 순서관계에 의해서, 부등식의 해들은 정의가능한 집합이 될 것입니다. 또한, 이 해집합의 부울 연산을 취해서 생성되는 집합들 또한 정의가능합니다. 즉, 연립부등식의 유한 합집합들은 정의가능하게 됩니다. 그런데 사영함수의 상을 취하는 과정에 의해서 이런 집합 뿐만 아니라 다른 형태의 집합도 정의가능한 집합이 될 수 있을 것 입니다. 하지만 1951년 타르스키^{A. Tarski}는 정의가능한 집합은 연립부등식의 해들과 이 집합들의 부울 연산에 의해서 생성되는 집합이 전부라는 것을 증명하였습니다.[3] 따라서, 정의가능한 집합은 연립부등식의 해집합의 유한 합집합으로 표현됩니다.

뿐만 아니라 연립부등식의 해집합들의 모임에 대해 사영함수의 취했을때 상들이 유한개의 연립부등식에 의해서 결정된다는 사실을 증명하였습니다. 변수 \(x\), \(\bar y=(y_1,\ldots,y_k)\), \(\bar z=(z_1,\ldots, z_l)\)에 대한 정수계수 다항함수 \(p_1,\ldots, p_n,q_1,\ldots,q_m\in \mathbb{Z}[x,\bar y,\bar z]\)에 대해서, \(V\subseteq \mathbb R^{1+|\bar y|+|\bar z|}\)를 연립부등식

\(\begin{cases}p_1>0,\ldots, p_n>0\\q_1=\ldots=q_m=0\end{cases}\)

의 해집이라합시다. 또한, 사영함수

\(\pi_{x\bar y \bar z,\bar z}:\mathbb R\times \mathbb R^{|\bar y|}\times \mathbb R^{|\bar z|}\rightarrow \mathbb R^{|\bar z|},(a,\bar b,\bar c)\mapsto \bar c\)

를 통한, \(V\)의 파이버들의 모임을 \(\mathcal F\)라고 합시다. 즉,

\(\begin{align*}\mathcal F&=\{V_{\bar c}=V\cap \pi_{x\bar y\bar z,\bar z}^{-1}(\bar c):\bar c\in \mathbb R^{|\bar z|}\}\\&=\{V\cap \left(\mathbb R\times \mathbb R^{|\bar y|}\times \{\bar c\}\right):\bar c\in \mathbb R^{|\bar z|}\}\end{align*}\)

가 됩니다. 그러면 사영함수

\(\pi_{x\bar y,\bar y}:\mathbb R\times \mathbb R^{\bar y}\rightarrow \mathbb R^{|\bar y|},(a,\bar b)\mapsto \bar b\)

에 대한 파이버들의 상은 유한개의 연립부등식에 의해서 결정이 됩니다. 즉, 어떤 자연수 \(N\)이 존재하여, 자연수 \(i\le N\)에 대해서, 다항함수 \(P_{i,1},\ldots, P_{i,s},\ldots, Q_{i,1},\ldots,Q_{i,t}\in \mathbb Z[\bar y,\bar z]\)가 존재하여 다음이 성립합니다: 임의 실수 순서쌍 \(\bar c\in \mathbb R^{|\bar z|}\)에 대해서, 어떤 \(k(=k(\bar c))\le N\)가 존재하여, 연립부등식

\(\begin{cases}P_{k,1}(\bar y,\bar c)>0,\ldots,P_{k,s}(\bar y,\bar c)>0,\\Q_{k,1}(\bar y,\bar c)=\ldots=Q_{k,t}(\bar y,\bar c)=0.\end{cases}\)

의 해집합이 정확히 \(V_{\bar c}\)의 사영함수 \(\pi_{x\bar y,\bar y}\)에 대한 상을 묘사합니다. 이런 사실을 `한정기호 제거’라고 불립니다.

이 사실을 1계 논리^{first order logic}의 논리식^formula으로 표현하면 다소 생소하게 들리는 ‘한정기호 제거’라는 이름이 보다 명확해집니다. 논리식을 소개하기에 앞서, 논리식을 표현할 1계 논리의 언어^language를 소개하겠습니다. 1계 논리의 언어 \(\mathcal L\)는 다음과 같은 기호들로 이루어져 있습니다.

(1) 논리기호
     • (연결기호) \(\neg\), \(\wedge\), \(\vee\), \(\rightarrow\)
     • (등호) \(=\)
     • (한정기호) \(\exists\), \(\forall\)
     • (변수) \(x,y,z,\ldots\)
     • (보조기호) \((,)\)

(2) 특정기호
     • (술어기호) 자연수 \(n\ge 1\)에 대해, \(n\)-항 술어기호
     • (함수기호) 자연수 \(n\ge 1\)에 대해, \(n\)-항 함수기호
     • (상수기호) 상수기호

특히 1계 논리의 언어 \(\mathcal L\)는 특정기호에 의해서 결정되기 때문에 보통 논리기호들은 생략하고 특정기호들의 모임을 \(\mathcal L\)로 표기합니다. 예를 들어, 군^group을 표현하기 위해 1차 논리의 언어 \(\mathcal L_g=\{\cdot, \Box^{-1},1\}\)을 사용합니다:

     • (함수기호) 군의 연산을 표현하는 이항 함수기호 \(\cdot\),
                       역원 표현하는 일항 함수기호 \(\Box^{-1}\).
     • (상수기호) 항등원을 표현하는 상수기호 \(1\).

환^ring을 표현하기 위해서는 1차 논리의 언어 \(\mathcal L_r=\{+,-,\times,0,1\}\)을 사용합니다:

     • (함수기호) 덧셈 및 곱셈을 표현하는 이항 함수기호 \(+,\times\),
                       덧셈에 대한 역원을 나타내는 일항 함수기호 \(-\).
     • (상수기호) 덧셈 및 곱셈의 항등원을 표현하는 상수기호 \(0,1\).

또한, 순서체를 표현하기위해 1차 논리의 언어 \(\mathcal L_{or}=\mathcal L_r\cup \{<\}\)을 사용합니다:

     • (술어기호) 순서관계를 나타내는 이항 술어기호 \(<\).
     • (함수기호) 덧셈 및 곱셈을 표현하는 이항 함수기호 \(+\),\(\times\),
                       덧셈에 대한 역원을 나타내는 일항 함수기호 `\(-\)’.
     • (상수기호) 덧셈 및 곱셈의 항등원을 표현하는 상수기호 \(0,1\).

주어진 1계 논리의 언어 \(\mathcal L\)에 대한 논리식^formula이란, \(\mathcal L\)에 들어가는 기호들의 적절한 나열입니다. 예를 들어, 1계 논리의 언어 \(\mathcal L_{or}\)에 대해서 다음의 기호들의 나열은

\(\varphi\equiv \forall x \forall y\left((x<y)\rightarrow \exists z (y+(-x)=z^2)\right)\)

논리식이 됩니다. 특히 논리식 \(\varphi\)은 `임의 원소 \(x\)와 \(y\)에 대해서 \(x\)가 \(y\)보다 작다면, \(y-x\)가 제곱수로 표현이 된다’라는 것을 표현합니다. 물론 이 논리식이 모든 순서체에 대해서 성립하지는 않습니다. 예를 들어, 유리수체의 경우 이 논리식이 참이 되지 않습니다. \(x=0\), \(y=2\)에 대해서, \(y-x=2>0\)임에도 불구하고 \(2\)는 유리수의 제곱으로 표현되지 않습니다. 하지만 이 논리식은 실수체에서는 참이 됩니다.

다음의 기호들의 나열 또한 논리식이 됩니다:

\(\psi\equiv (x<y)\rightarrow \exists z (y-x=z^2)\)

그런데 이 논리식에 있는 변수 \(x\)와 \(y\)는 특정하게 한정되어 있지 않아 자유변수^{free variable}라고 부릅니다. 보통 자유변수 \(x\)와 \(y\)의 존재를 강조하고자 \(\psi(x,y)\)로 표기합니다. 자유변수가 있는 논리식들에 대해서는 참 혹은 거짓을 판별하는 것이 말이 되지 않습니다. 하지만 주어진 순서체에 대해서 자유변수 \(x\)와 \(y\)에 특정 원소들을 대입하였을 때, 참 혹은 거짓을 판별할 수 있습니다. 예를 들어, \(\psi(0,2)\equiv 0<2\rightarrow \exists z(2-0=z^2)\)는 유리수체에 대해서는 거짓이 되고 실수체에 대해서는 참이 됩니다.

이제 실수체에 대한 `한정기호 제거’ 결과가 논리식으로 어떻게 표현되는지 살펴보겠습니다. 다음의 논리식이 실수 순서체 \(\mathbb R\)에서 참이 됩니다: 연립부등식

\begin{align*}\varphi(x,\bar y, \bar z)&\equiv \bigwedge_{i\le n} p_i(x,\bar y,\bar z)>0\wedge \bigwedge_{j\le m} g_j(x,\bar y,\bar z)=0,\\\psi_k(\bar y,\bar z)&\equiv \bigwedge_{i\le s}P_{k,i}(\bar y,\bar z)>0\wedge\bigwedge_{j\le t}Q_{k,j}(\bar y,\bar z)=0,\end{align*}

에 대해서,

\(\forall \bar z\left(\forall y\left (\exists x\left(\varphi(x,\bar y,\bar z)\right)\leftrightarrow \bigvee_{k\le N} \psi_k(\bar y,\bar z)\right)\right).\)

여기서 주목할 점은 한정기호 `\(\exists x\)’를 포함하는 논리식 \(\exists x(\varphi(x,\bar y,\bar z))\)이 한정기호 `\(\exists x\)’ 및 변수 `\(x\)’이 없는 논리식 \(\bigvee_{k\le N} \psi_k(\bar y,\bar z)\)와 동치가 된다는 사실입니다.

또한, 이 `한정기호 제거’는 실수체 뿐만 아니라 임의 닫힌 실체^{real closed field}에 대해서도 성립합니다. 닫힌 실체는 임의 홀수 차수의 일변수 다항함수가 항상 해를 갖는 순서체를 의미합니다. 예를 들어, 실수체는 닫힌 실체가 되고, 또한 대수적 실수들로 이루어진 체, 즉 유리계수 다항식의 해가 되는 실수들의 모임 또한 닫힌 실체가 됩니다. 하지만 유리수체는 닫힌 실체가 되지 않습니다. 예를 들어, 유리계수 다항함수 \(x^3-2\)는 유리수 해를 갖지 않습니다.

2. `한정기호 제거’의 응용

모델론에서 중요한 연구대상 중의 하나는 다양한 수학적 구조들에 대해 정의가능한 집합들을 이해하는 것입니다. 이때 `한정기호 제거’는 적절히 정의가능한 원자집합들을 선택함으로서 정의가능한 집합들을 구체적으로 이해하는데 매우 큰 도움이 됩니다. 이런 정의가능한 집합들의 이해는 모델론의 응용에 있어 중요한 역할을 합니다.

복소수체 \(\mathbb C\)의 경우, 정의가능한 집합들이 정확히 건설가능한 집합^{constructible set}, 즉 다항함수에 대한 연립방정식의 해집들의 부울 조합^{boolean combination}으로 나오게 됩니다. 이로부터 ‘건설가능한 집합의 다항함수에 대한 상은 다시 건설가능한 집합이 된다’는 체발리^{C. Chevalley} 정리의 모델론을 사용한 증명을 얻게 됩니다.[4]

본 글에서 다루었던 실수체 \(\mathbb R\)의 경우, 정의가능한 집합들이 정확히

준대수 집합^{semialgebraic set}, 즉 다항함수에 대한 연립방정식의 해집합의 유한 합집합이 된다는 것을 알 수 있습니다. 이를 활용하여 힐버트의 17번째 문제에 대한 증명을 얻을 수 있습니다.² 그리고 `한정기호 제거’를 통해 \(\mathbb R^1\)의 정의가능한 부분집합은 항상 점과 열린 구간의 유한 합집합으로 표현된다는 것을 관찰할 수 있는데, 이런 성질을 갖는 순서 구조들을 o-minimal 하다고 부릅니다. o-minimality는 필레이^{A. Pillay}와 스테인호른^{C. Steinhorn}에 의해서 처음 정의되었으며[5] o-minimality에 대한 연구는 실대수기하^{real algebraic geometry}와 매우 밀접한 관계가 있습니다.³ 또한, o-minimality 이론의 발전은 최근 앙드레-우트 추측^{André-Oort conjecture}를 증명하는데 있어서 매우 핵심적인 역할을 하였습니다.[7][8]

또한, p진체 \(\mathbb Q_p\)에 대해서도 정의가능한 원자집합들을 적절히 선택하여 `한정기호 제거’를 얻을 수 있습니다. 부치체 구조로부터 가장 자연스러운 정의가능한 원자집합의 형태는 p진수 계수를 갖는 다항함수 \(p,q\)에 대해 부치부등식 \(\nu(p)\ge \nu(q)\)의 해집합 혹은 방정식 \(p=0\)의 해집합을 생각할 수 있습니다. 그런데 이런 형태의 원자집합들은 `한정기호 제거’ 결과를 얻기에 충분하지 않습니다. 예를 들어, 사상함수 \(\pi:\mathbb Q_p^2\rightarrow \mathbb Q_p,(x,y)\mapsto x\)에 대한, 집합 \(V=\{(x,y):x=y^2\}\)의 상은 절대로 다항함수에 대한 연립부치부등식 및 연립방정식의 해집합들의 부울 조합으로 나오지 않습니다.[9] 하지만 매킨타이어^{A. Macintyre}는 p진수 계수를 갖는 \(n\)-변수 다항함수 \(p\)와 자연수 \(m\ge 1\)에 대해서 방정식의 \(p(\bar x)=y^m\)의 해집합의 사상함수 \(\pi_n:\mathbb Q_p^n\times \mathbb Q_p\rightarrow \mathbb Q_p^n,(\bar x,y)\mapsto y\)의 상을 정의가능한 원자집합으로 추가하면 `한정기호 제거’가 성립함을 보였습니다.[9] 데넵<sup>J. Denef</sup>은 이 p진체에 대한 `한정기호 제거’ 결과를 사용하여 p진 정수 \(\mathbb Z_p\) 계수를 갖는 다항함수들로 이루어진 연립방정식에 대해, p 거듭제곱 환 \(\mathbb Z/p^n\mathbb Z\) 해들의 갯수에 대한 생성함수로 주어지는 푸앵카레 급수가 유리함수가 된다는 것을 증명하였습니다.[10]