들어가며 : 편집자의 말
인간은 범주화를 통해 이 복잡한 세상을 인식하고 헤쳐 나간다. 먹을 수 있는 것과 먹어서는 안 되는 것을 구분하는 것처럼 생존에 직결된 문제부터 음악을 트로트, 록, 발라드, R&B 등으로 분류하는 취향의 문제에 이르기까지 모든 것을 범주화하면 대부분의 문제를 보다 쉽게 풀 수 있다. 생각해보라. 음악 스트리밍 서비스를 이용하는데, 장르, 음악가, 시기, 앨범 등과 같은 분류가 전혀 없이 세상에 존재하는 모든 음악을 하나의 거대한 리스트로 만들어둔다면 이 얼마나 비효율적이겠는가?
인간의 지적 행위인 학문 역시 예외가 아니어서 한국연구재단은 학술연구지원사업 효율화를 위해 학문분야를 인문학, 사회과학, 자연과학, 공학, 의약학, 농수해양학, 예술체육학의 7개 대분류로 나누어 놓고 있다. 이 중에서 자연과학 분야 안에는 우리가 중고등학교 때부터 배워서—비록 그 내용은 친숙하지 않을지라도 분류만큼은—친숙한 수학, 물리, 화학, 생물 등이 포함되어 있다. 많은 경우에 이렇듯 학문 분야를 분류할 수 있는 것은 각 분야가 갖는 대표적인 특징이 있기 때문이다. 이를테면 수학은 숫자나 행렬, 변수, 도형 등 다양한 수학적 개체들 사이의 관계를 탐구하는 학문, 물리는 원자나 그보다 작은 입자들부터 우주 전체에 이르기까지 자연에 존재하는 규칙을 찾는 학문, 화학은 주로 원자 단위에서 결합과 분리를 통해 물질을 이해하는 학문, 생물학은 자연에 존재하는 다양한 물질과 물체 중 생명체를 탐구하는 학문 등으로 이해하는 식이다. 이렇게 분류할 때 아주 약간의 교집합은 존재할 수 있겠지만, 대부분의 학문 분야는 서로 다른 대상을 탐구하기 때문에 각각 독립적으로 존재할 수 있을 것처럼 느껴진다. 그렇지만 의외로 출발점과 목적지가 다른 것 같은 학문 분야들이 공통의 관심사로 수렴하여 마주치기도 한다. 물론 공통의 관심사라고 하더라도 주제에 접근하고 이해하는 방식, 주제에 대해 궁극적으로 해결하고자 하는 문제가 같은 것은 아니다. 그래서 어쩌면 서로 다른 학문 분야 내에서 비슷한 연구 주제에 대해 어떤 관점에서 관심을 갖는지 살펴보는 것은 더더욱 흥미로운 일일지 모르겠다.
그래서 호라이즌에서는 앞으로 하나의 주제를 서로 다른 학문 분야에서 어떻게 다루는지 다양한 예를 살펴보고자 한다. 첫 번째 주제로 1982년 발견된 ‘준결정’에 대해 살펴볼 것이다. 앞서 언급한 바와 같이 인간은 세상에 존재하는 물질들 역시 범주화하였는데, 크게는 고체, 액체, 기체로 분류하고, 그중 고체는 금속과 같은 결정질 물질이나 유리와 같은 비결정질 물질로만 분류하면 된다고 믿었다. 그런데 1982년 비결정이라고 하기에는 원자 배열에 규칙이 있지만 결정이라고 부르기에는 그 규칙이 불충분한 물질이 발견된 것이다. 이 새로운 물질의 발견은 ‘화학’ 분야의 공로로 인정되었고, 그 결과 준결정을 발견한 단 세흐트만은 2011년에 노벨 화학상을 받았지만, 이 물질을 제대로 이해하는 데에는 화학뿐만 아니라 물리학과 수학 역시 크게 기여를 하고 있다. 이런 이유로 준결정이라는 하나의 탐구 대상을 놓고 앞으로 ‘준결정의 화학’, ‘준결정의 물리학’ 그리고 ‘준결정의 수학’, 이렇게 세 편의 글을 소개하고자 한다. 이 글들이 독자들에게도 세상을 다양한 각도에서 살펴보는 즐거움을 줄 수 있기를 기대해 본다.
2011년 단 셰흐트만Dan Shechtman 교수는 준결정을 처음 발견한 공로로 노벨 화학상을 수상했다. 기존에 결정은 공간적인 주기성을 가지는 물질로 규정되었지만, 1982년 준결정 발견 후에 개념이 확장되어 회절 패턴이 잘 보이면 결정으로 정의되었다. 즉 준결정의 발견은 결정의 정의를 바꾼 획기적인 사건이었다.
필자는 2011년 노벨상 발표를 듣고 크게 놀랐다. 특히 화학상이 준결정 분야로 갔다는 부분에 흥분을 감출 수 없었다. 2002년부터 미국 로렌스버클리 국립연구소에서 준결정 관련된 연구를 했었기 때문에 그 학계의 분위기도 잘 알고 있었다. 2005년에 미국 아이오와주 AMES 연구소에서 개최된 국제준결정 학회International Conference on Quasicrystal에 참석했을 때 단 셰흐트만 교수님이 준결정의 역학적 마찰력 특성에 많은 관심이 있으셨고 관련해서 많은 대화를 했던 기억이 있다. 지금은 고인이 된 준결정 표면연구의 거장인 아이오와주립대 화학과 팻 틸Pat Thiel교수님과 준결정의 마찰력 그리고 준결정 표면이 얼마나 아름다운가에 대한 많은 대화와 논의를 했었다. 필자는 올해 11월 미국진공학회American Vacuum Society에서 준결정 위의 마찰력에 대한 초청강연을 하였고 매우 오래간만에 발표하는 주제라서 당시에 많은 기억들을 다시 생각하였다. 이러한 기억을 모아 준결정의 개념 및 표면, 그리고 다양한 응용에 대해서 논하고자 한다.
준결정의 구조
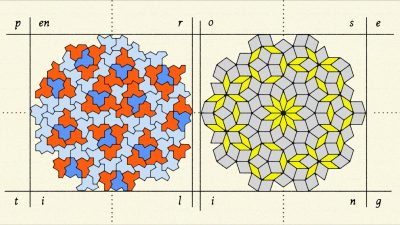
준결정은 공간적인 주기성을 가지지 않는다. 그 대신 회전대칭성rotational symmetry을 가진 물질이다. [그림2]처럼 5각형이나 10각형은 기존의 결정이론에서는 존재할 수 없지만 준결정은 그러한 구조를 보여준다.
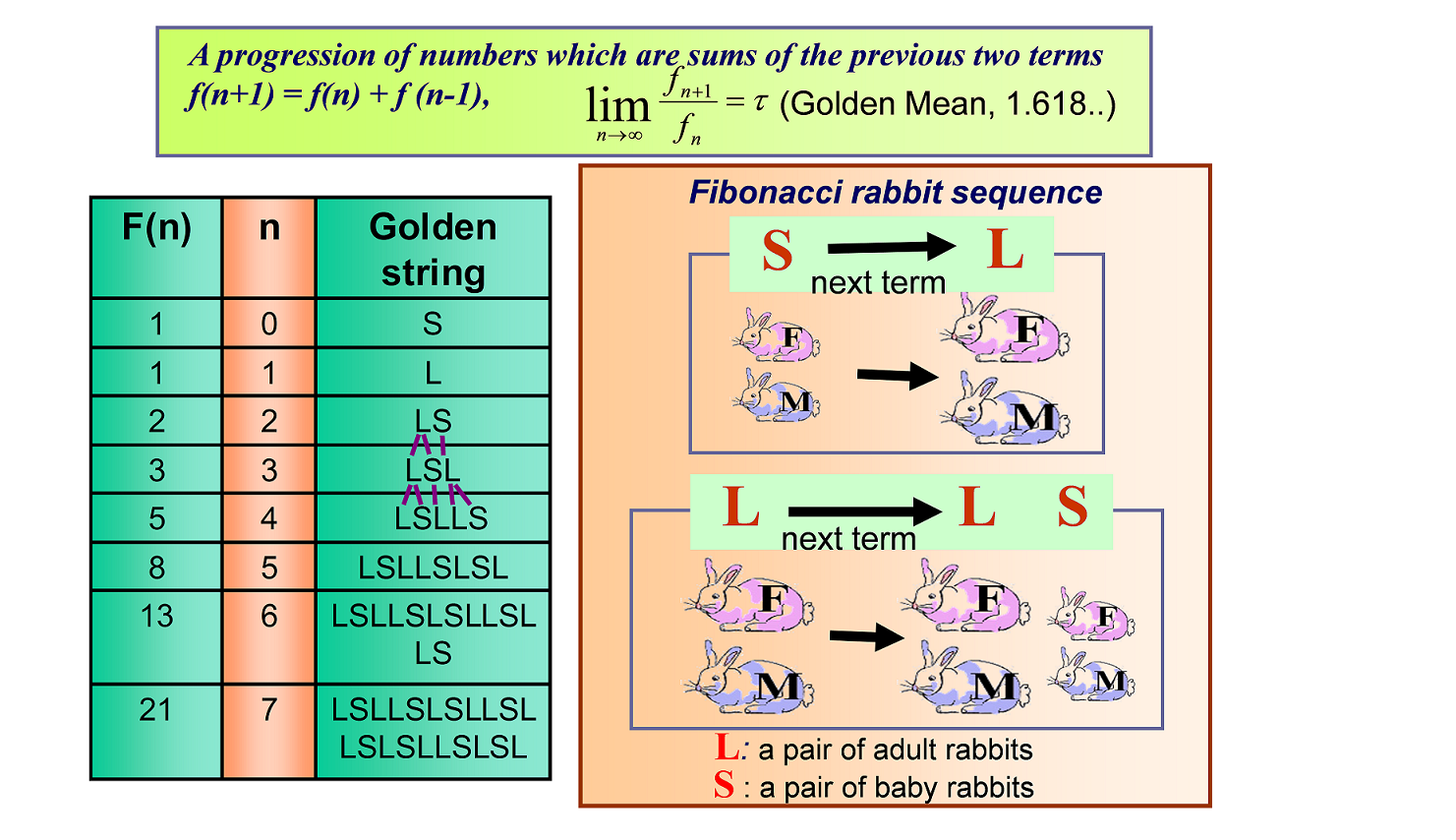
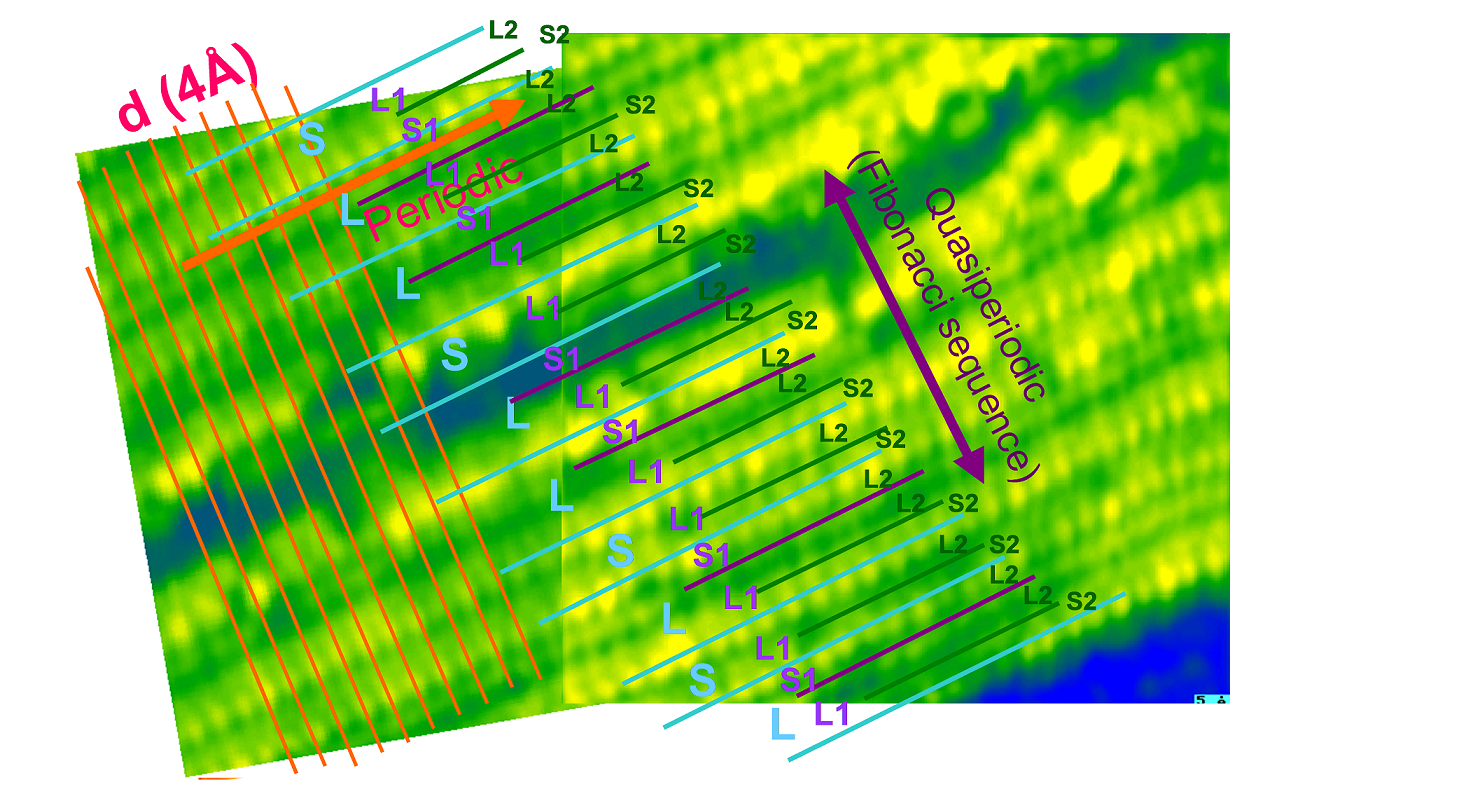
또한 준결정은 그 유명한 피보나치 수열과 황금비율을 따르는 물질이다. [그림2]의 오른쪽 전자투과현미경 이미지는 이러한 피보나치 수열구조의 피보나치 문자열 (LSLLSLSLLSLLS.. )과 피보나치수열 (0-1-1-2-3-5-8-13-21-34-… )의 패턴을 따르게 된다. 그리고 피보나치 수 역시 황금비율(=1.1618…)을 따르게 된다. 즉 피보나치 수열에서 바로 인접한 앞 위 두 수의 비를 계산해 보면 수가 커지면 커질 수로 황금비율로 근접하는 것을 알 수 있다.
피보나치 문자열에 대해서 이해하기 위해서는 피보나치 토끼순서에서 먼저 시작해야 한다. 즉 새끼 토끼 암수쌍 S가 다음 달에 성체 토끼 암수쌍 L이 되고 성체 토끼 암수쌍 L은 다음 달에 성체 및 새끼 토끼 암수쌍 LS로 진화하는 패턴이다. 따라서 시작이 S이면 다음 달에 L, 그다음 달에 LS, 그다음 달에는 LSL, 그리고 LSLLS, LSLLSLSL 등으로 진화한다. 이러한 피보나치 문자열의 문자의 수는 피보나치 수와 일치한다.([그림3]) 이러한 진화의 패턴은 나중에 보여줄 준결정의 원자의 배열에 그대로 나타나게 된다.
준결정의 표면 및 응용성
흥미롭게도 준결정은 매우 낮은 표면에너지를 가진다.[1] 예를 들면 Al-Pd-Mn 준결정의 표면에너지는 25 mJ/m2로 다른 금속보다 매우 낮고 테플론과 비슷한 수준이다. 이러한 낮은 표면에너지는 준결정의 표면이 벌크와 유사한 구조를 가지게 만든다. 즉 표면에너지가 크면 표면은 재구조화를 하는데 표면에너지가 낮기 때문에 준결정은 표면이 벌크와 같은 구조bulk-terminated를 가진다. 또한 준결정의 마찰력은 매우 낮다. 이를테면 Al-Cu-Fe 준결정의 마찰계수는 0.05-0.2로 철(0.32) 혹은 구리(0.42)보다 매우 낮다.[2] 이러한 준결정의 낮은 표면에너지와 낮은 마찰력 그리고 높은 강도hardness는 준결정의 다양한 응용을 가능하게 한다. 낮은 표면에너지는 잘 달라붇지 않는 코팅이 가능하고 이러한 점을 이용하여 후라이팬이나 전기면도기의 코팅으로 준결정이 쓰였다.([그림4])
준결정의 마찰력연구
이렇게 다양한 응용성을 가진 준결정의 낮은 마찰력은 많은 궁금증을 야기했다. 가장 핵심적인 질문은 낮은 마찰력이 준결정의 구조, 즉 준주기성aperiodicity과 근본적인 연관성을 가지는가였다. 필자는 이런 질문을 가지고 2002년 로렌스버클리연구소에서 연구를 시작하였다. 하지만 마찰력은 매우 복잡한 특성이고 공기 중에 준결정은 산화막으로 금방 뒤덮여 연구를 위해 초고진공이 필요했다. 또한 마찰력 연구를 위해 마찰력현미경이 필요했고, 원자구조를 보기 위해 주사터널링현미경 기법을 이용했다.
마찰력과 준주기성/주기성의 상관관계를 보기 위해서 선택한 시료는 10각형의 Al-Ni-Co 준결정 시료였고, 이 시료는 흥미롭게도 한 축은 주기성을 가지고 다른 2개의 축은 준주기성을 보여준다. 따라서 적절한 평면을 고르게 되면 (여기서는 2-대칭(2f) 표면) 한 평면에 주기성과 준주기성을 둘 다 가지는 독특한 표면을 얻게된다.([그림5])
이러한 표면의 원자구조는 주사터널링현미경으로 확인할 수 있었고 여기서 완벽한 피보나치 수열의 진화 패턴을 보여주는 준주기성을 가지는 원자의 배열을 볼 수 있고 다른 축의 방향은 주기성의 원자배열을 볼 수 있다.([그림6]) 마찰력현미경을 이용한 결과 주기적으로 배열된 원자들은 훨씬 더 큰 마찰력을 보여준다는 점을 관찰할 수 있었고 이는 준결정의 낮은 마찰력이 준주기성과 근본적으로 연관된다는 점을 보여준다.[3]
이러한 결론은 실제 마찰력이 작용하는 산화막으로 덮인 준결정 코팅 그리고 공기 중에서는 어떠한 의미일까? 다양한 실험결과는 산화막이 덮이면 이러한 마찰력과 준기성과의 관계를 보기가 힘들다는 점을 보여준다. 왜냐하면 결정구조가 없는 산화막이 주기성이나 준주기성을 가지는 원자배열을 보기가 힘들게 하기 때문이다. 하지만 산화막을 투과하는 순간 주기성을 가지는 표면은 준주기성을 가지는 표면보다 높은 마찰력을 보여주게된다. 즉 산화막을 관통하는 순간 주기성 혹은 준주기성을 가지는 원자들과 접촉을 하게되고 마찰력은 변하게 된다.
준결정의 피보나치 수열을 따르는 원자적인 구조는 물질이 아름다울 수 있다는 점을 보여주고 흥미롭게도 다양한 응용성을 지닌다. 이러한 점에서 준결정은 지적인 아름다음intellectual beauty와 실용적인 응용practical application과의 만남이다. 준결정에 대한 응용은 우수한 역학적 특성에 기반한 코팅에 그치지 않고 화학촉매, 수소 흡착 등의 다양한 방향으로 확대되고 있다. 앞으로 다양한 준결정에 대한 다학제적인 연구와 새로운 응용성을 기대해본다.
참고문헌
- C. J. Jenks and P. A. Thiel, Langmuir 1998, 14 1392-1397.
- Useful Quasicrystal, J. M. Dubois (World Scientific, 2005).
- J. Y. Park et al. Science 309, 1354 (2005).
- J. Y. Park, and P. A. Thiel, Journal of Physics: Condensed Matter 20, 314012 (2008).