Upward, not Northward.
– Edwin A. Abbott, <Flatland: A Romance of Many Dimensions>
플랫랜드Flatland라는 세계가 있다. 플랫랜드는 나와 내 동족들이 사는 세계이다. 사실 플랫랜드는 우리가 아는 유일한 세계이기 때문에 엄밀하게 따로 정해진 이름이 없다. 적어도 내가 얼마 전에 우리의 세계보다 더 높은 차원이 있다는 것을 알기 전까지는 그랬다. 이제부터 우리의 세계와 이 글을 읽고 있는 독자들의 세계를 구분하기 위해서 편의상 우리의 세계를 플랫랜드라고 부르도록 하자. 플랫랜드라는 이름이 암시하듯이 우리가 살고 있는 세계는 독자들이 보기에 2차원 평면이다.
나의 이름은 “A 스퀘어Square”이다. 앞서 말했듯이 나는 플랫랜드에 살고 있다. 따라서 내 몸도 2차원 평면에 국한되어 있다. 스퀘어라는 이름이 암시하듯이 나는 독자들이 보기에 사각형이다. 플랫랜드에는 나와 같은 사각형 말고도 다양한 다각형들이 살고 있다. 플랫랜드에서 사회 생활을 하는 데에 있어서 자기 자신과 상대방이 얼마나 많은 변을 가지고 있는지를 아는 것은 굉장히 중요하다. 왜냐하면 플랫랜드에서 사회적 지위는 변의 개수에 따라서 결정되기 때문이다.
사각형과 오각형은 학자, 법률가, 의사 등과 같은 전문직 상류층을 형성하고, 육각형과 그보다 변의 개수가 많은 다각형들은 귀족과 성직자 계급을 형성한다. 특히, 플랫랜드는 아직도 절대 왕정 체제인데, 왕은 변의 개수가 무수히 많은 다각형으로 거의 원으로 보인다. 왕이 원에 가까운 다각형이어야 한다는 전통은 아마도 원이 가장 완벽한 도형이라는 믿음에서 나왔을 것이다. 이러한 사회 체제 아래에서 그나마 다행인 것은 자식은 부모보다 변의 개수가 한 개씩 늘어난다는 사실이다. 세대를 거듭할수록 적어도 자손은 현재 자기 자신보다 높은 사회적 지위를 누리는 것이 보장되는 것이다.
예외는 이등변 삼각형isosceles triangle이다. 이등변 삼각형의 자식은 변의 개수가 늘어나지 않는다. 대신 한 세대가 지날 때마다 예리한 모서리의 각도가 0.5도씩 증가한다. 이등변 삼각형의 사회적 지위는 병사나 노동자로 제한되어 있다. 만약에 이등변 삼각형의 자식이 모두 사각형이 될 수 있다면 사회에 필요한 노동력에 큰 문제가 생길 것이다. 여기서도 그나마 다행인 것은 이등변 삼각형의 자손은 세대를 거듭할수록 정삼각형equilateral triangle에 가까워진다는 사실이다. 정삼각형은 장인 및 기술자 계급을 형성한다.
그리고 가장 중요하게 정삼각형의 자식은 사각형이 될 수 있다. 나의 아버지도 정삼각형이었다. 아버지는 내가 태어났을 때 무척 좋아하셨다. 아니, 내가 태어나는 것을 평생 기다리셨다.
자, 이제 독자들은 플랫랜드에서 다각형의 변의 개수가 얼마나 중요한지 이해했을 것이다. 그런데 아이러니하게도 이렇게 중요한 변의 개수를 파악하는 것은 플랫랜드의 구조적인 성질에 의해서 그리 쉽지 않다. 기억하라. 우리는 2차원 평면에 갇혀 있다. 우리에게 우리 자신은 모두 선분line segment으로 보인다!
그렇다면 우리는 어떻게 상대방의 변의 개수를 파악할 수 있을까? 크게 보아 3가지 기술이 있다. 청각 기술Art of Hearing, 촉각 기술Art of Feeling, 그리고 시각 인지 기술Art of Sight Recognition이 바로 그것들이다.
우선, 청각 기술은 다른 모양의 다각형들이 서로 다른 목소리를 가진다는 사실에 기반한다. 하지만 불행히도 이 기술에는 매우 중대한 문제점이 하나 있다. 바로 변의 개수가 적은 다각형들이 자신들의 목소리가 실제보다 변의 개수가 많은 것처럼 들리도록 변형시키는 기만 전술을 개발했다는 것이다.
다음 기술은 촉각 기술이다. 촉각 기술은 변의 개수를 확실하게 잴 수는 있지만 품위가 없다고 여겨진다. 처음 만나는 상대방을 다짜고짜 더듬는 일은 확실히 예의 바른 방식이라고 말할 수는 없을 것이다.
마지막으로, 시각 인지 기술이 있다. 품위 있는 방식이라고 여겨지지만 많은 연습이 필요하고 특정한 조건이 만족되어야 한다는 제약이 있다. 특정한 조건은 바로 “안개”가 끼어 있어야 한다는 것이다. 도대체 뜬금없이 안개는 왜 필요한 것일까?
앞서 말했듯이 우리가 보기에 우리 자신은 모두 선분이다. 공기가 아주 깨끗해서 무한히 먼 곳까지 선명하게 볼 수 있다면, 선분 중간에 존재하는 두 변이 만나는 부분, 즉 모서리는 전혀 눈에 띄지 않을 것이다. 하지만 안개가 끼어 있다면 상황이 다르다. 모서리를 중심으로 해서 그 모서리에 맞닿아 있는 두 변은 뒤로 가면서 상대적으로 흐려질 것이다. 이러한 상황에서 많은 연습을 한다면 모서리 주변으로 두 변이 상대적으로 흐려지는 정도를 정밀하게 파악하여 모서리의 각도를 추정할 수 있다.
참고로 플랫랜드에서 삼각형 이상의 다각형들은 모든 변의 길이가 정확하게 같은 정다각형이어야만 한다. 비정형 다각형들은 기형으로 취급되어 사회에서 격리된다. (심지어 이러한 비정형 다각형들은 결국 아주 잔인하게 처형된다는 소문도 있다.) 이것이 의미하는 바는 사회에서 일반적으로 만나게 되는 다각형의 경우에 모서리의 각도를 알면 상대방이 어떤 다각형인지 판단할 수 있다는 것이다!
시각 인지라는 개념이 나왔으니까 하는 말인데, 플랫랜드의 학자들은 아직 정확하게 빛이 무엇인지 알지 못한다. 우선 빛이 전혀 없을 때 아무것도 볼 수 없기 때문에 빛이 시각과 밀접한 관계가 있다는 사실은 자명하다. 하지만 이러한 빛이 도대체 어디에서 오는지는 파악하지 못하고 있다. 특히 모든 방향이 벽으로 꽉 막힌 밀폐된 방도 왜 낮이 되면 밝아지는지 아무도 모른다.
성직자들이 말하듯이 빛은 정말 무에서 유로 창조되는 것일까?
이 문제는 플랫랜드의 지식인들 사이에서 큰 수수께끼이다. 하지만 이제 내게 이 문제는 더 이상 수수께끼가 아니다. 다만, 불행히도 현재 나는 이 문제를 풀어서 얻은 기쁨을 즐기기에는 너무 심각한 공황 상태에 빠져 있다. 플랫랜드보다 더 높은 차원의 세계가 있다는 것을 알아버렸기 때문이다.
세 번째 밀레니엄이 시작되던 첫날, 나는 느지막하게 일어나서 하루를 시작하고 있었다. 그러던 중 이상한 느낌이 들어서 주위를 둘러보았다. 그 순간 아무도 없던 방 안에 갑자기 매우 작은 선분이 나타나는 것이 아닌가? 유령인가?
본능적으로 나는 갑자기 나타난 선분이 무슨 다각형인지 파악하려고 애썼다. 하지만 불행히도 방 안에는 안개가 충분히 끼어 있지 않아서 모서리의 각도를 추정하는 것이 쉽지 않았다. 하지만 예리한 각도가 아닌 것만은 분명했다. 귀족 유령인가?
그렇게 나타난 선분은 길이가 점점 길어졌다. 나에게 다가오는 것인가?
그런데 선분의 길이 변화가 신원 미상인 다각형이 나에게 가까이 다가오기 때문이라기에는 방 안이 너무 좁았다.
“당신, 누… 누구야?” 나는 무서웠지만 묻지 않을 수 없었다.
“내 이름은 스피어Sphere라고 한다.” 선분이 말했다. 생전 처음 들어보는 종류의 목소리였다. 목소리로는 무슨 다각형인지 전혀 알 수 없었다.
나는 두려움을 최대한 숨기며 물었다. “스피어라고? 그런데 당신은 무슨 다각형이요?”
“나는 다각형이 아니고, ‘구’라는 입체 도형이다.”
“입체? 입체가 뭐죠?”
“다각형이 2차원에 존재하는 도형이라면, 입체는 3차원에 존재하는 도형이지.”
나는 속으로 생각했다. ‘뭐지? 3차원?!’
내가 황당한 표정으로 아무 말도 하지 않자 자신을 “스피어”라고 부르는 선분은 다음과 같이 말을 이어갔다.
“나는 2차원보다 더 높은 차원, 즉 3차원이 있다는 것을 알려주기 위해서 천 년에 한번씩 너희의 세계, 즉 플랫랜드를 방문하고 있다. 플랫랜드에 사는 사람들이 3차원의 존재를 깨닫는 것, 그것이 나의 궁극적인 목표이다. 특히, 나는 오랫동안 ‘A 스퀘어,’ 자네를 3차원의 교리를 충실히 설파할 사도apostle로서 눈여겨 보고 있었다. 자네는 플랫랜드에 살고 있는 많은 주민들과는 다르게 자연의 근본적인 수수께끼들에 대해서 궁금증을 갖고 있더군.”
나는 ‘정신 나간 다각형이군’이라고 생각했다. 어떻게 하면 이 상황을 벗어날 수 있을까 고민하기 시작했다. ‘지금은 바쁘니 나중에 다시 오라고 할까?’ 아니면 ‘미친 소리 그만하고 당장 내 집에서 나가지 않으면 경찰에 신고한다고 할까?’ 여러 가지 생각들이 머릿속을 스치고 지나갔다.
그때 자신을 “스피어”라고 부르는 선분은 다시 말을 이어갔다.
“표정을 보아하니 내 말을 믿지 못하는 모양인데, 당신을 충분히 이해할 수 있다. 이전에 만난 사도들도 처음에는 내 말을 믿지 못했다. 아니 이해하지 못했지. 당신에게 3차원을 이해시키기 위해서 우선 한 가지를 시도해 보자. 나를 한번 만져 보아라.”
호기심은 항상 품위를 이기는 법이라고 했던가? 나는 자신을 “스피어”라고 부르는 선분을 만져 보았다. ‘어라, 모서리가 없다. 이 다각형은 분명히 원이다. 그럼 왕족이란 말인가?’
“이제 내가 변하는 모습을 느껴 보아라.” 자신을 “스피어”라고 부르는 선분, 아니 원이 말했다. 이어 원은 점점 커졌다. 그러고는 다시 작아졌다. 결국 점이라고 부를 수 있을 만큼 작아진 순간, 원은 사라졌다! 유에서 무로 사라진 것이다. 그리고 얼마 후 ‘이제 끝인가’라고 생각한 순간, 원은 다시 나타났다. 무에서 유로 다시 돌아온 것이다.
“자, 어떤가? 내가 어떻게 이러한 일을 할 수 있다고 생각하는가?”
나는 모른다는 표정을 지었다.
이에 자신을 “스피어”라고 부르는 원은 구가 무엇인지 자세하게 설명하기 시작했다. “구는 단면이 다양한 지름을 가지는 원으로 이루어진 입체이다. 너는 방금 내가 플랫랜드를 통과해서 지나갈 때 생기는 나의 여러 단면을 본 것이다. 이해되는가?”
나는 물론 이해되지 않았다.
“이해되지 않는다는 것을 잘 알고 있다. 실망하지 마라. 언제나 그렇듯이 3차원을 이해하는 가장 확실한 방법은 직접 보는 것이다. 자, 이제 위쪽으로 올라가 보자.”
“위쪽이라고요? 북쪽을 말하는 것인가요?”
“아니. 북쪽이 아니라 위쪽으로Upward, not Northward.”
내가 미처 더 물어보기도 전에 자신을 “스피어”라고 부르는 원은 사라졌다. 그리고 나는 알 수 없는 힘에 의해서 어느 방향으로 끌어당겨 졌다. 북쪽이 아니라 위쪽으로.
그다음 순간 나는 플랫랜드를 위에서 아래로 내려다보고 있었다. 이제 3차원 속에서 2차원 평면이 무엇을 의미하는지 깨달을 수 있었다. 아니 그냥 볼 수 있었다. 플랫랜드는 2차원 평면이었다. 내 동족들은 2차원 평면에서 분주히 움직이고 있었다. 이제 그들이 지니는 다각형의 모양을 안개 없이도 쉽게 파악할 수 있었다.
그리고 그 순간 한 줄기 빛이 3차원을 가로질러 플랫랜드에 내리쬐고 있는 것이 보였다. 아, 빛… 눈부시게 아름다운 빛이… 3차원에서 내려오고 있었다.
“이제 이해되는가?” 자신을 “스피어”라고 부르는 원, 아니 구가 물었다.
“네, 알 것 같아요. 이제 모든 것들이 명확하게 보여요. 그리고 무엇보다 너무나 아름다워요…”
“오늘 수업으로는 이제 충분한 것 같군. A 스퀘어, 이제 너는 돌아가서 3차원의 존재를 플랫랜드의 사람들에게 널리 알리도록 해라. 더 높은 차원의 세계가 존재한다는 사실을 알게 되면 플랫랜드에서 벌어지고 있는 수많은 어처구니없는 일들 중에서 전부는 아니더라도 많은 것들이 사라질 것이다. 하지만 조심하게, 나의 사도여. 플랫랜드의 왕가는 이미 3차원의 존재를 알고 있다. 그들은 국민들이 3차원의 존재를 알게 되면 왕가의 권위에 반기를 들 것을 두려워해서 이 사실을 수천 년 동안 철저하게 숨기고 있다. 예전 사도들도 이 사실을 알리려다가 결국 감옥에 처넣어지거나 심지어는 처형당했다. A 스퀘어, 다시 만날 때까지 부디 무사하기를 바라네.”
나는 정신 차릴 틈도 없이 그렇게 다시 플랫랜드로 내려왔다.
이제 어떻게 해야 할까? 플랫랜드의 사람들에게 3차원의 존재를 설파해야 할까? 그렇게 한다고 해서 그들이 제대로 이해할 수 있을까? 이해하지 못한 사람들이 나를 신고하지 않을까? 나도 예전 사도들처럼 감옥에 처넣어질까? 그렇다면 누가 나를 구해줄 것인가?
그리고 설사 플랫랜드의 주민들이 더 높은 차원의 세계가 있다는 것을 알게 된다고 하더라도 그들의 삶이 나아지기는 할 것인가? 오히려 삶의 의미가 없어지는 것은 아닐까? 3차원에 사는 사람들이 보기에 우리는 개미와 같은 하찮은 존재일 것이다. 더 높은 차원의 세계가 있다는 사실을 앎으로써 하찮은 존재가 되는 것이 나을까, 아니면 우리가 사는 익숙한 세계에 나름 만족하면서 중요한 존재로 계속 사는 것이 나을까?
그래도… 그럼에도 불구하고… 아까 본 광경은 정말 눈부시게 아름다웠다. 3차원 공간에서 내려다본 플랫랜드의 모습, 그 아름다운 광경을 본 것만으로도 충분했다. 그것으로 이 모든 걱정, 그리고 앞으로 다가올 곤경은 기꺼이 치를 가치가 있는 것은 아닐까?
재미있게 읽으셨는가? 지금까지 “믿기 힘든 양자 Incredible Quantum” 시리즈를 꾸준히 읽고 있는 독자들은 어리둥절했을 것이다. 앞서 필자는 난생 처음 소설 아닌 소설을 써 보았다. 사실 앞선 글은 필자의 독창적인 소설이 아니라 애드윈 A. 애버트Edwin A. Abbott의 <플랫랜드: 다차원의 서사시Flatland: A Romance of Many Dimensions>라는 소설을 현대적으로 짧게 재구성해 본 것이다.
원소설은 1884년 처음 출간되었는데, 영국 빅토리아 시대Victorian era의 계급주의를 비판하기 위해서 쓰였다. 하지만 아이러니하게도 당대의 남녀 차별적인 시각을 그대로 담고 있어서 논란이 많은 작품이기도 하다. 앞서 필자는 사회철학적인 이슈보다는 “플랫랜드”에 담겨져 있는 차원에 대한 기하학적인 고찰에 집중하고자 했다. 하지만 이러한 고찰은 자기 자신의 세계를 넘어서 더 높은 차원을 상상한다는 것이 얼마나 어려운지를 절절하게 느끼게 해 준다. 사회철학적인 이슈를 딱히 강조하지 않으려고 해도 차원에 대한 고찰은 자연스럽게 우리 인식의 한계를 깨닫게 해 주는 것이다.
그렇다. 더 높은 차원을 상상하는 것은 어렵다. 2차원에 살고 있는 A 스퀘어가 3차원 입체를 잘 이해하지 못하는 것처럼 3차원에 살고 있는 우리가 4차원 입체를 이해하는 것은 어렵다. 얼마나 어려운지 실감하기 위해서 4차원 하이퍼큐브hypercube의 모습을 한번 상상해 보자.
3차원에 살고 있는 우리들이 큐브cube, 즉 정육면체를 상상하는 것은 그리 어렵지 않다. 그냥 네모난 상자의 모습을 머리 속에 떠 올리면 된다. 하지만 바로 한 차원만 높여서 4차원에 존재하는 하이퍼큐브가 3차원에서 어떤 모습으로 나타날지 상상하는 것은 꽤 어렵다.
자, 무엇인가 이해하기 어려울 때에는 비유를 이용하는 것이 좋다. 다시 말해서, 2차원에 살고 있는 A 스퀘어가 3차원 정육면체를 상상하기 위해서 어떻게 해야 하는지 생각해 보자. A 스퀘어에게 정육면체는 모종의 다양한 사각형으로 이루어진 단면들의 집합이다. 비슷하게 생각해 보면, 3차원에 살고 있는 우리에게 하이퍼큐브는 모종의 다양한 정육면체로 이루어진 단면들의 집합이다.
아직도 정확하게 감이 오지 않을 것이다. 조금 더 구체적인 이미지를 얻기 위해서, 마치 스피어가 2차원 플랫랜드를 뚫고 지나가는 것처럼 하이퍼큐브가 3차원 세상을 뚫고 지나간다고 하자. 그렇다면 스피어가 지름이 변하는 원으로 보이는 것처럼 하이퍼큐브는 크기가 변하는 정육면체로 보일 것이다. 즉, 하나의 정육면체는 하이퍼큐브가 어느 주어진 순간에 3차원 세상으로 투영된 단면projected cross section이다. 하이퍼큐브의 전체적인 모습은 이러한 투영된 단면이 시간의 함수로 변하는 모습을 통해서 추정할 수 있다.
[그림2]는 4차원 하이퍼큐브를 0차원에 존재하는 점point으로부터 차근차근 차원을 높여가면서 구성하는 방법을 보여준다. [그림2]에서 볼 수 있듯이 점을 옆으로 이동하면서 생기는 궤적은 1차원에 존재하는 선분이 된다. 그리고 선분을 위로 이동하면서 생기는 궤적은 2차원에 존재하는 사각형이 된다. 이러한 사각형을 다시 앞쪽으로 이동시키면 그 궤적은 3차원에 존재하는 정육면체가 된다. 마지막으로 정육면체를 모종의 4번째 방향으로 이동시키면 4차원 하이퍼큐브가 된다.
참고로, 4차원 하이퍼큐브는 “테서렉트tesseract”라고도 불린다. 테서렉트라는 단어는 최근에 마블 코믹스Marvel Comics가 제작한 영화 <어벤져스Avengers>가 크게 인기를 끌면서 그 이름이 널리 알려졌다. 엄밀하게 말해서 <어벤져스>에 나오는 테서렉트는 4차원 하이퍼큐브와는 직접적으로 아무 상관없는 개념이다. <어벤져스>에 나오는 테서렉트의 원래 이름은 “코스믹 큐브Cosmic Cube”였다. 이후에 코스믹 큐브는 그것이 차원을 넘나드는 신비로운 힘을 지니는 정육면체라는 사실을 강조하기 위해서 테서렉트라는 새로운 이름으로 재탄생하게 되었다.
앞서 차원에 대해서 이런저런 고찰을 해 본 이유는 이제 우리가 고려할 양자역학 문제에서 차원을 높일 때가 되었기 때문이다.
돌이켜 보면 지금까지 우리가 “믿기 힘든 양자 Incredible Quantum” 시리즈를 통해서 구체적으로 풀어 본 문제는 두 상태 문제Two-state problem 밖에 없다. 하지만 두 상태 문제는 간단해 보일지라도 놀라울 정도로 심오하다. “믿기 힘든 양자 Incredible Quantum [7]: 두 상태 이야기”에서 보았듯이 슈뢰딩거의 고양이라는 두 상태 문제는 양자역학적인 중첩 상태가 얼마나 우리의 직관에 반할 수 있는지 보여 준다. 그리고 “믿기 힘든 양자 Incredible Quantum [8]: 위상의 귀환”에서 보았듯이 이러한 중첩 상태가 차지하는 가상 공간에는 자기 홀극magnetic monopole이 존재한다. 놀라운 사실은 자기 홀극이 실공간real space이 아니라 가상 공간에 존재할지라도 실제로 위상 절연체와 같은 새로운 양자물질 상태를 발생시킬 수 있다는 것이다. 마지막으로, “믿기 힘든 양자 Incredible Quantum [9]: 양자 얽힘”에 설명했듯이 양자역학적인 중첩 현상은 양자 텔레포테이션quantum teleportation이나 양자 컴퓨터quantum computer와 같은 놀라운 응용의 핵심 원리를 제공한다.
물론 우주에 존재하는 물질은 아무리 작더라도 일반적으로 두 개 이상의 많은 상태를 가진다. 많은 상태의 존재는 파동 함수가 존재하는 힐버트 공간Hilbert space의 차원이 높아진다는 것을 의미한다.
이제 우리는 더 높은 차원의 문제를 생각하기 위해서 상상력을 발휘해야 한다.
많은 상태 이야기
우선 상태의 숫자에 의해서 결정되는 힐버트 공간의 차원과 입자의 운동 방향에 의해서 결정되는 실공간의 차원은 다르다.
“믿기 힘든 양자 Incredible Quantum [7]: 두 상태 이야기”에서 보았듯이 두 상태를 가지는 힐버트 공간에 존재하는 임의의 상태는 2개의 각도를 정하면 완벽하게 규정된다. 따라서 이 경우에 힐버트 공간의 차원은 2차원이라고 할 수 있다. 하지만 실공간의 입장에서 보면 두 상태 문제는 단순히 W 모양의 퍼텐셜 우물에서 왼쪽과 오른쪽 점 사이를 왔다 갔다 하는 입자의 동역학을 기술하는 문제이다. 따라서 실공간의 입장에서 보면 두 상태 문제는 “거의 0차원” 문제라고 할 수 있다.
진정한 의미에서 실공간 1차원 문제는 입자가 뛰어다닐 수 있는 점이 무수히 많이 일렬로 나열되어 있는 문제이다. 이 문제는 규칙적인 주기성을 가지는 격자 내에서 전자가 움직여 다니는 문제, 즉 고체 물리의 가장 단순한 문제가 된다. 자, 이제 이 문제를 어떻게 풀 수 있나 생각해 보자.
구체적으로, 입자가 제일 첫 번째 점에 위치하는 상태를 \(|1\rangle\)이라고 하자. 비슷하게 두 번째, 세 번째 점에 위치하는 상태를 각각 \(|2\rangle\)와 \(|3\rangle\)이라고 하자. 일반적으로는 \(n\)번째 점에 위치하는 상태를 \(|n\rangle\)이라고 할 수 있다. 벡터 형식으로 표현하면 각 상태는 다음과 같이 쓰인다.
\(|1\rangle=
\left(
\begin{array}{c}
1 \\ 0 \\ 0 \\ \vdots
\end{array}
\right), \;\;
|2\rangle=
\left(
\begin{array}{c}
0 \\ 1 \\ 0 \\ \vdots
\end{array}
\right), \;\;
|3\rangle=
\left(
\begin{array}{c}
0 \\ 0 \\ 1 \\ \vdots
\end{array}
\right), \;\;
\cdots \)
이제 입자가 1차원 격자 상의 주어진 위치에서 그 주변 바로 앞뒤의 점으로 뛰어다닐 수 있다고 하자. 이러한 상황을 기술하는 해밀토니안은 다음과 같이 쓰인다.
\(H=-t \sum_{n=1}^{N-1} \left(c^\dagger_{n+1}c_n +c^\dagger_n c_{n+1}\right)\)
여기서 \(c_n\)은 \(n\)번째 점에 존재하는 입자를 소멸시키는 연산자, 즉 소멸 연산자annihilation operator이고, \(c^\dagger_n\)은 \(n\)번째 점에 입자를 새롭게 생성시키는 연산자, 즉 생성 연산자creation operator이다. 이제 소멸 연산자와 생성 연산자를 적절하게 잘 결합하면 입자의 위치를 격자 상에서 앞뒤로 한 칸 움직이는 연산자를 만들 수 있다. 즉, \(c^\dagger_{n+1}c_n\)은 \(n\)번째 점에 존재하는 입자를 \(n+1\)번째 점으로 이동시키는 연산자이고, \(c^\dagger_n c_{n+1}\)은 이와 정확히 반대로 이동시키는 연산자이다.
참고로, 위에서 \(t\)는 시간이 아니라, “믿기 힘든 양자 Incredible Quantum [7]: 두 상태 이야기”에서 이미 언급한 바 있는 “뜀 계수hopping parameter”이다. 뜀 계수는 입자가 얼마나 잘 뛰어다니는지를 결정하는 물리량이다. 물리적으로 말해서, 뜀 계수는 질량의 역수로 생각하면 된다. 뜀 계수 앞에 음의 부호를 붙인 이유는 나중에 보겠지만 가만히 멈추어 있는 것보다 뛰어다닐수록 운동 에너지가 높아지게 하기 위함이다.
이제 우리가 해야 할 일은 위 해밀토니안을 대각화diagonalization해서 에너지 고유 상태energy eigenstate를 찾는 일이다. 해밀토니안을 대각화하는 데에는 여러 다양한 방법이 있겠지만, 우리가 현재 유일하게 아는 방법은 해밀토니안을 실제로 행렬 형식으로 표현한 다음에 대각화 방정식을 푸는 것이다.
자, 그러기 위해서 해밀토니안을 실제 행렬 형식으로 표현해 보자.
\(H=-t\left[\begin{array}{ccccccc}0 & {\color{red}1} & 0 & & 0 & 0 & 0 \\{\color{red}1} & 0 & {\color{red}1} & \cdots & 0 & 0 & 0 \\0 & {\color{red}1} & 0 & & 0 & 0 & 0 \\& \vdots & & \ddots & & \vdots & \\0 & 0 & 0 & & 0 & {\color{red}1} & 0 \\0 & 0 & 0 & \cdots & {\color{red}1} & 0 & {\color{red}1} \\0 & 0 & 0 & & 0 & {\color{red}1} & 0 \\\end{array}\right]\)
1차원 격자에 존재하는 점의 전체 개수가 \(N\)이라고 할 때, 위 해밀토니안은 \(N\times N\) 정사각 행렬square lattice이다. 참고로 위 행렬에서 \(0\)이 아닌 원소들은 행렬의 대각선에 바로 이웃하는 옆 줄에만 존재한다. 위 행렬이 맞다는 사실은 앞서 벡터로 표현된 각각의 상태를 넣어 보면 알 수 있다. 이렇게 대각선의 원소와 그 대각선에 바로 이웃하는 원소만이 \(0\)이 아닌 행렬을 특별히 “3중 대각 행렬tridiagonal matrix”라고 부른다. 결론적으로는 우리는 3중 대각 행렬을 진정한 대각 행렬diagonal matrix로 만들어야 한다.
구체적으로, 위 해밀토니안은 다음과 같은 대각화 방정식을 풀어서 대각화할 수 있다.
\(D_N={\rm det}(H-\lambda I)={\rm det}\left[
\begin{array}{ccccccc}
{\color{red}{-\lambda}} & {\color{red}{-t}} & 0 & & 0 & 0 & 0 \\
{\color{red}{-t}} & {\color{red}{-\lambda}} & {\color{red}{-t}} & \cdots & 0 & 0 & 0 \\
0 & {\color{red}{-t}} & {\color{red}{-\lambda}} & & 0 & 0 & 0 \\
& \vdots & & \ddots & & \vdots & \\
0 & 0 & 0 & & {\color{red}{-\lambda}} & {\color{red}{-t}} & 0 \\
0 & 0 & 0 & \cdots & {\color{red}{-t}} & {\color{red}{-\lambda}} & {\color{red}{-t}} \\
0 & 0 & 0 & & 0 & {\color{red}{-t}} & {\color{red}{-\lambda}} \\
\end{array}
\right]
=0\)
여기서 \(\lambda\)는 에너지 고유값energy eigenvalue이다.
드디어 우리가 이제까지 접하지 못했던 새로운 방정식이 나왔다. 도대체 이 방정식은 어떻게 풀어야 할까? 참고로 위에서 행렬식이 0이 되는 조건을 찾아야 하는 행렬은 여전히 3중 대각 행렬이다. 바로 이 성질로 인해서 위 방정식은 정확하게 풀릴 수 있게 된다.
여기서 자세한 유도 과정을 보여 줄 수는 없지만, 행렬식determinant의 기본 성질에 의해서 앞선 대각화 방정식은 다음과 같은 “점화식recurrence relation”을 만족한다.
\(D_N= -\lambda D_{N-1} -t^2 D_{N-2}\)
다시 말해서, \(N\)개의 격자점을 가지는 1차원 격자 문제의 행렬식은 \(N-1\)과 \(N-2\)개의 격자점을 위한 행렬식과 연결된다. 참고로 점화식의 “초기 조건initial condition”을 규정하는 \(D_0\)과 \(D_1\)는 다음과 같이 주어진다.
\(D_0=1, \;\; D_1=-\lambda\)
보통 고등학교 수학 시간에 배우는 등차 혹은 등비 수열의 점화식보다 복잡하기는 하지만 놀랍게도 위 점화식은 정확하게 풀린다.
구체적으로 우리는 점화식을 풀기 위해서는 상상력을 발휘해야 한다. 즉, 정답의 형태를 잘 추측해야 한다. 여러 가능성이 있을 수 있겠으나, 점화식의 형태를 꼼꼼히 잘 살펴 보다가 보면 \(D_N\)이 모종의 멱급수power series로 주어진다고 추측해 볼 수 있다.
\(D_N=r^N\)
위 추측을 실제로 점화식에 대입해 보자.
\(r^N+\lambda r^{N-1} +t^2 r^{N-2} =0\)
그렇다면 위 방정식이 만족되기 위해서 \(r\)은 다음의 2차 방정식을 만족해야 한다.
\(r^2+\lambda r +t^2 =0\)
물론 \(r\)은 2차 방정식의 근의 공식에 의해서 다음의 2개의 값을 가질 수 있다.
\(r_\pm = \frac{1}{2} \left(-\lambda\pm\sqrt{\lambda^2-4t^2}\right)\)
일반적으로 \(D_N\)은 이렇게 서로 다른 2개의 해 \(r_\pm\)가 주는 멱급수를 적절하게 결합해서 만들어 낼 수 있다.
\(D_N=a r^N_{+} +b r^N_{-}\)
여기서 \(a, b\)는 적절한 상수로서 초기 조건, \(D_0=1, D_1=-\lambda\)에 의해서 결정된다.
결론적으로 초기 조건을 만족하는 최종적인 해는 다음과 같이 얻어진다.
\(D_N=\frac{1}{\sqrt{\lambda^2-4t^2}}\left(r^{N+1}_{+}-r^{N+1}_{-}\right)\)
이제 우리에게 주어진 일은 \(D_N=0\)을 만족하는 에너지 고유값 \(\lambda\)를 찾는 것이다. 다시 말해서, 다음의 방정식을 만족하는 \(\lambda\)를 찾으면 된다.
\(\left(\frac{r_+}{r_-}\right)^{N+1}=1\)
즉, \(\lambda\)는 다음의 방정식을 만족한다.
\(\frac{r_+}{r_-}=e^{i\frac{2\pi p}{N+1}}=\frac{\lambda-\sqrt{\lambda^2-4t^2}}{\lambda+\sqrt{\lambda^2-4t^2}}\)
여기서 \(p\)는 \(1\)과 \(N\) 사이의 임의의 정수이다.
약간의 대수 작업을 거치면 최종적으로 에너지 고유값은 다음과 같이 얻어진다.
\(\lambda= -2t \cos{\left( \frac{\pi p}{N+1} \right)}\)
편의상 에너지 고유값을 새로운 변수 \(k=\pi p/(N+1)\)을 도입해서 다음과 같이 다시 써 보자.
\(\lambda=-2t\cos{k}\)
물리학자가 위 공식을 본다면 이것이 1차원 격자 위에서 움직이는 파동의 에너지-파수 관계식, 즉 분산 관계식dispersion relation임을 즉각적으로 알 수 있다.
사실 지금까지 전문적인 물리학자가 이 글을 읽고 있었다면 이 문제를 굳이 왜 이렇게 어렵게 푸는지 의문을 가졌을 것이다. 아래 보겠지만 훨씬 더 쉬운 방법이 존재하기 때문이다. 하지만 이 쉬운 방법에 대해서 설명하기 전에, 우리의 현재 방법 내에서 새로운 변수 \(k\)가 정말 1차원 격자 위에 움직이는 파동의 파수wave number라는 사실을 증명해 보자.
새로운 변수 \(k\)의 의미를 알기 위해서는 위 에너지 고유값을 가지는 에너지 고유상태energy eigenstate를 구해야 한다. 즉, 다음의 연립 방정식을 만족하는 계수 \(u_n\)들을 찾아야 한다. (고유상태에 대한 기억을 되살리기 위해서는 “믿기 힘든 양자 Incredible Quantum [7]: 두 상태 이야기”를 참조하기를 바란다.)
\(\left[\begin{array}{ccccccc}{\color{red}{-\lambda}} & {\color{red}{-t}} & 0 & & 0 & 0 & 0 \\{\color{red}{-t}} & {\color{red}{-\lambda}} & {\color{red}{-t}} & \cdots & 0 & 0 & 0 \\0 & {\color{red}{-t}} & {\color{red}{-\lambda}} & & 0 & 0 & 0 \\& \vdots & & \ddots & & \vdots & \\0 & 0 & 0 & & {\color{red}{-\lambda}} & {\color{red}{-t}} & 0 \\0 & 0 & 0 & \cdots & {\color{red}{-t}} & {\color{red}{-\lambda}} & {\color{red}{-t}} \\0 & 0 & 0 & & 0 & {\color{red}{-t}} & {\color{red}{-\lambda}} \\\end{array}\right]\left(\begin{array}{c}u_1 \\ u_2 \\ u_3 \\ \vdots \\ u_{N-2} \\ u_{N-1} \\ u_{N}\end{array}\right)=0\)
위 연립 방정식은 개별 방정식으로 다시 표현할 수 있다. 즉, \(n\)이 \(1\)보다 크고 \(N\)보다 작으면 다음과 같다.
\(u_{n+1}+\frac{\lambda}{t} u_n+u_{n-1}=0\)
반면에 \(n\)이 \(1\)이거나 \(N\)이면 다음과 같다.
\(u_2+\frac{\lambda}{t} u_1=0\)
\(u_{N-1}+\frac{\lambda}{t} u_N=0\)
“믿기 힘든 양자 Incredible Quantum [7]: 두 상태 이야기”에서 설명했듯이 에너지 고유상태를 위한 연립 방정식 중의 하나는 에너지 고유값을 얻어지는 조건으로 인해서 자동으로 만족하게 된다. 예를 들어서, 위 방정식들 중에서 \(n=N\)의 경우에 해당하는 방정식은 따로 풀 필요가 없다.
그런데 그렇게 되면 에너지 고유상태의 계수인 \(u_n\)들을 모두 결정하기 위해서 여분의 방정식 하나가 더 필요하게 된다. 이 여분의 방정식은 바로 에너지 고유상태(사실 임의의 모든 파동 함수)가 규격화되어야 한다는 조건이다. 즉, 파동 함수의 절대값의 제곱이 1이 되어야 한다.
\(\sum_{n=1}^{N} |u_n|^2=1\)
하지만 이 조건은 전체 계수들에 적절한 규격화 상수normalization constant를 곱하면 된다는 것을 의미하므로 이 단계에서는 편의상 \(u_1=1\)로 놓고 나중에 규격화 상수를 찾아서 곱하기로 하자.
결론적으로 우리가 풀어야 하는 방정식은 2개의 초기 조건 \(u_1=1\)과 \(u_2= -\lambda/t\)을 만족하는 계수들의 점화식이다. 편의상 앞선 점화식을 다시 써 보자.
\(u_{n+1}+\frac{\lambda}{t}u_n +u_{n-1}=0\)
위 점화식의 해는 앞에서 에너지 고유값을 구하기 위해서 썼던 방법과 유사한 방법을 쓰면 다음과 같이 추정할 수 있다.
\(u_n=A \omega^n +B (\omega^*)^n\)
여기서 \(\omega\)와 \(\omega^*\)는 다음 방정식의 해이다.
\(x^2+\frac{\lambda}{t}x+1=0\)
이제 앞서 얻은 에너지 고유값이 \(\lambda=-2t\cos{k}\)라는 결과를 이용하면 \(\omega=e^{ik}\)이라는 사실을 알 수 있다. 물론 켤레 복소수의 성질로 인해서 \(\omega^*=e^{-ik}\)이다. 이 사실을 이용해서 에너지 고유상태의 계수를 다시 쓰면 다음과 같다.
\(u_n=A e^{ink} +B e^{-ink}\)
위 \(A, B\)는 앞서 언급한 2개의 초기 조건으로부터 결정된다.
초기 조건을 만족시키기 위해서 결정된 \(A, B\)를 이용해서 에너지 고유상태의 계수를 다시 쓰면 다음과 같다.
\(u_n=\frac{\sin{(nk)}}{\sin{k}}\)
이제 마지막으로 적절한 규격화 상수를 곱하면 에너지 고유상태는 최종적으로 다음과 같이 얻어진다.
\(u_n=\frac{\sin{(nk)}}{\sqrt{\sum_{l=1}^N\sin^2{(lk)}}}\)
자, 이제 에너지 고유상태가 어떻게 생겼는지 그림이 그려지는가? 에너지 고유상태는 마치 줄넘기 줄의 양쪽 끝부분을 고정하고 흔들 때 출렁거리면서 생기는 파동과 같다. 새로운 변수 \(k\)는 정말 1차원 파동의 파수인 것이다! 참고로 [그림3]은 파수 \(k\)의 함수로 출렁거리는 에너지 고유상태의 변화를 보여준다.
그런데 앞에서 잠깐 언급했듯이, 위와 같이 해밀토니안을 곧이곧대로 대각화해서 격자 문제의 에너지 고유값을 얻고, 그다음 단계로 에너지 고유상태를 얻는 방법 말고 휠씬 더 쉬운 방법이 존재한다. 그것은 푸는 순서를 뒤집는 것이다!
구체적으로 말해서, 우선 격자 문제의 에너지 고유상태가 파동이라고 가정하자. 그리고 나서 그 답이 맞는지 해밀토니안에 넣어서 확인해 보자. 파동이라는 가정이 맞는다면 에너지 고유값은 손쉽게 구할 수 있다. 물론 에너지 고유상태는 이미 찾아져 있다.
격자 문제에 있어서 에너지 고유 상태가 되는 파동에는 특별한 이름이 붙어있다. 그 이름은 블로흐 파동Bloch wave이다.
블로흐 파동
1차원 격자 위에서 움직이는 입자를 기술하는 해밀토니안으로 다시 돌아가 보자.
\(H=-t \sum_{n=1}^N \left(c^\dagger_{n+1} c_n + c^\dagger_n c_{n+1}\right)\)
이제부터 편의상 격자의 맨 마지막 점을 지나가면 다시 첫 번째 점으로 되돌아오는 특별한 경계 조건boundary condition을 쓰도록 하자. 이러한 경계 조건을 “주기적 경계 조건periodic boundary condition”이라고 부른다. 구체적으로, 우리의 현재 문제에 있어서 주기적 경계 조건은 다음과 같이 쓰인다.
\(|N+1\rangle=|1\rangle\)
다시 말해서 \(N+1\)번째 점은 첫 번째 점과 같다. 참고로, 다시 한번, \(|n\rangle\)은 입자가 \(n\)번째 점에 위치하는 상태를 의미한다. 주기적 경계 조건이 의미하는 바는 1차원 격자 위에 있는 각 점이 진주라고 할 때 진주들을 연결해서 고리 모양의 진주 목걸이를 만든다는 것이다.
이제 “믿기 힘든 양자 Incredible Quantum [6]: 양자 삼위일체 2부”에서 설명한 브라-켓 표기법(bra-ket notation)을 사용해서 “이동 연산자” \(c^\dagger_{n+1}c_n\)과 \(c^\dagger_n c_{n+1}\)을 다음과 같이 표현해 보자.
\(c^\dagger_{n+1}c_n =|n+1\rangle \langle n|\)
\(c^\dagger_{n}c_{n+1} =|n\rangle \langle n+1|\)
이동 연산자를 위와 같이 브라-켓으로 표현하는 방식은 처음에는 조금 어색할 수 있지만 조금 생각해 보면 어렵지 않게 이해할 수 있다. 예를 들어서, \(c^\dagger_{n+1}c_n =|n+1\rangle \langle n|\)라는 표현을 이해해 보자. 오른쪽에 있는 브라 \(\langle n|\)은 만약에 \(|n\rangle\)이 오른쪽에서 작용한다면 그것을 없애고 왼쪽에 있는 켓 \(|n+1\rangle\)으로 만든다. 그런데 이것은 이동 연산자가 수행하는 작업과 정확히 같다.
\(c^\dagger_{n+1}c_n |n\rangle=|n+1\rangle \langle n|\cdot |n\rangle=|n+1\rangle\)
반대의 경우인 \(c^\dagger_{n}c_{n+1} =|n\rangle \langle n+1|\)도 이와 비슷하게 이해할 수 있다.
이제 이동 연산자를 다음과 같이 정식으로 정의해 보자.
\(T_{+} = \sum_{n=1}^N |n+1\rangle\langle n|\)
\(T_{-} = \sum_{n=1}^N |n\rangle\langle n+1|\)
위에서 \(T_{+}\)와 \(T_{-}\)는 각각 입자의 위치를 앞과 뒤로 한 칸씩 이동시키는, 즉 전진 및 후진 연산자이다. 해밀토니안은 이 두 이동 연산자의 합이다.
\(H= -t (T_{+}+T_{-})\)
자, 이제 우리가 추측하는 에너지 고유상태는 출렁거리는 파동을 기술하는 상태이다. 앞에서 이러한 격자 속의 파동을 블로흐 파동이라고 부른다고 했다. 블로흐 파동을 기술하기 위해서 우리는 다음과 같은 파동 함수를 시도할 수 있다.
\(|k\rangle=\frac{1}{\sqrt{N}} \sum_{n=1}^N e^{ikn} |n\rangle\)
위에서 전체 계수 \(1/\sqrt{N}\)는 규격화 조건으로부터 결정된다. 그리고 잘 생각해 보면 파수 \(k\)는 주기적 경계 조건에 의해서 다음과 같이 양자화되어야 한다.
\(k=\frac{2\pi}{N}p\)
위에서 \(p\)는 \(1\)과 \(N\) 사이의 임의의 정수이다. 다른 말로 하면, 블로흐 파동이 격자의 각 점에서 가지는 계수, 즉 파동 함수의 진폭amplitude는 다음과 같이 주어진다.
\(u_n=\frac{1}{\sqrt{N}}e^{ikn}\)
이제, 블로흐 파동이 정말 에너지 고유상태인지 확인해 보자. 그러기 위해서, 우선, 전진 연산자 \(T_{+}\)가 블로흐 파동에 작용하면 어떤 일이 벌어지는지 알아보자.
\(T_{+}|k\rangle = \frac{1}{\sqrt{N}} \sum_{n=1}^N e^{ikn} T_{+} |n\rangle=\frac{1}{\sqrt{N}} \sum_{n=1}^N e^{ikn}|n+1\rangle=\frac{1}{\sqrt{N}} \sum_{n=1}^N e^{-ik}e^{ik(n+1)}|n+1\rangle=e^{-ik}|k\rangle\)
위에서 맨 마지막 등식은 주기적 경계 조건에 의해서 성립된다. 비슷하게, 후진 연산자 \(T_{-}\)가 블로흐 파동에 작용하면 다음과 같은 일이 벌어진다.
\(T_{-}|k\rangle=e^{ik}|k\rangle\)
결론적으로 해밀토니안을 블로흐 파동에 작용하면 다음과 같이 된다.
\(H|k\rangle=-t(T_{+}+T_{-})|k\rangle=-2t\cos{k}|k\rangle\)
즉, 블로흐 파동은 에너지 고유값 \(\epsilon_k\)를 가지는 에너지 고유상태이다. 이때 에너지 고유값 \(\epsilon_k\)와 파수 \(k\)의 관계, 즉 분산 관계식은 다음과 같이 주어진다.
\(\epsilon_k=-2t\cos{k}\)
우리가 얻은 분산 관계식은 앞에서 구한 공식과 정확히 같다! 엄밀하게 말해서, 파수의 양자화 조건만 빼고는 정확히 같다.
파수의 양자화 조건이 다른 것은 다른 경계 조건이 쓰였기 때문이다. 바로 위에서는 물론 주기적 경계 조건이 쓰였다. 그렇다면 이전에 해밀토니안을 직접 대각화해서 풀 때는 어떤 경계 조건이 쓰였던 것일까?
잘 살펴보면, 이전에 직접 대각화 방법을 통해서 얻은 파동 함수의 계수는 앞으로 이동하는 블로흐 파동 \(e^{ikn}\)과 뒤로 이동하는 블로흐 파동 \(e^{-ikn}\)의 합으로 주어졌다는 사실을 알 수 있다. 그리고 이 합은 다름 아니라 사인sine 함수였다. 이 상황에서 경계 조건은 마치 가상으로 \(0\)과 \(N+1\)번째 점이 존재하고 그 점에서 파동 함수의 진폭이 \(0\)이 되는 조건으로 볼 수 있다. 참고로 이러한 경계 조건을 “닫힌 경계 조건closed boundary condition”이라고 부른다. 결국, 앞에서 직접 대각화를 통해서 얻은 에너지 고유상태는 닫힌 경계 조건을 만족하는 블로흐 파동의 적절한 조합으로 이해할 수 있다!
나중의 논의를 위해서 같은 문제를 다시 한번 다르게 풀어 보자. 이번에는 블로흐 파동을 이용해서 해밀토니안 자체를 변형해 보고자 한다. 우선, 앞에서 설명했듯이 해밀토니안은 브라-켓 표기법으로 다음과 같이 쓰일 수 있다.
\(H=-t\sum_{n=1}^N \left(|n+1\rangle\langle n| +|n\rangle\langle n+1|\right)\)
이제 역 푸리에 변환inverse Fourier transform을 이용하면 입자가 주어진 위치에 존재하는 상태 \(|n\rangle\)을 블로흐 파동 상태 \(|k\rangle\)로 다음과 같이 표현할 수 있다.
\(|n\rangle=\frac{1}{\sqrt{N}}\sum_k e^{-ikn} |k\rangle\)
위에서 파수 \(k\)에 대한 합은 양자화 조건을 만족하는 모든 파수 값에 대해서 합을 취한다는 것을 의미한다.
위 공식을 해밀토니안에 집어 넣고 약간 정리하면 다음과 같은 결과를 얻을 수 있다.
\(H=-t\sum_{k, k^\prime} \left[\delta(k-k^\prime)e^{-ik^\prime} |k^\prime\rangle\langle k|+\delta(k^\prime-k)e^{ik^\prime} |k^\prime\rangle\langle k|\right]\)
여기서 \(\delta(\Delta k)\)는 다음과 같이 정의된다.
\(\delta(\Delta k)=\frac{1}{N} \sum_{n=1}^N e^{i\Delta k n}=\frac{1}{N} e^{i(N+1)\Delta k/2}\frac{\sin{(N\Delta k/2)}}{\sin{(\Delta k/2)}}\)
위에서 두 번째 등식은 등비수열의 합의 공식을 통해서 얻어진다. 위에 주어진 함수 \(\delta(\Delta k)\)는 \(\Delta k\)가 주기적 경계 조건을 만족하는 경우에 기본적으로 크로네커 델타Kronecker delta가 된다. 다시 말해서 \(\delta(\Delta k)\)는 \(\Delta k=0\)일 경우에는 \(1\)이 되고, 나머지 모든 경우에는 \(0\)이 되는 함수이다. 참고로 위 함수는 푸리에 변환 이론에서 중요한 역할을 하는 “디리클레 핵Dirichlet kernel”이다.
크로네커 델타의 성질을 이용해서 해밀토니안을 정리하면 다음과 같이 깔끔해진다.
\(H=-2t\sum_k \cos{k} |k\rangle\langle k|\)
위 공식은 다름 아니라 블로흐 파동이 에너지 고유상태이며 그것의 에너지 고유값은 앞에서 구한 공식 \(\epsilon_k =-2t\cos{k}\)에 의해서 주어진다는 것을 의미한다.
지금까지 우리는 하나의 1차원 격자 문제를 서로 다른 세 가지 방법을 써서 풀어 보았다. 이렇게 같은 문제를 여러 번 풀어 본 이유는 블로흐 파동에 익숙해지기 위해서이다. 가장 간단한 시스템인 1차원 격자를 완벽하게 이해한 후에 우리는 본격적으로 재미있는 문제들에 도전할 수 있다. 이제 우리가 도전할 문제는 1차원 격자에서 발생하는 위상 절연체topological insulator와 2차원 벌집 격자honeycomb lattice에서 발생하는 그래핀graphene이다.
두 에너지띠 이야기: 어쩌다 위상 절연체
필자는 “믿기 힘든 양자 Incredible Quantum [8]: 위상의 귀환”에서 위상 절연체에 대해서 이야기를 했다. 그때로 돌아가서 다시 논의 내용을 읽어 보면 위상 절연체는 2차원에서 발생하는 것이 매우 자연스럽다는 사실을 깨달을 수 있다.
사실 2차원에서 발생하는 위상 절연체를 3차원으로 확장하는 문제는 위상물질 분야가 초창기에 태동할 때 매우 중요한 문제였다. 이 문제는 처음에 쉽게 해결되지 않았지만, 각고의 노력 끝에 결국 해결 방법이 발견되게 된다. 불행히도 여기서 이 해결 방법에 대해서 자세하게 이야기할 수는 없다. 대신 이번 섹션에서는 오히려 차원을 하나 내려서 1차원 격자에서 발생하는 위상 절연체에 대해서 이야기해 보고자 한다.
1차원 위상 절연체를 기술하는 해밀토니안은 생각보다 무척 단순하다. 구체적으로, 앞선 섹션에서 논의한 1차원 격자 문제에서 뜀 계수가 번갈아 가면서 다른 값을 가지는 경우로 확장해 보자. 물리적으로는 2개의 서로 다른 원자들이 격자 구조를 만들고 그 위를 전자가 움직여 다니는 상황으로 생각할 수 있다. 편의상 이렇게 서로 다른 원자를 각각 \(A\)와 \(B\) 원자라고 하자. [그림4]를 참조하라.
이 상황을 기술하는 해밀토니안은 생성 및 소멸 연산자를 사용해서 표현하면 다음과 같다.
\(H= -t\sum_n (c^\dagger_{A,n}c_{B,n}+c^\dagger_{B,n}c_{A,n})-t^\prime\sum_n (c^\dagger_{A,n+1}c_{B,n}+c^\dagger_{B,n}c_{A,n+1})\)
위에서 \(n\)은 주어진 \(A\)와 \(B\) 원자 한 쌍으로 이루어진 하나의 단위 격자unit cell의 위치를 표시하는 변수이다. 참고로 위에서 표현된 수식에서 주기적 경계 조건이 암묵적으로 쓰였다.
위 해밀토니안은 처음 보면 쉽게 풀리지 않을 것 같지만, 앞선 섹션에서 배운 푸리에 변환 방법을 이용하면 생각보다 쉽게 풀린다. 그러기 위해서 다음과 같은 푸리에 변환을 생각해 보자.
\(c^\dagger_{A/B,n}=\frac{1}{\sqrt{N/2}} \sum_k e^{ikn} c^\dagger_{A/B,k}\)
위에서 \(c^\dagger_{A/B,k}\)는 각각 \(A\)와 \(B\) 원자로 이루어진 블로흐 파동을 만들어 내는 생성 연산자이다. 위 관계식에 “믿기 힘든 양자 Incredible Quantum [6]: 양자 삼위일체 2부”에서 배운 에르미트 켤레Hermitian conjugate를 취하면 소멸 연산자를 위한 푸리에 변환 관계식을 다음과 같이 얻을 수 있다.
\(c_{A/B,n}=\frac{1}{\sqrt{N/2}} \sum_k e^{-ikn} c_{A/B,k}\)
이제 앞선 해밀토니안을 블로흐 파동의 생성 및 소멸 연산자로 쓰면 다음과 같이 깔끔한 형태로 표현된다.
\(H=\sum_k(\begin{array}{cc}c^\dagger_{A,k} & c^\dagger_{B,k}\end{array})\hat{H}_k\left(\begin{array}{c}c_{A,k} \\ c_{B,k}\end{array}\right)\)
위 해밀토니안 공식 안에 있는 \(2\times 2\) 행렬인 \(\hat{H}_k\)는 다음과 같이 주어진다.
\(\hat{H}_k=\left(\begin{array}{cc}0 & \Delta_k \\\Delta^*_k & 0 \\\end{array}\right)\)
여기서 \(\Delta_k\)는 다음과 같이 정의된다.
\(\Delta_k= -t -t^\prime e^{ik}\)
항상 그렇듯이 에너지 고유 상태를 찾기 위해서는 위 해밀토니안, 구체적으로 \(\hat{H}_k\)를 대각화해야 한다. 다행히 위 해밀토니안은 기본적으로 “믿기 힘든 양자 Incredible Quantum [7]: 두 상태 이야기”에서 대각화해 본 적이 있는 \(2\times 2\) 행렬이다. 즉, \(\hat{H}_k\)를 대각화하면 다음과 같은 에너지 고유값을 얻을 수 있다.
\(\epsilon_k = \pm |\Delta_k|=\pm \sqrt{t^2+t^{\prime 2}+2t t^\prime \cos{k}}\)
위 공식에서 알 수 있듯이 에너지 고유값은 \(t\)와 \(t^\prime\)가 정확히 같지 않으면 유한한 간격gap으로 분리된 2개의 띠band로 구성된다. 이러한 에너지 고유값의 띠를 줄여서 에너지띠energy band라고 부른다.
여기서 잠깐 멈추어 에너지띠의 물리적 의미를 생각해 보자. 격자 내에서 움직이는 전자는 임의의 운동 에너지 값을 다 가질 수 없다. 격자 내에서는 격자 구조에 따라 결정되는 특정한 범위의 운동 에너지만이 허용된다. 이러한 에너지 범위는 유한한 간격으로 분리되어 여러 개가 존재할 수 있는데, 앞선 문제에서는 2개의 에너지띠가 존재하는 것이다.
재미있는 사실은 이미 언급했듯이 앞선 문제가 위상 절연체를 기술할 수 있다는 것이다. 구체적으로, 같은 절연체라고 할지라도 \(t\)와 \(t^\prime\)의 상대적인 크기에 따라서 보통 절연체가 될 수도 있고 위상 절연체가 될 수도 있다.
이 사실을 이해하기 위해서 “믿기 힘든 양자 Incredible Quantum [8]: 위상의 귀환”에서 배운 교훈을 기억해 보자. 우선 두 에너지띠를 기술하는 해밀토니안은 일반적으로 다음과 같은 제만 해밀토니안의 형태로 표현될 수 있다.
\(\hat{H}_{\bf k}={\bf R}_{\bf k} \cdot \boldsymbol{\sigma}\)
여기서 중요한 사실은 \({\bf R}=0\)가 되는 원점에 자기 홀극이 존재한다는 점이다. “믿기 힘든 양자 Incredible Quantum [8]: 위상의 귀환”에서 배운 교훈에 따르면, 위상학적으로 뻔하지 않은 절연체와 뻔한 절연체는 \({\bf R}_{\bf k}\)가 운동량 \({\bf k}\)의 함수로 “보자기”를 형성한다고 할 때, 이 보자기가 자기 홀극을 감쌀 수 있는지 없는지에 따라서 구분된다.
불행히도 위에서 언급한 위상학적인 구분 방법은 현재 우리 문제에 그대로 적용될 수 없다. 왜냐하면 우리 문제가 1차원 문제이기 때문이다. 다시 말해서, 운동량 \({\bf k}\)가 2차원 벡터 \((k_x,k_y)\)가 아니라 단 하나의 숫자 \(k\)로 기술되기 때문이다. 이러한 상황에서 \({\bf R}_{\bf k}\)는 운동량의 함수로 2차원 “보자기”를 형성하는 것이 아니라 1차원 “고리”를 형성하게 된다. 고리로는 자기 홀극에서 나오는 자기장을 완전히 감싸서 가둔다는 것이 불가능하다.
그런데 곰곰이 생각해 보면 여전히 적용 가능한 위상학적인 구분 방법이 존재한다. 구체적으로, 앞선 기술된 해밀토니안의 경우에 \({\bf R}_{\bf k}\)는 다음과 같이 주어진다.
\({\bf R}_{\bf k} = ({\rm Re}\Delta_k, -{\rm Im}\Delta_k, 0)\)
위 공식에 따르면 \({\bf R}_{\bf k}\)가 형성하는 고리는 자기 홀극, 즉 원점을 품고 있는 2차원 평면 위에 놓이게 된다. 이 2차원 평면 위에서 \({\bf R}_{\bf k}\)가 형성할 수 있는 고리는 두 가지 경우 중의 하나이다. 즉, 원점을 감싸거나 감싸지 않거나.
예상했겠지만, 원점을 감싸는 경우는 위상학적으로 뻔하지 않은 절연체, 즉 위상 절연체이고, 감싸지 않는 경우는 위상학적으로 뻔한 절연체, 즉 보통 절연체이다. 조금 더 수학적으로 말하자면, \({\bf R}_{\bf k}\)가 형성하는 고리가 원점을 감싸면 베리 위상Berry phase은 \(\pi\)이고, 감싸지 않으면 베리 위상은 \(0\)이다. 참고로 [그림5]는 이렇게 서로 다른 두 가지 상황을 보여준다.
[그림5]에서 기술된 보통 절연체와 위상 절연체가 위상학적으로 서로 다름을 보여주기 위해서 비유를 하나 들어보자. [그림 6]은 나무판자 중간에 못이 하나 박혀있고, 주변에 고리 모양의 밧줄rope이 떨어져 있는 상황을 보여준다. 위상학적으로 말해서, 밧줄이 떨어져 있는 상황은 2가지 경우 중의 하나로 구분된다. 즉, (1) 밧줄이 못을 둘러싸지 않는, 따라서 위상학적으로 뻔한 경우와 (2) 밧줄이 못을 둘러싸는, 따라서 위상학적으로 뻔하지 않은 경우이다. 이 2가지 경우는 밧줄을 끊거나 아예 못 위로 들어 올리지 않는 한, 아무리 변형해도 서로 연결되지 않는다. [그림6]의 못과 밧줄은 다름 아니라 각각 [그림5]에서 원점을 지나는 \(R_z\)축과 \({\bf R}_{\bf k}\)가 형성하는 고리를 의미한다.
보통 절연체와 위상 절연체는 물리적으로 어떤 차이가 있는 것일까? 기억을 되살려 보면 “믿기 힘든 양자 Incredible Quantum [8]: 위상의 귀환”에서 배우기를 보통 절연체와 위상 절연체의 물리적인 차이는 시스템의 경계, 즉 표면에서 발생한다고 했다. 즉, 보통 절연체에서 전자는 절연체 내부는 물론이고 표면에서도 흐를 수 없다. 반면에 위상 절연체에서 전자는 절연체 내부에서는 흐를 수 없지만 표면에서는 매우 잘 흐를 수 있다.
엄밀하게 말해서, 1과 2차원 시스템의 경계는 표면이 아니라 가장자리, 영어로 에지edge라고 불린다. 따라서 1과 2차원 시스템의 경우에 보통 및 위상 절연체의 차이는 가장자리를 따라서 자유롭게 돌아다닐 수 있는 상태가 있는가 없는가에 따라서 구분된다. 전문적으로 이렇게 가장자리를 따라서 자유롭게 돌아다닐 수 있는 상태를 에지 상태edge state라고 부른다.
특히, 앞서 분석한 1차원 절연체의 경우에 가장자리는 1차원 격자의 양 끝점에 불과하다. 따라서 이 경우에 에지 상태는 양 끝점에 묶인 상태가 된다. 결론적으로 1차원 절연체의 경우에 위상학적으로 뻔한 상황과 뻔하지 않은 상황을 물리적으로 구분해주는 것은 에지 상태의 존재 여부이다.
그런데 에지 상태의 존재 여부는 앞에서 분석한 것처럼 주기적인 경계 조건 하에서 푸리에 변환을 이용하는 방법을 써서는 판단할 수 없다. 주기적인 경계 조건 하에서는 실질적으로 가장자리가 없기 때문이다. 우리는 기본으로 돌아가야 한다.
기본은 1차원 격자 문제를 풀기 위해서 맨 처음에 썼던 방법 그대로 닫힌 경계 조건 하에서 해밀토니안을 직접 행렬로 표현한 다음에 곧이곧대로 대각화하는 것이다. 여기서는 지면 관계 상 이 방법에 대해서 자세하게 기술하지 못 한다. 하지만 실제로 해 보면 앞서 설명한 바와 같이 정확하게 베리 위상이 \(\pi\) 혹은 \(0\)인가에 따라서 에지 상태가 있는지 없는지가 결정된다!
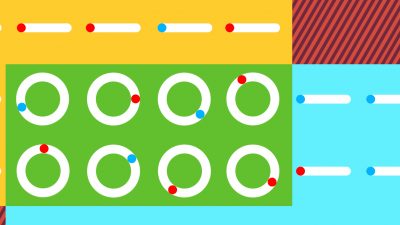
참고로 [그림5]의 아래에 있는 두 그림은 (1) 보통 및 (2) 위상 절연체가 가장자리에서 어떻게 다른지를 묘사한다. 그림에서 타원은 \(A\)와 \(B\)원자가 대략 한 쌍의 묶음으로 생각할 수 있다는 것을 의미한다. 보통 절연체의 경우에는 모든 원자들이 빠짐없이 단위 격자 내에서 쌍을 이룰 수 있다. 반면에 위상 절연체의 경우에는 단위 격자를 넘어서 쌍을 이루기 때문에 가장자리에 있는 원자는 짝이 없이 홀로 존재한다는 것을 알 수 있다. 이렇게 짝이 없이 가장자리에서 대롱대롱 매달려 있는 원자가 바로 에지 상태를 구성한다.
결국, 단순하게 보이는 1차원 격자 위에도 위상 절연체가 존재할 수 있는 것이다.
빛보다 느리지만 상대성 이론: 그래핀
이제 1차원에서 한 차원을 올려서 2차원으로 올라가 보자.
2차원에서 가장 쉬운 격자 구조는 사각 격자square lattice이다. 그런데 이 경우에는 조금만 생각해 보면 \(x\)와 \(y\) 방향은 각각 독립적인 1차원 문제로 귀착된다는 것을 깨달을 수 있다. 그렇다면 에너지 고유값은 단순히 \(x\)와 \(y\) 방향의 에너지 고유값을 더하면 될 것이다. 즉, 에너지와 파수 사이의 분산 관계식은 다음과 같이 주어진다.
\(\epsilon_k=-2t(\cos{k_x}+\cos{k_y})\)
여기서 \(k_x\)와 \(k_y\)는 각각 \(x\)와 \(y\) 방향으로의 파수이다.
조금 싱거우니 약간 더 재미있는 문제를 생각해 보자. 가만히 생각해 보면, 2차원 격자 문제는 2차원 평면을 반복되는 타일로 빠짐없이 덮는 방법을 찾는 것과 동일하다. 어떤 종류의 타일이 필요한지는 소위 군group 이론이라는 수학 이론을 이용해서 엄밀하게 모두 찾을 수 있다. 참고로, 2차원에서는 총 5종류의 격자 구조가 가능하다. 여기서는 이런 엄밀한 방법보다는 직관에 의존하는 분류법을 쓰기로 하자.
편의상 한 가지 종류의 타일로 2차원 평면으로 덮는 경우만 생각해 보자.
변의 개수가 가장 적은 도형은 삼각형이다. 즉, 삼각형 타일로 2차원 평면을 덮는 것이다. 이 경우에 격자는 삼각 격자triangular lattice, 혹은 처음 들으면 조금 헷갈리지만 육방 격자hexagonal lattice라고 불린다. 육방 격자라고 불리는 이유는 삼각 격자의 각 격자점 주변에 6개의 방향으로 최인접nearest-neighbor 격자점이 위치하기 때문이다.
다음 도형은 물론 사각형이다. 정사각형과 직사각형을 포함해서 사각형 타일로 2차원 평면을 덮는다면 사각 격자가 형성된다. 사각 격자 문제는 앞에서 분석해 보았다.
삼각형과 사각형의 다음 도형은 오각형이다. 그런데 조금만 생각해도 알 수 있듯이 오각형으로는 2차원 평면을 빠짐없이 다 덮을 수 없다.
그런데 약간 옆길로 새는 이야기이기는 하지만, 재미있게도 두 종류의 타일이 있다면 2차원 평면을 다섯 방향의 대칭성을 가지는 방식으로 빠짐없이 덮을 수 있다. 이러한 방식으로 타일을 덮는 방법을 “펜로즈 타일링Penrose tiling”이라고 한다. 참고로, [그림7]은 펜로즈 타일링을 보여준다.
사실 펜로즈 타일링이 과학적으로 흥미로운 이유는 격자 구조에 주기성이 없기 때문이다. 이렇게 질서는 있지만 주기성이 전혀 없는 격자 구조를 가지는 결정을 준결정quasicrystal이라고 부른다. 준결정의 존재는 사람들을 매우 놀라게 했다. 준결정은 처음 그것이 실제로 존재할 수 있다고 주장한 대니얼 셰시트먼Daniel Shechtman이 학계에서 잠시 동안 쫓겨날 정도로 학계의 통설에서 크게 벗어나 있었다. 다행히 셰시트먼의 주장은 정밀하게 증명되었고 그는 이 공로로 2011년 노벨 화학상을 받게 된다.
오각형 구조를 가지는 준결정만큼 충격적이지는 않지만, 육각형 타일로 2차원 평면을 덮는 문제도 매우 중요하다. 육각형 타일로 이루어지는 2차원 격자는 벌집 격자honeycomb lattice라고 불린다. 그리고 벌집 격자를 이루는 대표적인 2차원 물질은 바로 그 유명한 그래핀graphene이다. 그래핀은 최근에 가장 큰 각광을 받고 있는 양자물질 중의 하나이다.
그래핀은 탄소 원자들이 벌집 격자 구조를 이루는 2차원 물질이다. 나중에 더 자세하게 논의할 기회가 있겠지만 고체를 구성하는 원자들의 결합 구조는 원자의 가장 바깥을 차지하고 있는 궤도, 즉 최외각 궤도에 의해서 주로 결정된다. 탄소 원자는 최외각 궤도에 4개의 전자가 퍼져 있다. 이것의 결과로 탄소 원자는 마치 4개의 연결 고리가 밖으로 뻗어있는 레고 조각과 같이 행동하게 된다.
구체적으로, 그래핀에서는 4개의 연결 고리 중에서 3개가 2차원 평면에 국한되어 120도를 이루며 펼쳐지게 된다. 이렇게 펼쳐진 3개의 연결 고리는 주변의 탄소 원자에서 나오는 다른 3개의 연결 고리들과 자연스럽게 연결된다. 최종적으로 얻어지는 격자 구조는 벌집 격자이다. 참고로 [그림8]은 그래핀의 벌집 격자 구조를 보여준다.
나머지 1개의 연결 고리는 어떻게 되는 것일까? 나머지 1개의 연결 고리는 2차원 평면을 벗어나 3차원을 향하게 된다. 그 결과 이 연결 고리에 담긴 전자는 2차원 평면에 국한되는 것이 아니라 2차원 평면 위(혹은 아래)를 자유롭게 떠다닐 수 있게 된다.
이제 이렇게 자유롭게 떠다니는 전자는 어떠한 동역학을 가지는지 알아보자. 다시 말해서, 벌집 격자 위에서 자유롭게 돌아다니는 전자의 에너지 고유값, 즉 에너지-파수 분산 관계식을 구해보자. 논의를 간단하게 하기 위해서 자유 전자들은 벌집 격자 위에서 바로 최인접 탄소 원자 사이만 뛰어다닐 수 있다고 가정하자. 이 경우에 그래핀 해밀토니안을 다음과 같이 쓰인다.
\(H= -t \sum_{\langle {\bf r}_i, {\bf r}_j \rangle} \left(c^\dagger_{A,{\bf r}_i}c_{B,{\bf r}_j}+c^\dagger_{B,{\bf r}_j}c_{A,{\bf r}_i}\right)\)
위에서 \(\langle {\bf r}_i, {\bf r}_j \rangle\)은 \({\bf r}_i\)와 \({\bf r}_j\)가 최인접 격자점인 경우에만 합이 취해진다는 것을 의미한다.
위 해밀토니안이 알려주는 중요한 사실이 하나 있다. 그것은 바로 벌집 격자의 격자점은 반드시 두 종류, 즉 \(A\)와 \(B\) 격자점으로 구분되어야 한다는 사실이다. 그 이유는 \(A\)와 \(B\) 격자점이 주변 격자점들과 가지는 연결 구조가 다르기 때문이다. [그림9]을 참조하라.
이렇게 두 종류의 격자점이 필요하다는 사실은 앞서 뜀 계수가 번갈아 바뀌는 1차원 격자 문제와 비슷하다. 앞서 썼던 푸리에 변환 방법을 그래핀 문제에 비슷하게 적용할 수 있다는 의미이다. 구체적으로, 위 해밀토니안은 블로흐 파동의 파수 공간에서 다음과 같이 표현된다.
\(H=\sum_{\bf k}(\begin{array}{cc}c^\dagger_{A,{\bf k}} &c^\dagger_{B,{\bf k}}\end{array})\hat{H}_{\bf k}\left(\begin{array}{c}c_{A,{\bf k}} \\ c_{B,{\bf k}}\end{array}\right)=\sum_{\bf k}(\begin{array}{cc}c^\dagger_{A,{\bf k}} & c^\dagger_{B,{\bf k}}\end{array})\left(\begin{array}{cc}0 & \Delta_{\bf k} \\\Delta^*_{\bf k} & 0\end{array}\right)\left(\begin{array}{c}c_{A,{\bf k}} \\ c_{B,{\bf k}}\end{array}\right)\)
여기서 \(\Delta_{\bf k}\)는 다음과 같이 정의된다.
\(\Delta_{\bf k}=-t (e^{i{\bf k}\cdot{\bf c}_1}+e^{i{\bf k}\cdot{\bf c}_2}+e^{i{\bf k}\cdot{\bf c}_3})\)
위에서 \({\bf c}_1, {\bf c}_2, {\bf c}_3\)은 [그림9]에서 보듯이 주어진 격자점, 예를 들어 어떤 \(A\) 격자점에서 최인접한 \(B\) 격자점들로 연결하는 벡터이다.
앞서 말했듯이 위 해밀토니안은 앞에서 풀어 본 뜀 계수가 번갈아 바뀌는 1차원 해밀토니안과 수학적으로 완벽하게 동일한 형태를 지니고 있다. 따라서 에너지 고유값도 동일한 형태로 얻어진다.
\(\epsilon_{\bf k}=\pm |\Delta_{\bf k}|=\pm t|e^{i{\bf k}\cdot{\bf c}_1}+e^{i{\bf k}\cdot{\bf c}_2}+e^{i{\bf k}\cdot{\bf c}_3}|\)
위 분산 관계식은 사실 제곱근 안에 몇 개의 삼각 함수가 들어가 있는 형태에 불과하기 때문에 아주 복잡하지는 않다. 다만 에너지가 2개의 파수 \(k_x, k_y\)의 함수이기 때문에 실제로 어떻게 생겼는지 알기 위해서 에너지를 3차원 그래프로 그리는 것이 필요하다.
이러한 3차원 그래프는 보통 컴퓨터로 계산해서 그리지만 여기서는 필자가 스케치한 [그림10]로 대체하고자 한다. 3차원 그래프를 그리는 것이 쉽지는 않으나 열심히 노력해서 그려보면 전체적인 모습을 머릿속에 각인시키는 데에 큰 도움이 된다. 독자들도 한번 시도해 보기를 추천한다.
자, [그림10]에서 보면 알 수 있듯이 두 에너지띠는 6개의 점에서 서로 만난다. 특히, 각각 만나는 점에서의 에너지-파수의 분산 관계식은 2개의 원뿔cone이 서로 위아래로 마주 보면서 꼭지점에서 정확히 만나는 모습을 보인다. 전문적으로 이러한 원뿔 구조를 디랙 원뿔Dirac cone이라고 부르고 디랙 원뿔의 꼭지점을 디랙 점Dirac point라고 부른다. [그림10]에서 “풍선” 부분은 꼭지점 부분이 확대된 모습을 보여 준다.
사실, 엄밀하게 말해서 서로 독립적인 디랙 원뿔의 개수는 6개가 아니라 2개이다. 그 이유는 2개의 파수가 가질 수 있는 값들이 2차원 전 평면이 아니라 특정한 영역으로 제한되기 때문이다. 근본적으로 이렇게 되는 이유는 격자점들 사이의 거리가 유한하게 떨어져 있어서 그보다 더 작은 파장을 가지는 파동은 의미가 없기 때문이다. 파장과 파수는 역수의 관계로 연결된다는 사실을 기억하라. 따라서 특정한 범위 내에서의 파수만이 의미가 있고, 그 영역을 넘어서는 파수의 값은 불필요하다. 이렇게 의미 있는 파수 값의 영역을 전문적으로 “브릴루앙 영역Brillouin zone”이라고 한다.
벌집 격자의 경우에 브릴루앙 영역은 실공간의 타일과 비슷하게 육각형의 모습을 지닌다. 그리고 이 육각형의 각 꼭지점들은 바로 앞서 언급한 디랙 원뿔들의 꼭지점과 일치한다. [그림11]은 브릴루앙 영역에서 디랙 원뿔들이 어떻게 위치하고 있는가를 보여 준다. 사실 [그림11]은 [그림10]을 디랙 원뿔의 꼭지점 근처의 좁은 에너지 영역에 집중해서 그린 그림에 불과하다.
처음 보면 그러려니 하겠지만, 사실 여기서 아주 재미있는 일이 발생했다. 디랙 원뿔 근처에서 에너지, 즉 운동 에너지가 파수, 즉 운동량에 선형으로 비례하는 분산 관계식이 나온 것이다. 보통 운동 에너지는 운동량의 제곱에 비례한다. 적어도 뉴턴의 동역학에서는 그렇다. 그런데 그래핀에서 운동 에너지는 운동량의 절대값에 선형으로 비례한다.
\(\epsilon_{\bf k}=\pm v_F \sqrt{k^2_x+k^2_y}\)
여기서 \(v_F\)는 쉽게 말해서 디랙 원뿔의 기울기이다. 이러한 분산 관계식을 만족하는 입자로 우리가 잘 아는 입자는 바로 빛 혹은 광자이다. 그래핀에서 전자는 빛과 같이 질량 없이 상대론적으로 움직일 수 있는 입자가 된 것이다!
물론 전자가 진짜 빛처럼 빠르게 움직일 수 있게 됐다는 뜻은 아니다. \(v_F\)는 실제 광속보다는 엄청나게 느리다. 하지만 동역학에 관한 한 그래핀 내의 전자와 빛은 완벽하게 똑같은 법칙을 따른다. 빛보다 느리지만 상대성 이론이 나타난 것이다!
그래핀과 같이 광속과 전혀 상관없는 것처럼 보이는 응집물질에서 상대성 이론이 나타난 것은 매우 놀랍니다. 하지만 더 놀라운 성질이 아직 우리를 기다리고 있다.
구체적으로, 그래핀에 모종의 섭동을 주어서 디랙 원뿔의 꼭지점 사이를 벌릴 수 있다고 하자. 즉, 에너지 간격을 열 수 있다고 하자. 에너지 간격이 열렸으므로 새로 만들어진 물질은 물론 절연체이다. 그런데 에너지 간격이 열리는 방식에 따라서 위상학적으로 뻔하거나 뻔하지 않은 절연체가 될 수 있다. 다시 위상의 귀환이다!
수학적으로, 에너지 간격은 해밀토니안에 질량 항mass term이 발생하면 열릴 수 있다.
\(\hat{H}_{\bf k}=\left(\begin{array}{cc}m_{\bf k} & \Delta_{\bf k} \\\Delta^*_{\bf k} & -m_{\bf k}\end{array}\right)={\bf R}_{\bf k}\cdot\boldsymbol{\sigma}\)
위에서 \({\bf R}_{\bf k}\)는 다음과 같이 정의된다.
\({\bf R}_{\bf k}=({\rm Re}\Delta_{\bf k},-{\rm Im}\Delta_{\bf k},m_{\bf k})\)
이러한 상황에서 에너지 고유값은 다음과 같이 주어진다.
\(\epsilon_{\bf k}=\pm\sqrt{|\Delta_{\bf k}|^2+m^2_{\bf k}}\)
여기서 자세하게 설명하기는 쉽지 않지만, 질량 항인 \(m_{\bf k}\)는 디랙 원뿔의 꼭지점 근처에서 일반적으로 다음과 같이 전개될 수 있다.
\(m_{\bf k} \simeq M+B(k^2_x+k^2_y)\)
이제 “믿기 힘든 양자 Incredible Quantum [8]: 위상의 귀환”에서 배운 바를 기억해 보자. \({\bf R}_{\bf k}\)가 2차원 파수 \({\bf k}\)의 함수로 “보자기”를 형성한다고 할 때, 이 보자기로 원점에 있는 자기 홀극을 감쌀 수 있으면 위상 절연체가 되고, 그렇지 않으면 보통 절연체가 된다. 위 해밀토니안의 경우에 곰곰이 잘 생각해 보면, 위상 절연체가 되는 조건은 \(MB<0\)이고, 보통 절연체가 되는 조건은 그 반대인 \(MB>0\)이다.
마지막으로, 질량 항은 실제로 어떻게 만들어질 수 있을까? 질량 항을 만드는 데에 딱 한 가지 방법만 있는 것은 아니다. 우선, 가장 처음 제안된 방법은 전체적으로 다 합치면 \(0\)이지만 적절하게 잘 출렁거리는 자기장을 거는 것이다. 이후에 제안된 두 번째 방법은 그래핀에 내재하는 적절한 스핀-궤도 결합spin-orbit coupling을 이용하는 것이다. 참고로, 첫 번째 방법을 제안한 사람은 던컨 할데인Duncan Haldane으로 이 업적을 비롯해서 위상 물질의 발견에 기여한 여러 공로를 인정받아서 2016년 노벨 물리학상을 받았다. 두 번째 방법을 제안한 사람들은 찰스 케인Charles Kane과 유진 멜레Eugene Mele로 스핀-궤도 결합을 이용하는 소위 케인-멜레 모형Kane-Mele model을 개발한 공로로 위상 물질 연구에 중대한 돌파구를 마련했다고 인정받고 있다.
흑연과 다이아몬드
이제 다시 한 번, 2차원에서 한 차원을 높여서 3차원으로 올라가 보자.
3차원의 격자 구조는 2차원에 비해서 매우 복잡해진다. 앞선 섹션에서 언급한 군 이론을 이용해서 3차원에서 가능한 격자 구조를 모두 찾아보면 총 14 종류가 가능하다. 이렇게 서로 다른 종류의 격자 구조를 전문적으로 “브라베 격자Bravais lattice”라고 한다. 14개의 브라베 격자에 대해서 여기서 자세하게 설명할 수는 없다. 현재 우리의 상황에서 유용한 직관을 가져다 주기에는 너무 복잡하기 때문이다. 대신 2차원에 관해서 논의한 것과 비슷하게 간단한 몇 가지 예를 조금 자세히 분석해 보자.
우선, 당연한 말 같지만 3차원은 정육면체 상자로 채울 수 있다. 이러한 격자 구조를 입방 격자cubic lattice라고 부른다. 참고로 [그림12]은 입방 격자 구조를 보여주는 M. C. 에셔의 판화 <Cubic Space Division>이다.
3차원 입방 격자는 2차원 사각 격자와 비슷하게 \(x, y, z\) 방향이 서로 독립적이다. 따라서 에너지-파수 분산 관계식은 3 방향의 에너지 고유값을 그냥 더하면 된다.
\(\epsilon_{\bf k}= -2t (\cos{k_x}+\cos{k_y}+\cos{k_z})\)
위에서 물론 \(k_x, k_y, k_z\)는 각각 \(x, y, z\) 방향으로의 파수이다.
이제 약간 더 재미있는 3차원 격자 구조를 생각해 보자. 구체적으로, 이전 섹션에서 탄소 원자들이 만드는 2차원 격자 구조를 생각해 본 김에 탄소 원자들이 3차원에서는 어떤 격자 구조를 만드는지 생각해 보자.
탄소 원자들이 3차원에서 격자 구조를 만들어서 생기는 물질에는 크게 두 종류의 물질이 있다. 흑연graphite과 다이아몬드diamond가 바로 그것이다. 재미있는 사실은 이 둘은 모두 탄소 원자로 이루어져 있지만 3차원 격자 구조에 따라서 정말 다르게 보인다는 사실이다.
우선, 흑연은 마치 시루떡처럼 그래핀이 층층이 쌓여서 만들어진다. 그래핀 층 사이의 상호작용은 앞선 섹션에서 설명했듯이 자유롭게 움직이는 전자들이 매개하기 때문에 상대적으로 약하다. 여기서 자세하게 설명할 수 없지만, 이런 상황에서 발생하는 상호작용은 분자 사이의 약한 상호작용을 기술하는 반데르발스 상호작용van der Waals interaction이라고 알려져 있다. 반데르발스 상호작용이 약한 것은 흑연의 표면이 쉽사리 벗겨진다는 사실로부터 미루어 알 수 있다. 흑연이 연필심으로 쓰이는 이유이기도 하다. 그리고 그래핀 층 사이를 자유롭게 움직이는 전자들 덕분에 흑연은 전기가 잘 통한다. 즉, 흑연은 좋은 도체이다.
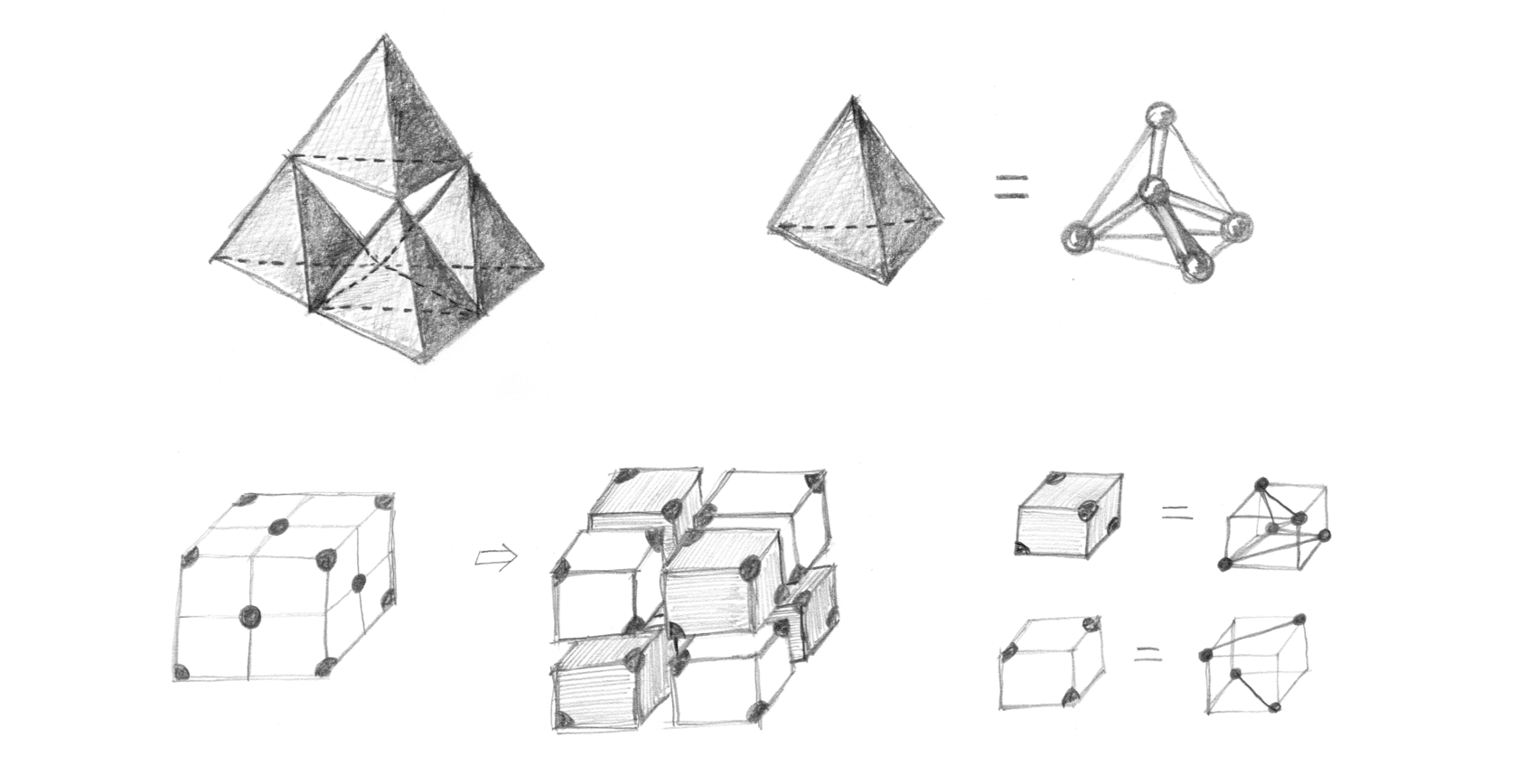
반면에 다이아몬드는 탄소 원자가 갖고 있는 4개의 최외각 전자들이 최대한 3차원적으로 벌어지면서 만들어진다. 즉, 다이아몬드에서 탄소 원자는 정사면체tetrahedron 모양의 레고 블록으로 생각할 수 있다. [그림13]는 이러한 정사면체 레고 블록을 차곡차곡 최대한 빽빽하게 쌓는 방법을 보여 준다. 이것이 바로 다이아몬드 격자 구조이다. 언뜻 보기에도 다이아몬드 격자 구조는 상당히 단단해 보인다. 잘 알고 있듯이 다이아몬드는 세상에서 가장 단단하고 밀도가 높은 물질이다. 참고로 다이아몬드에서는 4개의 최외각 전자들이 모두 격자 구조를 만드는 데에 쓰이기 때문에 자유롭게 돌아다닐 수 있는 전자가 없다. 따라서 다이아몬드는 좋은 절연체이다.
이 즈음에서 처음 들으면 직관에 반하는 비밀을 하나 말해주고자 한다. 다이아몬드 격자 구조는 앞서 이 섹션의 초반에서 언급한 입방 격자 구조의 일종이다! 조금 더 구체적으로 말해서 면심 입방 격자 구조face-centered cubic lattice이다. 여기서 “면심face-centered”이란 입방 격자 구조의 기본 단위인 정육면체가 지니는 각 6개 면의 중심에 격자점이 하나씩 덧붙여져 있다는 의미이다. 이런 관점에서 다이아몬드 격자 구조는 상대적으로 약간 비껴 있는 2개의 면심 입방 격자가 서로 겹쳐있는 구조라고 볼 수 있다. [그림13]은 면심 입방 격자의 관점에서 어떻게 다이아몬드 격자 구조를 이해할 수 있는지를 보여 준다. [그림 13]에서 빗금 쳐진 작은 정육면체는 사실 [그림12]에서 보여준 정사면체 모양의 레고 블록과 같다.
이처럼 똑같은 3차원 격자일지라도 그 구조를 해석하는 방법에는 여러 가지 다른 관점이 있을 수 있다. 어찌 보면 밤하늘의 별을 보면서 그 속에 담긴 모양, 즉 별자리를 상상하는 것과 비슷하다.
자발적 대칭성 붕괴
앞선 논의에서 우리는 각 차원마다 원자들이 규칙적으로 반복되는 질서를 형성해서 만들 수 있는 격자 구조에 대해서 생각해 보았다. 그리고 우리는 몇몇 예를 통해서 전자들이 주어진 격자 구조 위에서 돌아다닐 때 어떠한 에너지-파수 분산 관계식을 가질 수 있는지를 살펴보았다.
그런데 원자들은 어떻게 특정한 질서를 선택하는 것일까? 아무도 개별 원자에게 “너는 이곳에 있고, 너는 저기에 있어라”라고 명령을 내리지 않는다. 원자들이 자발적으로 알아서 자신들에게 걸맞은 격자 구조를 형성하는 것이다.
구체적으로, 앞서 이야기한 흑연과 다이아몬드의 경우에 두 물질 상태를 이루는 원자는 모두 같은 탄소이다. 그런데 탄소는 때에 따라서 흑연을 만들기도 하고 다이아몬드를 만들기도 한다. 흑연과 다이아몬드 중에서 어떤 물질 상태가 선택되는지는 두 가지 중요한 물리량이 결정한다. 바로 온도와 압력이다.
어느 유명한 다이아몬드 회사의 슬로건인 “다이아몬드는 영원하다A Diamond is Forever”와 다르게 상온과 1기압 하에서 다이아몬드는 영원하지 않다. 즉, 다이아몬드는 아주 천천히 흑연으로 변한다. 물론 흑연과 다이아몬드는 탄소의 고체 상태이고, 온도를 더 높이거나 압력을 더 낮추면 탄소는 액체나 기체 상태를 형성할 수 있다.
이렇듯 응집물질, 특히 고체 상태를 이루기 위해서 원자들은 자발적으로 규칙적으로 반복되는 질서를 만들어야 한다. 조금 복잡하게 들리지만 이를 전문적으로 “공간의 병진 대칭성translational symmetry이 자발적으로 붕괴된다”라고 표현한다. 공간의 병진 대칭성이란 실공간의 주어진 방향으로 앞뒤로 움직일 때 물리량에 아무런 차이가 없다는 것을 의미한다. 실제로 우리가 아는 한 원자들은 실공간에서 아무 위치나 차지할 수 있다. 하지만 고체 내에서 원자들은 규칙적으로 반복되는 위치, 즉 격자점에만 위치할 수 있다.
정리하면 다음과 같다. 온도나 압력과 같은 외부 조절 변수가 주어지면 어느 정도의 격자 간격을 가지고 어떠한 격자 구조를 가지는 고체 상태가 형성되어야 하는지가 내재적으로 결정된다. 하지만 실제로 그러한 고체 상태가 실현되기 위해서는 공간의 병진 대칭성이 자발적으로 붕괴되어야 한다.
자발적 대칭성 붕괴spontaneous symmetry breaking는 물리에서 가장 심오한 원리 중의 하나이다. 나중에 보겠지만 이 원리는 우리 우주의 운명, 그리고 우리 자신의 존재를 규정짓는다.