Think different. -Steve Jobs
More is different. -Philip W. Anderson
Think more to think different. -KP
실험 철학experimental philosophy이라는 학문이 있다. 언뜻 “실험”과 “철학”이 하나의 단어로 묶여서 조금 생뚱맞게 느껴지는 실험 철학이란 도대체 어떤 학문일까?
거칠게 말해서, 실험 철학이란 어떤 주어진 철학 문제를 해결하기 위해서 전문 철학자가 아닌 일반 사람들을 상대로 설문을 수행하고, 그 결과를 통계적으로 분석하여 해당 문제에 관한 직관을 얻고자 하는 학문이다. 실험 철학은 최근에 철학에서 가장 각광을 받고 있는 분야 중의 하나라고 하는데, 그러한 지위에 오르게 된 데에는 한 문제가 중요한 역할을 했다.
문제는 다음과 같다.
“자유의지free will는 과연 존재하는가?”
조금 다르게 표현하면 다음과 같다.
“자유의지와 결정론determinism은 과연 양립가능한가?”
결정론이란 간단하게 말해서 우주에서 벌어지는 모든 사건은 반드시 그것을 일으키는 원인이 있으며, 결과는 원인에 의해서 완벽하게 결정된다는 이론이다. 특히 과학적인 의미에서 결정론은 우주에서 벌어지는 모든 사건은 그 이전 어느 시점에 일어난 사건들의 정보, 소위 초기 조건initial condition과 사건들 사이의 인과관계를 기술하는 물리법칙에 의해서 완벽하게 결정된다는 것을 의미한다. 궁극적으로 결정론에 따르면 우주의 모든 사건은 이미 결정되어 있다.
그렇다면 혹시 자유의지는 단지 우리의 착각에 불과한 것이 아닌가? 이와 관련해서 17세기 네덜란드 철학자인 스피노자는 다음과 같이 말했다.
“사람들이 자신이 자유롭다고 믿는 것은 실수이다. 그것은 단지 사람들이 자신의 행동은 인지하지만, 그것을 결정한 원인에 대해서는 무지하기 때문이다.”
“Men are mistaken in what they believe themselves free in their opinion is simply because they are aware of their actions, and ignorant of the causes that determine them.”
자유의지와 결정론의 문제는 단순히 이론적인 문제가 아니다. 왜냐하면 만약 자유의지가 정말 없다면 우리는 궁극적으로 우리의 행동에 대해서 아무런 도덕적인 책임을 질 필요가 없기 때문이다. 조금 과장해서 말하면, 죄를 지은 그 어떤 사람에게도 벌을 내릴 수 없다. 죄를 지은 사람에게 다른 선택지가 없었기 때문이다. 어찌 보면 죄라는 것 자체가 존재하지 않는다.
과연 그럴까?
구체적으로 실험 철학은 자유의지와 결정론 문제에 관하여 다음과 같은 세 가지 상황을 고려해 볼 것을 제안한다.
(1) 완벽하게 결정론적으로 작동하는 가공의 우주에 A가 살고 있다. A는 어느 날 B를 죽이게 되었다. A는 도덕적인 책임이 있는가?
(2) 남편에게 싫증이 난 에이미는 남편을 죽이기 위해서 치밀한 계획을 세운다. 구체적으로, 에이미는 직접 남편을 죽이는 대신 자신이 실종된 것처럼 꾸미려고 한다. 이는 남편이 부인인 자신을 살인하고 유기했다는 누명을 씌우기 위함이다. 계획이 잘 실행된다면 남편은 살인죄로 처형을 당하게 될 것이다. 에이미는 자신의 행동에 도덕적인 책임이 있는가?
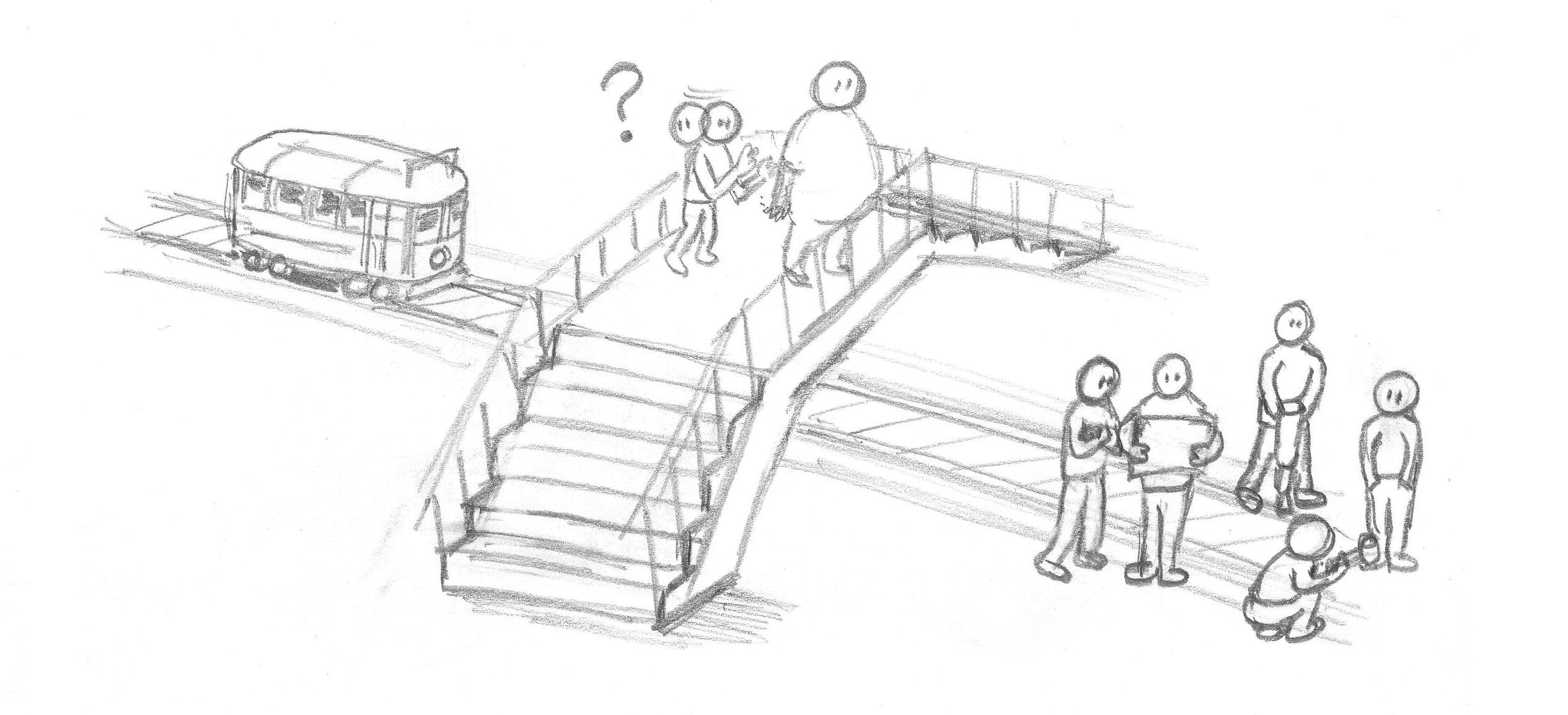
(3) 나는 육교 위에서 언덕을 내려오는 트롤리trolley 기차를 바라보고 있다. 그런데 갑자기 트롤리 기차의 브레이크에 고장이 났다. 그대로 두면 언덕 아래 기차 선로 위에서 일하고 있는 5명의 인부들은 트롤리 기차에 치어 죽게 될 것이다. 트롤리 기차를 막을 수 있는 방법은 무엇인가 무거운 물체를 선로 위로 떨어뜨리는 것이다. 마침 내 앞에는 뚱뚱한 사람이 한 명 서 있다. 만약 내가 그 사람을 밀어 떨어뜨린다면 1명을 희생시키는 대신에 5명을 구할 수 있다. 참고로 아래 [그림1-1]을 보라. 하지만 고민 끝에 나는 가만히 있기로 한다. 나는 다섯 인부의 죽음에 도덕적인 책임이 있는가?
우선 아마도 거의 모든 사람들은 (1)번 상황의 A는 아무런 도덕적인 책임이 없다고 생각할 것이다. 반면에 대부분의 사람들은 (2)번 상황의 에이미는 도덕적인 책임이 있을 뿐만 아니라 법적인 처벌을 받아야 한다고 생각할 것이다. (참고로 (2)번 상황은 영화 <나를 찾아줘Gone Girl>의 줄거리이다.)
그런데 (3)번은 상황이 조금 복잡하다. 일단 현재 (3)번 상황이 기술된 내용만 가지고 보면 상당수의 사람들이 “나”는 도덕적인 책임이 없다고 생각할 것이다. 그런데 여기서 내용을 약간 바꾸어 보면 상황이 180도 달라진다. 예를 들어서 내 앞에 서 있는 뚱뚱한 사람이 사실은 자살하기 위해서 육교에 올라왔으며 이미 난간 위에 올라가 있다고 가정해 보자. 만약 내가 말리지 않는다면 그는 뛰어내릴 것이다. 나는 그를 말려야 하는가 아니면 그대로 두어서 5명의 인부들을 구해야 하는가? 모르기는 몰라도 독자들 중에서 이제 1명을 희생시켜서 5명을 구하는 선택을 한 사람들의 비율이 꽤 높아졌을 것이다. 왜 이렇게 상황이 바뀌게 되는 것일까?
실험 철학을 통해서 밝혀진 바에 따르면, 사람들은 순수하게 추상적인 상황에서는 결정론을 쉽게 받아들인다고 한다. 이 경우에는 자유의지가 없다고 해도 별 문제가 없다. 하지만 구체적으로 현실적인 상황이 복잡하게 덧붙여지면 사람들은 자유의지가 있으며 나쁜 행동을 한 사람은 벌을 받아야 한다고 생각한다고 한다. 즉, 사람들은 원칙적으로는 결정론이 맞지만, 복잡한 현실적인 상황에서는 자유의지가 있다고 믿는 것이다.
이 관점에서 (3)번 상황을 다시 한번 고려해 보자. 처음에 기술된 (3)번 상황과 나중에 바뀐 (3)번 상황은 기본적으로 유사하지만 매우 중요한 점에서 다르다. 바로 화자인 “내”가 의도적으로 잔인한 행동을 해야 하는지 아닌지가 다르다. 의도적으로 잔인한 행동을 하지 않는 것의 대안은 무엇인가? 아무런 행동을 하지 않는 것이다. 아무런 행동을 하지 않으면 어떤 일이 벌어지는가? 처음에 기술된 상황에서 트롤리 기차는 그대로 물리법칙에 따라서 운동할 것이고, 나중에 바뀐 상황에서 뚱뚱한 사람은 예정대로 선로 위로 뛰어내릴 것이다. 도덕적인 딜레마에 빠질 때 우리는 자유의지가 존재하지 않는 결정론적인 우주로 가고 싶다. 그렇게 되면 도덕적인 책임으로부터 자유로울 수 있기 때문이다.
참고로 (3)번 상황은 윤리학과 심리학에서 소위 “트롤리 문제trolley problem”라고 불리는 매우 유명한 문제이다. 트롤리 문제는 자세한 세부 내용에 따라서 다양한 버전을 가지고 있다.
그림1-2 트롤리 문제 / BBC Radio 4
본 논의로 돌아가서, 실험 철학에 따르면 대부분의 사람들은 직관적으로 자유의지와 결정론이 양립가능하다고 믿는다. 물론 그 둘이 정확히 어떻게 양립가능한지를 밝히는 것은 매우 어려운 문제이다. 참고로 이렇게 자유의지와 결정론이 양립가능하다는 입장을 “양립가능론compatibilism”이라고 부른다.
일반 사람들의 직관은 그렇다 치고, 결정론에 바탕을 둔 물리학의 입장에서 자유의지와 결정론은 정말 양립가능할 수 있을까?
이어지는 섹션에서는 물리학의 입장에서 자유의지와 결정론이 정말 양립가능한지 알아보고자 한다. 그러기 위해서는 무엇보다 먼저 결정론이 생각보다 완벽하지 않다는 사실부터 짚고 넘어가야 한다.
카오스와 코펜하겐 해석
뉴턴 역학의 성공으로 결정론은 과학적인 사고방식을 뒷받침하는 철학으로 굳건히 자리매김하였다.
하지만 시간이 흐르면서 완벽한 의미에서의 결정론은 두 가지 큰 문제를 직면한다. 하나는 고전역학의 카오스chaos 현상이고, 다른 하나는 양자역학의 코펜하겐 해석Copenhagen interpretation이다.
첫 번째 문제인 카오스 현상에 대해서 이야기해 보자. 카오스 현상이란 간단하게 말해서 혼돈 현상이다. 조금 더 구체적으로 카오스 상태에 있는, 즉 혼돈에 빠진 입자는 아무리 많은 시간이 흘러도 닫힌 궤도를 형성하지 못하고 무작위로 공간을 휘젓고 다닌다. 앞선 “믿기 힘든 양자 Incredible Quantum [11]: 양자 물질 상태”에서 언급한 바와 같이 카오스 현상의 단초는 3체 문제three-body problem에서 발견되었다. 여기서 3체 문제란 구체적으로 태양-지구-달과 같이 3개의 천체가 중력으로 서로 작용하는 문제이다.
3체 문제가 카오스 현상을 보인다는 사실을 처음 인지한 사람은 앙리 푸앵카레Henri Poincare였다. 1880년대 푸앵카레는 3체 문제의 해 중에서 발산하지 않으면서도 전혀 주기성을 지니지 않는 궤도가 있다는 사실을 발견한다. 이 해는 초기에는 규칙적인 것으로 보이지만, 충분한 시간이 흐른 뒤에는 에너지 보존 법칙이 허용하는 범위 내에서 입자의 위치와 속도로 이루어진 위상 공간의 모든 점을 아무런 패턴 없이 무작위로 모두 훑고 지나가는 성질을 보인다. 바로 카오스 현상이다.
카오스 현상의 가장 중요한 특징은 입자의 동역학이 초기 조건에 극도로 민감하다는 것이다. 초기 조건에 대한 극도의 민감성은 흔히 나비 효과butterfly effect라는 별명으로 불린다. 이 표현은 미국의 기상학자 에드워드 로렌즈Edward Lorenz가 1972년 제139회 미국과학진흥협회American Association for the Advancement of Science에서 수행한 한 강연의 제목인 “브라질에 있는 나비 한 마리의 날개짓이 텍사스에 돌풍을 일으키는가?Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas?”에서 유래했다고 알려져 있다.
다시 말해서 카오스 상태에서 초기 조건에 내재하는 약간의 오류는, 처음에는 아무리 작은 것일지라도 어느 정도 시간이 흐르고 나면 기하급수적으로 증폭되어, 종국에는 입자의 동역학을 정확하게 예측하는 것을 실질적으로 불가능하게 만든다는 것이다. 전문적으로 이렇게 오류가 증폭되는 데에 걸리는 시간을 리야푸노브 시간Lyapunov time이라고 부른다. 여기서 주목해야 할 사실은 입자의 동역학은 여전히 뉴턴의 운동 방정식이라는 완벽하게 결정론적인 방정식에 의해서 기술된다는 것이다. 하지만 그럼에도 불구하고 카오스에 빠진 입자의 동역학을 정확하게 예측하는 것은 실질적으로 불가능하다. 다시 말해서 완벽한 의미에서의 결정론은 실제로 존재하지 않는다.
이제, 두 번째 문제인 양자역학의 코펜하겐 해석에 대해서 이야기해 보자. 코펜하겐 해석은 앞선 여러 글들에서 언급되었지만, 특히 “믿기 힘든 양자 Incredible Quantum [7]: 두 상태 이야기”와 “믿기 힘든 양자 Incredible Quantum [9]: 양자 얽힘”에서 나름 심도 있게 설명했다. 코펜하겐 핵심은 측정에 따른 파동 함수의 붕괴이다.
즉, 코펜하겐 해석에 따르면 주어진 물리량을 측정하는 순간, 파동 함수는 측정하는 물리량에 의해서 규정되는 여러 상태 중의 하나로 붕괴한다. 이때 각 상태로 붕괴할 확률은 파동 함수를 그 상태로 분해했을 때 주어지는 진폭의 절대값의 제곱으로 주어진다. 앞선 카오스 현상의 경우와 조금 결이 다르긴 하지만, 이 경우에도 완벽한 의미에서의 결정론은 실제로 존재하지 않는다.
물론 “믿기 힘든 양자 Incredible Quantum [3]: 파동 방정식”에서 언급했듯이 파동 함수 자체는 여전히 완벽하게 결정론적으로 작동한다. 즉, 파동 함수는 슈뢰딩거 방정식에 의하여 완벽하게 인과적으로 결정된다. 따라서 파동 함수만 놓고 보면 결정론이 맞다. 하지만 물리적으로 의미있는 측정을 하는 순간, 파동 함수는 언제나 확률로 변환되며 결정론의 완벽성은 “희석”된다.
그렇다면 결국 카오스와 코펜하겐 해석은 결정론을 무력화시키고 자유의지를 구원하는가?
아니, 그렇지 않다. 그렇지 않을 뿐만 아니라 어찌 보면 심지어 상황을 더 악화시킨다고 볼 수 있다. 왜냐하면 카오스와 코펜하겐 해석은 자유의지의 존재를 논의하기도 전에 자유의지를 포함한 이 우주의 모든 것이 아예 존재하지 못하게 할 수 있기 때문이다.
열역학 제2법칙
카오스와 코펜하겐 해석은 궁극적으로 우주의 모든 것을 사라지게 할 수 있다.
그 이유는 열역학 제2법칙이라는 물리 법칙 때문이다. 간단하게 말해서 열역학 제2법칙이란 시간 흐름에 방향성이 있음을 말해주는 물리 법칙이다. 조금 더 구체적으로 말해서 열역학 제2법칙에 따르면 엔트로피entropy는 시간에 따라서 절대 감소하지 않는다. 당연한 말 같지만 무엇이 감소하지 않는다는 것은 증가하거나 최소한 고정된다는 것이다. 엔트로피가 정확히 고정되는 경우는 매우 이상적인 상황에서만 가능하기 때문에 대부분의 경우에 엔트로피는 시간에 따라서 증가한다.
그렇다면 엔트로피란 무엇인가? 거칠게 말해서 엔트로피는 무질서도degree of disorder이다. 열역학 제2법칙은 시간이 갈수록 무질서도가 증가한다는 것을 말해준다. 어찌 보면 너무나도 당연한 말이다. 흔히 드는 예를 들자면 깨진 유리병은 다시 원 상태로 조립되지 않으며 모든 생명은 다시 젊어지지 않는다.
열역학 제2법칙은 직관적으로 매우 자명해 보인다. 우리 모두는 유리병이 깨지는 동영상을 되감아서 거꾸로 보여 주면 단박에 이상하다는 사실을 알아차릴 수 있다. 그런데 미시적인 물리 법칙의 관점에서 보면 이야기가 다르다.
네 가지 근본적인 힘 중의 하나인 약력weak force이 작용하는 매우 특별한 경우를 제외하고 거의 모든 미시적인 물리 법칙은 시간 흐름에 대칭성이 있다. 다시 말해서 미시적인 세계에서는 시간 흐름에 방향성이 없다. 참고로 이러한 성질을 “시간 역전 대칭성time-reversal symmetry”이라고 부른다. 방금 전 위에서 든 예를 통해서 말하자면 미시적인 세계에서는 입자들이 움직이는 동영상을 되감아서 거꾸로 보여 주더라도 우리는 그 차이를 전혀 알아차릴 수 없다.
혹시 독자들 중에 약력이 시간 흐름에 방향성을 부여하는 것은 아닌가라고 의심하는 사람이 있을지 모르겠다. 물론 모종의 심오한 이유에 의해서 그렇게 될 수도 있다. 하지만 현재 우리가 알고 있는 한 거시적인 의미에서 시간 흐름에 방향성이 있는 이유는 어떤 특정한 미시적인 물리 법칙이 시간의 대칭성을 깨기 때문이 아니다.
결론부터 이야기하자면 미시 세계에 없던 시간 흐름의 방향성이 거시 세계에서 “저절로” 생겨야 한다.
어떻게 그럴 수 있을까?
뉴턴의 운동 방정식과 슈뢰딩거 방정식으로 대표되는 미시적인 물리 법칙은 모두 미분 방정식의 형태로 주어진다. 앞선 “믿기 힘든 양자 Incredible Quantum [3]: 파동 방정식”에서 이야기했듯이 이것은 모든 임의의 시점의 상태는 바로 그 직전 상태에 의해서 완벽하게 결정된다는 것을 의미한다. 그리고 이것은 어떤 주어진 순간은 그 이전 순간에, 그 이전 순간은 그보다 더 이전 순간의 상태에 의해서 결정된다는 것을 의미한다. 이렇게 만들어진 인과 관계의 사슬은 과거로 쭉 이어져 결국 초기 상태에 도달한다.
거꾸로 말하면 초기 상태에 관한 정보, 즉 초기 조건initial condition이 주어지면 그 이후 모든 순간의 동역학은 완벽하게 인과론적으로 결정된다. 그리고 이러한 인과 관계의 사슬은 미시적인 물리 법칙의 성질에 의해서 시간 역전 대칭성을 지니고 있다. 즉, 인과 관계의 사슬에서는 앞으로 나아가거나 뒤로 거슬러 올라가거나 아무런 차이가 없다. 다만 초기 조건을 정의하는 앞과 뒤가 바뀌는 것이다.
열역학 제2법칙이 맞기 위해서는 인과 관계의 사슬이 끊어져야 한다. 아니, 인과 관계의 사슬이 끊어진다기 보다는 초기 조건의 영향이 사라진다는 표현이 조금 더 정확하다. 이렇게 초기 조건의 영향이 사라지는 방향이 바로 시간이 흐르는 방향인 것이다.
그런데 이 이야기, 어디선가 들어보지 않았나?
앞서 말하기를 시스템이 카오스 상태에 빠지면 아무리 작더라도 초기 조건에 내재하는 오류는 일정 시간(리야푸노브 시간)이 흐른 후에 완전히 증폭되며, 그 결과 입자의 동역학을 정확하게 예측하는 것은 실질적으로 불가능하다고 했다. 다른 말로 하면 카오스 상태에 빠진 시스템은 일정 시간이 흐르고 나면 초기 조건을 완전히 잊어버리고, 에너지 보존 법칙이 허용하는 한에서 접근 가능한 모든 상태들을 무작위로 헤집고 다닌다. 참고로 이러한 성질을 전문적으로 “에르고딕ergodic”이라고 부른다.
만약 위에서 설명한 대로 시스템이 에르고딕하다면, 접근 가능한 모든 상태는 모두 동등한 확률로 나타날 것이다. 그리고 그렇다면 시스템의 무질서도는 최대가 될 것이다. 다시 한번 말하지만 엔트로피는 무질서도이다. 따라서 시스템이 카오스 상태에 빠지면 엔트로피는 자연스럽게 최대가 된다. 이것은 다름 아니라 바로 열역학 제2법칙이다.
이제 열역학 제2법칙을 조금 더 구체적으로 논의하기 위해서 엔트로피를 엄밀하게 정의해 보자. 엔트로피 \(S\)는 수학적으로 다음과 같이 정의된다.
\(S=k_B \ln{\Omega}\)
여기서 \(\ln\)은 자연 로그natural log를 의미하고, \(\Omega\)는 에너지 보존 법칙이 허용하는 한에서 시스템에서 발생할 수 있는 모든 미시 상태microscopic state의 개수를 나타낸다.
위 엔트로피의 정의를 처음 생각한 사람은 루트비히 볼츠만Ludwig Boltzmann이다. 사실 볼츠만 이전에도 엔트로피의 정의는 존재했다. 거칠게 말해서 엔트로피는 열 에너지를 온도로 나눈 값이다. 문제는 열 에너지라는 개념이 미시적으로 잘 정의되지 않는다는 것이다. 물론 볼츠만을 제외한 당대 대다수의 물리학자들은 이 문제에 대해서 크게 신경 쓰지 않았다. 그들에게는 엔트로피가 에너지와 비슷하지만 성질이 묘하게 다른 모종의 거시적인 물리량인 것만으로 충분했다.
하지만 볼츠만은 달랐다. 왜냐하면 볼츠만은 원자론을 굳게 믿고 있었기 때문이다. 이에 볼츠만은 엔트로피가 미시 상태의 성질과 연관되는 모종의 물리량으로 표현되어야 한다고 생각했다. 볼츠만의 이러한 생각의 결과가 바로 앞서 언급한 엔트로피의 정의이다.
구체적으로 볼츠만이 생각하기에 엔트로피가 최대화되는 이유는 (특별한 제한 조건이 있지 않는 한) 모든 미시 상태가 동일한 확률로 나타나야 하기 때문이다.
예를 들어서 초기에 시스템의 동역학에 어떤 특별한 제한 조건이 가해졌다고 하자. 그리고 이것으로 인해서 발생 가능한 총 미시 상태들 중에서 일부만 실제로 발생할 수 있다고 하자. 우화적으로 표현하면 시스템은 평상시에 미시 상태들로 이루어진 가상 공간을 자유롭게 돌아다닐 수 있는데, 갑자기 “제한 조건”이라는 칸막이가 쳐지면서 가상 공간의 일부만 돌아다닐 수 있게 된 것이다. 자, 이제 어느 순간 이 칸막이가 사라진다고 하자. 만약 모든 미시 상태가 동일한 확률로 나타난다면, 시스템은 시간이 흐르면서 점점 더 많은 미시 상태들 사이를 돌아다니게 될 것이다.
이것은 마치 방의 한구석에서 몰래 방귀를 뀌면 시간이 흐르면서 냄새가 방 전체로 퍼지는 것과 같다. 전문적으로 이러한 현상을 확산diffusion이라고 한다. 다름 아니라 이렇게 시간이 흐르면서 실제로 돌아다닐 수 있는 미시 상태의 개수가 점점 늘어나는 원리가 바로 엔트로피 증가의 법칙, 즉 열역학 제2법칙인 것이다.
앞선 볼츠만의 엔트로피 공식은 이러한 열역학 제2법칙을 정확하게 담아내며, 열역학thermodynamics에서 통계 역학statistical mechanics이라는 새로운 물리 분야가 탄생하는 데에 결정적인 역할을 했다.
그런데 여기서 생기는 질문 하나. 열역학 제2법칙은 꼭 카오스 현상을 통해서만 발생할 수 있는가?
카오스로 열역학 제2법칙을 설명하는 데에는 사실 매우 중요한 문제가 존재한다. 그것은 카오스가 순전히 고전역학적인 현상이라는 사실이다. 다시 말해서 카오스는 양자역학적으로는 존재하지 않는다.
양자역학적으로 카오스가 존재하지 않는 이유를 여기서 자세하게 설명할 수는 없다. 다만 최대한 직관적으로 설명하자면, 그 이유는 양자역학이 근본적으로 카오스에서 요구되는 초기 조건에 대한 민감성을 가질 수 없기 때문이다. 쉽게 말해서 양자역학에서는 하이젠베르크의 불확정 원리에 따라서 입자의 위치와 운동량을 애초부터 동시에 정확하게 확정할 수 없다. 그렇다면 초기 조건에 대한 민감성을 논의하는 것 자체가 의미 없어진다.
(재미있게도 양자 카오스quantum chaos라는 용어가 존재하기는 한다. 하지만 위에서 설명했듯이 양자 카오스는 엄밀하게 정의되는 개념이 아니다.)
그렇다면 열역학 제2법칙은 양자역학적으로도 성립하는 법칙인가? 우리는 당연히 그렇다고 생각하고, 실제로 지금까지 수행된 모든 실험 결과로 볼 때도 그렇다.
그럼 열역학 제2법칙은 과연 양자역학에서 어떻게 발생할 수 있는 것일까?
사실 이 질문은 현재 매우 활발하게 연구가 진행되고 있는 주제 중의 하나이다. 여러 다양한 관점들이 있지만, 필자는 그중에서 최근에 가장 크게 각광을 받고 있는 가설 하나에 대해서만 짧게 언급하고자 한다. 이 가설의 이름은 “고유상태 열화 가설eigenstate thermalization hypothesis, ETH”이다. 아래에서는 이 가설을 편의상 ETH로 짧게 줄여서 부르기로 하자.
ETH는 에너지 고유 상태의 물리량을 측정하는 것으로부터 출발한다. 구체적으로 ETH는 어떠한 임의의 고유 상태일지라도 특정한 물리량을 긴 시간에 걸쳐서 측정을 한다면 그 결과가 결국 열적 평형thermal equilibrium 상태가 주는 결과와 정확히 일치한다는 가설이다. 즉, ETH에 따르면 임의의 에너지 고유상태는 그 자체로 언제나 열적 평형에 도달한다. 놀랍게도 이 마법과도 같은 이야기는 실제로 다양한 양자 시스템들을 정확한 대각화exact diagonalization라는 방법을 써서 분석해 보면 매우 잘 맞는다고 알려져 있다.
물론 ETH도 문제를 가지고 있다. 특히 중요한 문제는 “이 가설이 얼마나 일반적으로 맞는가”이다. 이 문제에 대해서는 현재 활발하게 연구가 진행되고 있다. (이 문제의 해결에 관해서 한 가지 아이디어를 언급하자면, 고전역학적으로 카오스를 보이는 시스템을 양자역학적인 시스템으로 변환하면 ETH가 만족될 것이라는 추측이 있다.)
정리해 보자. 아직 100% 완벽하지는 않지만, 열역학 제2법칙은 고전역학적으로 보면 카오스, 양자역학적으로 보면 ETH에 의해서 유도될 수 있다.
여기서 재미있는 관찰 결과 하나.
앞서 언급된 바와 같이 결정론을 무력화시킬 수 있는 두 가지 요소는 고전역학의 카오스와 양자역학의 코펜하겐 해석이다. 알고 있듯이 양자역학에서 측정의 문제는 코펜하겐 해석과 깊은 관련이 있고, ETH는 양자역학적인 측정에 기반한다. 결국 ETH는 코펜하겐 해석과 연결되어 있다고 할 수 있다. 그렇다면 결정론을 무력화시키는 두 가지 요소인 카오스와 코펜하겐 해석은 둘 다 열역학 제2법칙을 발생시키는 데에 중요한 역할을 하는 요소이기도 한 것이다. 결론적으로 카오스와 코펜하겐 해석은 결정론을 무력화시키는 대신에 우리로 하여금 열역학 제2법칙을 맞닥뜨리게 한다.
그런데 이럴 수가? 열역학 제2법칙은 결정론보다 더 큰 문제를 야기한다. 장기적으로 볼 때, 우리 인간은 물론이고 우주의 모든 것은 결국 존재할 수 없기 때문이다.
구체적으로 말해서, 우주의 모든 것은 시간이 흐르면서 무질서도가 최대화되는 상태로 진화한다. 그리고 무질서도가 최대화되는 상태란 다름 아니라 물질을 형성하고 있는 모든 기본 입자들이 다 뿔뿔이 흩어져서 전 우주 공간을 균질하게 채우게 되는 상태, 그야말로 모든 존재가 사라지는 상태이다. 이러한 상태에서는 물론 자유의지도 존재할 수 없다.
그렇다면 우주는, 인간은, 그리고 자유의지는 어떻게 구원될 것인가?
자발적 대칭성 붕괴
열역학 제2법칙과 현재 우리가 아는 우주가 존재한다는 사실을 화해시키는 데에는 사실 아주 쉬운 해결책이 하나 있다.
그 해결책은 바로 현재 우리 우주가 아직 엔트로피가 최대화되어 가고 있는 과정 중에 있는 것이다. 즉, 엔트로피는 우리 우주가 처음 빅뱅big bang을 통해서 탄생할 때 아주 작은 값에서 출발했으며, 현재 증가하고 있는 도중에 있을 뿐이다.
하지만 이 해결책에 따르면 빅뱅 이후에 새로운 질서가 생기는 것을 설명하기가 쉽지 않다. 간단하게 생각하면, 질서는 오로지 깨질 수만 있지 회복될 수 없다. 하지만 우리는 빅뱅 이후로 다양한 종류의 새로운 질서가 생겨왔다는 것을 알고 있다. 예를 들어서, 처음 빅뱅에서 생성된 입자들은 전자, 양성자, 중성자와 같은 아주 기본적인 입자들이다. 이러한 기본 입자들은 처음부터 제대로 된 원자를 구성할 수 없다. 하지만 어떤 이유 때문에 현재 우리가 아는 우주에는 기본 입자들이 뭉쳐서 구성된 다양한 원자들과 원자들로 이루어진 무궁무진한 물질, 그러한 물질들이 고도로 조직화되어 탄생한 생명, 그리고 더 나아가 의식을 지닌 생명이 가지는 자유의지가 존재한다.
새로운 질서는 어떻게 발생할 수 있는 것일까?
우선, 가장 먼저 원자는 어떻게 구성되는가? 원자가 구성되는 원리는 “믿기 힘든 양자 Incredible Quantum [11]: 양자 물질 상태”에서 배웠다. 간단하게 말해서, 전자와 원자핵은 그들을 서로 잡아당기게 하는 전자기력, 즉 쿨롱 상호작용Coulomb interaction으로 인해서 원자를 구성할 수 있다.
그런데 만약 그렇다면 전자와 원자핵은 결국 딱 달라붙어버리지 않을까? 다시 말해서, 원자라는 것은 결국 전자가 원자핵 속으로 빨려 들어감으로써 소멸되지 않을까? 이것은 매우 큰 문제이다. 원자가 없다면 아무런 물질도 존재할 수 없기 때문이다.
다행히 원자는 그렇게 쉽게 소멸되지 않는다. 바로 양자역학이 원자를 지켜주기 때문이다. 다시 말해서 “믿기 힘든 양자 Incredible Quantum [11]: 양자 물질 상태”에서 배웠듯이, 전자는 원자핵 주변에서 안정된 정상파를 형성해야 한다. 전자가 원자핵 속으로 빨려 들어가는 상태는 안정된 정상파가 아니다.
다음으로, 고체가 형성되는 원리는 “믿기 힘든 양자 Incredible Quantum [10]: 더 높은 차원으로”와 “믿기 힘든 양자 Incredible Quantum [11]: 양자 물질 상태”에 걸쳐서 배웠다. 간단하게 말해서, 앞서 양자역학에 의해서 구성된 원자들은 서로 결합하여 자발적으로 자유 공간free space에 규칙적인 구조를 가지고 배열되는 물질 상태, 즉 고체를 형성할 수 있다. 전문적인 용어로, 아무런 질서가 없던 상황에서 자발적으로 질서가 생기는 것을 “자발적 대칭성 붕괴spontaneous symmetry breaking”라고 부른다.
처음 들으면 이상하게 들릴지 모르겠지만, 질서의 발생과 대칭성의 붕괴는 같은 말이다. 구체적으로, 자유 공간의 어느 한 위치와 또 다른 위치는 특별한 이유가 있지 않는 한 아무런 차이가 없어야 한다. 비유적으로 말해서, 지구 위에서 성립하는 물리 법칙은 우주 어디서라도 동일하게 성립해야만 한다. 만약 그렇다면 원자들은 자유 공간에서 어디든지 무작위적으로 동일한 확률로 존재할 수 있어야 한다. 액체나 고체 속 원자들의 위치는 정말 무작위적이다. 이렇게 자유 공간 속 모든 위치가 동등하다는 것은 모종의 대칭성이 있다는 것이고, 전문적으로 이를 병진 대칭성translational symmetry이라고 부른다.
하지만 고체 속 원자들은 이러한 자유 공간의 병진 대칭성을 깬다. 어찌 보면, 이후 발생하는 모든 새로운 질서는 이러한 병진 대칭성의 자발적 붕괴로부터 시작된다고 볼 수 있다.
그렇다면 고체는 정말 구체적으로 어떻게 형성되는가? 우선, 고체가 형성되기 위해서는 모종의 “접착제”가 필요하다. “믿기 힘든 양자 Incredible Quantum [11]: 양자 물질 상태”에서 배웠듯이 접착제는 다름 아니라 원자를 구성하는 바로 그 전자들 중의 일부이다. 조금 더 구체적으로 말해서, 원자를 구성하는 전자들 중의 일부는 원자의 구조를 어느 정도 유지하고, 다른 일부는 원자 밖으로 흘러나와서 원자들을 묶어주는 역할을 하게 된다.
자, 이제 그럼 생명체는 어떻게 탄생하는가?
앞서 설명한 방식에 의해서 형성된 고체들 중에서 아주 특별한 몇몇 종류는 내부적으로 모종의 자기촉매autocatalysis 메커니즘을 획득할 수 있다. 쉽게 말해서, 자기촉매 메커니즘이란 어떤 화학 작용의 결과로 만들어지는 물질이 다시 그 화학 작용을 돕는 촉매로 작용하는 것이다. 생각해 보면, 생명이란 기본적으로 자신의 상태를 유지하는 데에 도움이 되는 다양한 물질을 만들어 내는 물질 상태라고 볼 수 있다. 그렇게 생각하면 생명이 자기촉매 메커니즘을 필요로 하는 것은 어찌 보면 당연하다.
궁극적으로 자기촉매 메커니즘은 자기조립self-assembly과 자기복제self-replication 작업을 수행할 수 있는 정도로까지 발전할 수 있다. 그리고 이 정도까지 고도로 조직화된 물질 상태는 가히 생명체라고 부를 수 있게 된다.
다만 처음에 발생한 생명체는 아주 초보적인 형태를 지닐 것이다. 하지만 아무리 초보적일지라도 일단 시작된 생명체는 돌연변이mutation와 적자생존survival of the fittest을 통해 꾸준히 진화하여 언젠가 지능과 자유의지를 지니는 고등 생명체로 발전할 수 있게 된다. 이것은 물론 다윈의 진화론Darwin’s theory of evolution이다.
지금까지 이 글을 읽고 있는 독자들 중에 어떤 이들은 필자가 생명체가 발생하는 메커니즘, 소위 생명의 기원origin of life을 너무 간단하게 설명한다고 느낄 것이다. 물론 그렇다. 생명의 기원은 필자가 매우 큰 관심을 가지고 있는 문제이지만, 이 문제를 심도 있게 논의하기에 필자의 식견은 매우 부족하다. 당연한 말 같지만, 이 문제의 궁극적인 해결은 필자가 조금이나마 알고 있는 물리학뿐 아니라, 현재 인류가 알고 있는 모든 지식의 범위를 벗어난다고 볼 수 있다. 앞으로 이 문제의 해결에 물리학, 특히 이론물리학이 어떠한 역할을 할 수 있을지 모르겠지만, 언젠가 해결되는 날이 온다면 필자가 그 답의 의미를 깨달을 수 있기를 진심으로 바라본다.
그런데 재미있게도 기존에 이미 이론물리학이 생명의 비밀을 밝히는 데 나름 중요한 역할을 했던 결정적인 예가 하나 있다.
바로 슈뢰딩거의 책 『생명이란 무엇인가?What is Life』이다. 이 책은 슈뢰딩거가 1943년 더블린 고등과학원Dublin Institute for Advanced Studies의 이론물리학 부장으로 재임할 당시에 더블린 트리니티 대학교Trinity College에서 수행한 대중 강연의 내용을 바탕으로 쓰였다.
크게 보아서 “생명이란 무엇인가?”의 주요 논지는 현재 이 글에서 필자가 전달하고자 하는 내용과 일맥상통한다. 아니, 솔직히 말해서 필자가 현재 이 글을 이런 논지로 쓰고 있는 이유가 바로 슈뢰딩거의 영향이라고 할 수 있다.
우선 생명이 존재하기 위해서 가장 중요한 조건은 엔트로피를 낮은 상태로 유지하는 것이다. 그런데 우리가 아는 한 열역학 제2법칙은 결코 위배되지 않는다. 그렇다면 생명은 어떻게 엔트로피를 지속적으로 낮게 유지할 수 있는 것일까?
다행히 열역학 제2법칙은 전체 시스템에서 엔트로피가 감소하지 않는다고 말할 뿐이다. 따라서 부분적으로는 언제나 엔트로피를 낮출 수 있다. 어찌 보면 생명체가 숨을 쉬고, 음식을 먹고, 운동을 하고, 번식을 하는 모든 행동은 엔트로피를 낮추는 수단에 불과하다. 생명체의 진정한 원동력은 음식이라기보다 “음의 엔트로피negative entropy”인 것이다.
엔트로피를 낮게 유지하기 위해서 생명체는 주변의 열적 요동으로부터 자기 자신을 지켜야 한다. 그리고 그러기 위해서 원자들은 서로 협동을 해서 단단한 구조를 만들어야 한다. 이 단단한 구조가 바로 고체, 혹은 결정crystal이다. 당연한 말 같지만, 생명체의 몸은 고체(와 그것을 유지하는 데에 필요한 액체)로 이루어져 있다.
그런데 고체에는 거칠게 말해서 두 가지 종류가 있다. 즉, 금속과 같이 원자들이 매우 규칙적인 배열 구조를 지니는 고체와 고분자와 같이 원자들이 약간 느슨한 배열 구조를 지지는 고체가 있다. 우선 고체 속 원자의 배열 구조가 매우 규칙적이면 열적 요동으로부터 매우 안전하게 보호된다는 장점이 있다. 하지만 이 경우 고체는 열적 요동으로부터 너무 완전하게 차단되어 결정론적으로 운동하는 기계에 불과하게 된다. 반면, 고체 속 원자의 배열 구조가 약간 느슨하게 되면 열적 요동으로부터 적당하게 보호되면서 결정론으로부터 탈출할 여지가 생긴다.
이 부분에서 절묘한 점이 발생한다. 열적 요동으로부터 보호되면서 결정론으로부터 탈출하는 것은 좋은데, 이러한 동적 균형을 지속적으로 유지하기 위해서는 고도로 복잡한 자기조직화self-organization가 필요하다. 하지만 이러한 자기조직화는 단번에 이루어질 수 없을 뿐만 아니라, 아무리 노력한다고 해도 단일 생명체는 결국 머지않아 열역학 제2법칙에 무너질 수밖에 없다.
이 난관을 헤쳐나가는 방법 중 하나는 자기복제를 하는 것이다. 자기 자신의 복사본을 여러 개 만들 수 있다면, 설사 자기 자신은 열역학 제2법칙에 굴복한다고 하더라도 복사본은 다시 새롭게 시작할 기회를 가질 수 있다. 다시 말해서, 시간과의 싸움을 다시 초기화initialization할 수 있는 것이다.
그런데 이 방법에는 문제가 하나 있다. 자기 자신을 복제하기 위해서 생명체는 자기 자신에 대한 정보를 담은 모종의 설계도blueprint를 몸 안에 품고 있어야 한다. 그리고 이 설계도를 품고 있는 부분은 만약의 경우를 대비해서 몸의 극히 일부분에 국한되어야 한다. 왜냐하면 만약 정보가 몸 전체에 광범위하게 퍼져 있다면 정보가 유실될 확률이 크기 때문이다.
문제는 생명체의 정보가 몸의 극히 일부, 즉 분자 수준의 작은 시스템에 저장된다면 열적 요동으로부터 보호되기 힘들다는 것이다. 그렇다면 생명체의 정보가 분자 수준의 작은 시스템에 저장되면서도 열적 요동으로부터 보호될 수 있는 방법이 있을까?
재미있게도 그 방법은 정보를 디지털digital의 형태로 저장하는 것이다.
예를 들어서 우리가 누군가로부터 어떤 정보를 전화로 들은 후에 다음 사람에게 전달하는 임무를 맡았다고 하자. 우리가 처음 전화로 들은 것은 생전 처음 들어 보는 어떤 동물의 울음소리이다. 우리가 다음 사람에게 제대로 된 정보를 전달하기 위해서는 이 동물의 울음소리가 지니는 특징을 정확하게 파악해야 한다.
우선 울음소리를 대충 흉내 내 볼 수 있을 것이다. 이 방법은 재미는 있겠지만, 과학적으로 좋은 방법은 아니다. 과학적으로 좋은 방법 중의 하나는 울음소리를 몇 개의 주파수로 분해한 후에 각 주파수 별로 얼마나 울음소리가 강한지를 측정하는 것이다. 이 방법은 “믿기 힘든 양자 Incredible Quantum [5]: 양자 삼위일체 1부”에서 배운 바 있는 푸리에 변환Fourier transform이다. 가령 10개의 대표 주파수에 대해서 상대적인 울음소리의 세기를 측정한다면 우리는 다음 사람에게 매우 정확한 정보를 전달할 수 있을 것이다.
이렇듯 연속적인 주파수에 대해서 모든 정보를 다 전달하려고 노력하는 대신에 불연속적인 몇몇 대표 주파수에 대해서 정보를 전달한다면 정보의 양은 떨어지더라도 질은 휠씬 좋아질 수 있다. 특히 대표 주파수가 이미 약속으로 정해져 있다면, 혹시 전달 과정에서 실수가 발생하더라도 쉽게 알아차릴 수 있다. 예를 들어서, 대표 주파수를 20Hz, 100Hz, 500Hz, 2,500Hz, 12,500Hz 와 같이 5배씩 증가한다고 약속을 했는데, 중간에 누가 실수로 500Hz 대신에 700Hz로 전달하게 되면, 쉽게 실수를 알아차리고 수정할 수 있을 것이다.
생명체의 정보도 디지털의 형태로 저장된다. 이는 다름 아니라 바로 DNA이다. DNA 는 A아데닌, adenine, T타이민, thymine, C시토신, cytosine, G구아닌, guanine로 표시되는 4가지 종류의 뉴클레오타이드nucleotide를 마치 디지털 신호의 0, 1처럼 사용하여 생명체의 정보를 저장한다. 즉, DNA에 담긴 생명체의 정보는 다름 아니라 A, T, C, G로 이루어진 염기 서열이다. [그림3]은 DNA의 분자 구조를 보여준다.
이런 방식으로 정보를 저장하면, 마치 디지털 신호에서 실수가 발생하면 쉽게 알아차릴 수 있듯이 DNA는 유전 과정에서 발생할 수 있는 실수를 쉽게 감지할 수 있다. 예를 들어서 타이민은 생명체가 살아있는 동안에 지속적으로 손상을 입어서 우라실uracil로 변형되는데, 이렇게 손상된 DNA는 쉽게 감지되어 소변으로 배출된다고 한다.
참고로 DNA가 자기복제를 하는 과정에서 뉴클레오타이드 자체가 바뀌는 것이 아니라 A, T, C, G로 이루어진 염기 서열의 순서가 부분적으로 뒤바뀌는 경우가 생길 수 있다. 이것도 유전 과정에서 발생하는 실수의 한 종류이다. 하지만 이러한 종류의 실수는 진화에 매우 중요한 역할을 한다. 이것은 바로 돌연변이이다.
물론 슈뢰딩거가 『생명이란 무엇인가?』를 쓸 당시에는 아직 DNA가 발견되지 않았다. 하지만 슈뢰딩거는 그 당시까지 발견된 생물학적인 사실과 이론물리학적인 관점에서 볼 때, 생명의 유전heredity에 관여하는 모종의 분자가 존재하며 이 분자의 행동 방식은 양자역학의 지배를 받을 것이라고 추정했다.
특히 양자역학은 분자 속 전자들이 정상파를 만드는 조건을 통해서 유전에 관여하는 분자의 기하학적인 구조를 불연속적으로 조절할 수 있다. 불연속은 디지털의 다른 말이다. 양자역학은 결국 유전에 관여하는 분자가 디지털의 형태로 생명체의 정보를 저장하는 것을 가능하게 하는 것이다. 슈뢰딩거는 이 분자를 “비주기적인 결정aperiodic crystal”이라고 불렀다.
자, 이제 생명의 기원을 떠나서 새로운 질서에 관한 논의로 다시 돌아가 보자. 앞서 언급했듯이, 모든 새로운 질서는 궁극적으로 고체의 형성, 즉 병진 대칭성의 자발적 붕괴로부터 시작한다고 볼 수 있다.
그런데 자발적 대칭성 붕괴를 통해서 깨지는 대칭성이 꼭 병진 대칭성일 필요는 없다. 사실 우리 우주가 존재하기 위해서는 병진 대칭성 이상으로 중요한 어떤 특정한 대칭성이 자발적으로 붕괴되어야만 한다. 이 중요한 자발적 대칭성 붕괴에 대해서는 아래에서 자세하게 이야기하게 될 것이다. [힌트: 사실 바로 밑에 있다.]
하지만 그전에 자발적 대칭성 붕괴를 일으키는 데에 양자역학이 어떠한 역할을 했는지 다시 한번 기억해 보자. 고체에서 병진 대칭성을 자발적으로 붕괴시키는 가장 핵심적인 요소는 입자들 간의 상호작용, 구체적으로 전자와 원자핵, 전자와 전자 사이의 전자기력electromagnetic force이다.
전자기력을 포함해서 우주에는 4가지의 근본적인 힘, 즉 상호작용이 있다. 바로 중력, 전자기력, 강력, 약력이다. 중력의 경우는 문제가 조금 복잡하기는 하지만 “믿기 힘든 양자 Incredible Quantum [4]: 게이지 대칭성”에서 배운 바에 따르면 모든 근본적인 힘은 게이지 대칭성gauge symmetry에 근거한다. 간단하게 말해서, 게이지 대칭성이란 측정 가능한 모든 물리량은 파동 함수의 위상을 임의로 바꾸더라도 전혀 변하지 않는다는 것이다. 다시 말해 모든 근본적인 힘은 파동 함수가 위상phase을 가진다는 사실에 기인한다.
그렇다면 결국 자발적 대칭성 붕괴, 그리고 그것으로 인해서 발생하는 모든 새로운 질서는 궁극적으로 파동 함수의 위상이 존재하기 때문이라고 볼 수 있다.
즉, 모든 새로운 질서는 양자역학 때문에 존재할 수 있다.
하지만 파동 함수의 위상은 일단 고체가 형성되고 나면 그 모습을 숨기고 미시 세계로 사라져 버린다. 우리는 파동 함수의 위상이 사라진 거시 세계에 살고 있으며, 거시 세계는 고전역학의 지배를 받는다. 다시 말해서, 양자역학은 고전역학에게 힘이라는 선물을 주고 미시 세계로 사라져 버린다. 이것은 다름 아니라 인류가 양자역학을 발견하는 데에 오랜 시간이 걸린 이유이다.
그렇다면 양자역학은 거시 세계에서 반드시 사라져야 하는가?
그렇지 않다. 거시적인 스케일에서도 파동 함수의 위상의 효과가 사라지지 않는 특별한 종류의 물질이 있다. 이 물질이 바로 본격적인 의미에서의 양자 물질quantum matter이다.
양자 물질은 크게 두 가지 종류로 구분된다. 하나는 페르미온fermion으로 이루어진 양자 물질이고 다른 하나는 보존boson으로 이루어진 양자 물질이다. 이어지는 다음 섹션에서는 각 종류를 대표하는 양자 물질에 대해서 이야기하고자 한다
페르미온 양자 물질의 대표: 양자 홀 상태
사실 페르미온, 구체적으로는 전자로 이루어진 양자 물질은 이미 이전에 자세하게 논의를 했다. “믿기 힘든 양자 Incredible Quantum [8]: 위상의 귀환”에서 이야기를 한 위상 절연체topological insulator가 바로 그것이다.
위상 절연체가 무엇인지를 한 문장으로 정리하면 다음과 같다.
“위상 절연체란 전자들이 위상학적으로 뻔하지 않은 에너지 띠topologically nontrivial energy band를 가득 채울 때 발생하는 절연체이다.”
우선 위상 절연체가 절연체, 즉 전기가 잘 통하지 않게 되는 이유는 간단하다. 위상학적으로 뻔하든 뻔하지 않든 간에 주어진 에너지 띠의 모든 상태를 빠짐없이 가득 채우고 나면 전자들은 더 이상 자유롭게 움직일 수 없기 때문이다.
다음으로, 위상 절연체에서 에너지 띠가 위상학적으로 뻔하지 않다는 것은 조금 긴 설명이 필요하다. 다행히도 이 설명은 이미 “믿기 힘든 양자 Incredible Quantum [8]: 위상의 귀환”에서 길고 자세하게 했다. 여기서는 구체적으로 설명을 반복하기보다는 재미있는 우화를 통해서 위상 절연체를 이해해 보고자 한다.
우화적으로 고체solid라는 나라에 전자electron라는 국민들이 살고 있다. 특히 전자들은 모두 블로흐 파동Bloch wave이라는 집을 짓고 살고 있는데, 블로흐 파동은 그것의 운동량, 즉 파수wave number로 구분된다. 파수는 블로흐 파동의 집주소home address라고 할 수 있다.
특히 고체 속 한 무리의 전자들은 큰 도시를 이루어 살고 있다. 이 도시의 이름은 브릴루앙 영역Brillouin zone이다.
(참고로, 고체 속에서 블로흐 파동과 브릴루앙 영역이 존재하는 진짜 물리적인 이유는 “믿기 힘든 양자 Incredible Quantum [10]: 더 높은 차원으로”에서 자세하게 설명하였다.)
마침 이 나라에는 해밀토니안Hamiltonian이라는 왕이 살고 있다. 해밀토니안 왕은 브릴루앙 영역을 자신이 전체적으로 지배하고 있는 위성인 스핀spin 달로 통째로 옮기고 싶어한다. 다시 말해서, 해밀토니안 왕은 브릴루앙 영역이라는 하나의 큰 도시를 스핀 달이라는 위성으로 옮기는 장대한 우주 이주 프로젝트를 실행하고자 한다.
그런데 스핀 달의 중심부에는 자기 홀극magnetic monopole이라고 부르는 이상한 핵이 자리 잡고 있다. 자기 홀극은 북극과 남극이라는 두 개의 극을 가지지 않고 하나의 극으로만 이루어져 있다. 따라서 스핀 달에서는 나침반이 북쪽을 가리키지 않고 우주를 향한다. 참고로 스핀 달의 관광 슬로건은 “북쪽이 아니라 위쪽으로Upward, not Northward”이다.
해밀토니안 왕은 도시 계획을 잘 세워서 브릴루앙 영역이 이 이상한 스핀 달의 전 표면을 빠짐없이 다 감싸기를 바란다. 정확한 이유는 모르겠지만 아마도 해밀토니안 왕은 스핀 달의 중심부에 자기 홀극이 있다는 사실을 숨기고 싶어하는 것 같다. 만약 해밀토니안 왕이 성공하면, 브릴루앙 영역은 위상 절연체 왕국이 될 것이다. 위상 절연체 왕국이 꼭 좋은 나라가 될지는 모르겠지만, 적어도 위상학적으로는 뻔하지 않을 것이다.
자, 이제 우화를 떠나서 다시 구체적인 위상 절연체의 이야기로 돌아가 보자.
위에서 설명한 바에 따르면 위상 절연체는 근본적으로 자기 홀극이 존재하기 때문에 생긴다. 다만 위상 절연체의 자기 홀극은 실 공간이 아니라 가상의 공간에 존재한다.
그런데 만약 가상의 공간이 아니라 실 공간에 진짜로 자기장이 걸리면 어떻게 될까?
이 경우에 나타나는 위상 절연체가 바로 양자 홀 상태quantum Hall state이다. 사실 양자 홀 상태는 위상 절연체보다 훨씬 먼저 발견되었다. 노벨 물리학상도 3번이나 수여 되었다. 바로 1985년 수상한 클라우스 폰 클리칭Klaus von Klitzing, 1998년 공동 수상한 로버트 로플린Robert Laughlin, 홀스트 스토머Horst Stormer, 대니얼 추이Daniel Tsui, 2016년 수상한 데이비드 타울레스David Thouless이다. (참고로 2016년 노벨 물리학상의 공동 수상자인 마이클 코스털리츠Michael Kosterlitz와 던컨 할데인Duncan Haldane의 업적은 직접적으로는 양자 홀 효과와 관련이 없다.)
간단하게 말해서, 양자 홀 효과는 위상 절연체의 아버지이다.
자, 이제 그럼 양자 홀 효과를 구체적으로 이해해 보자.
양자 홀 효과를 구체적으로 이해하기 위해서는 자기장이 걸린 상황을 묘사하는 슈뢰딩거 방정식을 정확하게 풀 수 있어야 한다. 하지만 그렇게 하기 전에 마치 보어의 원자 모형처럼 고전역학과 양자역학을 적절히 잘 섞은, 소위 준고전적인 이론semiclassical theory을 하나 세워보고자 한다. 사실 이와 비슷한 준고전적인 이론은 이전에 누군가 제안했을 확률이 매우 높지만, 필자 개인적으로는 알지 못한다. 필자가 아는 한, 이 준고전적인 이론은 필자가 독자적으로 개발했다.
필자의 무지를 핑계 삼아 이 준고전적인 이론을 보어의 원자 모형에 빗대어 “박권의 사이클로트론 모형cyclotron model”이라고 명명해보자.
사이클로트론이라는 명칭이 들어가는 이유는 다음과 같다. 우선 전하를 지니는 입자는 자기장 하에서 로렌츠 힘을 받는다. 로렌츠 힘은 회전 운동을 야기한다. 이렇게 로렌츠 힘에 의한 회전 운동을 이용해서 입자를 빠르게 가속시키는 장치를 사이클로트론이라고 부른다. 참고로 사이클로트론은 현대 입자 가속기particle accelerator의 원형이라고 볼 수 있다. 필자의 사이클로트론 모형의 목적은 자기장 하에서 회전하는 입자가 가지는 에너지 고유값을 준고전적인 근사 방법을 써서 구하는 것이다.
우선 필자의 사이클로트론 모형은 보어의 원자 모형과 같이 원형 궤도에서 파동 함수가 정상파를 만드는 조건으로부터 시작한다.
$$2\pi r=n\lambda$$
여기서 \(r\)은 원형 궤도의 반지름이고 \(\lambda\)는 파동 함수의 파장wave length이다. 이제 드브로이의 파동-입자 이중성wave-particle duality을 써서 위 조건을 다시 쓰면 우리에게 익숙한 보어의 양자화 조건을 얻는다.
$$rp=n\hbar$$
여기서 \(p\)은 전자의 운동량이다. 보어의 양자화 조건을 새삼스럽게 다시 유도한 이유는 자기장 하에서 운동량이 단순히 질량 곱하기 속도가 아니라는 사실을 강조하기 위함이다.
다시 말해서, “믿기 힘든 양자 Incredible Quantum [4]: 게이지 대칭성”에서 배웠듯이 운동량에는 두 가지 종류가 있다. 바로 역학적 운동량mechanical momentum \(m{\bf v}\)와 카노니칼 운동량canonical momentum \({\bf p}\)이다. 이 두 가지 운동량은 다음과 같이 연결된다.
$${\bf p}=m{\bf v}+\frac{e}{c}{\bf A}$$
여기서 \(e\)는 전자의 전하이고 \({\bf A}\)는 자기장을 주는 벡터 퍼텐셜이다. 구체적으로 \(z\) 방향을 향하는 자기장을 주는 벡터 퍼텐셜은 다음과 같이 정할 수 있다.
$${\bf A}=\frac{1}{2}B(-y,x,0)=\frac{1}{2}Br(-\sin{\theta},\cos{\theta},0)=\frac{1}{2}Br\hat{\theta}$$
여기서 \(\theta\)는 주어진 위치와 원점을 연결하는 직선이 \(x\) 축과 이루는 각도이고 \(\hat{\theta}\)는 이러한 각도 방향으로의 단위 벡터이다. 앞서 설명했듯이 자기장 하에서 입자는 회전 운동을 한다. 이제 입자의 속도 벡터를 \(\hat{\theta}\)를 이용해서 다음과 같이 표현할 수 있다.
$${\bf v}=v\hat{\theta}$$
이를 종합해서 역학적 운동량과 카노니칼 운동량 사이의 관계식을 \(\hat{\theta}\) 방향에 대해서 다시 쓰면 다음과 같다.
$$p=mv-\frac{|e|B}{2c}r$$
위에서 전자의 전하가 음이라는 성질을 썼다. (참고: 엄밀하게 말해 전자의 전하가 음수일 때 전자의 속도가 \(\hat{\theta}\) 방향으로 양수가 된다는 성질을 썼다.) 최종적으로 보어의 양자화 조건은 다음과 같이 쓰일 수 있다.
$$r\left(mv-\frac{|e|B}{2c}r \right)=n\hbar$$
이제 회전 운동에 의한 원심력과 자기장에 의한 로렌츠 힘이 서로 균형을 이룬다는 조건을 써 보자.
$$\frac{mv^2}{r}=\frac{|e|}{c}vB$$
참고로 보어의 원자 모형에서는 원심력과 쿨롱 상호작용에 의한 전기력이 균형을 이룬다는 조건이 쓰였다. 위 공식은 약간 다듬으면 다음과 같이 쓰인다.
$$mv=\frac{|e|B}{c}r$$
이제 보어의 양자화 조건과 힘의 균형 조건을 동시에 만족하는 해를 찾아서 입자의 에너지, 즉 운동 에너지를 계산하면 다음과 같은 결론에 이를 수 있다.
$$E=\frac{1}{2}mv^2=\hbar\omega_c n$$
여기서 \(\omega_c=|e|B/mc\)는 사이클로트론 진동수cyclotron frequency라고 불린다. 참고로 위 공식에서 운동 에너지는 항상 0보다 크거나 같아야 하므로, 양자수 \(n\)도 항상 0보다 크거나 같은 정수이어야 한다.
위 공식은 슈뢰딩거 방정식을 정확히 풀어서 얻을 수 있는 에너지 고유값과 거의 같지만, 딱 한 가지 면에서 다르다. 이어지는 논의에서 더 자세히 유도하겠지만, 정확한 에너지 고유값은 다음과 같다.
$$E=\hbar\omega_c \left( n+\frac{1}{2} \right)$$
딱 보면 알겠지만 정확한 에너지 고유값과 준고전적인 에너지 고유값의 차이는 괄호 안의 \(1/2\)이라는 상수이다. 즉, 두 에너지 고유값 사이의 차이는 \(\hbar\omega_c/2\) 만큼의 상수 에너지이다. 참고로 이 상수 에너지는 영점 에너지zero-point energy라고 불린다.
상수 에너지의 차이가 뭐 그리 중요한가라는 질문을 가질 수 있다. 에너지의 기준은 항상 재조정할 수 있기 때문이다. 하지만 놀랍게도 이 상수 에너지는 상황에 따라서 매우 중요한 현상을 초래할 수 있다. 이것이 영점 에너지라는 매우 특별한 이름이 붙어있는 이유이다. 영점 에너지의 물리적인 의미는 “믿기 힘든 양자 Incredible Quantum [13]: 상대성과 양자, 통합되다”에서 더 자세하게 논의할 예정이다.
사실 잘 생각해 보면, 준고전적인 이론을 통해서 얻어지는 에너지 고유값이 슈뢰딩거 방정식을 통해서 얻어지는 정확한 에너지 고유값과 완벽하게 일치할 이유는 전혀 없다. 실제로 영점 에너지만큼의 차이가 있기도 하다. 하지만 “믿기 힘든 양자 Incredible Quantum [11]: 양자 물질 상태”에서 설명했듯이, 준고전적인 이론은 묘하게도 정확한 양자역학의 결과와 상당 부분 잘 들어맞는다. 특히 에너지 고유값이 \(\hbar\omega_c\) 만큼의 간격을 가지고 양자화된다는 사실은 정확하다.
참고로 이렇게 자기장 하에서 양자화되는 에너지 준위를 전문적으로 란다우 준위Landau level라고 부른다.
자, 이제는 자기장이 걸린 상황을 기술하는 슈뢰딩거 방정식을 정확하게 풀어보자.
항상 그렇듯이 슈뢰딩거 방정식은 해밀토니안을 쓰는 것으로부터 출발한다.
$$H=\frac{1}{2m}\left( {\bf p}+\frac{|e|}{c}{\bf A} \right)^2$$
여기서 \({\bf A}\)는 자기장을 주는 벡터 퍼텐셜이다. 편의상 역학적 운동량을 다음과 같이 \(\boldsymbol{\Pi}\)라는 기호를 써서 표현해 보자.
$$\boldsymbol{\Pi}=m{\bf v}={\bf p}+\frac{|e|}{c}{\bf A}$$
그렇다면 해밀토니안은 다음과 같이 간단하게 쓰인다.
$$H=\frac{\boldsymbol{\Pi}^2}{2m}$$
이제부터 위 해밀토니안을 란다우 해밀토니안Landau Hamiltonian이라고 부르자
여기서 중요한 사실은 역학적 운동량의 \(x\)와 \(y\) 성분이 더 이상 서로 교환가능하지 않다는 것이다. 구체적으로 역학적 운동량의 \(x\)와 \(y\) 성분인 \(\Pi_x\)와 \(\Pi_y\)는 다음과 같은 교환 관계식을 만족한다.
$$[\Pi_x,\Pi_y]=-i\frac{\hbar|e|}{c}\left( \frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y} \right)=-i\frac{\hbar|e|}{c}B=-i\frac{\hbar^2}{l_B^2}$$
여기서 \(l_B=\sqrt{\hbar c/|e|B}\)는 자기 길이magnetic length라고 불린다. (참고로 여기서는 \(B\)가 양수인 경우만을 고려했지만, 음수로 확장하는 것은 그리 어렵지 않다.)
앗, 혹시 위 교환 관계를 보면 무엇인가 생각나지 않는가? 사실 위 교환자는 위치와 운동량 사이에 존재하는 교환 관계와 매우 비슷하다.
$$[x,p]=i\hbar$$
“믿기 힘든 양자 Incredible Quantum [6]: 양자 삼위일체 2부”에서 배운 것을 기억해 보면, 위치와 운동량 사이의 교환 관계는 하이젠베르크의 불확정성 원리를 의미한다. 즉, 위 교환 관계는 위치와 운동량을 동시에 정확하게 확정하는 것이 불가능하다는 것을 의미한다.
$$\Delta x\Delta p \geq \frac{\hbar}{2}$$
비슷하게 \(\Pi_x\)와 \(\Pi_y\) 사이의 교환 관계는 자기장 하에서 \(x\)와 \(y\) 방향으로 속도를 동시에 정확하게 확정하는 것이 불가능하다는 것을 의미한다. 특히 자기장이 세지면 세질수록 불확정성의 정도도 커진다.
자, 이제 그렇다면 란다우 해밀토니안은 구체적으로 어떻게 풀어야 할까?
재미있게도 란다우 해밀토니안은 앞선 “믿기 힘든 양자 Incredible Quantum [11]: 양자 물질 상태”에서 각운동량의 양자화를 위해서 도입한 “사다리 연산자ladder operator”와 매우 유사한 연산자를 정의해서 풀 수 있다. 기억을 되살리기 위해서, 각운동량의 양자화를 위한 사다리 연산자는 다음과 같은 올림raising 및 내림lowering 연산자로 구성되었다.
$$L_+=L_x+iL_y$$
$$L_-=L_x-iL_y$$
이제 란다우 해밀토니안을 위한 사다리 연산자는 다음과 같이 정의된다.
$$a^\dagger=\frac{l_B/\hbar}{\sqrt{2}}(\Pi_x+i\Pi_y)$$
$$a=\frac{l_B/\hbar}{\sqrt{2}}(\Pi_x-i\Pi_y)$$
아래 보겠지만 \(a^\dagger\)와 \(a\)는 각각 올림과 내림 연산자의 역할을 한다. 참고로 \(a^\dagger\)와 \(a\)는 다음과 같은 교환 관계식을 만족한다.
$$[a,a^\dagger]=1$$
위 교환 관계식은 매우 중요하므로 독자들은 꼭 기억하기를 바란다.
사실 올림과 내림 연산자가 편리한 이유는 해밀토니안이 그들의 곱으로 깔끔하게 표현되기 때문이다. 즉, 올림 연산자와 내림 연산자의 곱을 계산해 보면 다음과 같다.
$$a^\dagger a=\frac{l_B^2}{2\hbar^2}(\Pi_x^2+\Pi_y^2-i[\Pi_x,\Pi_y])$$
여기서 앞선 \(\Pi_x\)와 \(\Pi_y\) 사이의 교환 관계를 이용하면 아래와 같은 결론에 이를 수 있다.
$$H=\hbar\omega_c\left( a^\dagger a +\frac{1}{2} \right)$$
(참고로 위와 같은 수학적인 형태를 지니는 해밀토니안은 매우 중요하다. 나중에 보겠지만, 이 해밀토니안은 빛, 즉 광자photon를 기술한다.)
자, 이제 사다리 연산자의 성질을 적절히 잘 이용하면 란다우 해밀토니안을 대각화diagonalization할 수 있다. 구체적으로 란다우 해밀토니안이 \({\cal E}\)이라는 에너지 고유값을 갖는다고 하자. 특히 이러한 에너지 고유값을 가지는 에너지 고유상태를 \(|{\cal E}\rangle\)이라는 표시하면 \(|{\cal E}\rangle\)은 다음과 같은 슈뢰딩거 방정식을 만족한다.
$$H|{\cal E}\rangle={\cal E}|{\cal E}\rangle$$
여기서 각운동량을 양자화할 때 배운 바를 응용해서 \(|{\cal E}\rangle\)에 올림 연산자를 작용하면 어떤 일이 벌어지는지 알아보자. 즉, 아래 파동 함수가 에너지 고유상태인지, 그리고 그렇다면 어떠한 에너지 고유값을 가지는지 알아보고자 한다.
$$a^\dagger|{\cal E}\rangle$$
자, 그러기 위해서 위 파동 함수에 해밀토니안을 작용해 보자.
$$H a^\dagger|{\cal E}\rangle=(a^\dagger H+[H,a^\dagger])|{\cal E}\rangle$$
위에서 우리는 \(H\)와 \(a^\dagger\)의 순서를 바꾸려고 노력했다. 그런데 그러는 과정에서 그들 사이의 교환자 \([H,a^\dagger]\)가 나타났다. 이제 우리는 \([H,a^\dagger]\)가 무엇인지 알아야 한다.
위에서 매우 중요하다고 언급한 \(a^\dagger\)와 \(a\) 사이의 교환 관계식을 기억하는가? 지금이 바로 그것이 중요하게 쓰이는 순간이다. 즉, \(a^\dagger\)와 \(a\) 사이의 교환 관계식을 쓰면 다음과 같은 교환 관계식을 유도할 수 있다.
$$[H,a^\dagger]=\hbar\omega_c a^\dagger$$
이제 위 교환 관계식을 이용하면 다음과 같은 결론에 이를 수 있다.
$$H a^\dagger|{\cal E}\rangle=(a^\dagger H+\hbar\omega_c a^\dagger)|{\cal E}\rangle=({\cal E}+\hbar\omega_c) a^\dagger |{\cal E}\rangle$$
결론적으로 \(a^\dagger|{\cal E}\rangle\)는 정말 에너지 고유상태이며, 그것의 에너지 고유값은 \({\cal E}+\hbar\omega_c\)이다. 비슷한 작업을 내림 연산자에 대해서 수행하면 \(a|{\cal E}\rangle\)도 에너지 고유상태이며, 그것의 에너지 고유값은 \({\cal E}-\hbar\omega_c\)라는 사실을 알 수 있다.
자, 이것이 의미하는 바는 무엇인가?
수학적으로 보면 이것은 어떤 에너지 고유값 \({\cal E}\)이 존재하면 그것을 포함한 모든 에너지 고유값은 다음과 같이 양자화된다는 것을 의미한다.
$$\cdots,\; {\cal E}-2\hbar\omega_c,\; {\cal E}-\hbar\omega_c,\; {\cal E},\; {\cal E}+\hbar\omega_c,\; {\cal E}+2\hbar\omega_c,\; \cdots$$
그런데 해밀토니안의 수학적인 형태를 보면 에너지 고유값은 음수가 될 수 없다. (퀴즈: 왜 그럴까?) 따라서 위 에너지 고유값의 사슬은 어느 시점에서 끝나야 한다. 다시 말해서, 사슬의 어느 시점에서 내림 연산자를 한 번 더 작용하면 에너지 고유상태가 완전히 사라져야 한다. 이렇게 내림 연산자를 작용하면 마지막으로 사라지는 에너지 고유상태를 \(|{\cal E}_0\rangle\)라고 하자.
$$a|{\cal E}_0\rangle=0$$
이제 위 공식에 올림 연산자를 작용해 보자.
$$a^\dagger a|{\cal E}_0\rangle=0$$
물론 우변은 당연히 0이다. 그런데 좌변은 자세히 보면 거의 해밀토니안과 같다. 즉, 위 공식은 양변에 같은 양을 적절히 잘 더하면 다음과 같이 다시 쓸 수 있다.
$$\left(a^\dagger a+\frac{1}{2}\right)|{\cal E}_0\rangle=\frac{1}{2}|{\cal E}\rangle$$
다시 말해서 \(|{\cal E}_0\rangle\)의 에너지 고유값은 \({\cal E}_0=\hbar\omega_c/2\)이다. 결론적으로 모든 에너지 고유값은 다음과 같이 양자화된다.
$${\cal E}=\hbar\omega_c\left( n+\frac{1}{2} \right)$$
여기서 \(n\)은 0보다 크거나 같은 정수이다. 위 공식은 물론 앞에서 언급한 정확한 에너지 고유값을 표현하는 공식이다.
기억을 되살려 보면 위와 같이 자기장 하에서 에너지 고유값이 양자화되는 고유상태를 란다우 준위라고 부른다고 했다. 기본적으로 각각의 란다우 준위는 앞서 위상 절연체에 관련해서 설명한 “위상학적으로 뻔하지 않은 에너지 띠” 하나에 해당한다. 즉, 모든 란다우 준위는 마치 각각 자기 홀극을 하나씩 품고 있는 위상학적으로 뻔하지 않는 에너지 띠처럼 행동하게 된다.
여기서 주목할 사실은 보통의 위상 절연체에서는 위상학적으로 뻔하지 않은 에너지 띠가 한 개, 혹은 적은 수의 몇 개만 만들어지는 반면에 자기장 하에서 란다우 준위는 무수히 많이 만들어진다는 것이다. 앞선 우화의 예를 들면, 스핀 달이 무수히 많이 생기는 것과 같다.
이러한 상황에서 전자의 개수를 증가시키면 각각의 란다우 준위는 하나씩 순차적으로 가득 채워지게 된다. 이는 마치 기존에 알고 있던 위상 절연체가 하나씩 순차적으로 연거푸 발생하는 것과 같다. 다시 한번 앞선 우화의 예를 들면, 무수히 많은 스핀 달에 하나씩 순차적으로 우주 이주 프로젝트를 실행하는 것과 같다.
잠깐, 여기서 “믿기 힘든 양자 Incredible Quantum [8]: 위상의 귀환”과 “믿기 힘든 양자 Incredible Quantum [10]: 더 높은 차원으로”에서 배운 내용 하나를 기억해 보자. 그때 배우기를 위상 절연체는 필연적으로 시스템의 경계, 즉 표면이나 에지edge에서 소위 “에지 상태edge state”를 발생시킨다. 이러한 에지 상태의 존재는 전자들이 시스템 내부로는 잘 흐를 수 없지만 표면이나 에지를 따라서는 자유롭게 흐를 수 있다는 것을 의미한다. 이것이 바로 위상 절연체의 가장 중요한 성질 중의 하나이다.
결론적으로 위상 절연체가 발생하면 시스템의 경계에 에지 상태가 만들어진다. 특히 위상학적으로 뻔하지 않은 에너지 띠인 란다우 준위가 하나씩 순차적으로 가득 채워질 때마다 새로운 에지 상태가 하나씩 만들어진다. 그리고 새로운 에지 상태가 하나씩 만들어진다는 것은 전자들이 자유롭게 흐를 수 있는 전도 채널conduction channel이 하나씩 새롭게 생긴다는 것을 의미한다.
자, 여기서 노벨 물리학상이 수여된 중요한 발견이 얻어진다. 바로 그 유명한 TKNN 공식이 바로 그것이다. 우선, 다짜고짜 TKNN 공식이 무엇인지 기술하면 다음과 같다. (참고로, TKNN공식에서 TKNN은 해당 공식이 처음 유도된 논문을 쓴 공저자 4명의 이름의 이니셜을 딴 것이다. 즉, “Thouless-Kohmoto-Nightingale-den Nijs”이다.)
TKNN 공식이란, 란다우 준위가 하나씩 순차적으로 가득 채워질 때마다 소위 “홀 전도도Hall conductance”라는 물리량이 어떤 값의 정수배로 한 칸씩 양자 도약quantum jump을 하게 된다는 것을 말해주는 공식이다.
이제 TKNN 공식에 대해서 조금 더 자세하게 설명해 보자.
우선 홀 전도도를 포함해서 전도도란 저항의 역수이다. 보통의 전도도는 외부에서 시스템에 전압을 걸어줄 때 전류가 얼마나 잘 흐르는가를 말해주는 양이다. 즉, 간단하게 말해서, 전도도는 전류를 전압으로 나눈 값이다. 당연한 말 같지만, 보통의 경우라면 전류는 물론 걸어준 전압의 방향으로 흐를 것이다.
하지만 자기장이 걸리면 상황이 조금 다르다. 로렌츠 힘으로 인해서 전류가 휠 수 있기 때문이다. 이러한 상황에서는 두 가지 종류의 전도도가 있다. 하나는 위에서 설명한 보통의 전도도이고 다른 하나는 홀 전도도이다. 구체적으로 홀 전도도는 \(x\) 방향으로 걸어준 전압을 걸어줄 때 \(y\) 방향으로 전류가 얼마나 잘 흐르는가를 말해주는 양이다.
TKNN 공식에 따르면 홀 전도도 \(\sigma_H\)는 가득 채워진 란다우 준위의 개수 \(n\)에 비례한다.
$$\sigma_H=\frac{e^2}{h}n$$
여기서 정말 놀라운 사실은 홀 전도도가 아주 근본적인 물리량인 전자의 전하량 \(e\)과 플랑크 상수 \(h\)에만 의존한다는 사실이다.
사실 정확히 같은 내용이기는 하지만, 전도도보다 조금 더 익숙한 저항resistance, 즉 홀 전도도 대신에 홀 저항Hall resistance으로 TKNN 공식을 표현하면 다음과 같다. 참고로 저항은 전도도의 역수이다.
$$R_H=\frac{R_K}{n}$$
여기서 \(R_K=h/e^2\)은 1980년 양자 홀 효과를 처음 실험으로 발견한 클라우스 폰 클리칭의 이름을 따서 폰 클리칭 상수von Klitzing constant라고 불린다. 참고로 \(R_K\)는 대략 25.812 \(k\Omega\)이다.
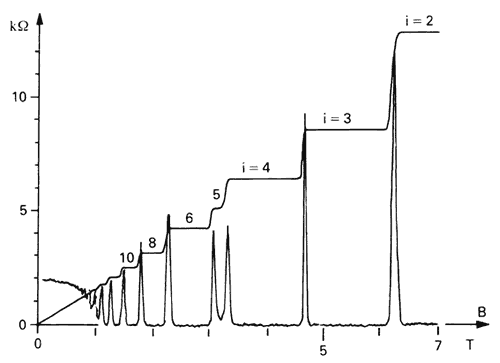
이것이 다름 아니라 바로 양자 홀 효과quantum Hall effect이다. 참고로 [그림4]는 전형적인 양자 홀 효과를 보여준다.
지금까지 이 글을 읽고 있는 독자들은 이미 느끼고 있겠지만, 양자 홀 효과를 구체적으로 설명하는 것은 그리 쉽지 않다. 사실 양자 홀 효과는 필자에게 아주 특별한 주제이다. 필자의 박사 학위 주제이기 때문이다. 그래서 필자는 그동안 다양한 지면을 통해서 양자 홀 효과를 설명할 기회가 있었는데, 그럴 때마다 독자에게 설명하는 것이 어렵다고 느끼곤 했다.
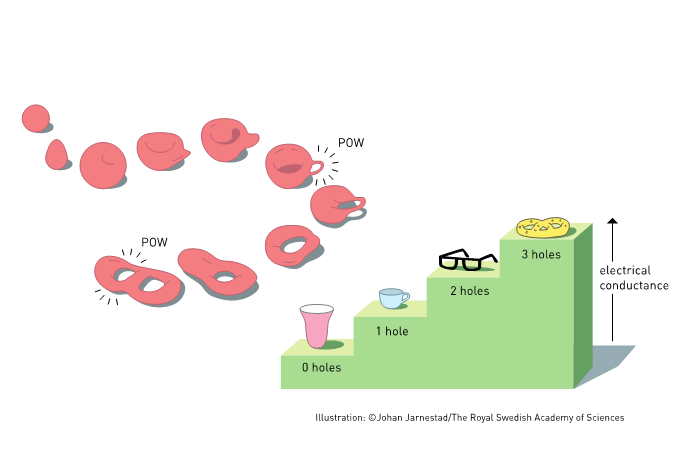
2016년, TKNN 공식을 발견한 사람들 중의 한 명인 타울레스에게 노벨 물리학상이 수여 되었을 때, 노벨 위원회도 일반 대중에게 양자 홀 효과를 쉽게 설명하는 것이 불가능하다고 생각했던 것 같다. 그래서 그들은 양자 홀 효과를 만화로 설명하기로 결심한다. 아래 [그림5]가 바로 그 만화이다.
우선 만화의 왼쪽 부분을 보자. 여기서는 찰흙과 같이 성형이 쉬운 물질을 주물럭거려서 손잡이가 하나 달린 컵을 만들고, 다시 더 주물럭거려서 도넛doughnut처럼 보이게 하고, 결국 구멍을 하나 더 뚫어서 구멍이 두 개 달린 프레첼pretzel 같은 모양을 만드는 과정이 단계적으로 표현되어 있다. 참고로 구멍이 한 개 뚫린 때마다 “뻥POW” 소리를 붙인 것이 재미있다.
당연한 말 같지만 구멍은 한 개, 두 개와 같이 자연수 개수로만 뚫릴 수 있다. 예를 들어서, 구멍은 0.5개 뚫릴 수 없다. 그리고 구멍의 개수는 3차원에 존재하는 덩어리 물체를 아무리 주물럭거려도 아예 새로운 구멍을 내지 않는 한 그 값이 바뀌지 않는다. 이 말 자체는 너무나도 자명하지만, 구멍의 개수가 “주물럭거리는 변형”에 대하여 변하지 않는 양이라는 개념은 생각보다 훨씬 심오한 수학과 깊게 연결되어 있다. 바로 가우스-보네 정리Gauss-Bonnet theorem라고 불리는 수학 정리이다.
가우스-보네 정리를 이해하기 위해서는 표면의 곡률curvature이라는 개념을 알아야 한다. 불행히도 여기서 곡률의 개념을 자세하게 설명할 수는 없다. 다만 지금으로서는 곡률이란 표면이 휘는 정도를 나타내는 양이라고 대략 이해하면 될 것 같다. 가우스-보네 정리에 따르면 3차원에 존재하는 덩어리 물체의 표면의 곡률curvature을 다 더한 값은 한 가지 조건 하에서 “주물럭거리는 변형”에 대해서 전혀 변하지 않는다. 예리한 독자들은 이미 예상했겠지만, 그 조건은 물체에 구멍을 뚫지 않는다는 조건이다.
구체적으로 가우스-보네 정리에 따르면, 3차원 덩어리 물체의 표면의 곡률의 총합은 구멍의 개수에 비례한다. 참고로 구멍의 개수는 국문으로는 종수 혹은 손잡이수, 영문으로는 지너스genus라고 불린다.
자, 이제 비유적으로 전자로 가득 채워지는 란다우 준위의 개수가 3차원에 존재하는 어떤 덩어리 물체의 구멍의 개수에 해당한다고 하자. 앞서 설명했듯이 각각의 란다우 준위는 자기 홀극을 하나씩 품고 있는 위상학적으로 뻔하지 않는 에너지 띠이다. 따라서 비유적으로 자기 홀극의 개수는 구멍의 개수에 해당한다. 그렇다면 결국 홀 전도도는 구멍의 개수에 비례하게 된다.
다시 만화로 돌아가 보자. 만화의 오른쪽 부분은 전기 전도도electrical conductance가 가공의 3차원 덩어리 물체에 구멍이 하나씩 뚫릴 때마다 마치 계단처럼 양자 도약을 하는 상황을 보여준다.
우리는 노벨 위원회의 만화를 완벽하게 이해했다!
보존 양자 물질의 대표: 보즈-아인슈타인 응축과 초유체
이제는 보존 양자 물질의 대표 주자를 만나볼 때가 되었다.
그러기 위해서 “믿기 힘든 양자 Incredible Quantum [11]: 양자 물질 상태”에서 배운 내용 하나를 기억해 보자. 그때 배우기를 우주의 모든 입자는 두 종류로 구분된다고 했다. 바로 페르미온과 보존이다.
페르미온은 파울리의 배타 원리를 만족한다. 그리고 파울리의 배타 원리는 구별 불가능한 페르미온들로 이루어진 다체 파동 함수many-body wave function의 대칭성에 기인한다. 즉, “믿기 힘든 양자 Incredible Quantum [11]: 양자 물질 상태”에서 배운 바에 따르면, 구별 불가능한 페르미온들로 이루어진 시스템의 동역학을 기술하는 다체 파동 함수는 임의의 두 페르미온, 예를 들어서 1번과 2번 페르미온을 교환하는 것에 대해서 \(-1\)이라는 부호를 갖는다.
$$\Psi_{\rm fermion}({\bf r}_2,{\bf r}_1,\cdots,{\bf r}_N)= -\Psi_{\rm fermion}({\bf r}_1,{\bf r}_2,\cdots,{\bf r}_N)$$
여기서 \({\bf r}_1, {\bf r}_2\)는 1번과 2번 페르미온의 위치 벡터이다. 이때 만약에 \({\bf r}_1\)과 \({\bf r}_2\)가 서로 같게 되면 파동 함수는 사라진다. 즉, 두 개의 구별 불가능한 페르미온이 같은 위치에 존재하면 파동 함수는 사라진다. 이는 다름 아니라 파울리의 배타 원리이다.
보존의 경우에는 임의의 두 보존을 교환할 때 아무런 부호 차이가 발생하지 않는다.
$$\Psi_{\rm boson}({\bf r}_2,{\bf r}_1,\cdots,{\bf r}_N)= \Psi_{\rm boson}({\bf r}_1,{\bf r}_2,\cdots,{\bf r}_N)$$
자, 이제 그렇다면 페르미온의 경우와 다르게 두 개의 구별 불가능한 보존은 같은 위치에 존재한다고 해도 아무런 일이 발생하지 않을 것처럼 보인다. 과연 그럴까?
이 글을 읽고 있는 독자들 중에 우주의 입자가 페르미온과 보존으로 구분된다고 할 때, 둘 사이에 무엇인가 상호대칭적인 구조가 있을 것 같다는 느낌이 든 사람이 있다면 당신은 벌써 물리학자이다.
직관적으로 말해서 페르미온이 파울리의 배타 원리를 통해서 서로를 밀어낸다면, 보존은 반대로 서로를 끌어당긴다. 단, 이러한 직관은 조심스럽게 사용되어야 한다. 왜냐하면 파동 함수의 대칭성에 기인하는 통계 법칙은 전자기력과 같은 근본적인 힘에 의해서 발생하는 상호작용과는 직접적인 연관성이 없기 때문이다.
다시 말해서, 파울리의 배타 원리는 힘의 원리가 아니다. 두 개의 구별 불가능한 페르미온이 서로를 배타하는 이유는 그들 사이에 밀어내는 힘이 있어서가 아니다. 비슷하게 보존이 서로를 끌어당긴다고 표현할 때에도 실제로 그러한 힘이 존재하는 것은 아니다. 다만 그럼에도 불구하고 보존은 모두 “단결”해서 단 하나의 상태로 뭉치려는 성질이 있다. 이렇게 보존이 상호작용의 도움 없이 서로 뭉치려는 현상을 보즈-아인슈타인 응축Bose-Einstein condensation이라고 한다.
참고로 보즈-아인슈타인 응축은 이름 그대로 두 물리학자의 합작품이다. 인도 물리학자였던 사티엔드라 보즈Satyendra Nath Bose는 아인슈타인에게 흑체 복사blackbody radiation를 기술하는 플랑크의 법칙을 설명하기 위해서 자신이 고안한 이론을 담은 편지를 보낸다. 보즈가 고안한 이론의 핵심은 빛이 알갱이, 즉 광자로 양자화되어 있으며 광자들은 서로 구별 불가능하다는 가정이었다.
보즈의 이론에 감명을 받은 아인슈타인은 1924년 영문으로 쓰인 보즈의 원논문을 손수 독일어로 번역해서 저명한 독일 물리학 저널인 “Z. Physik”에 보즈의 이름으로 대신 제출해 준다. (보즈의 원논문은 사실 이미 이전에 영국 물리학 저널인 “Philosophical Magazine”에 제출되었으나 거부되었다고 한다.) 무명이었던 보즈는 이 논문을 통해 단숨에 세계적으로 유명한 물리학자가 된다. 나중에 아인슈타인은 같은 원리를 광자뿐만 아니라 일반적인 입자로 확장하여 소위 보즈-아인슈타인 통계Bose-Einstein statistics를 발견한다.
이제 다시 본 논의로 돌아가 보자. 응축이라는 단어가 조금 전문적으로 느껴질 것이다. 응축이라는 것은 말 그대로 뭉친다는 것이다. 그럼 보즈-아인슈타인 응축에서 보존은 정확히 무엇으로, 그리고 어떻게 뭉친다는 것일까?
보존들 사이에 상호작용이 전혀 없는 상황을 상상해 보자. 이러한 상황에서 개별 보존의 동역학을 기술하는 파동 함수를 \(\varphi({\bf r})\)이라고 하자. 그러면 \(N\) 개의 구별 불가능한 보존들로 이루어진 시스템의 동역학을 기술하는 다체 파동 함수는 개별 보존을 기술하는 파동 함수들의 단순 곱으로 쓸 수 있다.
$$\Psi_{\rm BEC}({\bf r}_1,{\bf r}_2,\cdots,{\bf r}_N)= \varphi({\bf r}_1) \varphi({\bf r}_2)\cdots\varphi({\bf r}_N)=\prod_{i=1}^N\varphi({\bf r}_i)$$
당연하게도 위 다체 파동 함수는 임의의 두 보존을 교환하는 것에 대해서 부호에 아무런 변화가 없다.
위 다체 파동 함수의 물리적 의미는 무엇일까?
모든 보존은 \(\varphi({\bf r})\)로 기술되는 단 하나의 상태로 존재한다. 그리고 전체 시스템을 기술하는 다체 파동 함수는 바로 이 단 하나의 파동 함수들의 곱으로 기술된다. 그런 의미에서 모든 보존은 하나의 상태로 뭉쳤다고 볼 수 있다. 특히 전체 시스템의 에너지는 항상 낮아지려고 하기 때문에 \(\varphi({\bf r})\)은 에너지가 가장 낮은 바닥 상태를 기술하는 파동 함수가 되어야 한다. 결국 모든 보존은 단 하나의 바닥 상태로 뭉치게 된다. 이것이 바로 보즈-아인슈타인 응축이다.
보즈-아인슈타인 응축은 실험적으로 어떻게 검증할 수 있을까?
커다란 퍼텐셜 우물에 갇힌 보존 시스템을 생각해 보자. (구체적으로 퍼텐셜 우물은 레이저로 만들 수 있다.) 보존 시스템이 보즈-아인슈타인 응축에 있다면, 모든 보존은 퍼텐셜 우물의 바닥 상태로 뭉치게 될 것이다. 이때 재미있게도 퍼텐셜 우물을 갑자기 없앨 수 있다면 보즈-아인슈타인 응축을 검증할 수 있다. 왜 그럴까?
만약 퍼텐셜 우물을 갑자기 없앤다면, 보존들은 자유롭게 사방으로 날아가기 시작할 것이다. 그런데 퍼텐셜 우물의 바닥 상태는 가장 정적으로 멈추어진 상태이다. 즉, 속도가 거의 없는 상태이다. 따라서 퍼텐셜 우물의 바닥 상태에 있었던, 즉 보즈-아인슈타인 응축으로 뭉쳐있었던 보존들은 시간이 지나도 움직이지 않고 거의 처음 위치 그대로 멈추어 있게 될 것이다. 이것이 기본적으로 2001년 에릭 코넬Eric Cornell, 칼 위만Carl Wieman, 울프강 케털리Wolfgang Ketterle가 노벨 물리학상을 수상하게 된 실험이다.
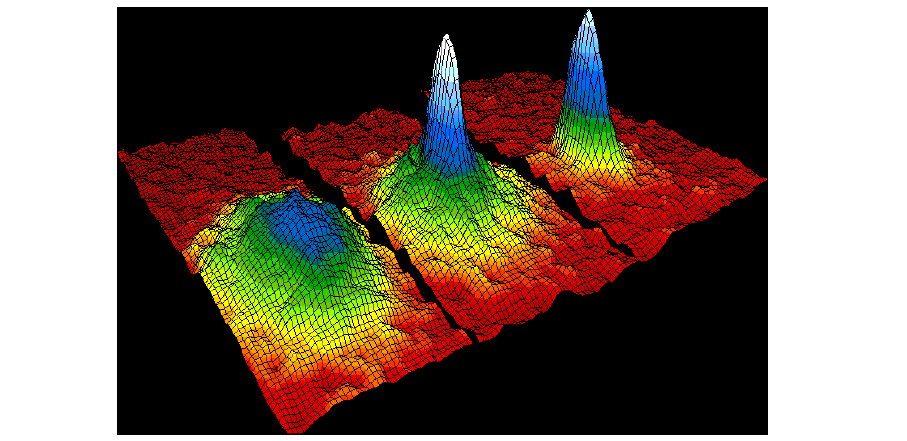
조금 더 구체적으로 [그림6]을 보자. 이 그림은 루비듐rubidium을 이용한 보즈-아인슈타인 응축 실험의 결과를 보여준다. 일단 [그림6] 안에는 3개의 세부 그림이 있다. 각 세부 그림에서 평면의 좌표는 파란색 혹은 흰색으로 표시된 부분을 기준 원점으로 삼을 때 퍼텐셜 우물을 없애고 일정 시간이 흐른 후에 루비듐이 도착하는 좌표를 나타낸다. 그런데 이 좌표는 잘 생각해 보면 퍼텐셜 우물을 없애기 전에 루비듐이 가졌던 \(x\)와 \(y\) 축 방향으로의 속도를 나타낸다고 볼 수 있다. 여기서 마치 낮은 언덕 혹은 높은 산처럼 보이는 높이는 각 좌표에 해당하는 속도를 가지는 루비듐의 개수이다.
그렇다면 각 세부 그림은 무엇을 나타내는 것일까?
보즈-아인슈타인 응축이 일어나기 위해서는 온도가 어떤 특정한 임계 온도critical temperature보다 낮아야 한다. [그림6] 속 3개의 세부 그림은 서로 다른 온도에 따라서 상황이 어떻게 바뀌는지를 보여준다. 즉, 왼쪽 그림은 온도가 임계 온도보다 높은 상황, 가운데 그림은 온도가 거의 임계 온도와 같은 상황, 오른쪽 그림은 온도가 임계 온도보다 낮은 상황을 보여 준다.
오른쪽 그림에서 보면 알 수 있듯이, 온도가 임계 온도보다 낮을 때 원점에서 높은 산이 불쑥 솟아오른다. 이것은 속도가 0에 가까운 루비듐의 개수가 급증한다는 것을 의미한다. 바로 보즈-아인슈타인 응축의 증거이다.
이제까지 설명한 내용만으로도 보즈-아인슈타인 응축이 노벨 물리학상이 수여될 만큼 흥미로운 현상임에는 의심의 여지가 없다. 하지만 아직 설명하지 않은, 어찌 보면 보즈-아인슈타인 응축의 가장 특별한 성질이 하나 남아있다.
사실 곧 아래에서 보겠지만 보즈-아인슈타인 응축이 특별한 이유는 모든 보존이 단 하나의 바닥 상태로 뭉치는 것뿐만 아니라, 이 바닥 상태를 기술하는 파동 함수의 위상도 모든 보존에 대해서 단 하나의 값으로 고정된다는 사실이다.
보통 파동 함수의 위상은 마음대로 바꿀 수 있다. 대신 물리적으로 의미있는 모든 측정 결과는 파동 함수의 위상에 상관없이 바뀌지 말아야 한다. 이 원리는 앞서 이미 여러 번 언급한 바 있는 게이지 대칭성이다.
그런데 보즈-아인슈타인 응축으로 뭉친 보존들은 모두 단 하나의 위상 값을 가진다. 말하자면, 게이지 대칭성이 깨지는 것이다. 그리고 게이지 대칭성이 깨지면 재미있는 일이 발생한다.
게이지 대칭성을 깨는 보존들은 아주 매우 자유롭게 흘러 다닐 수 있다. 여기서 어느 정도가 “아주 매우 자유롭게”인가가 중요한데, 보즈-아인슈타인 응축 상태에 있는 보존들은 전혀 아무런 저항 없이 자유롭게 흘러 다닐 수 있다. 잘 흐르는 물질을 보통 “유체fluid”라고 부르는데, 보즈-아인슈타인 응축 상태에 있는 보존들은 소위 “초유체superfluid”를 이룰 수 있다.
사실 초유체는 보즈-아인슈타인 응축이 실험적으로 검증되기 훨씬 이전에 발견되었다. 거칠게 말해서 앞서 설명한 보즈-아인슈타인 응축이 보존이 응축된 기체라면, 초유체는 보존이 응축된 액체이다. 초유체의 대표 물질은 바로 액체 헬륨이다.
헬륨은 보통 기체이다. 이러한 헬륨도 온도를 충분히 낮추면 액화된다. 엄밀하게 말해서 헬륨은 헬륨-4와 헬륨-3라는 2개의 동위 원소를 가지고 있다. 이 둘 중에서 보존인 헬륨-4가 어떤 임계 온도 이하로 액화될 때 초유체 현상이 나타난다. (사실 페르미온인 헬륨-3도 충분히 낮은 온도에서는 초유체 현상을 보인다. 퀴즈: 왜 그럴까?)
그런데 초유체 액체 헬륨-4의 행동 방식이 매우 특이하다. 초유체 액체 헬륨-4를 그릇에 담아 놓는다고 하자. 보통 액체는 그릇 안에 조용히 담겨 있을 것이다. 그릇은 액체의 흐름을 방해하는 하나의 장애물이다. 곰곰이 잘 생각해 보면 보통 액체가 그릇이라는 장애물을 뛰어넘지 못하는 이유는 액체와 그릇 표면 사이의 마찰력 때문이다. 물론 중력도 액체가 그릇 벽을 타고 올라가는 것을 방해할 것이다.
하지만 어떠한 장애물도 초유체 액체 헬륨-4의 흐름을 막을 수는 없다. 약간의 요동으로 조금이라도 움직이기 시작한 초유체는 그릇의 안쪽 벽을 타고 올라가 그릇 밖으로 흘러 나올 수 있다. 이렇게 그릇의 안쪽 벽을 타고 올라가기 위해서 생기는 얇은 초유체의 필름을 “롤린 필름Rollin film”이라고 부른다. 참고로, 중력의 효과는 롤린 필름의 두께(대강 30nm)가 충분히 얇아서 무시할 수 있다. 참고로 [그림7]을 보라.
[그림7]은 그릇에 담아놓은 초유체가 롤린 필름을 통해서 그릇의 안쪽 벽을 타고 올라서 밖으로 흘러나오는 상황을 보여준다. 혹시 그릇이 그보다 더 큰 상자 안에 있다면 밖으로 흘러나온 초유체는 상자의 안쪽 벽도 타고 오르기 시작할 것이다. 만약에 상자가 완벽하게 밀폐되어 있다면 상자의 천장까지 롤린 필름이 뒤덮게 될 것이다. 궁극적으로는 그릇에 담긴 초유체가 모두 밖으로 빠져나오게 되면 초유체의 흐름은 멈추게 된다.
초유체는 궁극적으로 보즈-아인슈타인 응축 현상이다.
그 이유는 다음과 같다. 보즈-아인슈타인 응축 상태에 있는 모든 보존은 단 하나의 상태로 존재한다. 단 하나의 상태가 가지는 가짓수는 물론 1이다. 따라서 보즈-아인슈타인 응축 상태는 엔트로피가 정확히 0인 상태이다. 따라서 보즈-아인슈타인 응축 상태에서 보존들은 아무런 무질서를 야기하지 않으면서 마치 한 덩어리처럼 흐를 수 있다.
다만 초유체 현상이 실제로 일어나기 위해서는 보즈-아인슈타인 응축 상태에 약간의 상호작용의 효과가 더해져야 한다. 그 이유는 개별 보존들이 보즈-아인슈타인 응축 상태를 이탈하는 것을 막아야 하기 때문이다. 비유적으로 말하자면 기체인 수증기에서 액체인 물로 바뀌어야 한다. 물 분자들 사이의 관계는 수증기보다 물에서 조금 더 “끈끈하다.”
조금 더 구체적으로 설명하면 다음과 같다. 아무리 보즈-아인슈타인 응축 상태에 속한 보존이라도 외부 장애물과 심하게 충돌하면 들뜸 상태excited state를 일으켜서 응축 상태를 이탈할 수 있다. 이러한 이탈을 막기 위해서는 보존이 웬만한 외부 자극에는 반응하지 않도록 해야 한다. 즉, 들뜸 상태가 잘 일어나지 않게 해야 한다. 초유체에서 에너지가 가장 적게 드는 들뜸 상태는 소리, 즉 음파sound wave이다. 따라서 외부 장애물이 음파를 발생시킬 정도로 큰 자극을 일으키지 않는 이상 초유체는 아무런 장애 없이 한 덩어리로 흐를 수 있다. 초유체를 형성하기에 액체가 유리한 이유는 기체보다는 액체에서 음파를 발생시키는 것에 에너지가 많이 들기 때문이다.
그런데 초유체와 매우 밀접하게 연결된, 하지만 더 신기한 현상이 있다. 바로 초전도체superconductor 현상이다. 초유체가 아무런 저항 없이 자유롭게 흐를 수 있는 유체라면, 초전도체는 전류가 전기 저항 없이 무한히 자유롭게 흐를 수 있는 도체이다. 즉, 원칙적으로 초전도체 안에서는 전류가 한 번 흐르기 시작하면 멈추지 않고 영원히 흐를 수 있다. 어떻게 이렇게 이상한 일이 발생할 수 있을까?
초전도체
초전도체는 1911년 네덜란드 레이던 대학교의 헤이케 카메를링 온네스Heike Kamerlingh Onnes에 의해서 처음 발견되었다. 온네스는 당시 본인이 개발한 헬륨의 액화 기술을 사용해서 다양한 물질이 저온에서 어떻게 행동하는지를 연구하고 있었다. 특히 온네스는 낮은 온도에서 수은의 전기 저항을 측정하고 있었는데, 절대 온도 4켈빈 근처에서 갑자기 전기 저항이 정확히 0으로 떨어지는 것을 발견하게 된다.
온도가 낮아질수록 열적 요동은 줄어든다. 따라서 낮은 온도에서 도체의 전기 저항이 줄어드는 것은 어찌 보면 매우 자연스러운 일이다. 하지만 전기 저항이 정확히 0이 되는 것은 아무리 생각해도 정말 놀라운 현상이었다. 무엇인가 굉장히 중요한 현상이 발견된 것이라는 공감대가 형성되었다. 그 결과 온네스는 불과 2년 뒤인 1913년 곧바로 노벨 물리학상을 수상한다.
하지만 이 놀라운 현상을 설명하는 것은 매우 어려웠다. 그도 그럴 것이 그 당시는 아직도 양자역학이 완벽하게 정립되기 전이었다. 슈뢰딩거 방정식은 1926년 처음 제안되었다는 것을 기억하라. 인류는 초전도체를 완벽하게 이해하기 위해서 1957년까지 46년을 더 기다려야 했다.
초전도체 현상은 믿기 힘들 만큼 이상하다. 이렇게 이상한 현상을 설명하기 위해서는 매우 창의적인 이론이 필요했다. 다행히 1957년 그러한 창의적인 이론이 탄생한다. 이 이론은 3명의 창시자들의 이름을 따서 바딘-쿠퍼-슈리퍼Bardeen-Cooper-Schrieffer, 줄여서 BCS 이론이라고 불린다.
(엄밀하게 말해서 초전도체 중에는 소위 “고온 초전도체”라고 불리는 임계 온도가 높은 초전도체가 있다. 불행히도 아직 고온 초전도체를 성공적으로 기술하는 이론은 없다. 만약 그러한 이론을 정립할 수 있다면 당신은 노벨 물리학상을 탈 수 있다. 가슴 뛰지 않는가?)
BCS 이론은 크게 두 부분으로 나뉜다. 즉, (1) 2개의 전자가 짝지어 하나의 쌍을 이루는 과정, 소위 짝짓기 메커니즘pairing mechanism에 관한 부분과 (2) 이러한 전자 쌍들이 뭉친 보즈-아인슈타인 응축 상태를 기술하는 다체 파동 함수, 즉 BCS 파동 함수에 관한 부분이다.
우선 BCS 이론의 첫 번째 부분에 대해서 이야기해 보자.
직관적으로 초전도체가 생기기 위해서는 전자들이 모종의 방법을 통해서 보존이 되어야 한다. 이러한 직관은 앞서 설명했듯이 초유체와 초전도체가 매우 유사하다는 실험적 사실에 근거한다. 전자들을 보존으로 바꾸는 방법은 생각보다 쉽다. 2개의 전자가 결합하여 하나의 쌍을 이루면 된다. 일반적으로 짝수 개의 페르미온이 결합하여 만들어진 결합 상태는 전체적으로 보존과 같이 행동하기 때문이다. (퀴즈: 왜 그럴까?) 이러한 전자의 쌍을 그 아이디어를 처음 제안한 물리학자 레온 쿠퍼Leon Cooper의 이름을 따서 “쿠퍼쌍Cooper pair”이라고 부른다.
아, 잠깐! 전자들끼리는 쿨롱 상호작용을 통해서 서로 강하게 밀어내지 않나? 물론 그렇다. 전자들을 서로 결합시키기 위해서는 쿨롱 상호작용과 다를 뿐만 아니라 그것을 넘어서는 특별한 결합 메커니즘이 필요하다.
결론부터 말하면 BCS 이론에 따르면 전자들은 고체의 뼈대를 이루고 있는 원자들의 배열, 즉 격자가 출렁거리기 때문에 서로 결합할 수 있다. 물리학자들이 흔히 표현하기를, 전자들은 격자가 출렁거려서 생기는 포논phonon을 서로 주고받으면서 끌어당길 수 있다.
이 말을 조금 더 쉽게 설명하면 다음과 같다. “믿기 힘든 양자 Incredible Quantum [11]: 양자 물질 상태”에서 배우기를, 고체는 거칠게 말해서 전체적으로 양의 전하를 지니고 있는 이온화된 원자들이 규칙적인 격자를 이루고 있고, 그 격자 구조 위에서 음의 전하를 지니는 전자들이 자유롭게 흘러 다니는 바다와 같다고 했다. 이러한 전자의 바다를 페르미 바다Fermi sea라고 한다. 페르미 바다에서는 전자 사이에 존재하던 쿨롱 상호작용의 효과가 마법 같이 사라진다.
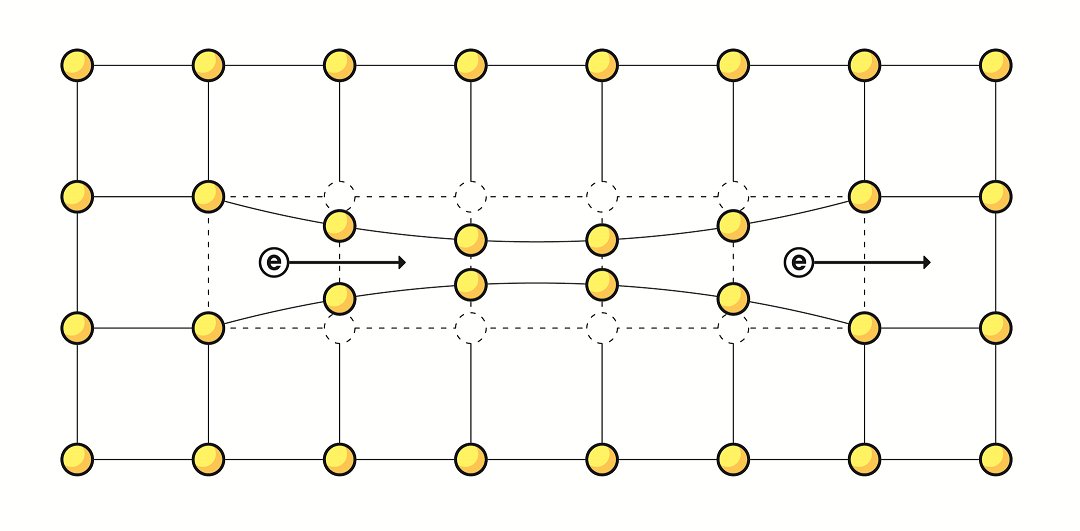
이 상황에서 어떤 주어진 전자가 격자 속에서 움직인다고 하자. 전자와 이온화된 원자는 서로 반대의 전기 전하를 지니기 때문에, 원자들의 격자 구조는 움직이는 전자의 주변으로 아주 미세하지만 찌그러지게 된다. 다만 전자는 가벼워서 빠르게 움직여 다닐 수 있는 반면, 원자는 무겁기 때문에 찌그러진 격자 부분은 빠르게 원상 복구되지 않는다. 여기서 중요한 점은 이렇게 찌그러진 격자 부분에는 다른 데보다 조금 더 많은 양의 전하들이 몰려 있게 된다는 것이다. 주변을 지나가던 다른 전자는 바로 이 부분에 끌리게 된다. 결과적으로 최초에 움직이는 전자와 그 주변을 지나가던 다른 전자는 찌그러진 격자 부분을 매개로 해서 유효적으로 서로 끌어당기는 힘을 느끼게 된다. 이 아주 미세하게 끌어당기는 힘이 바로 전자를 쿠퍼쌍으로 묶는 힘이다. [그림8]을 참조하라.
이제 BCS 이론의 두 번째 부분에 대해서 이야기해 보자.
구체적으로 BCS 이론의 두 번째 부분은 소위 BCS 파동 함수의 구축이다. BCS 파동 함수는 앞서 설명한 보즈-아인슈타인 응축 상태를 기술하는 다체 파동 함수 \(\Psi_{\rm BEC}\)와 매우 유사하게 쓰인다.
$$\Psi_{\rm BCS}={\cal A}\left[ \phi({\bf r}_1,{\bf r}_2) \phi({\bf r}_3,{\bf r}_4) \cdots \phi({\bf r}_{N-1},{\bf r}_N) \right]$$
위에서 \(\phi({\bf r}_i,{\bf r}_j)\)는 \(i\)와 \(j\)번째 전자로 이루어진 쿠퍼쌍을 기술하는 파동 함수이다. 보즈-아인슈타인 응축 상태를 기술하는 파동 함수인 \(\Psi_{\rm BEC}\)와 BCS 상태를 기술하는 파동 함수인 \(\Psi_{\rm BCS}\)가 유사한 점은 \(\Psi_{\rm BEC}\)가 개별 보존을 기술하는 파동 함수의 곱으로 쓰이는 것처럼 \(\Psi_{\rm BCS}\)도 기본적으로 개별 쿠퍼쌍을 기술하는 파동 함수의 곱으로 쓰인다는 것이다.
물론 다른 점도 있다. 구체적으로 쿠퍼쌍을 기술하는 파동 함수 \(\phi({\bf r}_i,{\bf r}_j)\)는 파울리의 배타 원리를 만족하기 위해서 \(i\)와 \(j\)번째 전자를 교환하는 것에 대해서 부호가 바뀌어야 한다.
$$\phi({\bf r}_j,{\bf r}_i)=-\phi({\bf r}_i,{\bf r}_j)$$
잠깐, 하나의 쿠퍼쌍을 구성하는 2개의 전자 사이에서는 위와 같이 파울리의 배타 원리를 만족시킨다고 하자. 그 외의 다른 전자들끼리는 어떻게 파울리의 배타 원리를 만족시킬 수 있을까?
이 문제를 해결하기 위해서 도입된 연산자가 바로 \({\cal A}\)라는 연산자이다. \({\cal A}\)는 BCS 파동 함수 \(\Psi_{\rm BCS}\)의 정의를 자세히 보면 맨 앞에 붙어있는 바로 그 연산자이다. 구체적으로 \({\cal A}\)는 \(N\)개의 총 전자 중에서 임의로 2개의 전자를 뽑아서 서로 교환하고, 그렇게 해서 얻어지는 새로운 파동 함수에 음의 부호를 붙인 후, 이러한 작업을 모든 가능한 경우에 반복하여 다 더하는 연산자이다. 전문적으로 \({\cal A}\)를 “반대칭화antisymmetrization 연산자”라고 부른다. 다시 한번 강조하지만, 반대칭화 연산자가 필요한 이유는 전체 파동 함수가 파울리의 배타 원리를 만족해야 하기 때문이다. 참고로 여기서 설명하기에 너무 기술적이라 자세히 들어가지는 않겠지만 \({\cal A}\)는 소위 “제2양자화second quantization” 방법을 쓰면 나름 쉽게 적용할 수 있다.
결론적으로 BCS 이론을 한마디로 정리하면 다음과 같다.
초전도체란 전자들이 쿠퍼쌍을 이루어 만들어진 보즈-아인슈타인 응축 상태이다.
다만, 아직 한 가지 확인할 사항이 남아있다. 쿠퍼쌍으로 이루어진 보즈-아인슈타인 응축 상태는 외부의 자극에 대하여 민감하게 반응하지 않을 것인가? 다행히 그렇다. 초전도체 상태의 들뜸 상태는 쿠퍼쌍이 깨진 상태이다. 따라서 외부의 자극이 쿠퍼쌍을 깰 정도로 세지 않다면 초전도체는 안정적으로 존재할 수 있다. 반대로 온도가 높으면 열적 요동으로 인해서 쿠퍼쌍들이 깨지기 시작한다. 특히 온도가 어떤 특정한 임계 온도보다 높아져서 모든 쿠퍼쌍들이 다 깨지게 되면, 초전도체 현상은 사라진다.
여기서 보즈-아인슈타인 응축 상태의 아주 특별한 성질을 다시 한번 기억해 보자. 바로 보즈-아인슈타인 응축으로 뭉친 보존들이 모두 단 하나의 위상 값을 가진다는 성질이다. 바로 게이지 대칭성이 깨진 것이다. 게이지 대칭성의 붕괴는 보즈-아인슈타인 응축 현상의 자연스러운 결과이다. 비슷하게 초전도체에서도 쿠퍼쌍들이 모두 단 하나의 위상 값을 가진다.
그런데 초유체와 다르게 초전도체에서의 게이지 대칭성 붕괴는 매우 놀라운 현상을 동반한다.
놀랍게도 빛이 무거워진다.
게이지 대칭성 붕괴: 힉스 메커니즘
사실 게이지 대칭성이 깨지면 아주 심각한 문제가 발생한다.
즉, 게이지 대칭성이 깨지면 입자의 개수가 일정하게 유지되지 않는다. 어찌 보면 질량 보존 법칙이 깨지는 것이다.
보즈-아인슈타인 응축에서 이 문제는 그리 심각한 문제로 드러나지 않았다. 거기에는 이유가 있다. 왜냐하면 보즈-아인슈타인 응축에 참여한 보존들과 그렇지 않은 보존들이 서로 개수를 약간씩 주고받을 수 있기 때문이다. 따라서 게이지 대칭성을 깨는 보존의 개수가 일정하게 유지되지 않는다고 하더라도, 전체 보존의 개수에는 변화가 없다. (약간 말장난을 하면 보존의 개수가 보존되지 않더라도 큰 문제가 없다.)
초전도체의 경우에도 쿠퍼쌍의 개수가 보존되지 않는다. 다만 이제는 문제가 조금 심각해진다. 그 이유는 쿠퍼쌍이 보통 전기 전하가 중성인 보존과 다르게 음의 전기 전하를 지니기 때문이다. 결과적으로 초전도체는 전하량 보존 법칙conservation law of electric charge을 위배하게 된다. 물론 이 문제도 초전도체에 참여하는 전자들과 그렇지 않은 전자들이 서로 개수를 약간씩 주고받는 것으로 해결될 수 있다.
하지만 쿠퍼쌍이 음의 전기 전하를 가진다는 사실은 초유체와 다르게 초전도체에서 매우 놀라운 현상을 야기한다. 다시 말해서 쿠퍼쌍은 음의 전기 전하를 지니기 때문에 빛과 상호작용하게 되는데, 바로 이 상호작용을 통해서 빛이 무거워질 수 있다.
이 현상의 이름은 “마이스너 효과Meissner effect”이다.
사실 마이스너 효과는 일반인들에서 훨씬 더 친숙한 다른 이름을 하나 가지고 있다. 그것은 자기 부상magnetic levitation 효과이다. 물론 자기 부상은 꼭 초전도체를 이용해서 구현할 필요는 없다. 요즈음 시중에서 많이 팔리고 있는 자기 부상하는 소품들은 전자기력을 복잡한 전자 제어 회로로 조절해서 자기 부상 효과를 구현한다. 자기 부상 열차도 초전도체를 이용해서 구현할 수도 있고, 전자적인 제어를 통해서 구현할 수도 있다.
본론으로 돌아가서, 마이스너 효과란 외부에서 걸어준 자기장이 초전도체의 내부로 파고 들어갈 수 없다는 효과이다. 이는 마치 초전도체의 내부에 외부 자기장을 상쇄시키는 모종의 전자석이 마법처럼 만들어지는 것과 같다. 예를 들어 초전도체 위에 자석을 올려놓으면 초전도체의 내부에 반대 극성을 가지는 전자석이 만들어져서 자석을 공중에 둥둥 띄우게 된다. 다름 아니라, 자기 부상 효과이다. 참고로 [그림9]를 보라.
이제 마이스너 효과를 구체적인 양자역학을 써서 유도해 보고자 한다.
우선 쿠퍼쌍을 마치 전자와 같이 하나의 근본적인 입자처럼 다룰 수 있다고 가정해 보자. 그렇다면 전자의 동역학을 기술하는 파동 함수가 존재하는 것처럼 쿠퍼쌍의 동역학을 기술하는 파동 함수도 존재하는 것이 매우 자연스러울 것이다. 그러한 파동 함수를 간단하게 \(\psi\)라고 표시해 보자. (전문적으로, \(\psi\)는 초전도 질서 함수superconducting order parameter라고 불린다.)
여기서 중요한 질문: 쿠퍼쌍의 동역학을 기술하는 파동 함수도 슈뢰딩거 방정식을 만족할까?
답: 아주 똑같지는 않지만 거의 비슷한 “유효 파동 방정식effective wave equation”을 만족한다. 구체적으로 유효 파동 방정식은 다음과 같이 쓰인다.
$$\frac{1}{2m^*}\left( -i\hbar\nabla-\frac{e^*}{c}{\bf A} \right)^2 \psi +a\psi+b|\psi|^2 \psi=0$$
위에서 \(m^*\)와 \(e^*\)는 각각 쿠퍼쌍의 질량과 전하이다. 여기서 \(a\)와 \(b\)가 구체적으로 어떤 값인지는 중요하지 않다. 전문적으로 위 유효 파동 방정식은 긴즈버그-란다우 방정식Ginzburg-Landau equation이라고 불린다.
긴즈버그-란다우 방정식은 슈뢰딩거 방정식은 아니지만 수학적으로 매우 유사한 구조를 지니고 있다. (사실 엄밀하게는 매우 큰 차이가 있다. 긴즈버그-란다우 방정식은 \(\psi\)에 대해서 비선형 미분 방정식non-linear differential equation이다. 반면에 슈뢰딩거 방정식은 물론 선형 미분 방정식이다.)
두 방정식 사이에 존재하는 수학적인 유사성은 매우 편리한 결과를 야기한다. 즉, “믿기 힘든 양자 Incredible Quantum [3]: 파동 방정식”에서 배운 바를 기억해 보면, 슈뢰딩거 방정식의 해가 연속 방정식continuity equation을 만족시켜야 한다는 조건으로부터 우리는 자연스럽게 “확률 분포의 흐름” \({\bf j}\)를 정의할 수 있었다. 이와 유사하게 여기서도 긴즈버그-란다우 방정식의 해가 연속 방정식을 만족시킨다는 조건을 통해서 다음과 같이 초전도체에서 흐르는 전류, 즉 초전류supercurrent를 정의할 수 있다.
$${\bf j}=\frac{e^*}{m^*}{\rm Re}\left[ \psi^* \left(-i\hbar\nabla-\frac{e^*}{c}{\bf A}\right) \psi \right]$$
여기서 \({\rm Re}[z]\)는 복소수 \(z\)의 실수 성분을 의미한다. 참고로 위 초전류 공식은 “믿기 힘든 양자 Incredible Quantum [3]: 파동 방정식”에서 유도한 공식에 두 가지 새로운 수정이 가해졌다. 우선 하나는 초전류를 나타내기 위해서 쿠퍼쌍의 전기 전하 \(e^*\)가 곱해졌다는 것이고, 다른 하나는 일반적으로 자기장이 걸린 상황을 기술하기 위해서 벡터 퍼텐셜의 효과가 고려되었다는 것이다. 참고로 초전류가 만족하는 연속 방정식은 다음과 같다.
$$\nabla\cdot{\bf j}=0$$
즉, 보통 전류이든 초전류이든 전류는 무에서 유로 저절로 샘솟지 않는다.
이제 초전류를 실제로 계산해 보자.
“믿기 힘든 양자” 시리즈를 통해서 꾸준히 강조하고 있듯이, 파동 함수는 일반적으로 복소수이다. 쿠퍼쌍을 기술하는 파동 함수도 마찬가지이다. 즉, \(\psi=|\psi|e^{i\theta}\)이다.
이제 파동 함수의 크기 \(|\psi|\)과 위상 \(\theta\)가 전류에 각각 어떤 역할을 하는지 알아보기 위해서 초전류 공식에 파동 함수를 집어넣고 정리하면 다음과 같다.
$${\bf j}=\frac{e^*}{m^*}|\psi|^2\left( \hbar\nabla\theta-\frac{e^*}{c}{\bf A} \right)$$
참고로 위 공식에서는 파동 함수의 크기 \(|\psi|\)이 공간에 대해서 일정하다는 가정을 썼다. 다시 말해서 쿠퍼쌍이 공간에 균질하게 퍼져있다고 가정해 보자.
이제 위상 \(\theta\)마저 상수로 고정된다면, 즉 \(\nabla\theta=0\)이 된다면 초전류는 다음과 같이 주어진다.
$${\bf j}=-\frac{(e^*)^2}{m^*c}|\psi|^2{\bf A}=-\frac{n_s(e^*)^2}{m^*c}{\bf A}$$
위에서 \(|\psi|^2\)은 쿠퍼쌍의 밀도 \(n_s\)로 치환되었다. 이 방정식은 초전도체 이론에서 매우 중요한 역할을 한 유명한 방정식이다. 바로 런던 방정식London equation이다.
기억하라. 위에서 우리는 아무리 여러 번 강조해도 지나침이 없을 정도로 중요한 초전도체의 성질을 하나 썼다. 그것은 초전도체에서 위상 \(\theta\)가 하나의 상수로 고정된다는 성질이다. 즉, 게이지 대칭성 붕괴라는 성질이다.
이제 런던 방정식의 양변에 컬curl 미분을 취하고 맥스웰의 방정식을 이용해서 약간 정리하면 다음과 같은 결론을 얻을 수 있다.
$$\nabla^2 {\bf B}=\frac{1}{\lambda^2}{\bf B}$$
여기서 소위 “런던 투과 깊이London penetration depth”라고 불리는 \(\lambda\)는 쿠퍼쌍의 밀도에 의존한다. (퀴즈: \(\lambda\)는 구체적으로 어떻게 표현되는가?)
위 미분 방정식은 적절한 경계 조건 하에서 쉽게 풀린다. 예를 들어서 \(x\)가 양수인 영역은 초전도체의 내부이고 음수인 영역은 \({\bf B}_0\)의 크기를 가지는 자기장이 걸린 초전도체의 외부라고 할 때, 위 미분 방정식의 해는 다음과 같이 얻어진다.
$${\bf B}={\bf B}_0 e^{-x/\lambda}$$
이 해는 외부 자기장이 런던 투과 깊이 정도까지만 초전도체의 내부로 들어갈 수 있다는 것을 의미한다.
곰곰이 잘 생각해 보면 이는 외부에서 주입된 자기장이 초전도체의 내부를 통과해서 진행하려는데 무거워져서 중간에 멈추는 것으로 해석될 수 있다. 더 나아가서 이는 자기장이 전자기장, 즉 빛의 일부임을 감안할 때 빛이 질량을 가지게 되는 것으로 해석될 수 있다.
물론 위 유도만 가지고는 빛이 정말 질량을 가지게 되는지에 대해서 확신이 서지 않을 것이다. 하지만 필자를 믿으라. 조금 더 정밀한 이론을 써서 분석해 보더라도 초전도체의 내부에서 빛은 정말 질량을 가지게 된다. 놀랍지 않은가?
그런데 잠깐, 아직 놀라기는 이르다. 더욱더 놀라운 사실이 우리를 기다리고 있기 때문이다.
초전도체의 내부에서 빛이 질량을 가진다는 사실은 그 자체로도 놀랍지만, 우리 우주의 운명을 좌우하는 매우 근본적인 원리를 품고 있다는 점에서 더욱더 놀랍다. 그 원리는 바로 힉스 메커니즘Higgs mechanism이다.
힉스 메커니즘은 원래 하나의 힘인 전자기약력electroweak force이 전자기력과 약력이라는 2개의 힘으로 갈라질 때 관여하는 원리이다. 앞선 “믿기 힘든 양자 Incredible Quantum [4]: 게이지 대칭성”에서 언급하기를 전자기력과 약력, 그리고 강력을 포함해서 세 가지 근본적인 힘은 모두 게이지 대칭성의 원리로 이해된다고 했다. 아직 완벽하게 정립되지는 않았지만, 많은 물리학자들은 중력마저도 궁극적으로 게이지 대칭성의 원리로 이해될 것이라고 믿고 있다.
이렇게 게이지 대칭성의 원리로 근본적인 힘을 이해하는 이론을 게이지 이론이라고 부른다. 구체적으로 게이지 이론에 따르면 전자기력은 광자를 주고받으면서 매개되고, 약력은 \(W^+, W^-, Z^0\) 보존이라는 세 종류의 게이지 보존을 주고받으면서 매개되며, 강력은 글루온gluon이라는 게이지 보존을 주고받으면서 매개된다.
그런데 사실 게이지 이론에는 매우 중대한 문제가 있다. 즉, 게이지 대칭성을 유지하기 위해서 게이지 보존은 원칙적으로 질량을 가질 수 없다!
광자는 질량이 없으므로 괜찮다. (물론 초전도체의 내부라는 특별한 상황을 제외하고 말이다.) 여기서 자세하게 설명할 수는 없지만, 글루온도 질량이 없다. 문제는 약력을 매개하는 게이지 보존들이다. 즉, \(W^+, W^-, Z^0\) 보존은 모두 질량을 가지고 있다. 그런데 앞서 말했듯이 게이지 보존은 원칙적으로 질량을 가질 수 없다. 게이지 보존이 질량을 가지려면 게이지 대칭성이 깨져야 한다. 그럼 어떻게 하면 게이지 대칭성을 붕괴시킬 수 있을까?
이 질문 어딘가 기시감이 들지 않는가?
앞서 설명하기를 초전도체에서 쿠퍼쌍으로 이루어진 보즈-아인슈타인 응축은 게이지 대칭성을 붕괴시킬 수 있다고 했다. 이렇게 게이지 대칭성을 붕괴시킨 쿠퍼쌍은 상호작용을 통해서 전자기력을 매개하는 게이지 보존인 광자에게 질량을 부여할 수 있다. 바로 마이스너 효과이다. 힉스 메커니즘은 이와 기본적으로 정확히 동일한 메커니즘이다. 즉, 힉스 보존Higgs boson이라는 모종의 입자가 보즈-아인슈타인 응축을 하고, 이렇게 게이지 대칭성을 붕괴시킨 힉스 보존이 상호작용을 통해서 \(W^+, W^-, Z^0\) 보존에게 질량을 부여할 수 있다.
놀랍지만 아직 끝이 아니다. 이즈음에서 더욱더 재미있는 일이 발생한다. 사실 \(W^+, W^-, Z^0\) 보존뿐만 아니라 우리가 아는 모든 페르미온의 질량도 궁극적으로 힉스 보존과의 상호작용을 통해서 발생한다. 결론적으로 보존과 페르미온을 망라하는 우리 우주의 모든 입자는 힉스 보존으로부터 질량을 얻는다.
사실 엄밀하게 말하면 힉스 보존이 모든 입자에게 질량을 부여한다는 것은 조금 과장이다. 예를 들어서 힉스 보존이 쿼크quark에게 질량을 부여하기는 하지만 실제로 양성자와 중성자를 포함한 중입자baryon의 질량의 거의 대부분은 그것을 구성하는 쿼크 자체의 질량이라기보다는 쿼크 사이의 상호작용 때문에 발생한다. 하지만 어쨌든 힉스 보존이 쿼크에게 질량을 주는 것은 사실이고, 쿼크가 애초에 질량을 가지지 않았다면 현재 우리가 아는 우주는 존재하지 않았을 확률이 크다.
참고로 [그림10]은 힉스 메커니즘을 제안한 공로로 피터 힉스Peter Higgs와 프랑수아 앙글레르François Englert에게 2013년 노벨 물리학상이 주어졌을 때, 힉스 메커니즘의 의미를 설명하는 삽화이다. 구체적으로 이 삽화는 힉스 보존이 근본적인 입자들을 하나로 묶어주는 핵심적인 퍼즐 조각이라는 사실을 표현한다.
그런데 곰곰이 잘 생각해 보면 이 지점에서 머리가 빙빙 돌아갈 정도로 아주 묘한 점을 발견할 수 있다. 게이지 대칭성의 붕괴는 우리 우주의 모든 입자에게 질량을 부여하는 원리이다. 그런데 묘하게도 게이지 대칭성은 우리 우주에 근본적인 힘이 존재할 수 있게 해 주는 원리이다. 한마디로 정리하면, 게이지 대칭성의 존재와 붕괴는 각각 우리 우주에 힘과 질량이 존재하도록 해 주는 것이다.
조금 더 근원적으로 가면 게이지 대칭성은 파동 함수가 위상을 가지기 때문에 발생한다. 따라서 우리 우주는 파동 함수가 복소수이기 때문에 존재할 수 있는 것이다.
다시 말해서 우리 우주는 양자역학 때문에 존재할 수 있다.
(참고로 앞에서도 이와 비슷한 말을 했다. “모든 새로운 질서는 양자역학 때문에 존재할 수 있다”라고…)
머리가 빙빙 돌아갈 정도로 묘하다는 필자의 말에 동의할 수 있지 않은가?
양자 이머전스
앞서 언급했듯이 필자의 전공 분야는 응집물질물리이다. 응집물질물리의 주요 연구 목표 중의 하나는 새로운 양자 물질의 발견과 탐구이다. 언뜻 스치고 지나갈 수 있지만, 여기서 중요한 단어는 “새로운”이다. 새로움이란 무엇일까?
사실 이 질문은 이 글의 초반부에서도 물어보았다. 구체적으로 필자는 이 글의 초반부에서 고체, 생명, 그리고 자유의지와 같은 새로운 질서는 어떻게 생길 수 있는가라는 질문을 했다. 우리는 그때 새로움이 정확히 무엇인지 구체적으로 정의하지 않았다. 예를 들어서, 자유의지가 우리 몸을 구성하는 개별 분자들의 물리화학적인 성질을 뛰어넘는 새로운 현상임이 너무나도 자명했기 때문이다.
자, 이제 물리학자의 관점에서 새로움을 구체적으로 정의해 보자.
“새로움이란 어떤 시스템을 구성하고 있는 부분에는 없던 성질이 전체 시스템의 집단 행동collective behavior으로 드러나는 모종의 성질이다.”
사실 새로움에 대한 위 정의는 인류 철학사에서 아주 오랜 역사를 가진다. 우선 고대 그리스 철학자인 아리스토텔레스Aristotle는 다음과 같은 명제를 남겼다.
“전체는 부분의 합보다 크다.”
“The whole is more than the sum of its parts.”
유명한 응집물질 물리학자인 필립 앤더슨Philip W. Anderson은 이 명제를 다음과 같은 시적인 표현으로 바꾸었다.
“많음은 다르다.”
“More is different.”
심지어 이런 관점에서 새로움을 정의하는 전문적인 철학적인 용어가 있다. 바로 영문으로 이머전스emergence, 국문으로 창발이라는 단어이다.
결론적으로 응집물질물리의 주요 연구 목표는 짧게 줄여서 양자 이머전스quantum emergence라고 할 수 있다.
양자 이머전스의 예는 짧게 언급하기에도 그 수가 너무 많다. 그리고 불행히도 흥미진진한 양자 이머전스 이야기를 더 하기에 이 글은 이미 너무 길다. 응집물질 물리학자로서 아쉽기는 하지만 이제 이 글을 마무리할 때가 되었다.
다만 필자의 전공 분야 중에서도 가장 최애 분야인 “분수 양자 홀 효과fractional quantum Hall effect”에 대해서는 아주 짧게라도 언급하고 이 글을 마무리하고 싶다.
앞서 양자 홀 효과를 설명할 때, 홀 전도도가 다음과 같이 양자화된다고 했다.
$$\sigma_H=\frac{e^2}{h} n$$
여기서 \(n\)은 얼마나 많은 란다우 준위가 전자들로 채워지는가를 나타낸다. 전문적으로 \(n\)은 채움 계수filling factor라고 불린다. 특히 앞선 설명에 따르면, 란다우 준위는 전자로 꽉 채워져야 하므로 \(n\)은 정수이어야만 한다. 실제로 양자 홀 효과를 만화로 설명할 때, \(n\)은 모종의 3차원 물체에 뚫린 구멍의 개수에 비유되었다. 구멍은 뚫리든지 뚫리지 않든지 둘 중 하나이지 0.5만큼 뚫릴 수는 없다. 참고로 이렇게 채움 계수가 정수인 양자 홀 효과를 “정수 양자 홀 효과integer quantum Hall effect”라고 부른다.
그런데 놀랍게도 1982년 미국 AT&T 벨 연구소의 물리학자였던 홀스트 스토머와 대니얼 추이는 분수로 양자화되는 양자 홀 효과를 발견한다. 이 현상이 바로 분수 양자 홀 효과이다. 분수 양자 홀 효과에서 홀 전도도는 다음과 같이 주어진다.
$$\sigma_H=\frac{e^2}{h} \nu$$
여기서 \(\nu\)은 위에서와 마찬가지로 채움 계수이지만, 다음과 같은 분수가 될 수 있다.
$$\nu=\frac{1}{3},\;\frac{2}{5},\;\frac{3}{7},\;\cdots,\;\frac{n}{2n+1}$$
다시 말해서 란다우 준위가 \(1/3\)만 채워져도, 즉 비유적으로 구멍이 \(1/3\)만 뚫려도 양자 홀 효과가 발생할 수 있는 것이다! (앞서 언급했듯이 스토머와 추이는 로플린과 함께 1998년 노벨 물리학상을 수상한다.)
도대체 어떻게 그럴 수 있을까?
여기서 어떻게 그럴 수 있는지 자세하게 설명하는 것은 불가능하다. 대신 재미있는 만화로 자세한 설명을 대신하고자 한다. 이 만화는 필자가 박사학위 과정 때, 정확하게는 1997년에 그렸다.
약간의 배경 설명을 하자면, 분수 양자 홀 효과는 필자의 박사학위 지도 교수인 제낸드라 제인Jainendra Jain 교수가 제안한 소위 “합성 페르미온composite fermion” 이론으로 설명된다. 필자는 어떤 계기로 합성 페르미온 이론을 설명하는 만화를 그리게 되었는데, 그 후로 이 만화는 꽤 유명해지게 되었다. 사실 양자 홀 효과를 연구하는 전 세계 많은 물리학자들은 필자는 몰라도 필자의 만화는 대부분 알고 있다.
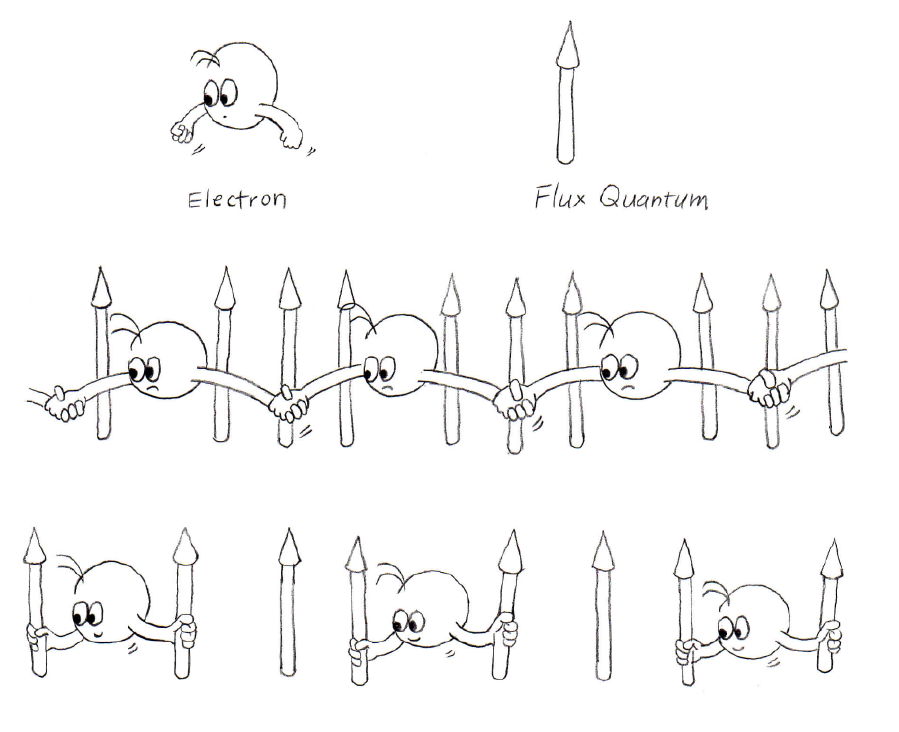
필자의 만화는 다음과 같다.
우선 [그림11]의 맨 위 칸을 보면, 큰 머리에 두 팔이 달린 “전자Electron”와 큰 화살표 모양의 막대기인 “자속 양자Flux Quantum”가 있다. 거칠게 말해서 자속 양자는 양자화된 자기장이다. 사실 자속 양자는 이미 이전에 한 번, 구체적으로는 “믿기 힘든 양자 Incredible Quantum [8]: 위상의 귀환”에서 설명한 적이 있다. 자속 양자는 그것이 담긴 솔레노이드의 주변을 전자가 한 바퀴 돌 때 전자의 파동 함수의 위상이 원래대로 돌아오는 자속의 세기를 나타낸다.
이제 [그림11]의 중간 칸을 보자. 전자들은 자속 양자들을 배경에 두고 서로 손을 잡으며 강하게 상호작용하고 있다. 참고로 자속 양자 1개당 전자의 개수가 바로 채움 계수이다. 따라서 여기서 채움 계수는 \(1/3\)이다. 이 상황에서 전자는 채움 계수가 \(1/3\)인 분수 양자 홀 효과를 만들어내야 한다. 어떻게?
답을 얻기 위해서 [그림11]의 아래 칸을 보자. 이제 전자들은 서로 손을 놓는 대신에 자속 양자를 2개씩 붙잡는다. 이렇게 전자 1개와 자속 양자 2개가 결합해서 만들어지는 새로운 입자가 바로 합성 페르미온이다. 우화적으로 말해서 전자들은 서로 강하게 상호작용하는 것이 싫다. 이에 전자들은 각자 자속 양자를 2개씩 붙잡아 합성 페르미온으로 변신하고 그제서야 자유를 즐기며 미소를 지을 수 있다. 그런데 전자에게 붙잡히지 않고 남아있는 자속 양자의 개수는 원래의 개수보다 줄어든다. 구체적으로 남아있는 자속 양자 1개당 합성 페르미온의 개수, 즉 유효 채움 계수는 이제 정수 1이다. 이 상황에서 합성 페르미온은 자기들만의 유효 채움 계수가 1인 정수 양자 홀 효과를 만들어내게 된다.
정리하면 분수 양자 홀 효과는 전자가 합성 페르미온이라는 새로운 입자로 변신하고, 이 새로운 입자가 유효적으로 정수 양자 홀 효과를 형성하는 것으로 이해할 수 있다.
전자로 이루어진 시스템에서 전자가 아닌 새로운 입자가 나타난 것이다.
이것은 양자 이머전스의 정수이다.