3월 퍼즐에 참여해주신 모든 분들께 감사드립니다!
3월의 퍼즐에 참여해주신 분 중 정답과 함께 좋은 풀이를 보내주신
김승기님께 문화상품권을 전달드릴 예정입니다.
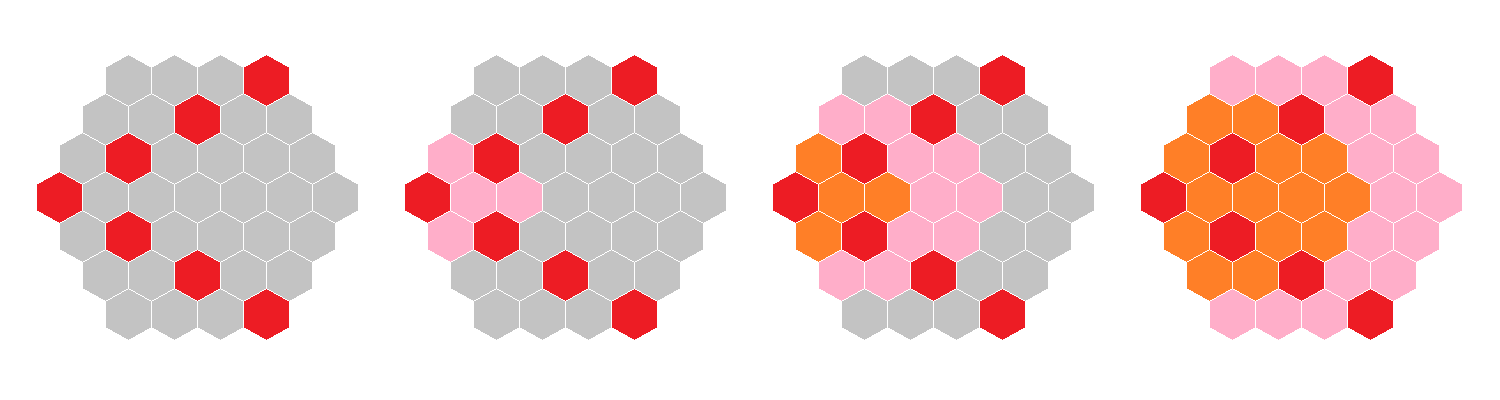
이 문제는 1986년 소련의 잡지 ‘KVANT’에 가장 먼저 소개되었다고 알려진 ‘The Infected Checkerboard’ 문제를 변형한 것이다. ‘시작 방’ \(2n-1\)개를 배치하는 방법은 여러 가지가 있는데, 다음은 그 중 하나이다.
\(n = 4\)의 경우를 예로 들면, 다음과 같은 절차로 내부에 크기 1, 2, 3, 4의 벌집을 순서대로 만들어 나가면 전체를 완성할 수 있다.
보너스 문제의 경우, 지어진 벌집의 둘레의 길이를 생각하면 간단하다. 문제에서 주어진 규칙 2번(주위를 둘러싼 6개의 공간 중에 3개 이상의 공간에 이미 방이 지어져 있는 자리에만 새 방을 지을 수 있다.)을 생각해 보면, ‘시작 방’들을 짓고 난 뒤에는 벌집을 지어 나가면서 둘레의 길이가 유지되거나 감소되는 수밖에 없다. 벌집을 1개 지을 때마다 기존 둘레에서 3, 4, 5, 6개의 벽이 사라지고 그 대신 각각 3, 2, 1, 0개의 벽이 새로 생겨 둘레가 되기 때문이다. 따라서 맨 처음 ‘시작 방’ 상태에서의 둘레의 길이가, 완성된 크기 \(n\)의 벌집의 둘레의 길이인 \(12n-6\)보다 크거나 같을 수밖에 없다. 최소한의 ‘시작 방’으로 둘레 \(12n-6\)을 만드는 방법은 방 \(2n-1\)개를 서로 떨어뜨려 지어 놓는 것이다. 따라서 ‘시작 방’은 \(2n-1\)개 이상일 수밖에 없다.
다음은 3월의 정답자로 선정된 김승기님의 해설입니다.