준결정의 수학: 펜로즈 타일링

우리 주변을 둘러보면 벽면이나 바닥을 아름답게 꾸민 타일링을 쉽게 볼 수 있습니다. 여기서 타일링이란 같은 모양의 타일을 이용하여 겹치지 않게 주어진 공간을 채우는 것을 의미합니다. 타일링의 다른 이름으로는 테셀레이션, 쪽매맞춤 등이 있습니다. 이 글에서는 준결정과 관련된 비주기적 타일링, 그중에서도 펜로즈 타일링을 수학적으로 어떻게 이해할 수 있는지 간단히 알아보려고 합니다.

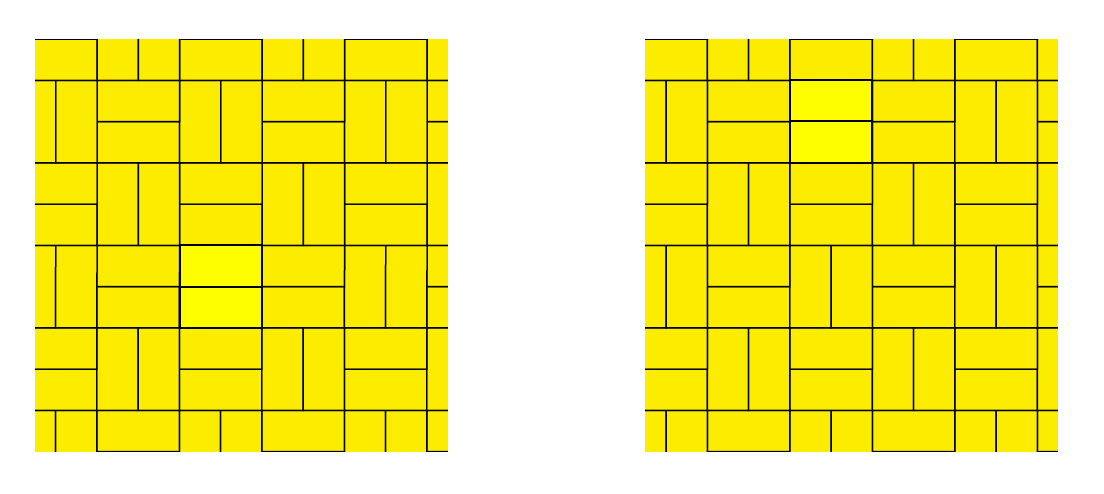
먼저 주기적 또는 비주기적 타일링이란 무엇인지 살펴보도록 하겠습니다. [그림1]처럼 직사각형 모양의 타일을 무한히 많이 이용하여 평면의 타일링을 만들어 보았습니다.

직사각형의 짧은 변의 길이를 1, 긴 변의 길이를 2라고 하면, 모든 타일을 위로 4만큼 평행이동하여 원래 타일링과 정확히 겹치는 (또는 일치하는) 타일링을 얻을 수 있습니다. 다른 방법으로 모든 타일을 오른쪽으로 4만큼 평행이동하여 정확히 겹치는 타일링을 얻을 수 있습니다. 이렇듯 모든 타일을 일정한 크기와 방향으로 평행이동하여 원래 타일링과 완전히 겹치는 타일링을 얻을 수 있다면, 이를 주기적 타일링이라고 합니다. 그럼 이번에는 [그림1]의 타일링에서 두 개의 타일의 위치를 바꾸어 [그림2]의 왼쪽과 같이 타일링을 만들어 보았습니다.

그럼, 처음에 가지고 있던 규칙성이 없어져서 모든 타일을 같은 크기와 방향으로 평행이동하여 정확히 겹치는 타일링을 얻을 수 없습니다. 예를 들어 모든 타일을 위로 4만큼 평행이동하면 [그림2]의 오른쪽과 같이 타일링을 얻게 되고 이는 원래 타일링과 거의 일치하지만, 정확히 일치하지는 않습니다.

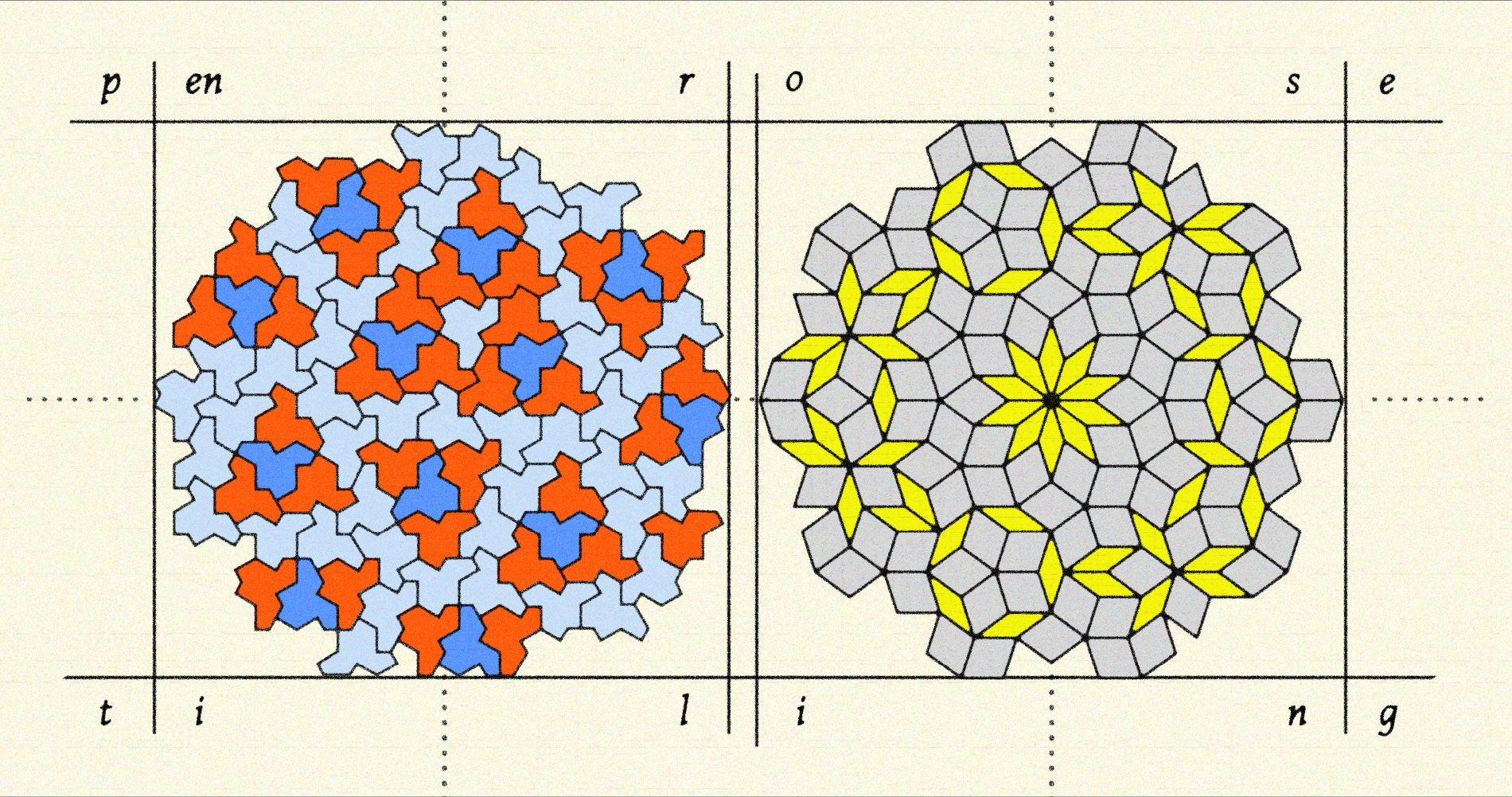
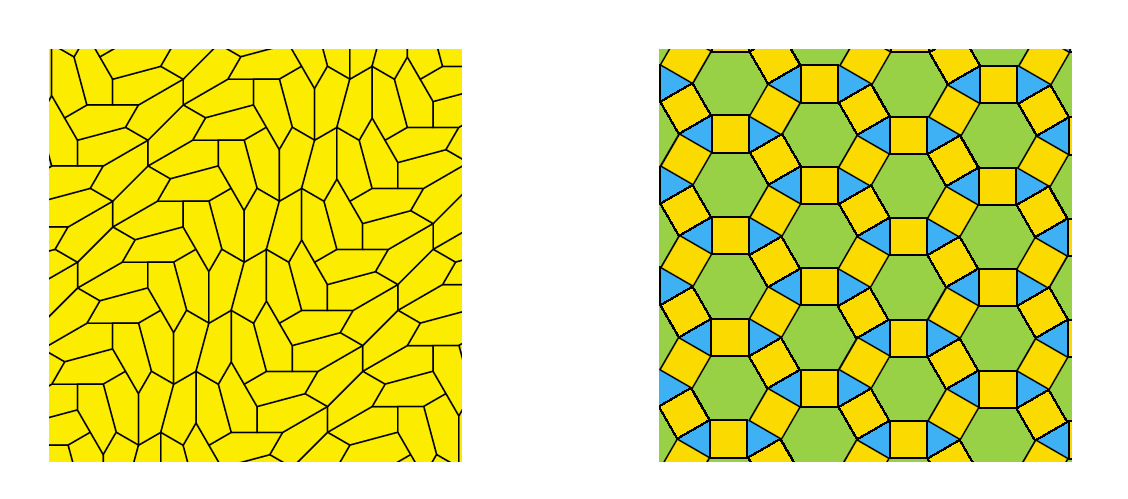
이렇듯 평형이동을 이용하여 원래 타일링과 정확히 겹치게 할 수 없다면, 이러한 타일링을 비주기적 타일링이라고 합니다. 따라서 변의 길이로 1과 2를 가지는 직사각형 타일을 이용하면 평면의 타일링을 얻을 수 있고, 이러한 타일링 중에는 비주기적 타일링뿐만 아니라 주기적 타일링도 있었습니다. 우리 주변에서 쉽게 볼 수 있는 타일링은 보통 주기적 타일링이고, 사각형뿐만 아니라 오각형 모양의 타일을 이용하여 [그림3]의 왼쪽과 같이 주기적 타일링을 만들 수 있습니다. 놀랍게도 이 타일링은 2018년에 처음 발견된 오각형 타일을 이용한 타일링입니다.[4] 물론 타일의 종류가 꼭 한 가지일 필요는 없습니다. [그림3]의 오른쪽과 같이 세 가지 종류(정삼각형, 정사각형, 정육각형)의 타일을 이용하여 타일링을 얻을 수도 있습니다.

그럼, 이 글에서 다룰 펜로즈 타일은 왜 흥미로울까요? 처음에 소개한 직사각형 타일을 이용하면 여러 가지 비주기적 타일링을 얻을 수 있지만, 주기적 타일링도 얻을 수 있습니다. 하지만 펜로즈 타일을 이용하면, 얻게 되는 모든 타일링이 항상 비주기적이라는 놀라운 성질을 만족하고, 이는 직사각형 타일과 펜로즈 타일이 근본적으로 다름을 의미합니다. 이렇듯 몇 종류의 타일이 주어져 있을 때 이를 이용하여 평면의 타일링을 얻을 수 있고 이러한 타일링이 모두 비주기적 타일링일 때, 이러한 타일(들의 모임)을 비주기적 타일이라고 부릅니다. 이렇게 놀라운 특징을 가지는 펜로즈 타일로부터 얻어지는 펜로즈 타일링에 숨어 있는 대수적 이론을 1981년 니콜라스 드 브루인^{Nicolaas Govert de Bruijn}이 발견하였습니다.[1] 

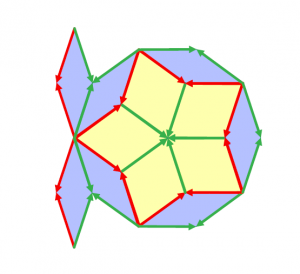
1974년 로저 펜로즈^{Roger Penrose}가 처음 발견한 펜로즈 타일링을 기술하는 방법에는 여러 가지가 있지만, 이 글에서는 마름모 두 개를 이용한 방법을 간단히 소개해 드리겠습니다.[6,7] [그림4]와 같이 \(72^\circ\)와 \(108^\circ\)를 각으로 갖는 두꺼운 마름모와 \(36^\circ\)와 \(144^\circ\)를 각으로 갖는 얇은 마름모를 생각합니다. 특히, 마름모가 가지는 변의 길이는 모두 같고, 녹색 화살표 또는 빨간색 화살표가 변에 주어져 있습니다.

이러한 두 개의 마름모 타일을 이용하여 [그림5]와 같이 화살표의 색깔과 방향이 일치하도록 평면을 채워 나아갑니다.

그러면 [그림6]과 같이 펜로즈 타일링을 만들 수 있고, 평면을 채우는 방법에 따라 서로 다른 무한히 많은 펜로즈 타일링을 얻을 수 있습니다. 또한 앞에서 언급했듯이 이러한 펜로즈 타일링은 항상 비주기적인 타일링이 됩니다!

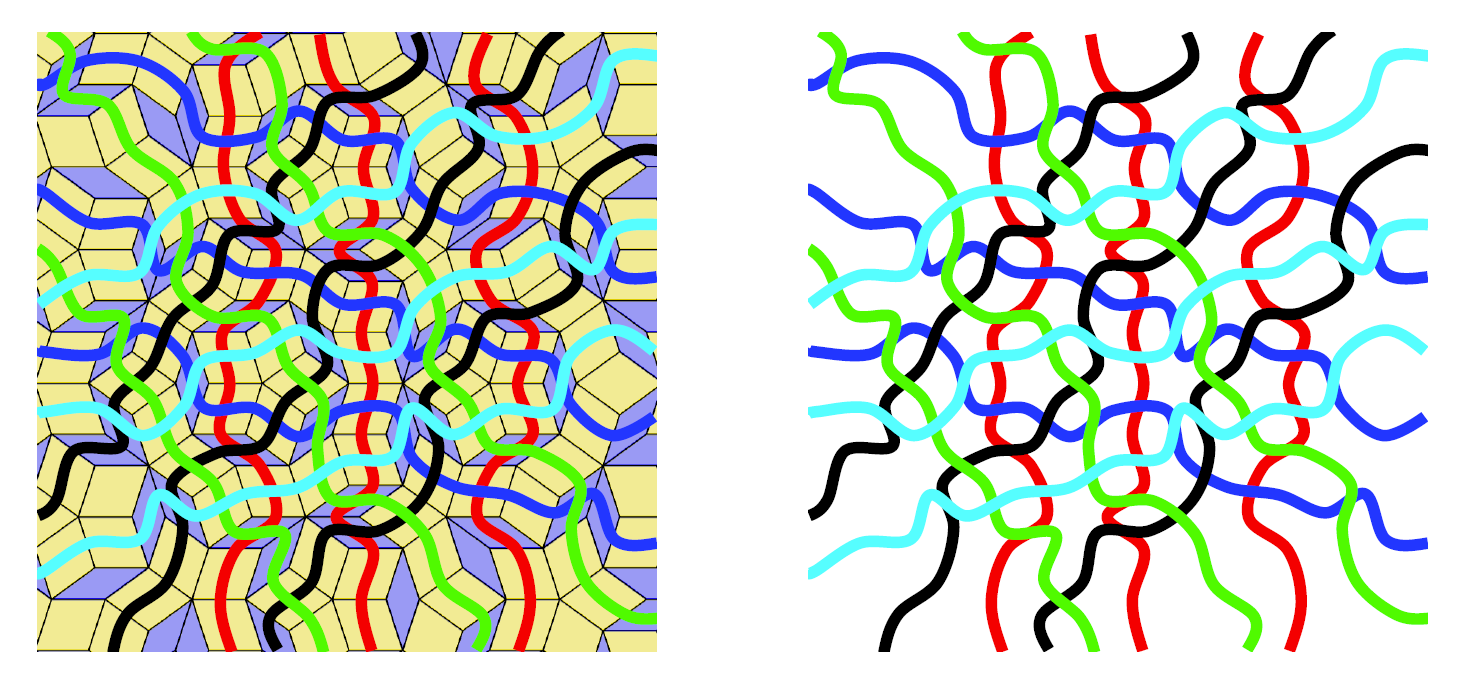
이러한 펜로즈 타일링을 대수적으로 이해하기 위해서는 펜로즈 타일링과 다섯평행줄과의 대응 관계를 살펴보아야 합니다. [그림7]에서와 같이 펜로즈 타일링에서 마름모의 한 변의 중점을 선택하고 마름모를 따라서 마주보는 다른 변의 중점을 연결하여 곡선을 만듭니다. 이때 서로 만나지 않은 곡선에 같은 색을 칠하면 다섯가지 색의 곡선들을 얻을 수 있습니다.

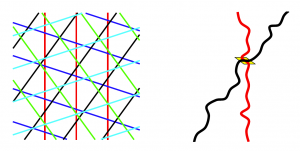
이때, 1만큼 떨어진 직선들을 모아놓은 집합을 하나의 평행줄이라고 하면, 앞에서 얻은 같은 색의 곡선들을 하나의 평행줄과 대응시킬 수 있습니다. 예를 들어, [그림8] 왼쪽의 빨간색 곡선들로부터 오른쪽의 빨간색 평행줄을 얻게 되는 것입니다.

이러한 평행줄 다섯개가 모여 [그림9]의 왼쪽과 같이 다섯평행줄를 이루게 됩니다. 이 때 주목할 점은 서로 다른 색을 가지는 두 곡선(또는 다섯평행줄의 서로 다른 색을 가지는 직선)의 교점은 마름모와 하나씩 대응이 됨을 알 수 있습니다. 이러한 대응이 니콜라스 드 브루인이 발견한 다섯평행줄과 펜로즈 타일링과의 관계를 대략적으로나마 이해할 수 있게 해 줍니다. 예를 들어, [그림9] 오른쪽의 빨간색 곡선과 검은색 곡선의 교점은 노란색 마름모 타일과 대응이 됩니다.

니콜라스 드 브루인는 이러한 다섯평행줄을 대수적으로 표현하고, 특별히 펜로즈 타일링이 하나의 복소수로 (거의) 결정됨을 보였습니다. 이로써 비주기적 타일링인 펜로즈 타일링에 대한 대수적 이론을 찾게 된 것입니다.

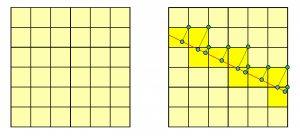
또한, 니콜라스 드 브루인는 펜로즈 타일링을 5차원 공간의 주기적 타일링으로부터 이해할 수 있다는 사실도 알아냈습니다. 이를 이해하기 위하여 먼저 2차원 공간의 타일로부터 1차원 공간의 타일을 어떻게 얻을 수 있는지 살펴보겠습니다. [그림10]의 왼쪽과 같이 길이가 1인 정사각형 타일로 2차원 공간의 타일링을 얻습니다. 그리고 2차원 공간에 1차원 평면(즉, 빨간색 직선)을 [그림10]의 오른쪽과 같이 선택합니다. 그럼, 정사각형 타일들 중에서 타일의 내부와 빨간색 직선이 만나는 타일의 오른쪽 위의 꼭지점(즉, 녹색 점)을 빨간색 직선에 수직으로 사영하면 빨간색 직선 위에 파란색 점들을 얻을 수 있습니다. 이러한 파란색 점을 1차원 다면체(즉, 선분)의 꼭지점으로 이해하면, 파란색 점을 꼭지점으로 가지는 선분으로 직선을 채우고 이로부터 타일링을 얻을 수 있는 것입니다.

앞의 설명과 비슷하게, 5차원 공간에 모서리의 길이가 모두 1인 큐브 모양의 타일을 생각할 수 있고 이를 이용하여 5차원 공간에 주기적 타일링을 얻을 수 있습니다. 여기서 큐브는 2차원 공간의 정사각형과 3차원 공간의 정육면체를 닮은 5차원 공간의 다면체로, 타일링을 이루는 큐브 모양의 타일들의 꼭지점은 5차원 공간의 좌표가 모두 정수인 점들의 집합이 될 것입니다. 이때, 5차원 공간 안에 2차원 평면을 잘 선택하면 이를 이용하여 펜로즈 타일링을 얻을 수 있습니다. 방법은 앞에서와 비슷하게 큐브 타일들 중에서 타일의 내부와 2차원 평면이 만나는 타일의 꼭지점 중에서 좌표가 가장 큰 꼭지점을 2차원 평면에 수직으로 사영하면 평면 위에 점들을 얻을 수 있고, 이러한 점들이 놀랍게도 펜로즈 타일링을 이루는 마름모 타일의 꼭지점이 된다는 것입니다.

이 글에서는 비주기적 타일링인 펜로즈 타일링과 다섯평행줄과의 관계를 포함하여 펜로즈 타일링에 숨겨진 수학에 대해 간단히 알아보았습니다. 마지막으로, 최근에 알려진 놀라운 소식을 전하며 이 글을 마칠까 합니다. 오랫동안 미해결 문제였던 한 개의 타일이 비주기적 타일이 될 수 있을지에 대한 질문을 2023년 3월에 David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Strauss가 해결하였다고 arXiv에 게시되었습니다.[8] 즉, [그림11] 같이 모자 모양의 13각형 타일로 얻은 타일링은 항상 비주기적 타일링이 된다고 합니다!