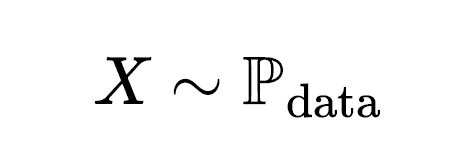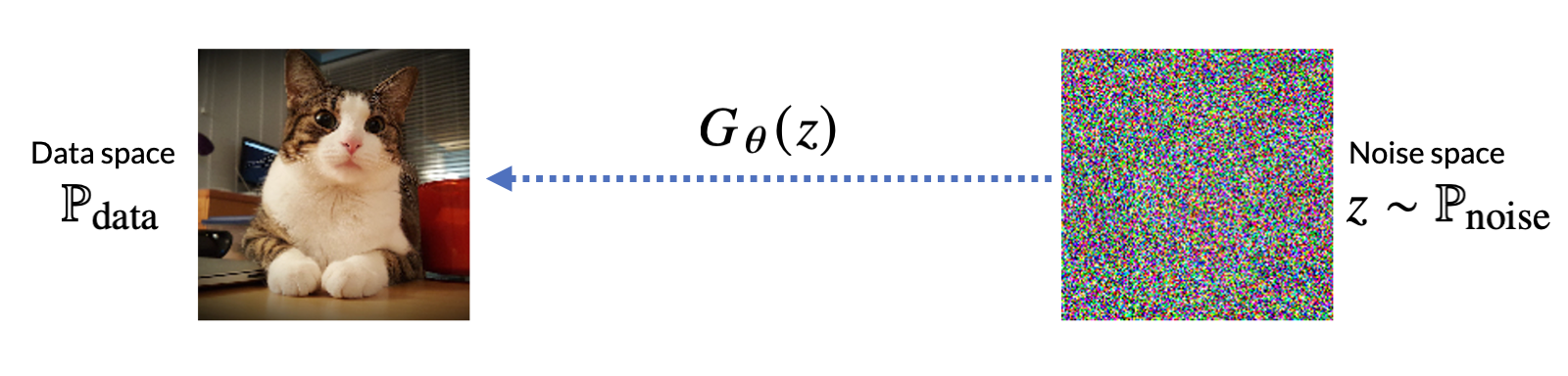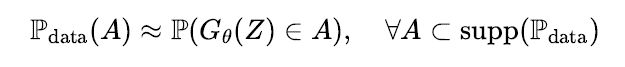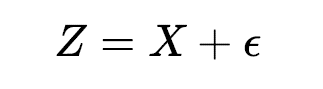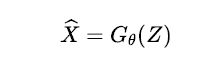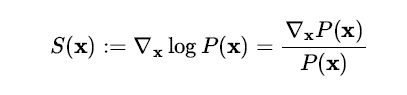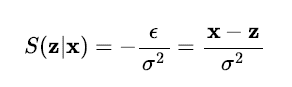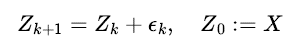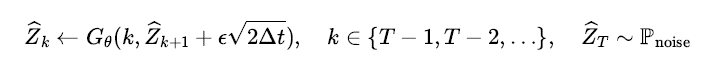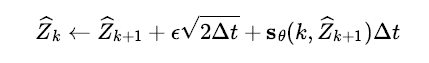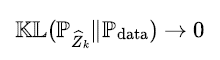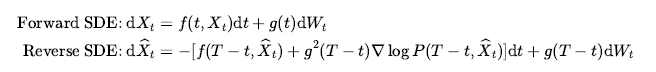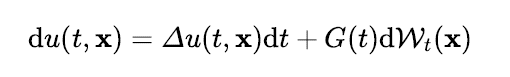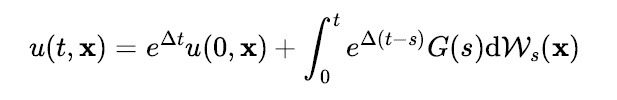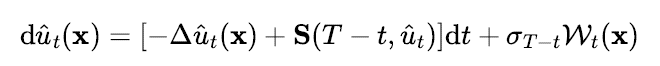확률편미분방정식과 인공지능

들어가는 글 – Generative AI의 시대

최근 주목 받고 있는 생성 인공지능(Generative AI)의 발전속도는 놀랍도록 빠르다.영상 데이터 뿐만 아니라 텍스트나 오디오 등 다양한 형태의 데이터를 고품질로 생성하는데 사용될 수 있다. 또한 텍스트를 입력으로 받아서 사용자가 원하는 형태의 영상이나 오디오를 출력하는 것도 가능하며, 로봇이나 게임 캐릭터의 모션까지도 자연스럽게 만들어내는게 가능하며 심지어 텍스트를 기반으로 편집도 가능하다.

맜살

자료1: 텍스트를 입력으로 받아서 생성한 영상 예제 (링크)
자료2: 텍스트를 입력으로 받아서 생성한 음성 예제 (링크)
자료3: 텍스트를 입력으로 받아서 생성한 모션 예제 (링크)
자료4: 텍스트로 모션을 편집하는 예제 (링크)

그렇다면 생성 인공지능의 핵심을 이루는 생성모델(Generative Model)은 어떤 원리를 기반으로 학습하고 동작할까? 그 전에 생성이란 바로 무엇일까? 통계학이나 기계학습 학문 분야에서 생성은 학습과정에서 관찰 또는 사용되지 않은 데이터를 데이터 공간 상의 확률분포 $\mathbb{P}_{data}$ 에서 샘플링 (sampling)하는 것으로 정의한다.

갑자기 확률분포와 샘플링이란 용어가 등장해서 혼동하는 독자들이 있을 것 같다. 여기서 말하는 샘플링은 주어진 데이터에서 고르는 과정이 아니라, 특정 확률분포를 따르도록 알고리즘을 통해 숫자를 만들어내는 과정을 뜻한다. 컴퓨터는 데이터를 숫자로 인식하고 출력한다. 우리가 모니터를 통해 보는 영상이나 텍스트는 컴퓨터가 출력한 숫자를 디코딩(decoding)하여 사람이 알아볼 수 있게 표현한 것이다. 인공지능이 실제 같은 영상이나 사람이 작성했을 법한 텍스트를 만들어낸다는 건, 생성 모델이 출력한 값들의 분포와 인코딩(encoding)된 실제 데이터들의 분포가 매우 유사한 패턴을 가져서 두 개를 통계적으로 구분하기 어려운 상태가 된 것이다.

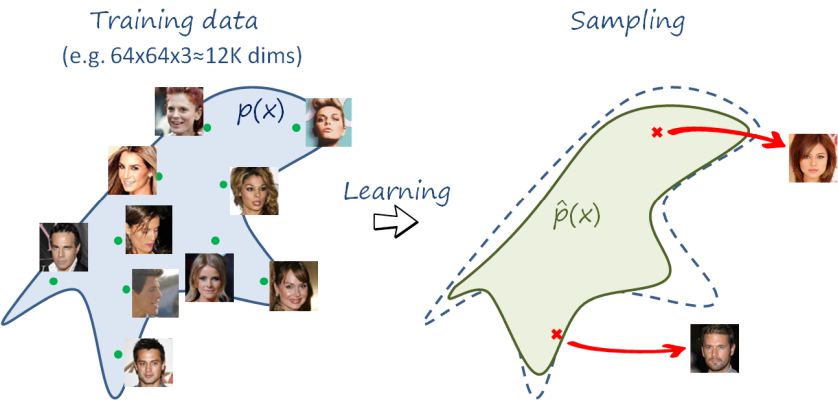
그림1: 생성 모델과 샘플링. 생성 모델의 목적은 데이터 분포에서 샘플링하는 것이다 (링크)

만일 데이터 분포 $\mathbb{P}_{data}$ 의 모양이 정규분포처럼 비교적 단순한 편이고 패러미터(parameter)도 알려져 있다면 샘플링은 크게 어렵지 않다. 그러나 영상이나 텍스트처럼 실제 데이터의 확률분포는 고차원 공간에서 표현되기 때문에 모양이 매우 복잡하다. 그러므로 샘플링할 때 유의미한 패러미터를 추정하는 작업이나 실제 데이터처럼 생성하는 것 모두 난이도가 높은 문제가 되고, 분포가 정의된 영역(support)에서 골고루 다양하게 샘플링하는 것은 훨씬 더 어려운 문제가 된다.

2014년에 공개된 GAN^[1] 의 등장 이후로 생성 모델 연구는 본격적인 주목을 받기 시작했는데, GAN은 생성 모델을 2인 게임이론에 기반하여 학습하는 발상에 착안하였다. 실제 데이터와 유사한 데이터를 생성해내는 생성자(Generator)와 두 데이터를 구분하는 판별자(Discriminator) 사이의 비협조 게임을 구성하고, 생성자와 판별자 사이의 반복적인 최소최대(min-max) 최적화 과정을 통해 생성 모델을 학습하는 방법을 제안하였다. GAN 이 생성해내는 영상은 품질이 매우 좋아서 인공지능 개발자들로부터 큰 주목을 받았는데, 아래 그림을 보면 7년 이라는 짧은 시간 동안 놀라운 속도로 발전이 이루어진 걸 볼 수 있다.

GAN은 훌륭한 생성 모델이지만 몇 가지 단점들을 가지고 있는데, 그 중 하나는 고품질의 데이터를 다양하게 샘플링하는 것이 어렵다는 점이고 (이를 fidelity-diversity tradeoff 라 한다), 다른 하나는 모델의 성능과 상관 없이 확률분포 $\mathbb{P}_{data}$ 의 모양이 어떻게 생겼는지 알기 어렵다는 점이다. GAN은 오로지 샘플링을 위한 방법론이기 때문에 확률분포 추정이 필요한 경우에는 다른 방법론을 사용해야 한다.

그렇다면 GAN 처럼 고품질의 데이터를 생성할 수 있으면서 확률분포의 추정도 가능한 생성 모델은 어떤게 있을까? GAN 과 비슷한 시기에 등장하여 생성 모델 연구자들이 주목해온 VAE(Variational AutoEncoder)^[2]나 Flow Model^[3] 들도 눈부시게 발전하였지만, 그 중에서도 혜성처럼 등장한 Diffusion Model 은 많은 인공지능 연구자 및 개발자들에게 큰 주목을 받고 있다. Stable Diffusion^[4] 이나 DALL-E^[5,6] 같이 Diffusion Model을 기반으로 생성 인공지능 서비스를 공개하는 업체들도 최근에 폭발적으로 생겨나고 있다.

그림4: 카카오브레인이 개발한 **Karlo** 가 생성한 이미지 (사진: 카카오브레인)

Part 1 – Diffusion Model 이해하기

본 글을 준비하면서 가장 고민이 깊었던 부분은 Diffusion Model 의 학습 원리를 소개할 때 Horizon의 어떤 독자들을 대상으로 상정할지였다. 고민 끝에 저자는 독자가 생성 인공지능 연구 분야에서 확률론과 통계적 기법이 어떻게 활용되는지 관심 있는 학부생 혹은 대학원 신입생이라 생각하고 작성하였다. 어떤 부분은 직관이란 이름으로 어물쩍 넘어가는 부분도 있을 것이다. 사실 Diffusion Model의 배경 지식을 제대로 이해하기 위해서는 확률론과 확률미분방정식 등 수학적 기초가 상당히 요구된다. 만일 해당 분야에 이미 지식이 충분한 독자들은 너그러운(?) 마음으로 Part1을 넘기기를 바란다.

Diffusion Model 의 학습원리는 무엇일까?

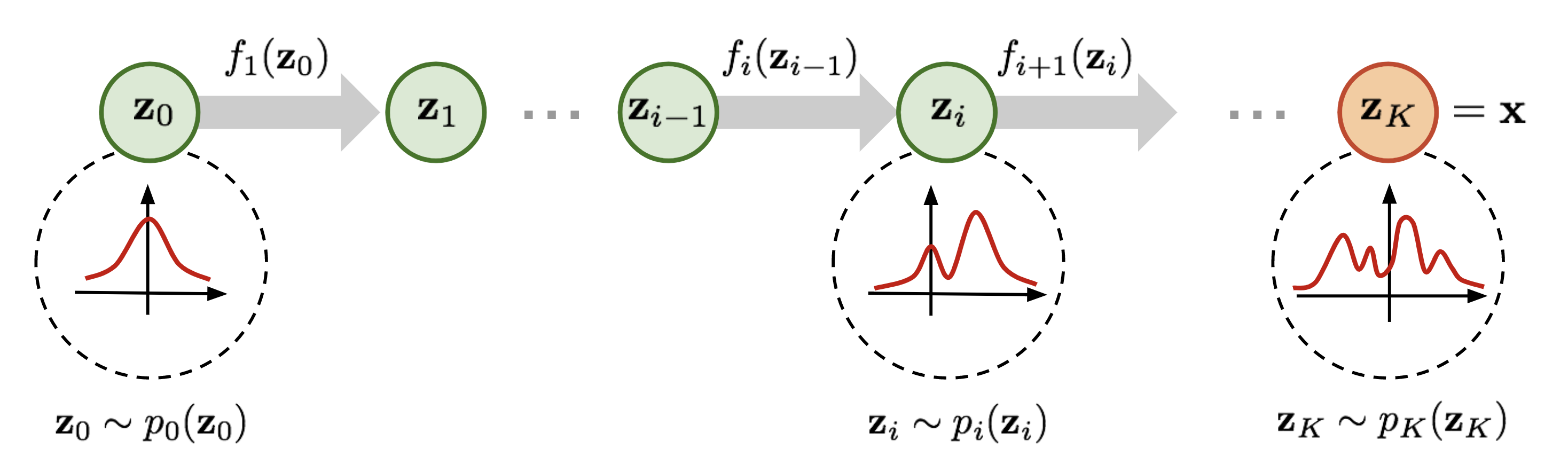
생성모델의 최종 목적은 들어가는 글 – Generative AI 의 시대 에서 설명했듯이 데이터 공간에 정의된 확률분포에서 데이터를 샘플링하는 것이다. 달리 말하면 노이즈 공간(noise space)에서 데이터 공간(dataspace)으로 매핑되는 기계학습 모델을 학습하는 것으로 이해할 수 있다. 확률론 용어로 더 풀어서 쓴다면, 노이즈 공간에 정의된 확률변수 $Z$ 를 데이터 공간에 정의된 데이터 분포 $\mathbb{P}_{data}$ 의 확률변수로 매핑시키는 함수 $G_{\theta}\left(Z\right)\sim$ $\mathbb{P}_{data}$ 를 찾고 싶은 것이다. 여기서 $\theta$ 는 기계학습 모델의 패러미터를 의미한다.

그림5: 노이즈 공간에서 데이터 공간으로 매핑되는 함수를 찾는 것이 생성모델 학습의 주 목표이다.

생성 문제에서 기계학습 모델이 만족해야할 성질은 다음과 같이 쓸 수 있을 것이다.

샘플링 된 데이터가 실제 데이터와 유사한 품질을 가져야 한다. 즉 모델을 통해 생성된 데이 터가 데이터 분포에서 실제로 관측 가능한 패턴으로 이루어져야 하는데, 이를 풀어서 쓰면 기계학습 모델의 출력이 데이터 분포의 서포트(support) 집합에 속할 확률이 높아야 한다 (주석: 간혹 다양체(manifold)라는 용어와 혼동해서 사용하는 논문들이 있는데, 이 경우는 서포트가 더 정확한 용어이다.).
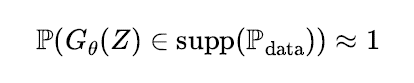
생성모델을 통해 데이터 공간의 전체 영역에서 골고루 샘플링이 가능해야 한다. 가령 노이즈 공간에서 확률변수를 무수히 많이 만들어서 기계학습 모델에 입력으로 넣었을 때, 출력 값들이 데이터 분포의 서포트 집합 대부분을 덮을 수 있어야 한다. 이걸 수식으로 풀어서 쓰면 $\mathbb{P}(\mathrm{supp}\left(\mathbb{P_{\mathrm{data}}}\right))$ \ $G_{\Theta}\left(\mathbf{\chi}_{noise}\right)$ 가 성립해야 하는데, 여기에 더하여 모드 붕괴(modecollapse) 문제가 발생하지 않아야 한다.

위의 두 가지 성질은 생성모델을 평가할 때 사용하는 척도인 정밀도(fidelity)와 다양성(diversity)과 관계가 있다. 만일 첫번째 조건이 만족되지 못한다면 생성모델이 생성해내는 데이터는 데이터 분포에서 샘플링했다고 말하기 어려울 것이다. 그러므로 생성모델의 정밀도가 떨어지면 샘플링을 위해 여러번 반복 생성해내는 작업이 필요하게 되고 체리피킹(cherry picking)을 위한 비용이 발생한다. 만일 두 번째 조건이 만족되지 못한다면 생성모델을 통해 샘플링할 수 있는 데이터가 일부 영역에만 제한적이고 기계학습 모델이 편향된 패턴이나 허위 상관(spurious correlation) 위주로 학습한다고 해석할 수 있다.

지난 10년 동안 기계학습 연구자들이 연구해온 GAN^[1] 이나 VAE^[2,3] 기반 생성모델들은 위의 조건들을 만족하는지 궁금한 독자들이 있을 것이다. 딥러닝 기반 생성모델 연구 속도가 워낙 빠르고 두 모델의 최신 연구 성과^[8,9,10]도 놀랍게 발전했기 때문에 단적으로 비교하는 것은 조심스럽다. 다만 기계학습 원리 측면에서 살펴보면 두 가지 성질을 동시에 만족시키는 건 상당히 난제이다. GAN의 경우 앞서 이미 설명했던 적대적 학습(adversarial training)을 통해 첫번째 조건이 만족되도록 생성모델 학습을 유도한다. 그러나 적대적 학습 방식은 생성모델이 데이터 공간 전체를 커버하면서 학습하는데 방해 요소가 되고, 결과적으로 모드 붕괴 문제를 야기하기 때문에 두번째 조건을 달성하는 것은 상당히 어렵게 된다. VAE의 경우 학습 데이터에서 추출한 특징 정보를 잠재공간(latent space) 상의 확률분포로 압축하는 인코(encoder)와 압축된 정보에서 데이터를 복원하는 디코더(decoder)를 활용해서 생성모델을 학습한다. 적대적 학습 방식과 달리 데이터 분포의 가능도(likelihood) 최적화를 이용하여 학습하기 때문에 두번째 조건을 만족하는 것이 가능하다. 그러나 압축된 잠재공간으로부터 영상처럼 고차원 데이터를 생성하는 방법을 디코더가 학습하려면 가능도 최적화 방식만으로는 한계가 있다^[8,9].

위에서 언급한 두 가지 조건들을 만족시키는 생성모델을 학습하려면 어떤 방법을 사용해야 할까? 본 글에서 소개할 Diffusion Model 은 다른 접근 방식으로 이 두 가지 문제를 해결한다. 먼저 데이터에 노이즈를 더하면 기존의 정보들이 일부 손상된 데이터를 만들어낼 수 있다.

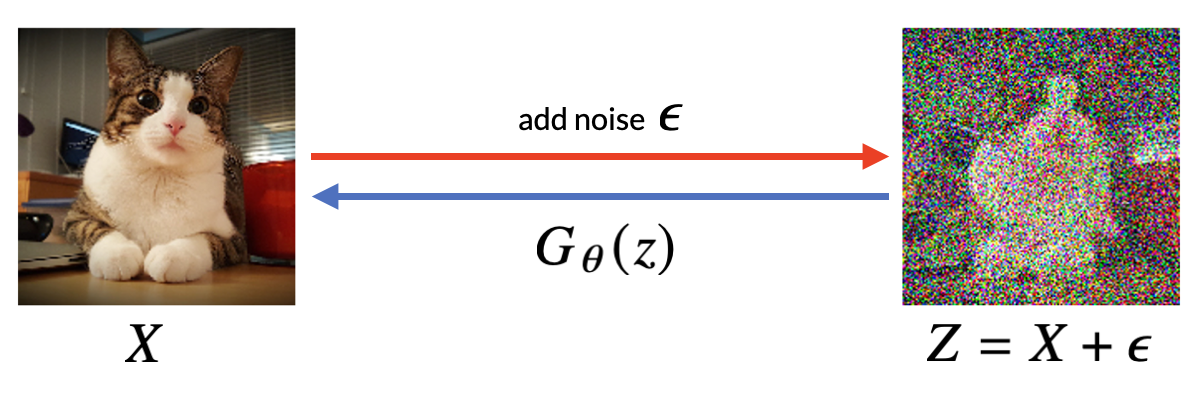
만일 손상된 데이터 $Z$ 로부터 원본 데이터 $X\mathbf{\mathbf{}}$ 를 복원하고 싶다면 노이즈 $\epsilon$ 의 크기가 얼마인지 추정해서 $Z$ 에서 빼주면 된다. 이걸 디노이즈(Denoise)라고 부르는데, 가령 아래 그림6 처럼 픽셀 별로 노이즈가 더해진 영상에서 어느 픽셀에 노이즈가 얼마나 삽입되어 있는지 추정하는 문제로 이해할 수 있다.

그림6: 노이즈가 더해진 영상에서 디노이즈를 수행하는 기계학습 모델

위의 그림6 처럼 노이즈가 더해진 데이터에서 디노이즈하는 방법을 학습한 기계학습 모델을 $G_{\theta}$ 라고 하자. 즉, 우리의 기계학습 모델은 원본 데이터에 노이즈가 더해진 데이터를 입력으로 받아 노이즈가 얼마나 더해졌는지 추정해서 새로운 영상 $\widehat{\mathrm{\mathit{X}}}$ 을 출력하는 모델이다.

그림 6처럼 데이터에 약한 노이즈가 더해지면 원본 데이터를 추정하는 것은 가능할 법 하지만, 더 강한 노이즈가 가해질수록 손상된 정보를 정확하게 추정하는 것은 어느 순간부터 어려운 문제가 된다. 그러나 우리의 목적은 생성(generation)이지, 기억(memorization)이 아니다. 따라서 학습 데이터에 존재했던 본래의 정보들을 모두 복원할 필요는 없고 (데이터 보안이나 프라이버시를 생각하면 오히려 더 문제가 될 수 있다!), 확률적인 변동성에 힘 입어 기존 데이터와 세부적인 모양은 다르지만 실제 데이터에서 보이는 패턴과 통계적으로 유사한 패턴들을 학습한 모델을 원한다. 이러한 아이디어에 착안한 방법론이 DAE(Denoising AutoEncoder)^[11,12]이다. DAE는 당시 Geoffrey Hinton 이 연구했던 RBM(Restricted Boltzmann Machine)^[13]을 대체하기 위해 고안된 기법인데, 노이즈 주입 과정을 통해 쉽게 손상되는(fragile) 정보들보다 데이터로부터 강건한(robust) 패턴들을 추출하도록 학습하게 되어 사전학습이나 비지도학습 등에서 유용하게 사용할 수 있다.

그렇다면 기계학습 모델은 디노이즈 과정을 통해 데이터 분포의 어떤 정보를 학습하게 되는 것일까? 흥미롭게도 DAE는 Aapo Hyvärinen 이 제안한 SM(Score Matching)^[14] 기법과 최적화 관점에서 동치라는 사실이 알려져있다 ^[15]. 여기서 Score 함수(주석: 통계학자 Charles M. Stein 의 이름을 기려서 Stein score 함수로도 부른다 ^[16,17])는 확률밀도함수의 로그에 대한 그레디언트 벡터로 정의한다.

SM 기법은 기계학습 모델이 데이터 분포의 Score 함수랑 매칭하도록 학습하는 목적식을 제안한다^[14]. 이 기법은 본래 정규화(normalization)가 어려운 통계 모형의 패러미터를 추정할 때 사용하는 기법으로, MCMC(Markov Chain Monte Carlo) 샘플링 기법이 가진 단점을 보완하기 위해 고안되었다. 그런데 위에서 소개한 디노이즈 과정을 SM 기법과 연결지을 수 있다. 가령 원본 데이터 $X\mathbf{\mathbf{}}$ 가 주어졌을 때 노이즈가 더해진 데이터 $Z$ 가 생성될 확률분포는 $P\left(\mathrm{z|x}\right)=P\left(\epsilon\right)$ 를 밀도함수로 가지게 된다. 만약 노이즈가 평균이 $\mathrm{O}\textbf{}$ 이고 분산이 $\sigma^{2}$ 인 Gaussian 분포를 따르게 된다면 이 조건부 확률분포의 Score 함수는 다음과 같이 계산된다.

기계학습 모델이 위의 조건부 확률분포의 Score 함수를 학습하도록 최적화가 진행되면, 노이즈가 더해진 데이터를 입력으로 받았을 때 주입된 노이즈의 크기가 분산에 비해 상대적으로 어느 정도 되는지 추정할 수 있게 되고, 손상된 정보 $Z$ 에서 원본 데이터인 $X\mathbf{\mathbf{}}$ 로 향하는 경로를 학습하게 된다. 이렇게 디노이즈 기반 SM 기법을 DSM(Denoising Score Matching)이라고 부르는데, Pascal Vincent 는 기존 SM 기법과 DSM 의 목적식이 동치이고, DSM과 DAE와 목적식이 또한 동치임을 증명한다 ^[15]. 즉, DAE 기법과 SM 기법은 동치인 목적식을 가지기 때문에 최적화를 수행했을 때 결과적으로 동일한 패러미터를 얻게 된다. 결론적으로 디노이즈 과정을 통해 기계학습 모델은 데이터 분포의 Score 함수 정보를 학습하게 된다.

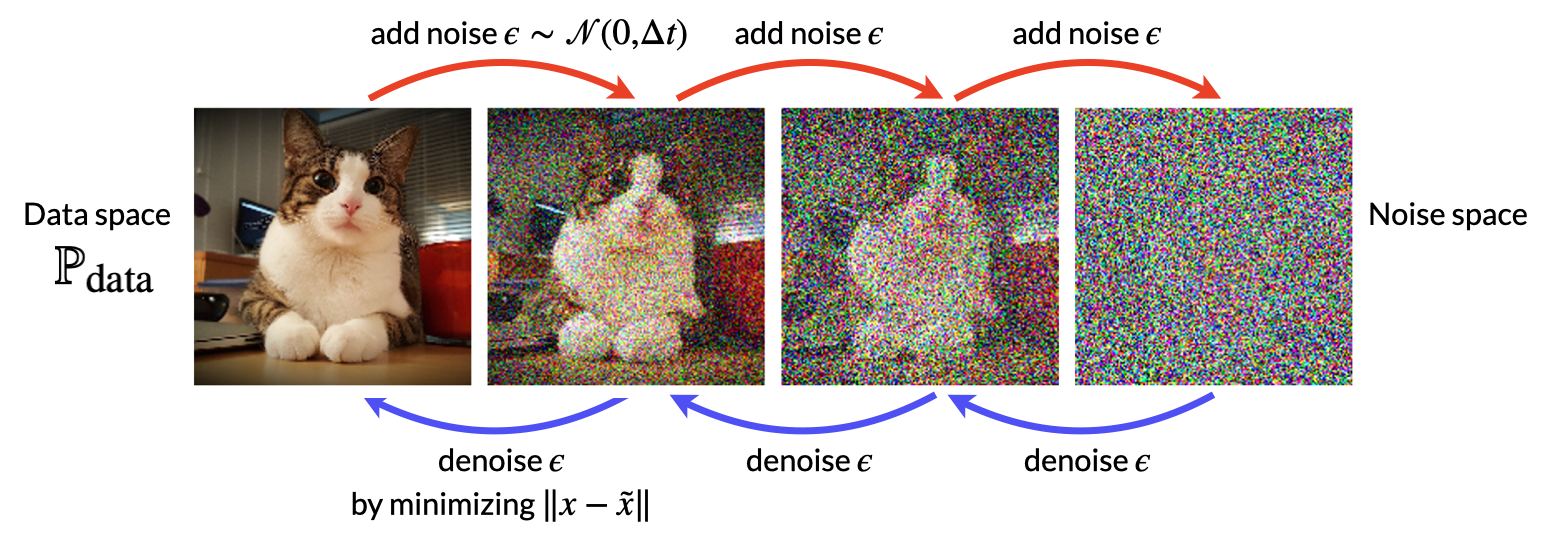
위에서 소개한 디노이즈 방식으로 학습할 수 있는 패턴들은 생성모델로 하여금 데이터 분포를 모사하는데 도움은 되지만, 노이즈 공간에서 바로 고품질의 데이터를 생성하기에는 한계가 있다. 왜냐하면 원본 데이터의 정보가 완전히 사라진 상태에서는 디노이즈를 학습한 모델의 출력도 노이즈랑 별반 차이가 없기 때문이다. 그렇다면 노이즈를 점진적으로 바꿔가면서 더해주고, 각 과정마다 디노이즈하는 모델을 학습해서 사용하면 어떨까? 그림7 처럼 노이즈 주입과 디노이즈 과정을 단계 별로 나눠서 생성 모델의 학습 원리로 사용하는 것이 바로 Diffusion Model 의 핵심 아이디어다. 여러 기계학습 연구자들이 비슷한 아이디어를 제시했지만, 영상 생성 분야에서 성공적인 학습 결과를 선보인 논문은 Ho et al. 이 제안한 방법론이 DDPM(Denoising Diffusion Probabilistic Model)^[18]이다. Diffusion Model 의 이론적인 원형이 궁금한 독자는 Sohl-Dickstein et al. ^[19] 논문도 같이 보는 것을 추천한다.

그림7: 데이터에 노이즈를 더하는 과정(순방향) vs 디노이즈하는 과정(역방향)

Diffusion Model 은 확률미분방정식의 해를 근사한다

디노이즈를 학습하는 생성모델과 확률미분방정식은 어떤 관련이 있을까? 학습 데이터에 분산의 크기를 $\Delta\mathrm{t}$ 만큼 제어한 Gaussian 노이즈 $\epsilon _{k}\sim N\left(0,\Lambda\mathrm{t}\right)$ 를 순차적으로 더해보자.

각 시점에서 주입한 노이즈를 $Z\mathrm{}_{k+1}$ 로부터 추정해서 디노이즈를 학습한 기계학습 모델 $G_{\Theta}\left(k,Z_{k+1}\right)\approx Z_{k}$ 을 가정해보자. 디노이즈 모델을 가지고 샘플링을 하려면 그림 7에서 보듯이 마치 시간 여행자처럼 종착지인 노이즈 공간에서 출발하여 시작 지점인 데이터 공간에 도달할 될 때까지 역순으로 디노이즈가 수행되어야 한다. Diffusion Model 은 이 과정에서 확률적 변동성을 부여하기 위해 매 시점마다 디노이즈 모델이 출력한 값에 $\epsilon\sqrt{2\Delta t}$ 만큼 Gaussian 노이즈를 더해서 다음 순서의 입력으로 사용한다(주석: 이 새로운 노이즈를 주입하는 과정 없어도 $G_{\theta}$ 학습이 잘 되었다면 샘플링 알고리즘은 동작 가능하며, 초기 난수를 동일하게 입력하면 모델의 출력도 동일하게 된다. 이 부분도 흥미로운 주제지만 본 글에서는 자세한 설명을 생략한다. 궁금한 사람은 Song et al. ^[21] 논문에서 Probability Flow ODE 를 찾아보자.).

위에서 디노이즈를 학습하는 생성모델은 조건부 확률분포의 Score 함수를 학습하는 DSM 기법과 동치인 목적식을 가진다고 설명하였다. DSM 기법을 통해 학습하는 기계학습 모델을 Score 모델이라 부르는데, 이 모델을 $\mathbf{s}_{\theta}$ 로 표기하자. 디노이즈 모델과 Score 모델 사이의 관계를 이용하면 위 수식을 다음과 같이 Euler-Maruyama 근사식의 형태의 정리할 수 있다.

여기서 DSM 기법과 SM 기법의 동치성을 이용하면 Score 모델이 학습을 통해 최종적으로 근사하게 될 대상은 데이터 분포의 Score 함수인 $S(x)=\bigtriangledown\mathrm{log}P(\mathrm{x})$ 와 같게 된다. 결론적으로 Diffusion Model 의 샘플링 알고리즘은 확률미분방정식인 Langevin 방정식의 수치적 해를 구하는 LMC(Langevin Monte Carlo) 알고리즘을 근사하게 된다!

LMC 알고리즘을 통해 순차적으로 샘플링되는 확률분포는 특정 조건을 만족하면 $\Delta t$ 와 $k$ 가 0 에 다가갈수록 데이터 분포와 가까워진다 [20]. 가령 분포 사이의 거리를 KL 발산(Kullback-Leibler divergence)으로 계산하면 Diffusion Model 에서 사용하는 목적식은 아래와 같은 분포의 수렴을 추구하게 된다.

실제로 데이터 분포에 특정 조건을 부여하면 위 수렴이 충족된다는 걸 이론적으로 보일 수 있다^[21] (주석: 만약 데이터 공간이 저차원 다양체 위에 존재한다면(manifold hypothesis) KL 발산 대신 Wasserstein 거리함수로 바뀌게 된다 ^[22]). 이를 통해 앞서 살펴본 생성 모델이 만족해야할 두 가지 성질, 정밀도와 다양성을 자연스럽게 유도하게 된다. 만일 데이터 분포의 서포트 밖에서 $\widehat{Z}_{k}$ 가 반복적으로 샘플링 된다면 KL 발산 값은 무한대가 되어 버리므로 위의 조건과 상충된다. 따라서 샘플링 알고리즘이 순차적으로 진행될수록 데이터 분포의 서포트 바깥에서 생성될 확률이 0 으로 수렴해서 정밀도가 보장된다. 또한 $\mathbb{P}_{\widehat{Z}_{k}}$ 는 샘플링 과정에서 더해지는 확률적 변동성에 의해 데이터 분포의 서포트 내부에서는 $\mathrm{O}$ 보다 큰 확률 값을 가져야 한다. 그러므로 위의 조건이 충족되려면 $\mathbb{P}_{\widehat{Z}_{k}}$ $\neq\mathbb{P}_{\mathrm{data}}$ 인 영역의 크기가 감소해야 하고, 이는 결과적으로 다양성을 보장하도록 학습이 진행된다는 의미이다. 종합하면 Diffusion Model 학습 방식은 실제 데이터와 유사한 품질을 가지면서 동시에 데이터 분포가 정의된 영역에서 골고루 샘플링 하도록 유도하게 된다.

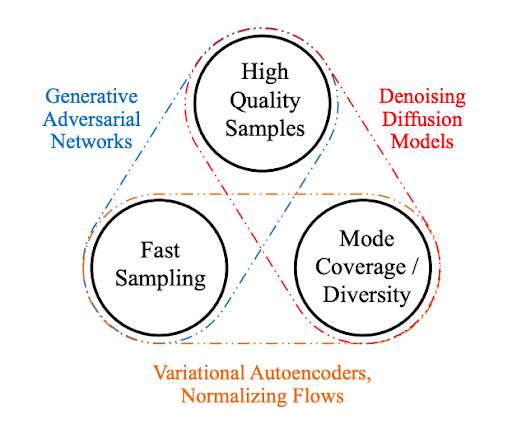
그림8: 생성모델 GAN, VAE, Diffusion Model 간 비교 (출처: Nvidia, 링크)

지금까지 Diffusion Model 의 기본적인 학습 원리와 Langevin 확률미분방정식 사이의 연결고리를 설명하였고, 이를 통해 생성모델로서 Diffusion Model 이 가지게 되는 장점도 살펴보았다. 사실 고품질의 데이터를 다양하게 생성하기 위해서는 확률미분방정식 이론만으로는 보장하기 어려운 추가적인 공학적 접근들이 필요하다. 이런 부분들이 궁금한 독자는 LDM(Latent Diffusion Model)^[4] 이나 Guided Diffusion^[7] 논문들을 읽는 걸 추천한다.

Part 2 – Score 기반 생성모델과 확률편미분방정식

Diffusion Model 의 학습 및 생성 원리는 데이터 분포와 노이즈 분포 사이의 변환과 역변환을 여러층을 거쳐 모델링하는 Flow Model 과 닮은 부분이 많다. 차이가 있다면 Flow Model 은 층 사이의 변환을 결정론적(deterministic) 함수로 학습하고, 이 함수를 통해 노이즈 분포에서 뽑힌 무작위 값을 데이터 분포가 정의된 공간으로 보내서 데이터를 생성한다. 두 생성모델 모두 가역적(reversible)인 변환을 이용하여 데이터 분포에서 샘플링하려는 목적은 유사하지만, 결정론적 함수와 확률과정에서 사용하는 가역적인 변환의 의미와 용도는 다소 다르다. 결정론적 함수의 경우 입력과 출력 사이의 역(inverse)변환이 잘 정의되어야 하므로 일대일대응(bijective) 조건이 요구된다. 따라서 Flow Model 에서 각 층마다 사용할 수 있는 함수의 형태는 상대적으로 제한적일 수 밖에 없다.

그림9: Flow Model 과 Diffusion Model 의 샘플링 과정 비교 (링크)

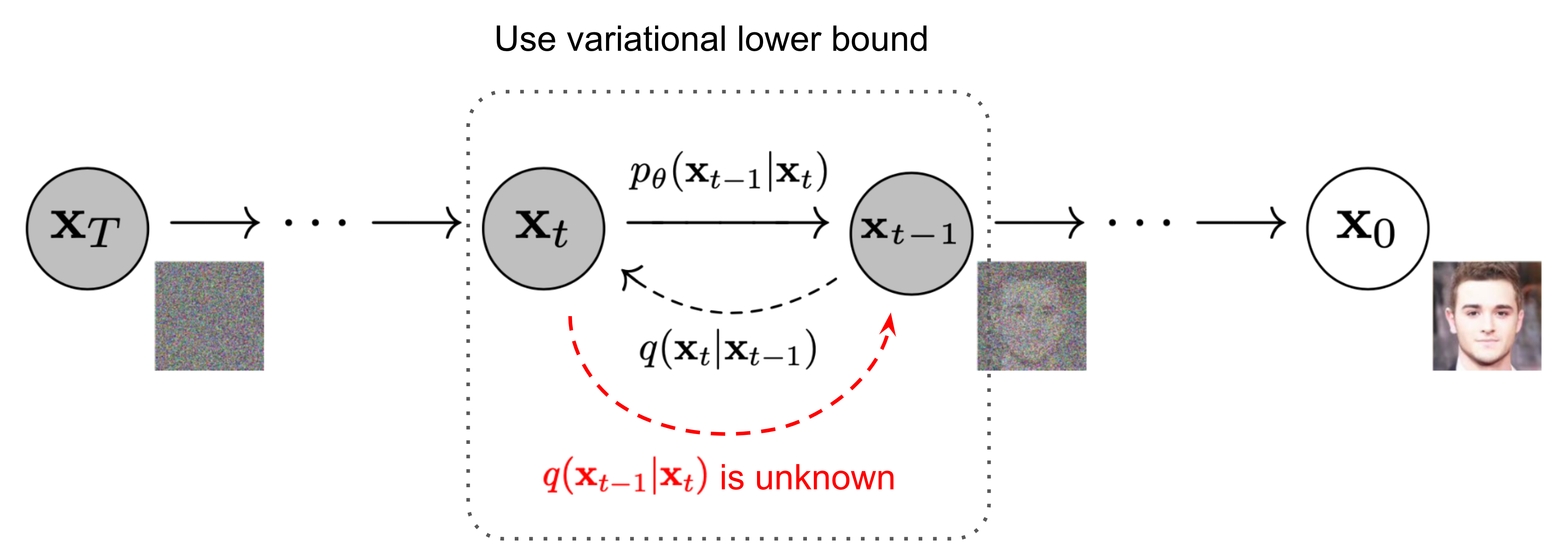
반면 Diffusion Model 에서 사용하는 확률과정의 경우 초기 시점의 데이터 분포를 복원할 수 있으면 가역적이라고 말한다. 만일 전향확률과정(forward process)의 전이 확률분포를 가지고 시간 축을 거꾸로 돌린 역확률과정(reverse process)의 전이 확률분포를 추정할 수 있다면, 역확률과정을 통해 데이터 분포에서 샘플링하는 것이 가능해지므로 가역적 변환이 된다. 이를 확률과정의 시간 역전(time reversal)이라 부르는데, 앞에서 살펴본 Diffusion Model 의 학습 원리도 Gaussian 노이즈를 주입하는 전향확률과정의 확률적인 경로를 가지고 디노이즈를 수행하는 역확률과정의 전이 확률분포를 추정하는 것이었다^[18,19]. 그러므로 Diffusion Model 은 Flow Model 처럼 생성이 결정론적이지 않고 확률적 변동성을 가지면서 샘플링 과정이 이루어진다.

확률과정의 시간 역전과 Score 기반 생성모델

앞서 설명한 Diffusion Model 의 샘플링 과정에서 주입하는 노이즈는 모드 붕괴를 막고 다양성을 보장하기 위해 필요한 장치라는 점을 기억할 것이다. 흥미로운 사실은 이러한 확률적 변동성과 함께 디노이즈를 수행하는 샘플링 과정이 노이즈를 주입하는 전향 확률과정의 시간 역전을 보장한다는 점이다 (주석: 앞서 설명했지만 확률적 변동성을 주입하지 않아도 역확률과정의 평균적인 경로를 따라 샘플링 알고리즘을 진행하면 데이터 분포에서 샘플링이 가능하다^[23].). 일반적으로 임의의 확률과정에 대해 시간 역전이 항상 가능하지는 않다. 그러나 시간 역전 이론에 의하면 Markov 확률과정의 역확률과정이 존재한다면 다시 Markov 확률과정이 되는 성질을 가지고 있다. 이 때 두 Markov 확률과정을 연결하는 필수적인 정보가 바로 Score 함수이다. Diffusion Model 에서 시간 역전이 가능한 이유도 디노이즈를 학습하는 기계학습 모델이 실은 데이터 분포의 Score 정보를 학습하도록 목적식이 유도되기 때문이다 ^[15]. 그러므로 디노이즈 기반 Diffusion Model 도 Score 기반 생성모델(SGM, Score-based Generative Model)로 통합할 수 있다 ^[23].

앞서 소개한 디노이즈 기반 DDPM^[18]은 데이터 공간과 노이즈 공간을 모두 Euclidean 공간으로 상정한다. 시간 역전 이론은 상태공간이 이산 공간이거나[24], Riemannian 다양체라도^[25] 적용하는 것이 가능하기 때문에 응용할 수 있는 데이터의 범위가 상당히 넓다. 일반적인 상태공간에서 정의된 Markov 확률과정으로 Score 기반 생성모델의 이론이 어떻게 전개되는지 궁금한 사람은 Benton et al. ^[26] 을 읽는 것을 추천한다. 본 파트에서는 Euclidean 공간에서 시간 역전 이론을 활용하여 SGM을 제시한 Song et al. ^[23]의 연구에서 출발한다.

Song et al. ^[23] 은 아래와 같이 확률미분방정식에 시간 역전 공식(time-reversal formula)^[27,28]을 적용하여 이산시간 모형인 Diffusion Model 을 연속시간 SGM으로 확장하고 데이터에 주입하는 노이즈의 크기를 시간에 따라 제어할 수 있는 학습 방법을 제안하였다. 동영상 10 과 11을 보면 Forward 와 Reverse 확률미분방정식의 경로에 따라 노이즈 주입과 생성이 어떻게 이뤄지는지 알 수 있다.

위의 Reverse SDE 식의 표류(drift) 항을 살펴보면 시간에 의존하는 Score 함수가 등장한다. 위와 같이 시간에 의존하는 계수를 가진 확률미분방정식의 시간 역전을 위해서는 Langevin 방정식처럼 데이터 분포의 Score 함수를 사용하지 않고, $X_{t}$ 의 분포에 대한 Score 함수 정보가 필요하게 된다. 그래서 Score 기반 생성모델은 각 t 시점에서 $X_{t}$ 의 Score 함수를 근사하는 Score 모델 $s_{\theta}\left(t,x\right)\approx\bigtriangledown\mathrm{log}P\left(t,x\right)$ 을 학습해서Reverse SDE 의 표류 항에 대입하여 샘플링할 때 사용하게 된다.

동영상 10: Forward 확률미분방정식에 의해 데이터에 노이즈가 주입되는 확률과정 경로 (링크)

동영상 11: Reverse 확률미분방정식에 의해 노이즈로부터 데이터가 생성되는 확률과정 경로 (링크)

디노이즈가 아닌 확률과정으로도 시간 역전이 가능할까?

DDPM^[18]이나 Song et al.^[23]에서 제안한 Forward 수식을 살펴보면 Gaussian 분포를 따르는 확률과정이 중요하게 사용된다. Diffusion Model 과 SGM 연구가 큰 주목을 받으면서 생성모델 연구자들은 다음과 같은 질문을 던지게 되었다.

“Diffusion Model 이나 SGM 학습에서 Gaussian 노이즈가 반드시 필요한가? “

위에서 이미 확률과정의 시간 역전은 Gaussian 확률과정에만 국한하지 않는다고 설명했다. 가령 경로가 연속적인 Wiener 확률과정이 아니라 불연속적인 Lévy 확률과정 기반 SGM 연구도 있다^[29]. 그런데 만약 디노이즈가 아닌 다른 방식으로 확률과정을 디자인해도 학습이 가능할까? 이에 대한 질문에서 출발한 연구들이 기계학습 분야 최고 학회 중 하나인 ICLR 에서 최근 발표되었다.

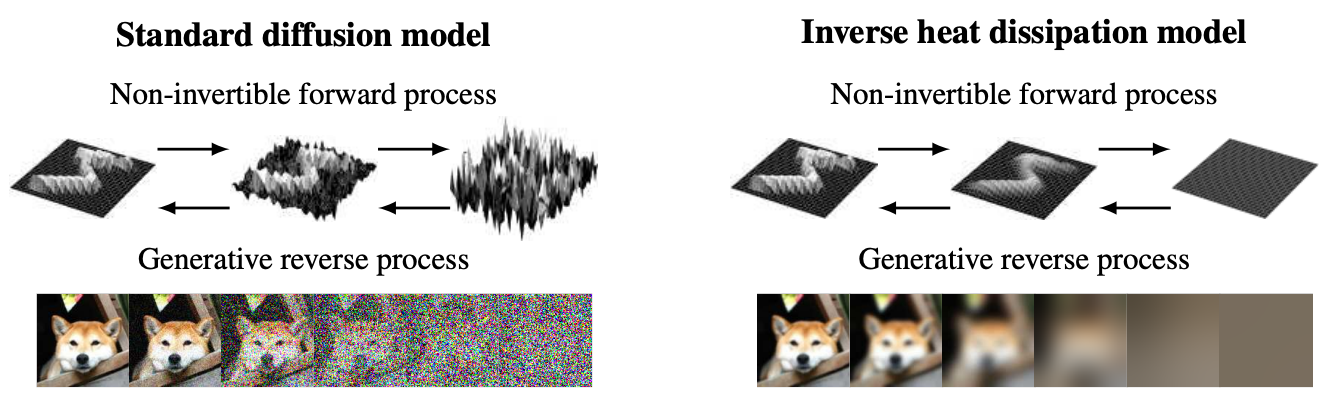
그림 12: Diffusion Model 과 IHDM[30] 비교

IHDM(Inverse Heat Dissipation Model)[30] 에서는 Gaussian 노이즈를 주입하는 확률과정 대신 열방정식(heat equation)을 이용한 생성모델 학습 방법을 제안하였다. 그림 12을 보면 Diffusion Model 과 IHDM 에서 사용하는 확률과정의 차이점을 살펴볼 수 있다. Diffusion Model에서 사용하는 노이즈 주입 방식은 픽셀간의 통계적인 상관관계 정보를 파괴하지만, 열방정식은 주변 픽셀들의 정보를 이용해서 평활(smoothing)하게 만들고 국소적으로 뭉쳐있는 정보를 전체 공간으로 확산시킨다. 그림 13을 보면 열방정식에 의해 영상 내 물체의 특징들이 점차적으로 흐릿(blur)해지는 과정을 볼 수 있다. 이렇게 데이터의 정보를 확산시켜 형성된 공간은 노이즈 공간이랑 구별하기 위해 사전분포 공간(prior space)이라 부른다.

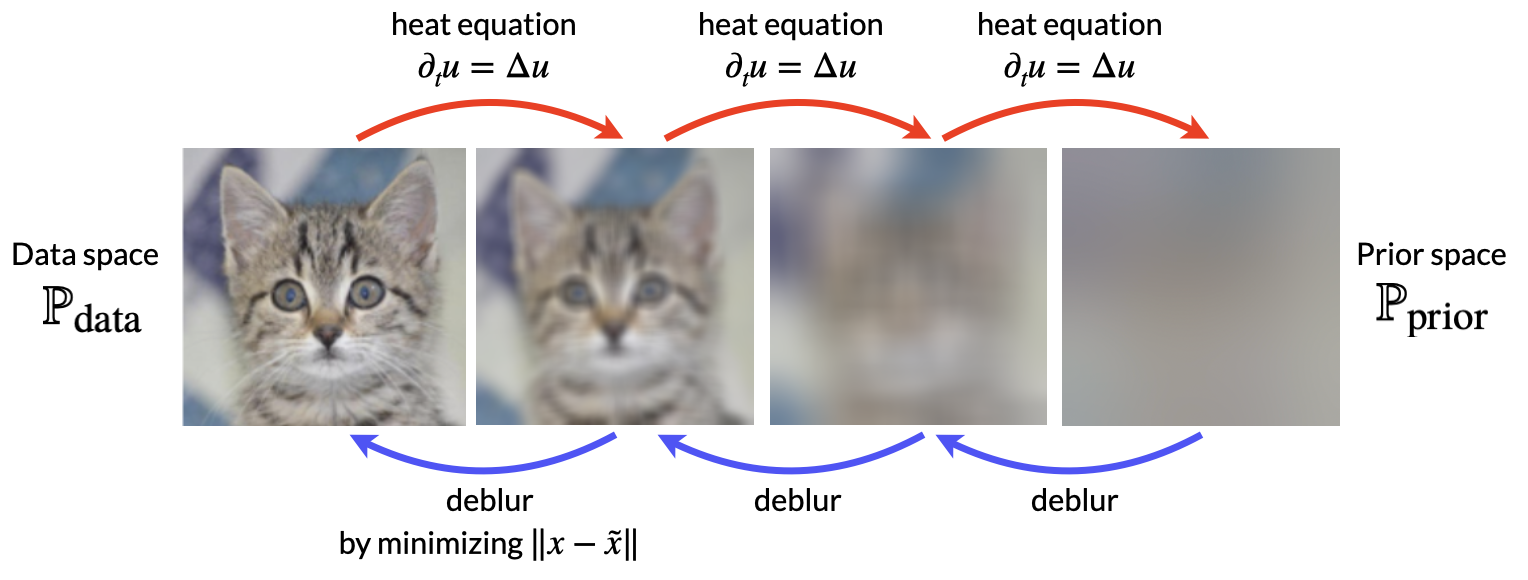
그림 13: 열방정식과 디블러를 이용해서 생성모델을 학습하는 과정

사전분포 공간에서 데이터 공간으로 매핑하는 생성모델 학습은 어떻게 디자인할 수 있을까? 자연스럽게 떠오르는 발상은 그림 13처럼 기계학습 모델이 디블러(deblur)를 학습하는 것이다. 그러나 열방정식의 역과정은 본질적으로 ill-posed 이기 때문에 디블러만 학습해서는 실제 데이터와 유사한 품질만큼 생성하는데 한계가 있다. 실제 IHDM 실험에서도 열방정식만 사용하지 않고 학습 및 샘플링 과정 모두 Gaussian 노이즈를 같이 사용하기 때문에 디노이즈와 디블러를 혼합해서 학습하게 된다. 그런데 앞서 디노이즈 기반 DSM 은 Score 함수 학습을 유도한다고 설명했다. 그렇다면IHDM처럼 디블러와 디노이즈를 같이 학습하는 생성모델은 데이터의 어떤 정보를 학습해서 샘플링을 가능하게 만들 수 있을까? 놀랍게도 데이터의 Score 정보를 역시 학습하게 된다! 디노이즈와 디블러는 전혀 다른 개념인데 어떻게 가능한걸까?

실은 Diffusion Model 에서 사용하는 데이터 공간과 IHDM 에서 정의한 데이터 공간의 성격이 달라지기 때문이다. 우선 열방정식에서 사용되는 라플라스(Laplace) 연산자 $\Delta$ 가 정의되어야 한다. 따라서 IHDM 에서는 데이터를 함수로 정의하므로 데이터 공간이 함수 공간이 된다. 그리고 함수 정의역 내부 격자점을 픽셀의 위치로 표현하여 실제 우리가 관찰하는 영상 데이터들은 유한차원 상의 기저(basis)로 사영된 것으로 인식한다. 따라서 유한차원 공간에서 정의된 확률미분방정식의 시간 역전 이론으로는 IHDM 의 학습 원리를 설명하는데 한계가 있다.

이 질문에 답하기 위해서는 확률편미분방정식(SPDE, Stochastic PDE) 이론에서 답을 찾아야 한다. SPDE 는 20세기 중반서부터 전기 및 전자공학에서 제어이나 필터링(filtering) 이론 분야에서 꾸준히 연구된 확률 방정식이다. 21세기부터는 통계물리 분야에서의 과학적 기여를 인정 받아 2014년에 Martin Hairer 가 필즈 메달을 수상하는 등 과학과 공학의 여러 분야에서 활발하게 응용되고 있다.

위 방정식은 SPDE의 한 종류인 확률열방정식(stochastic heat equation)인데, 열방정식에 화이트 노이즈(white noise)가 확산(diffusion) 항에 추가된 형태이다(주석: 엄밀히 말하면 해의 정규성(regularity)을 논하기 위해서는 사실 화이트 노이즈보다 컬러 노이즈(colored noise)를 사용하는 게 좋다. 이 부분에 대한 자세한 논의는 참고문헌 ^[31,33]을 추천한다). 확산 계수가 시간 변수 t 에만 의존하고 공간 변수인 $\mathrm{x}$ 에 의존하지 않는다면 아래와 같은 형태로 방정식의 해를 표현할 수 있다 ^[31].

여기서 $e^{\Delta t}$ 는 라플라스 연산자를 가진 지수 연산자(exponent operator)로서 초기조건이 입력으로 주어지면 열방정식의 해를 출력하게 된다. 그렇다면 위와 같은 확률열방정식의 역확률과정은 어떤 모양이 될까? 이를 유도하려면 Hilbert 공간에서 정의된 확률과정의 시간 역전 공식을 사용해야 한다 ^[33].

여기서 $\textbf{S}(t,\cdot)$ 은 데이터 공간이 정의된 함수공간 상의 연산자로 Score 연산자라 부른다 ^[33,34]. Score 연산자는 유한차원에서의 Score 함수를 Hilbert 공간으로 일반화한 개념이 된다. 그러므로 확률열방정식의 역확률과정은 디블러를 수행하는 $-\Delta$ 연산자와 디노이즈를 수행하는 Score 연산자가 결합되어 확률열방정식의 시간 역전을 보장하게 된다. IHDM 에서 제시한 생성모델의 학습방법도 이 두 연산자의 결합을 학습하는 방식으로 유도된 것이다.

IHDM 은 이산시간 모형이기 때문에 Song et al.^[23] 에서 제시한 SGM 을 일반화했다고 보기 어렵다. Hilbert 공간에서 정의된 연속시간 확률 방정식의 시간 역전 이론을 기반으로 생성모델을 디자인하려면 Score 연산자에 대한 엄밀한 접근이 필요하다. DDO(Denoising Diffusion Operator)[34] 는 불변 측도(invariant measure) 이론을 기반으로 Hilbert 공간에서 정의된 Langevin 방정식을 토대로 생성모델을 제안하였다. HDM(Hilbert Diffusion Model)^[33]은 보다 고품질의 데이터 샘플링을 위해 연속시간 모형에서 스케줄링을 활용할 수 있는 시간 역전 공식을 유도하고, SPDE를 활용한 생성모델을 제안하였다. 그림 14를 보면 HDM을 통해 샘플링한 영상들을 볼 수 있다.

그림14: SPDE 를 활용하여 학습한 Score 기반 생성모델이 생성한 영상 ^[33]

SPDE 로 학습한 Score 기반 생성모델은 여러가지 장점을 가지는데, Gaussian 노이즈나 열방정식으로 만들어낸 사전분포 외에도 blurring 이나 pixelate 를 사용한 사전분포에서도 샘플링이 가능하고, 그림 15에서 보는 것처럼 inpainting 이나 super-resolution 등 영상 복원이 추가 학습 없이 가능한 걸 보여준다. 또한 함수 공간 상의 시간 역전 이론을 기반으로 생성모델이 디자인 되었기 때문에 신경망 구조를 뉴럴 연산자(neural operator)^[35]로 바꾸면 resolution-free 생성도 가능해진
다.

그림15: SPDE 로 학습한 생성모델은 추가 학습 없이 다양한 사전분포에서 샘플링이 가능하다^[33]

맺음말

본 글에서는 생성 인공지능 연구 분야에서 주목 받고 있는 Diffusion Model 과Score 기반 생성모델의 학습 원리와 확률편미분방정식이 생성모델 연구에서 어떻게 사용될 수 있는지 살펴보았다. 본문에서는 IHDM ^[30] 에서 사용한 열방정식 중심으로 설명했지만, Cold Diffusion ^[32] 처럼 훨씬 넓은 범위의 연산자에 대해서도 Hilbert 공간 상의 시간 역전 이론에 근거하여 생성모델을 제안할 수 있다 ^[33,34]. 뿐만 아니라 매끄러운(smooth) 곡선 또는 곡면 샘플링이 필요한 모션 생성 분야에서도 사용될 수 있다.

굉장히 빠른 템포를 가진 최근 인공지능 연구 분야의 특성상 어떤 생성모델이 주류가 될지 예측하는 것은 매우 어렵다. 불과 6년 전만 하더라도 생성모델 연구자들이 주로 GAN 이나 VAE 연구에 집중했던 것처럼 Diffusion Model 을 대체하는 다른 생성모델 기법이 등장할 수도 있다. 또한 생성모델의 샘플링 품질을 높이기 위해서는 이론적 접근만으로는 한계가 있고, 여러가지 공학적 기술들을 같이 활용하는 것도 매우 중요하다 ^[4,7]. 그러나 확률론적 방법으로 기계학습 원리를 연구하는 관점에선 아직까지 풀리지 않은 궁금점들이 많이 쌓여 있는 연구 분야 중 하나라고 생각한다. 확률론이나 통계학에 관심 있는 학생들이라면 충분히 도전해볼만 분야로 적극 추천하면서 본 글을 갈무리한다.

참고문헌

확률편미분방정식과 인공지능

임성빈

고려대학교 통계학과 교수

들어가는 글 – Generative AI의 시대