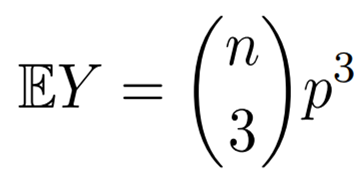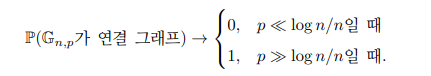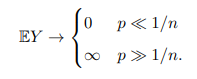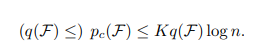무작위 이산 구조의 문지방 현상

    이 글에서는 최근에 증명된 기댓값 문지방 정리^{Expectation Threshold Theorem}에 대해 간략히 소개하고자 합니다. 확률론적 조합론 분야에서 칸–칼라이 추측^{the Kahn–Kalai Conjecture}으로 잘 알려져 있던 이 정리는 무작위 이산 구조에서 ”문지방^threshold”과 ”기댓값 문지방^{expectation threshold}” 사이에 긴밀한 관계가 있음을 보여줍니다. 본문의 첫 번째 절에서는 우선 무작위 이산 구조의 한 예인 무작위 그래프를 소개할 것입니다. 이어지는 두 번째 절에서는 무작위 이산구조의 문지방 현상을 무작위 그래프 위에서의 간단한 예로 설명할 것입니다. 마지막 절에서는 기댓값 문지방 정리를 또한 예를 통해 설명하도록 하겠습니다.
    기댓값 문지방 정리의 정확한 서술은 짧은 글에 싣기에는 다소 무리가 있어 이 글에서는 쉬운 예로 간략한 의미 정도를 전달하도록 노력하였습니다. 보다 깊이 있는 (그러나 전문적인 논문보다는 쉽게 쓰여진) 내용이 궁금하신 독자들은 [Par23](영문)을 참고하실 수 있습니다.

제 1 절   무작위 이산 구조의 예: 무작위 그래프

기댓값 문지방 정리의 주된 내용은 무작위 이산 구조의 문지방 현상이 일어나는 지점에 대한 예측입니다. 이 절에서는 우선 무작위 이산 구조의 뜻에 대해 설명하고자 합니다. 무작위 이산 구조 자체는 일반적이고 추상적인 수학적 대상이라 이 글에서는 독자의 이해를 돕기 위해 보다 구체적인 에르되시–레니 무작위 그래프^{Erdős-Rényi random graph}를 예로 들어 설명하겠습니다.
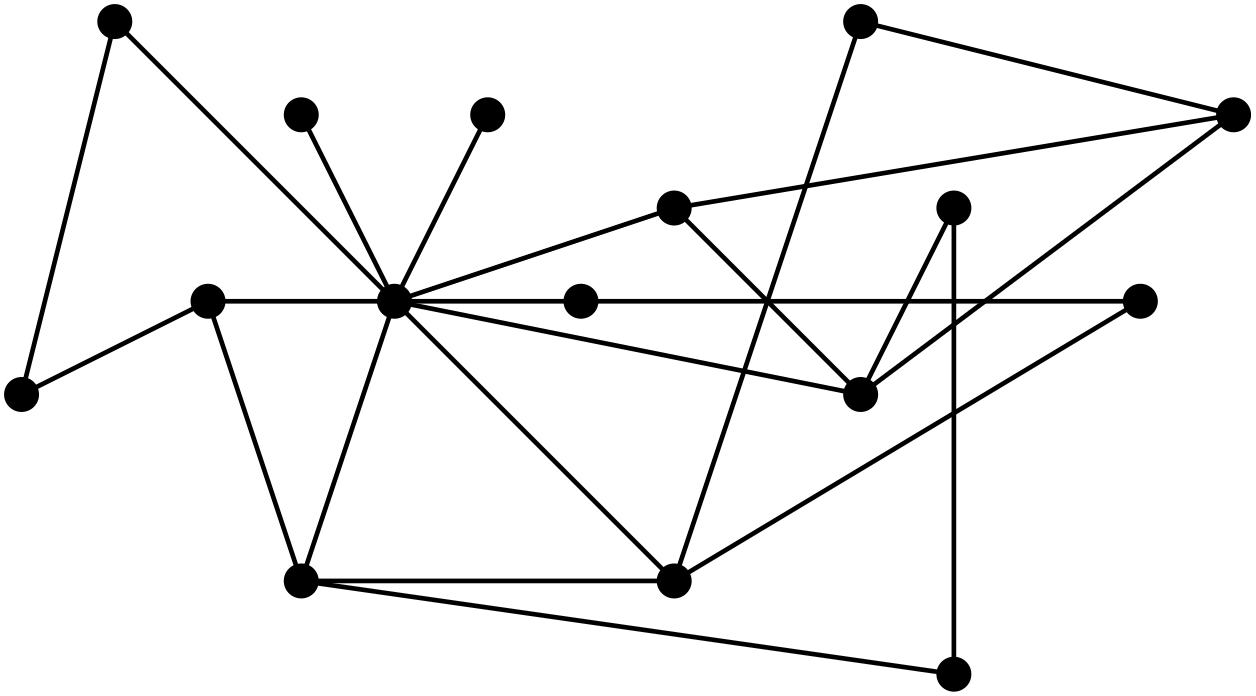
    이 글에서 그래프란 꼭짓점과 모서리로 이루어진 구조를 뜻합니다. 아래 그림에 그래프의 예가 있습니다.

    에르되시–레니 무작위 그래프 는 두 개의 변수 과  에 의해 결정되는, 그래프로 이루어진 확률공간입니다. 여기서  은 꼭짓점의 개수를 뜻하고  는 각 모서리가 존재할 확률을 뜻합니다. 평면에 1부터  까지로 이름이 붙여진  개의 점이 있다고 가정하겠습니다. (각 점에 이름이 붙어 있다는 것은 각 점을 서로 구별되는 개체로 여긴다는 뜻입니다.) 이  개의 점 중 2개의 점을 골라 연결할 때마다 모서리가 하나씩 생기므로 개의 점 위에서는 총  개의 (이름이 붙은) 잠재적인 모서리를 생각할 수 있습니다.  에서  개의 각 모서리는 확률 로 존재하며, 각 모서리의 존재 유무는 다른 모서리의 존재 유무와 독립적으로 결정됩니다. 아래에 작은 예를 들어보겠습니다.¹

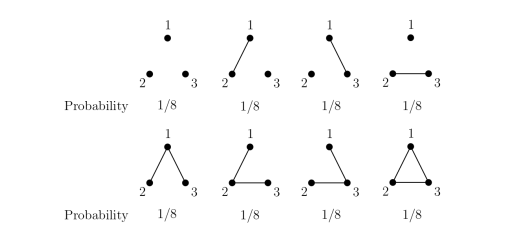
예1.1. (1)   일 때  의 꼭짓점을 3개({1,2,3})이고 잠재적인 모 서리 또한 3개({12,13,23}) 입니다. 각 모서리는 확률 1/2로 서로 독립적으로 존재하므로,  의 확률분포는 다음과 같습니다.

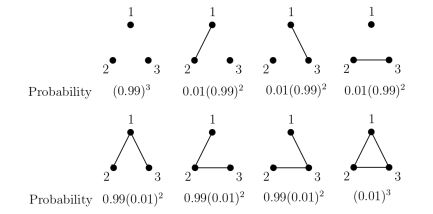
(2)  같은  에 대해서도  의 값을 다르게 할 경우  의 확률 분포는 물론 달라집니다. 예를 들어, 과 같이 의 값이 작은 경우, 밀도가 낮은 그래프가 나타날 확률이 더 높습니다. 실제로 의 확률 분포는 다음과 같습니다.

    위의 예에서 볼 수 있듯이, 무작위 그래프란 하나의 고정된 그래프가 아니라 확률 분포로 주어집니다. 이 때 표본 공간은 개의 꼭짓점을 가지는 서로 다른 개의 라벨 그래프^{labelled graph: 꼭짓점마다 서로 다른 이름이 붙여진 그래프}로 이루어지고, 각 그래프의 확률은 의 값에 따라 결정됩니다.
    무작위 그래프는 확률 변수이므로, 무작위 그래프의 연구에는 자연스럽게 확률론의 도구들이 사용됩니다. 다음은 가장 기초적인 계산의 예들입니다.

예1.2. (1) 에 모서리가 존재하지 않을 (즉, 개의 모든 꼭짓점이 고립점일) 확률은 입니다. 이렇게 모서리가 하나도 없는 그래프를 이 글에서는 빈 그래프^{empty graph}라고 부르겠습니다.

(2) 가 개의 모서리를 가질 (즉, 모든 잠재적인 모서리가 존재할) 확률은 입니다. 이렇게 모든 가능한 모서리가 존재하는 그래프를 완전 그래프^{complete graph}라고 부릅니다.

(3) 의 모서리의 개수의 기댓값을 구해봅시다. (가 확률변수이므로 의 모서리의 개수도 역시 확률변수입니다.) 를 의 모서리의 개수를 나타내는 확률변수라고 하겠습니다. 개의 꼭짓점 위에 잠재적인 모서리의 개수는 개이고, 각각의 모서리가 에서 존재할 확률은 이므로, 의 기댓값은

입니다. 예를 들어 인 경우, 는 평균적으로  개의 삼각형을 가집니다.

(4) 세 꼭짓점 위에서 정의된 완전 그래프를 삼각형이라고 부르겠습니다.  안에 존재하는 삼각형의 개수 Y 의 기댓값을 위의 예와 유사한 방법으로 구해보겠습니다. 개의 꼭짓점 위에 잠재적인 삼각형의 개수는 개이고, 각각의 삼각형이  에서 존재할 확률은 이므로,

입니다. 예를 들어 인 경우, 는 평균적으로 개의 삼각형을 가집니다.

제 2 절   무작위 그래프의 문지방 현상

앞서 는 고정된 그래프가 아닌 그래프의 공간 위에서 정의된 확률 변수임을 설명하였습니다. 무작위 그래프 이론에서 주로 관심을 가지는 주제는 과 가 주어졌을 때 의 ‘전형적인’ 구조입니다. 예를 들자면, (주어진 과에 대해) 가 99 퍼센트 이상의 확률로 만족하는 성질들에는 무엇이 있을까 하는 것입니다.

    이 문제를 거꾸로 보면, 우리가 관심있는 그래프 성질(연결성, 평면성 등)이 주어져 있을 때, 그 성질을 가 높은 확률로 만족/불만족하는 의 값을 구하는 문제로 생각할 수 있습니다. 간략하게 연결성을 예로 들어보겠습니다. 직관적으로 생각했을 때, 의 값이 아주 작으면 의 모서리의 개수는 (높은 확률로) 아주 적을 것이고, 따라서 가 연결 그래프일 확률은 0에 가까울 것입니다. 반면에 의 값이 커질 수록 의 모서리의 개수는 (높은 확률로) 많아질 것이고, 특히 가 1에 아주 가까우면 는 완전 그래프에 가까우므로 가 연결 그래프일 확률은 1에 가까울 것입니다. 그렇다면 의 연결/비연결 여부를 결정짓는 의 값을 찾을 수 있을까요? 이 문제는 무작위 그래프 이론에서 최초로 다루어진 문제들 중 하나로, Erdős와 Rényi에 의해 다음 결과가 증명되었습니다. (아래 정리에서, 두 함수 에 대해 란 이 무한대로 발산함에 따라 가 0으로 수렴함을 뜻합니다.)

정리 2.1 ( Erdős-Rényi [ER60]). 이 무한대로 발산함에 따라 다음의 정리가 성립한다.

즉, 의 연결성은 을 전후로 급격한 변화를 보입니다. 이는 무작위 그래프가 보이는 문지방 현상(threshold phenomena)의 한 예시이며, 특히 을 연결성의 문지방^threshold이라고 합니다.

    그래프의 연결성은 독자들에게 문지방 현상을 설명하기 위해 제시한 하나의 예일 뿐임을 일러둡니다. 무작위 그래프 (혹은 더 일반적으로, 무작위 이산 구조)는 훨신 더 일반적으로 모든 ”단조 성질^{monotone property}”들에 대해 문지방 현상을 보임이 Bollobás와 Thomason의 결과 [BT87] 에 의해 잘 알려져 있습니다. 여기서 단조 성질이란 모서리를 추가하는 것에 대해 불변인 성질을 말합니다. 그래프의 연결성, 비평면성, 삼각형의 존재성 등이 이에 속합니다. 보다 형식적인 언어를 이용한 문지방 함수의 정의는 다음과 같습니다.

정의 2.2. 주어진 단조 성질 에 대해 문지방 함수 란 다음을 만족하는 에 관한 함수이다.

    일반적으로 주어진 단조 성질의 문지방을 구하는 문제는 매우 매우 어렵습니다. 예를 들어, 해밀턴 회로의 존재성의 문지방을 구하는 문제는 1960년대 무작위 그래프 이론 분야의 가장 큰 미해결 난제 중 하나였으며 이는 1976년에서야 [Pos76]에 의해 해결되었습니다. 해밀턴 회로는 생성 그래프^{spanning graph}의 가장 쉬운 예중 하나이며, 일반적으로 주어진 생성 나무^{spanning tree}의 문지방을 구하는 문제는 놀랍게도 아직도 미해결로 남아있습니다.

제 3 절   기댓값 문지방 정리

     단조 성질의 한 쉬운 예로, 그래프가 삼각형을 포함하는 것을 생각해보겠습니다. Erdős와 Rényi는 무작위 그래프 안에 삼각형의 존재 유무의 문지방이 임을 증명하였습니다. 즉, 아래의 정리가 성립합니다.

정리 3.1 (Erdős-Rényi [ER60]). 이 무한대로 발산함에 따라 다음의 정리가 성립한다.

    그런데 사실 이라고 하는 값은 우리가 예 1.2 (4)에서 계산한 삼각형의 개수의 기댓값과 밀접한 관련이 있습니다. 예 1.2 (4)에서  안에 존재하는 삼각형의 개수 Y 의 기댓값이 임을 보였습니다. 따라서 을 전후로 Y 의 기댓값이 크게 변화합니다. 즉,

이 예의 경우, 이 이 {삼각형을 포함}이라는 단조 성질의 기댓값 문지방이 됩니다. 즉, 기댓값 문지방이란 쉽게 말해 기댓값의 문지방 현상이 일어나는 지점입니다.³ 

    따라서 {삼각형을 포함}이라는 성질의 경우, 어려운 증명 과정이 필요한 문지방이 사실은 쉽게 계산 가능한 기댓값 문지방과 (놀랍게도!) 일치함을 알 수 있습니다. 
    사실은, 위의 기댓값 계산이 {삼각형을 포함}의 문지방의 하계를 주는 것은 쉽게 보일 수 있습니다. 왜냐하면,  ≪ 1/n인 경우  내의 삼각형의 개수의 기댓값이 0으로 수렴하고, 이는

라는 결론을 주기 때문입니다. 즉, 문지방의 정의에 의해 {삼각형을 포함}의 문지방은 최소한 보다 는 커야 합니다. (유사한 논리로, 임의의 단조 성질에 대해 기댓값 문지방이 항상 문지방의 하계가 됨을 보일 수 있습니다.)

    정리 3.1에서 어려운 증명이 필요한 부분은 문지방의 상계, 즉,  ≫ 1/일 때

을 보이는 부분이며, 일반적으로도 많은 단조 성질들의 문지방을 구하는 데 있어서 정말 어려운 부분은 문지방의 상계를 보이는 일입니다.
    위의 삼각형의 예와 달리, 일반적으로 모든 단조 성질의 문지방과 기댓값 문지방이 항상 일치하는 것은 아닙니다. 하지만 칸–칼라이 추측이 제기되기 이전까지 알려진 모든 예들에서 문지방과 기댓값 문지방 사이의 비가 적당한 상수 곱하기  이내였습니다. 이런 관찰들에 기반하여, Kahn과 Kalai는 다음의 추측을 내놓았으며, 이는 최근에 저자와 Pham에 의해 증명되었습니다.

정리 3.2 (Park-Pham [PP02]). 절대 상수 가 존재하여, 임의의 단조 성질 에 대해 이의 문지방을 , 기댓값 문지방을 라 하면,

    정리 3.2는 정말 강력한 결과이며, 역사적으로 아주 어렵게 여겨졌던 많은 단조 성질들의 문지방을 쉬운 방법으로 구할 수 있게 해줍니다. 정리 3.2의 증명은 그 위력에 비해 놀랍도록 쉬운데, 증명의 접근방법은 Erdős와 Rado의 해바라기 추측에 관해 Alweiss-Lovett-Wu-Zhang[ALWZ]이 만들어낸 엄청난 업적과 연관이 있습니다. 재미있는 점은, 해바라기 추측이라는 문제 자체는 문지방 현상과는 조금도 관련이 없다는 점입니다. Alweiss-Lovett-Wu-Zhang의 증명법을 문지방의 상계를 구하는 데 이용할 수 있다는 놀라운 발상은 저자와 Frankston, Kahn, Narayanan에 의해 최초로 이루어졌으며, 이는 2019년 ”선형 칸–칼라이 추측”⁴의 해결[FKNP]로 이어졌습니다.

    또 한가지 흥미로운 점은, 칸–칼라이 추측에 의해 유도되는 모든 결과들은 이 추측의 약한 버전인 선형 칸–칼라이 추측에 의해 이미 유도가 가능하다는 점입니다. 2019년, 많은 확률론적 조합론 학자들의 놀라움을 불러 일으켰던 선형 칸–칼라이 추측의 증명 이후 이를 이용하여 다양한 단조 성질들의 문지방이 증명되어 왔습니다. 칸–칼라이 추측은 이론적으로는 선형 칸–칼라이 추측보다 강력하나, 칸–칼라이 추측의 강도를 이용해야만 하는 (즉, 선형 칸–칼라이 추측만으로는 유도가 불가능한) 단조 성질의 문지방은 현재까지 한 건도 보고되지 않았습니다. 실제로 선형 칸–칼라이 추측을 제기한 Talagrand는 사실 두 추측이 동치일 것이라는 추측을 남겼습니다. 이 Talagrand의 추측은 여전히 열린 문제로 남아있습니다.

참고 문헌

[ALWZ] R. Alweiss, S. Lovett, K. Wu, and J. Zhang. Improved bounds for the sunflower lemma.Ann. of Math. (2) 194 (2021), no. 3, 795–815.
[BT87] B. Bollob´as and A. Thomason. Threshold functions. Combinatorica 7 (1987), 35-38.
[ER60] P. Erd˝os and A. R´enyi. On the evolution of random graphs. Publ Math Inst HungarAcad Sci 5 (1960), 17-61.
[FKNP] K. Frankston, J. Kahn, B. Narayanan, and J. Park. Thresholds versus fractional expectation-thresholds. Ann. of Math. (2) 194 (2021), no. 2, 475-495.
[Par23] J. Park. Threshold phenomena for random discrete structures. Notices of the American Mathematical Society, to appear.
[PP02] J. Park and H. T. Pham. A proof of the Kahn–Kalai Conjecture. Journal of the American Mathematical Society, to appear.
[Pos76] L. P´osa. Hamiltonian circuits in random graphs. Discrete Math, 14 (1976), 359-364.
[Tal10] M. Talagrand, Are many small sets explicitly small?. STOC’10 – Proceedings of the 2010 ACM International Symposium on Theory of Computing, 13-35, ACM, New York,2010.