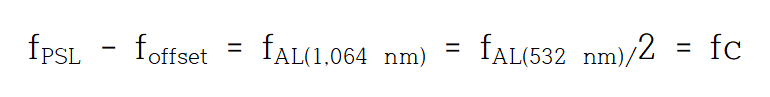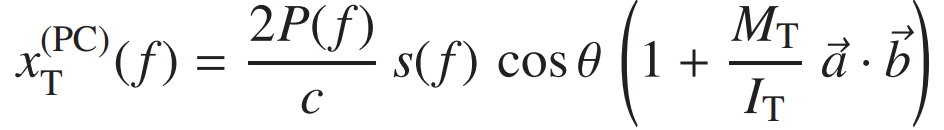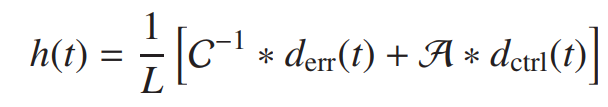라이고 중력파 검출 신호의 이해와 중력파 신호 교정

 본 아티클에서는 지난달에 게재된 아티클(레이저 간섭계 중력파 관측소(라이고, LIGO)의 레이저 간섭계)에 이어서, 고급 레이저 간섭계 중력파 관측소(a-LIGO)의 레이저 간섭 시스템을 이용한 중력파 검출과 간섭계의 정확도를 보증할 중력파 신호의 교정에 대해서 살펴보도록 하겠습니다.

2015년 최초의 중력파 “GW20150914”를 관측한 이후 지난 8년 동안 지상 기반 레이저 간섭계인 LIGO와 Virgo가 쌍성 블랙홀과 중성자별의 합병에 대한 많은 수의 중력파를 관측함으로서 우주에 대한 완전히 새로운 창을 열었습니다.
아토헤르츠(10^-18 Hz)에서 킬로헤르츠(10³ Hz) 주파수까지 확장되는 중력파 스펙트럼은 물리학과 천문학의 많은 근본적인 질문을 탐구할 수 있는 비옥한 토대를 제공합니다.

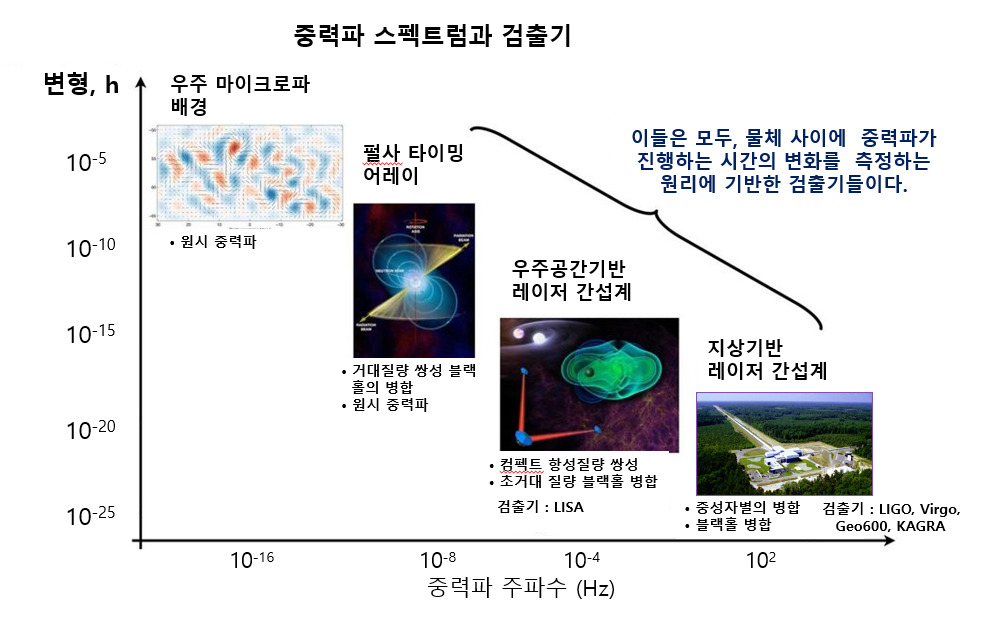
그림 1은 중력파의 파원에 따른 중력파 주파수 및 변형의 크기와 이를 검출하기 위한 중력파 검출기들을 나타낸 그래프입니다.^[1]

우주 마이크로파의 배경복사로 극히 미약한 극저주파수의 원시 중력파를 탐구할 수 있으며, 펄사 타이밍 어레이는 현재 나노 헤르츠에서 마이크로 헤르츠 주파수 대역을 조사하여 과거 초 거대 질량 블랙홀 합병의 중력파 잔해를 감지합니다. 우주 기반 레이저 간섭계 우주 안테나^{LISA, Laser Interferometer Space Antenna}는 마이크로헤르츠(10^-6 Hz)에서 최대 수백 밀리헤르츠(10^-3 Hz)까지의 중력파 소스를 표적으로 삼고 초기 우주에서 별 형성 시대의 정점까지 블랙홀의 진화를 추적합니다. 이보다 주파수는 더 높으나 변형 더 낮은 중성자별의 병합이나 쌍성 블랙홀의 병합과정에서 생성된 중력파는 지상 기반 레이저 간섭계(LIGO, Virgo, GEO600, KAGRA)들을 사용하여 관측합니다.

후자의 3종류의 검출기는 모두 두 물체 사이의 중력파의 진행 시간 변화를 측정하는 원리에 기반한 검출기입니다.

그림 1. 중력파 스펙트럼과 검출기 우주 마이크로파의 배경복사로 극히 미약한 극저주파수의 원시 중력파를 탐구할 수 있으며, 펄사의 타이밍 어레이 안테나들로 부터 거대 질량의 쌍성 블랙홀이 병합할 때 생성되는 중력파나 우주의 생성 초기 원시 중력파를 탐구하며, 컴팩트한 항성질량 쌍성이나 초거대 질량 블랙홀의 병합과정에서 발생하는 중력파는 이보다 더 주파수가 높고 변형이 크므로, LISA로 검출하고 탐구합니다. 이보다 주파수는 더 높으나 변형감도가 더 낮은 중성자별의 병합이나 쌍성 블랙홀의 병합과정에서 생성된 중력파는 지상기반 레이저 간섭계(LIGO, Virgo, GEO600, KAGRA)들을 사용하여 관측합니다.

지상 기반 레이저 간섭계, 고급 라이고의 중력파 변형 측정 민감도와 잡음

지상 기반 레이저 간섭계로 중력파를 관측하기 위해서는 중력파 변형 10^-21을 신호대잡음(S/N)비 10:1 이내로 측정하려면 잡음을 중력파 검출 대역폭에서 10^-22 이내로 검출기의 잠음을 제어하여야 합니다. 이와 같은 저 잡음의 중력파 변형의 측정 감도를 확보하고 잡음을 제어하기 위한 여러 가지의 노력에 기울여졌습니다. 다음에는 이들 잡음에 대해 기술합니다.

레이저 간섭식 검출기의 산탄(shot) 잡음
레이저 간섭식 검출기는 레이저가 무작위로 방출되는 광자를 이용하기 때문에 본질적으로 발생하는 산탄 잡음에 의해 고주파수 영역에서 측정 감도는 제한을 받습니다. 이를 무수히 떨어지는 물방울에 의한 강우량에 비유됩니다, 광자는 떨어지는 빗방울과 같이 임의의 시간에 떨어지며 평균값 주위의 변동을 일으킵니다. 이로 인해 광검출기의 출력에서 출력 잡음이 발생합니다.

또한, 충분히 높은 레이저 출력의 경우, 레이저 광자에 의해 테스트 질량(거울)으로 전달되는 임의의 운동량이 거울을 흔들어 저주파에서 신호에 잡음을 더합니다. 잡음의 크기는 광자수 N의 (-1/2) 제곱승(: ~/√N)에 비례하므로 레이저의 출력이 높아질수록 shot 잡음은 줄어듭니다. 그러므로 고급 라이고에서는 테스트 질량들로 구성된 파브리-페로 간섭계 내부 출력을 750 kW 까지 올려놓았습니다.

또, 레이저 빔이 측정하고자 하는 테스터 질량(거울)면을 때리거나 테스터 질량이 매달려 있는 서스펜션에 생기는 열 잡음(예: 브라운 운동)는 중력파 변형 측정 감도의 또 다른 한계입니다. 이러한 “고정”(일정한) 소음원 외에도 모든 지상기반 검출기는 지진 소음 및 기타 형태의 환경 진동 및 기타 “비-고정” 소음원에 의해 저주파 영역에서 제한을 받습니다. 기계적 잡음, 번개 또는 기타 큰 전기장애 등의 삐걱거리는 소리 또한 중력파 신호를 덮는 마스킹 잡음을 생성하거나 중력파 검출 이벤트를 모방한 신호를 만들 수도 있습니다. 이 모든 것을 고려하고 분석하고 제거하고 검출하여야 진정한 중력파 이벤트로 간주될 수 있습니다.

그러므로, 레이저 간섭계의 잡음 스펙트럼의 밑바닥은 기본 잡음 소스, 양자 잡음 및 열잡음(예:브라운 운동)에 의해 결정됩니다. 열잡음은 간섭계에 사용한 재료 특성 및 빔 크기와 같은 간섭계의 고정 매개변수에 의해 결정됩니다. 반면에 양자 잡음은 쉽게 변경할 수 있는 입력 레이저 출력과 보다는 덜 쉽게 변경할 수 있는 중력검출 신호 재활용 거울(SRM)에로의 전송에 따라 달라집니다.

레이저 주파수 또는 진폭 잡음, 광검출기 다크 잡음, 액추에이터 잡음 등과 같은 기타 잡음 소스는 제어 가능한 ‘기술’ 잡음으로 분류됩니다. 기술적 잡음은 각 소스의 등가 변형 잡음이 감지 대역(10 Hz ~ 7 kHz) 전체에서 목표 변형 민감도의 10%를 넘지 않도록 설계에 의해 제어됩니다. 이러한 잡음 소스는 통계적으로 독립적이므로 전체에 루트 제곱 합으로 추가됩니다. 따라서, 개별 10% 잡음 소스는 잡음의 밑바닥을 0.5%만 증가시킵니다.

양자 잡음: 양자잡음은 검출된 광자의 산탄 잡음의 통계적 변동과 광자 수 변동으로 인한 복사압의 영향을 포함합니다.

테스트 질량의 열잡음: 다양한 테스트 질량 열잡음 중에 코팅한 재료의 브라운 운동에 의한 열잡음이 지배적입니다.

지진잡음은 지상에서 조수, 파도 폭풍에 이해 발생되는 지진 표면파를 포함하는 진동잡음이며 관측되는 0.1 Hz 미만에서 지배적인 잡음이며 100 Hz이상의 높은 주파수 영역에서는 양자잡음이 지배적입니다.

서스펜션 열잡음: 테스트 질량의 서스펜션의 열잡음은 주로 최종 서스펜션 단계에서 사용되는 테스트 질량을 매단 4줄의 용융 실리카 섬유의 열운동에 인한 것입니다.

중력 기울기 잡음: 지진파는 테스트 질량에 가까운 지구에서 밀도 섭동을 생성하고, 이는 차례로 테스트 질량에 변동하는 중력을 생성합니다. 이 지진 중력 기울기 잡음은 테스트 질량에 대한 서스펜션 시스템의 큰 기계적 격리로 인해 이 소음은 11 Hz이상에서는 무시할 수 있습니다.

잔류(과도) 가스 잡음: 4 km 길이의 빔 튜브에 있는 잔류 가스는 빔 경로에 있는 가스 입자의 컬럼 밀도에 통계적 변동을 일으켜 유효 온도의 변동을 생성합니다. 경로를 따른 굴절률 변동 즉, 광 경로 광학 길이 변동 잡음입니다.

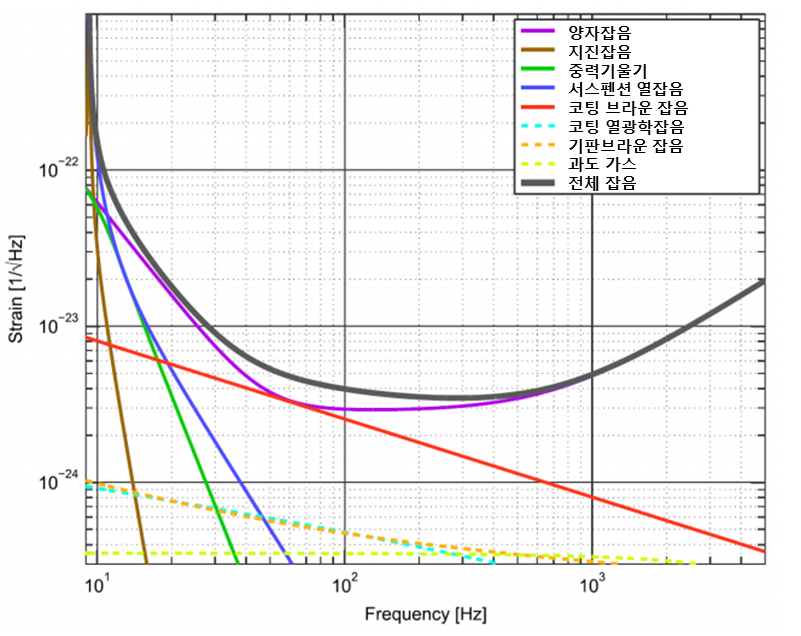
그림 2 에는 이들 잡음이 종합된 고급 라이고의 고출력, 광대역 작동 모드에서의 변형 측정의 한계를 나타내는 민감도를 나타내었습니다. 30 Hz에서 2.5 kHz 사이에서 10^-23 의 잡음 감도를 갖습니다. 이 대역에서는 중력파 검출이 용이하게 됩니다.

그림 2. 고급 라이고의 고출력, 광대역 작동 모드에서의 주요 잡음^[2]

전역 감지 및 제어

파브리-페로 마이켈슨 레이저 간섭계에서는 광속분할기를 중심으로 하여 핵심 광학계 사이에는 아주 복잡한 다중 광 결합된 공진기들로 형성되기 때문에 공진기들을 제어하는 신호도 복잡하게 서로 얼켜져 있으며.^{[3] 고급 라이고에서 제어해야 전체 파라미터 수가 모두 300여 개가 됩니다. (1개 광학 공진기의 예를 들면, 공진기 길이 연관 자유도는 5개이며 각도 및 정렬에 관련된 자유도는 10개입니다. 1 개의 공진기에서 총 15개의 자유도가 제어되어야 합니다.)} 간섭계의 각종 광검출기를 통해 생성된 오차 신호들을 사용한 능동 피드백을 사용하여 간섭계를 적절한 동작 상태로 제어 유지해야 합니다.

 여기에는 4개의 간섭계 공진기를 공진 상태로 유지하고(2개의 암 공진기, 출력 및 신호 재활용 공진기) 마이켈슨 간섭계을 다크 프린지(또는 거기에서 더해서 약간의 오프셋을 제어하여야 한다.)에 유지해야 합니다. 또한 전체 간섭계를 적절한 각도 정렬로 유지하려면 전역 제어가 필요합니다. 길이 및 정렬 자유도에 대한 광학 감지는 간섭계의 5개 출력 포트에 위치한 광검출기에서 얻을 수 있습니다.

• 반사 포트^REFL: 출력 재활용 거울에서 반사된 빛. 빔의 출력 ~10 %가 감지됩니다.
• POP(출력 재활용 공진기 안의 Pick-off Port): PR2에서 전송되는 광속분할기에서 오는 것; 일반적으로 빔의 ~10 % 가 감지됩니다.
• 반대칭 포트^AS: 신호 재활용 거울에서 나가는 빔. 빔의 99%는 DC-판독 광검출기로 향하고 1 %는 정렬 및 보조 감지기로 향합니다.
• ETM 투과(TRX 및 TRY): 두 개의 최종 테스트 질량을 통과한 투과 빔으로 빔의 몇 퍼센트가 감지됩니다.

공진기 길이 감지 및 제어

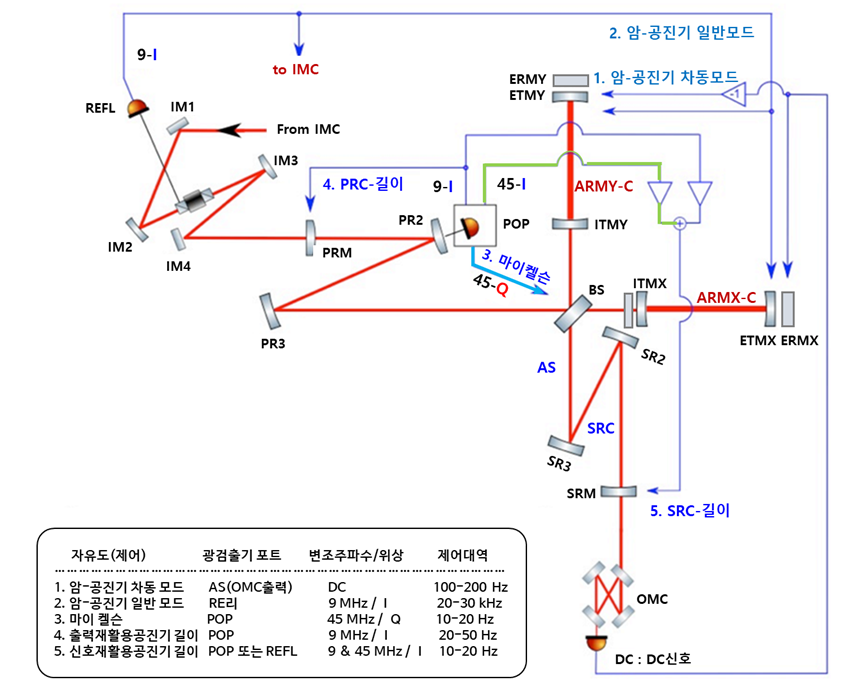
그림 3에는 각 공진기의 길이 감지 및 제어 장치의 개략도를 나타낸 그림입니다. 네모 박스 안에는 제어할 5가지 공진기 길이 자유도와 제어를 위한 광검출기 포트, PDH-제어 회로를 위한 기준신호의 위상 및 제어 대역폭을 나타내었으며, 광학계의 그림에는 전체 제어 루프를 나타내었습니다. 이후 개선되는 암 공진기 차동 모드와 암 공진기 제어, 사전안정화레이저의 다크 간섭무늬 옵셋 제어는 2대의 보조레이저를 이용하여 수행합니다. (그림 4 참조)

제어 길이 감지 방식은 초기 라이고^[3]에서 사용된 방식과 유사하지만, 고급 라이고에서는 새로운 신호 재활용 공동의 길이를 감지하도록 확장되었습니다. 암-공진기 길이는 공통 및 차동 모드를 기준으로 처리됩니다. 전자는 레이저 주파수에 공진하는 평균 암-길이이고 후자는 중력파 신호 검출모드인 암 길이 차동 모드^DARM 입니다.

레이저 주파수 변조를 위해 두 세트의 RF변조 측파대가 레이저에 적용됩니다. 하나는 9 MHz 이고 다른 하나는 45 MHz 변조 주파수입니다. 두 쌍의 RF측파대는 출력 재활용 공진기에서 공진하지만 암-공진기에서는 공진하지 않습니다. Michelson은 일반적인 Schnupp 비대칭^{그림3의 광속분할기(BS)에서 X-축 입력테스터질량(ITMX)까지 거리와 Y-축 입력테스터질량(ITMY)까지 거리가 같지 않은 비대칭성} 포함하므로 반송파가 다크 프린지에 있을 때에도 RF측파대 출력이 AS포트로 전송됩니다.

RF-판독 방식을 이용하던 초기 라이고에 비해, DC-판독식을 이용하는 고급 라이고에서는 광속분할기 BS 아래 방향(레이저 간섭 출력 포트)의 비대칭 포트에서 나온 신호를 신호 재활용 공진기를 통해 저 잡음으로 증폭시키고 다시 기본 모드인 TEM₀₀모드 이외의 고차 횡모드를 다시 한번 더 출력 모드 클리너(OMC)에서 필터링 한 후 다크 프린지에서 12 pm정도 옵셋된 위치에서 수십 mW 정도의 출력 신호를 얻고, 이 신호를 공진기 길이의 차동 모드 제어 신호와 이 신호에 실리게 될 중력파 신호를 얻어 중력파 검출에 활용합니다.

이 제어 신호를 X–암 공진기는 정궤환 신호로, Y-암 공진기에는 부궤환 신호로 활용^{최종 반작용 질량-X, ERMX의 정진기 액츄에이터에 가하고 최종 반작용 질량-Y, ERMY의 액츄에이터에는 부궤환 제어신호를 가하여, (Lx-Ly) 길이를 제어하게 됩니다.}하므로서 두 파브리-페로 공진기의 차동모드 즉, Lx-Ly = L- 값을 안정화하게 되고, 중력파가 들어오면 제어 회로 내부에서 이에 비례하는 오차신호를 얻어 공진기 길이 L 나눈 변형 h(t)을 측정하여 중력파를 검출하게 되는 것 입니다.

이 과정을 중력파 신호의 교정 섹션에서 다시 제어 회로를 이용하여 설명하도록 하겠습니다.

그림 3. 고급 라이고의 공진기 길이 센싱 및 제어 도식도

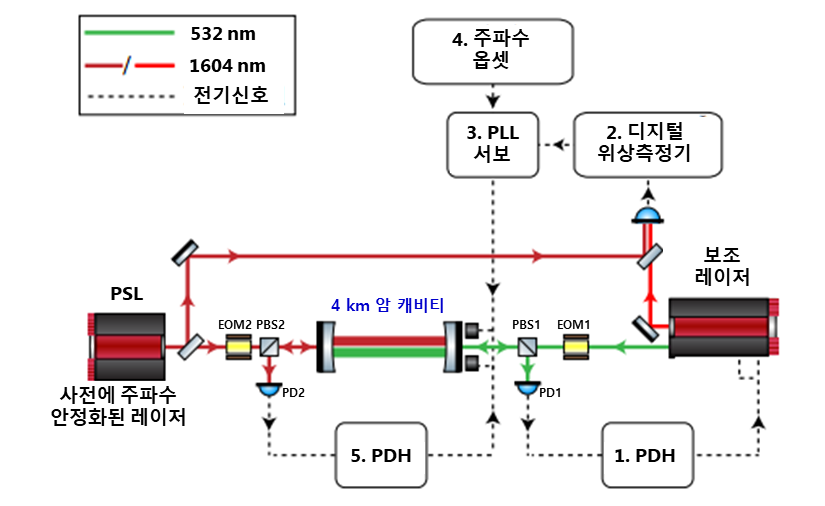
그림 4. 2파장 Nd:YAG 레이저를 이용한 암 공진기 안정화

다음은 보조레이저^{Auxiliary Laser, AL}를 이용하여 4 km 공진기의 안정화와 사전안정화레이저의 다크 프린지(간섭 신호)의 인접 점에서 옵셋 안정화와 중력파 검출 신호에 대해서 기술합니다.^{[4, 5]}

그림 4에는 2파장을 갖는 Nd:YAG 레이저(1,064 nm & 532 nm, )를 이용한 사전안정화레이저 주파수 의 옵셋에 수직하게 설치된 두개의 파브리-페로 공진기(L = 4 km)의 각각의 공진주파수 fc와 옵셋 안정화하는 원리를 나타내었습니다.

그림의 왼쪽의, 전체 레이저 간섭계에 사용하는 레이저로서의 사전 안정화 레이저 PSL에서 나온 1,064 nm 레이저 빔을 이용하여 ‘5. PDH’-안정화법으로 4 km의 기본 공진기의 길이를 점선과 같은 루프를 이용하여 사전안정화레이저(PSL) 주파수에 공진하도록 1차적으로 액츄에이터에 제어신호를 가하여 공진기 길이를 제어를 합니다. (실제로는 두 공진기 길이(Lx 및 Ly)를 각각의 2 대의 보조레이저를 이용하여 제어하고 암 공진기 차동 모드도 그림 3에 보이는 방법과 같은 방법으로 제어합니다)

다음으로, 안정화된 4 km 파브리-페로 공진기(공진주파수, fc)에 보조레이저의 주파수()를 ‘1. PDH’-안정화법으로 오른쪽에 있는 점선과 같은 루프를 이용하여 안정화합니다. 4 km 공진기는 보조레이저 주파수 와 광대역 제어 대역폭(≥ 10 kHz) 안에서 제어되어 더 단단하게 공진하게 됩니다.

그 다음으로는 사전 안정화 레이저(PSL, 파장: 1,064 nm) 주파수 과 주파수의 1/2인 주파수를 갖는  레이저 사이의 비트(beat, 맥놀이) 주파수의 위상을 ‘2. 디지털 위상측정기’를 이용하여 측정하고 그 위상과 ‘4. 주파수 옵셋()’에서 만들어진 기준 주파수 신호 사이의 위상을 비교하여, 위상 동기 서보 루프 ‘ 3. PLL 서보’를 작동시키고, 기본 암 공진기를 길이를 사전안정화레이저 주파수 의 옵셋()에 안정화 시킵니다.

위상 동기 서보 루프(PLL 서보)의 오프셋 주파수()를 조정함으로써 사전안정화레이저 주파수 의 공진으로부터의 디튜닝을 능동적으로 제어할 수 있습니다.

긴 베이스라인 레이저 간섭계에서는 이 기능을 사용하여 암 공진기을 공진으로부터 고정된 오프셋으로 유지하여 외부 교란의 방해 없이 단단히 고정되도록 할 수 있습니다.

이제 공진으로 인한 암의 오프셋을 체계적인 방식으로 줄여 간섭계 중력파 획득 신호가 활성화될 수 있는 영역으로 공진기의 길이를 맞출 수 가 있습니다.

중력파 검출실험에서 12 pm 정도의 옵셋을 주도록 ‘4. 주파수 옵셋(=())’값을 조정한 것으로 알려져 있습니다.이때, 12 pm 에 상당하는 옵셋 주파수는 foffset = 0.845 Hz가 됩니다. (,  f는 1,064 nm 파장의 PSL 레이저 주파수)이 경우에 공진기의 공진주파수 fc, 사전안정화레이저의 주파수 , 보조레이저의 주파수 , 주파수 옵셋 사이의 관계식은 다음과 같습니다. (옵셋 길이가 12 pm인 경우에 대해 이들 관계를 그림. 5에 그려 넣었습니다.)

중력파 검출 신호의 이해

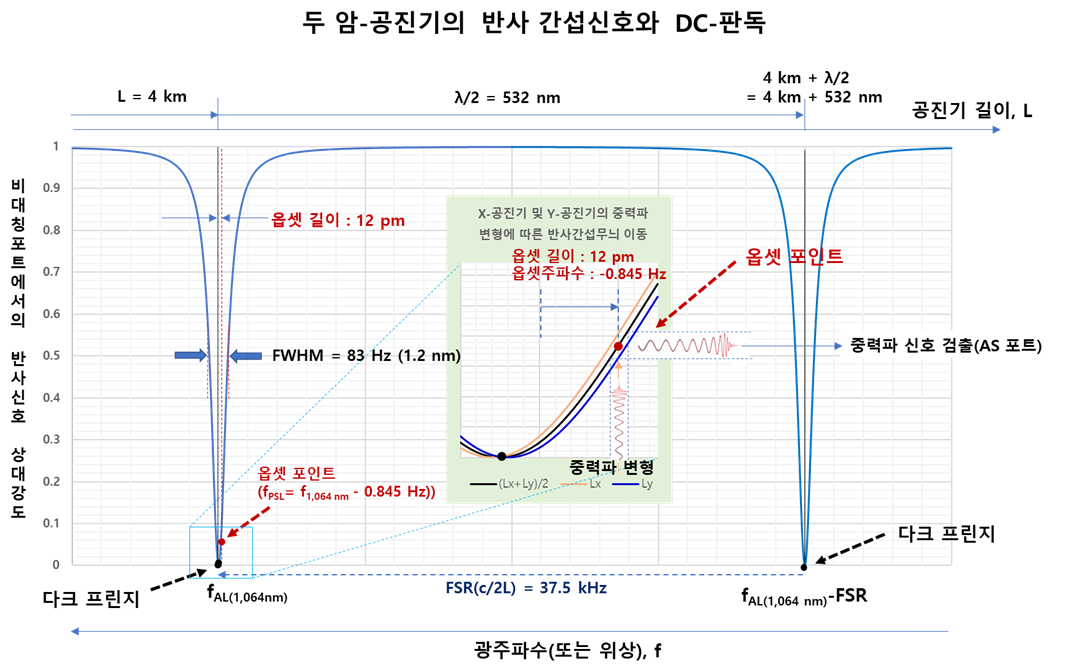
다음은 이와 같은 관계를 이용하여 레이저 간섭계의 비대칭 포트에서의 두 개의 기본 암-공진기에서 반사된 간섭 신호와 DC-판독과 중력파 신호검출에 대해 그림 5를 이용하여 설명합니다.

그림 5. 주공진기에서 반사된 간섭신호와 DC-판독 및 중력파 검출 원리

그림 5에서 두 파브리-페로 공진기의 반사 간섭무늬의 상대 강도를 나타낸 그림이며, 그림에서 X-축은 주 공진기의 길이 또는 광주파수를 나타내며, Y-축은 레이저 간섭계의 비대칭 AS 포트에서의 반사 간섭신호의 상대 강도를 나타냅니다.

암-공진기의 길이 L은 4 km이므로, 자유스펙트럼너비 ^{FSRFree Spectral Range, c/2L} 는 37.5 kHz 이고, 공진기의 간섭무늬 예리도^Finesse가 450인 것으로 부터 스펙트럼의 FWHM^{Full Width Half Maximum} 이 83 Hz임을 알 수가 있습니다. 앞에서 설명한 바와 같이 간섭무늬의 신호가 가장 낮은 다크 프린지 점^{주공진기 길이 4 km가 보조레이저 파장이 공진되는 점이며, 이 점들은 주기적으로 나타나는데 길이 간격으로는 레이저의 반파장(532 nm) 주기로, 주파수로는 FSR(37.5 kHz) 간격으로 주기적으로 나타납니다.}에서 12 pm 떨어진 곳(옵셋 포인트)에서 보조레이저 주파수가 일치하도록 하여 중력파 신호를 검출하게 됩니다.

그림 5의 가운데 아래부분과 같이, 중력파에 변형에 의해 공진기 길이  와  가 서로 반대 방향으로 진동하면(가운데 그림의 아래 진동), 변하지 않는 사전안정화레이저^PSL 주파수 이 일정하게 고정되어 있으므로, PSL 입장에서 보면 옵셋 포인트에서 두 간섭무늬 크기와 위상 차이가 생기고 이 차이는 그림의 오른쪽 모양으로 진동하는 중력파 변형의 간섭 신호를 비대칭 포트에서 얻을 수가 있습니다. 이 신호는 신호 재활용 공진기 SRC를 통해 증폭되고 출력 모드 클리너 OMC 를 거쳐 광검출기에서 검출되어(그림 3 참고), 그 신호의 일부는 그림 13.의 암-공진기 차동 모드 제어 서보의 암-공진기 길이 변화 신호 포트로 입력됩니다. 중력파 변형에 비례하는 이 두 간섭 신호의 차이는 암-공진기 차동 모드로서, 단일 레이저를 이용한 경우, 그림 3의 ‘1. 암-공진기 차동 모드는 X-축 공진기에 포지티브(+1) 증폭기와 Y-축 공진기의 네가티브(-1) 증폭에 의해 생성됩니다.

같은 메카니즘으로, 2대의 보조 레이저를 이용한 개선된 구조에서는 그림 4에서와 같이, ’3. 서보 PLL’ 출력단(2대의 보조 레이저-1(X-축) 및 보조 레이저-2(Y-축))의 2개의 제어신호로 부터 차동 위상 신호를 만들고, 이를 이용하여 중력파 검출 신호를 얻을 수가 있습니다. 중력파 변형에 의해 X 및 Y의 각각 공진기 길이의 변형이 생기면 보조 레이저의 위상이 각각 변동되어 공진의 공진주파수를 트래킹하기 때문에 이 차동 위상 신호는 두 공진기의 길이 변형의 차이에 비례하므로 중력파 검출 신호로 이용될 수가 있습니다.

자세히, 간섭무늬의 진폭 항과 위상 항을 분리하여 중력파 신호검출을 설명합니다.

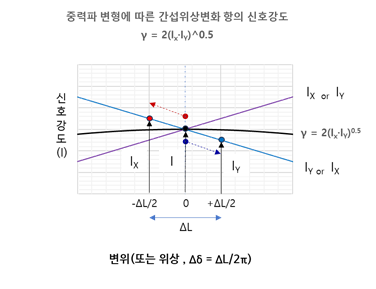
중력파 변형에 의한 X-축 과 Y-축 암-공진기의 의한 반사에 의한 마이켈슨 간섭의 위상변화의 항 γ 는 두 신호의 신호강도(I_X, I_Y)의 기하평균 _Y = 2(I_x·I_Y)^0.5 이며,  (X축 암-공진기에서 반사한 전기장 E_X 에 의한 광강도 I_X ∝ E_X² 와 Y축 암-공진기에서 반사한 전기장 E_Y 에 의한 광강도  I_X ∝ E_Y² 이고,) 비대칭 포트에서의 마이켈슨 간섭무늬 신호 강도 I (I = I_x + I_Y + 2(I_x·I_Y)^0.5cos δ = I₀ + γ·cos δ) (본 과학의 지평 아티클, ‘미터의 정의와 레이저’의 섹션 3-1-2의 그림 6의 광 간섭계의 I 값 참고)의 코사인 항의 진폭으로 주어집니다.

그림 6. 중력파 변형에 의한 간섭위상변화 항의 신호강도, γ

중력파 변형에 의해 LX 공진기 길이가 줄어들면 공진특성 곡선은 왼쪽으로 이동하여 붉은 색 곡선처럼 되고(그림5 가운데 그림), 이때 변하지 않고 있는 PSL 레이저 광이 느끼는 공진기의 전기장의 크기는 그림 6의 붉은 색의 직선과 같이 증가한다. 반대로 중력파 변형에 의해 LY 공진기 길이는 반대로 늘어나서 공진특성 곡선은 오른쪽으로 이동하여 푸른색 곡선처럼 되고 이때 변하지 않고 있는 PSL 레이저 광이 느끼는 전기장의 크기는 그림 6의 푸른색과 같이 감소한다. 이 두 전기장의 광강도 크기의 기하평균이 그림 6의 가운데 검은 색의 곡선과 같이 되고 가운데에서는 크기 변화 없이 값이 일정하다. 중력파 진폭이 극히 작기 때문에 중력파의 시공간 변형에 의해 두 공진기에서 반사 간섭된 광 간섭에서 광출력 변화는 일어나지 않는다.(Δγ = 0) 그림 5의 중력파 변형에 의한 위상 차이(Δδ = δX-δY) 만 감지되어 그림 5와 같이 비대칭 포트에서 중력파에 의한 시공간 변형에 비례하는 위상변화만 감지되어 광검출신호가 검출됩니다.

중력파 변형에 의해 그림 5의 X-축 및 Y-축 암-공진기 반사광 강도 I_X 및 I_Y 는 그림 6의 푸른 색과 붉은 색의 점과 같이 변화하게 되고, 그 기하평균 γ = 2(I_x·I_Y)^0.5 가 되므로 중력파 미소 변형에 의해서는 γ 값은 변화가 없고, 위상변화(Δδ = δ_Y – δ_X = ((ΔL/2)/2π-(ΔL/2)/2π = ΔL/2π)는 중력파 변형에 따라 선형적으로 변하게 됩니다.

두 암-공진기에 의한 비대칭 포트에서의 마이켈슨 간섭 신호 변화항 γ·cos δ 에서 γ 에 의한 광출력 진폭 변화는 일어나지 않습니다. (Δγ = 0), 다만, 그림 6에서와 같이 중력파 변형(ΔL)에 의한 위상 변화(Δδ) 에 의한 광출력 변화만 감지됩니다. 즉, 그림 5와 같이 비대칭 포트에서는 중력파에 의한 시공간 변형에 비례하는 위상변화에 의한 광출력 변화가 감지되어 광검출 신호가 검출됩니다.

이중 재활용 공진기와 Michelson 간섭계의 길이 안정화

한편, 그림 4. 2파장의 Nd:YAG 보조 레이저를 이용한 암-공진기 옵셋 안정화에 이어 잠금 획득의 2단계는 이중 재활용 마이컬슨 간섭계^DRMI를 PSL의 적외선 레이저 파장으로 공진이 되도록 안정화되었습니다.

이중 재활용 마이컬슨 간섭계는 간섭계의 각 모서리에 있는 5개의 광학 장치(출력 및 신호 재활용 거울, 빔 스플리터, 암-공진기의 입력 테스트 질량(ITM, 거울))로 구성되며, 최종 테스트 질량(ETM, 거울)은 포함되지 않습니다.

그림 6은 이중 재활용 Michelson 잠금 중 간섭계 구성을 보여줍니다.  암의 길이가 녹색 파장으로 안정화하는 동안 모서리 광학 거울들은 의도적으로 약각 오-정렬됩니다. 그런 다음 녹색 안정화의 정보를 사용하여 암이 의도적으로 PSL 레이저의 적외선 공진을 차단합니다. 마지막으로 3f-PDH 잠금 기술^{PDH-기술의 응용으로 RF 위상변조의 변조주파수의 3차 하노닉 신호(1차 하모닉 신호의 2차 미분에 비례)를 복조신호로 사용하여 안정화 하는 기술}을 사용하여 세 모서리 간섭계의 자유도(Michelson 길이, 전력 재활용 길이 및 신호 재활용 길이)를 동시에 제어합니다.^{[6, 7]} 간섭계 암이 적외선 광(보조 레이저 532 nm 와 1,064 nm 광도 같이 공진)에 대한 공진 상태가 되면 일반적인 1f-PDH 잠금 신호^{변조주파수의 1차 하노닉 신호를 복조신호로 사용하여 안정화 하는 PDH-안정화 기술}가 같은 반전 제어신호로 1,064 nm의 사전안정화레이저로 간섭계 모서리의 광학계를 제어할 수 없게 됩니다. 그러므로, 3f-PDH 잠금 신호는 부호 반전^{암길이 안정화에 사용하였던 1f-PDH 복조 신호와는 부호 반전}으로 인해 영향을 받지 않으며 암이 보조 레이저와 공진 상태에 있는 동안에도 제어를 유지하는 데 사용됩니다.

좀 더 광주파수 관점에서 엄밀하게 기술하면, 암-공진기의 길이가 보조 레이저의 녹색 주파수 광(f_AL(532nm))으로 1f-PDH 제어신호를 이용하여 안정화되어 있으며, 암-공진기 길이에 공진되는 보조 레이저 광과는 약간 다른, 보조 레이저 적외선(f_AL(1.064nm))에 옵셋주파수(f_offset)가 더해진 주파수가 PSL의 적외선 주파수(f_PSL)가 되므로, PSL 레이저 광은 암-공진기와 길이에 공진이 되지 않게 유지되고, 각 모서리 공진기들의 자유도는 암-공진기와 독립적으로 PSL 레이저에안정화할 수 있습니다.

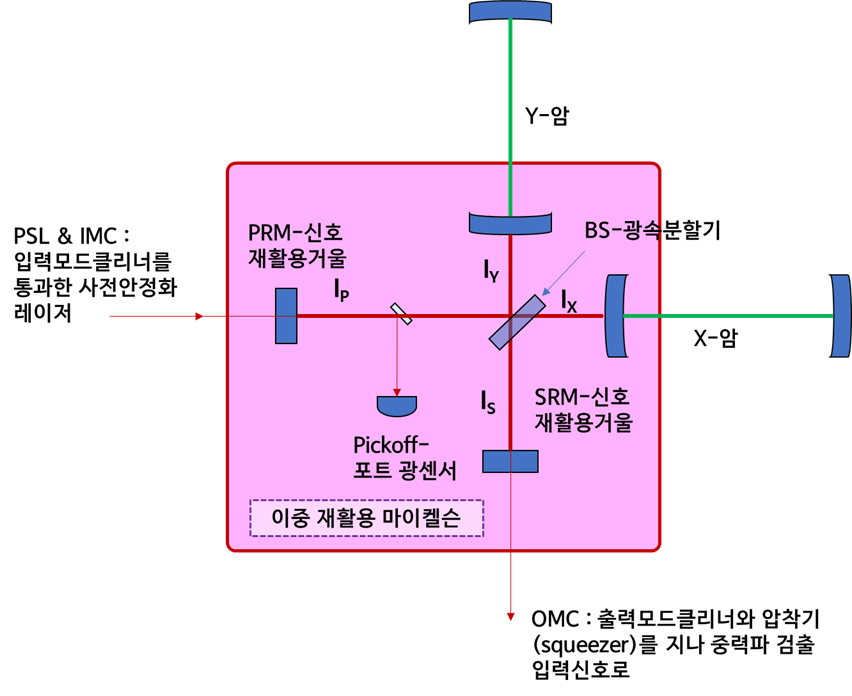
그림7 에서 이중 재활용 마이켈슨은 분홍색 상자에 표시되어 있습니다. DRMI에서는 Michelson 길이(MICH, ()), 신호 재활용 공동 길이(SRCL, ) 및 전력 재활용 공동 길이(PRCL,)의 세 가지 길이 자유도가 있습니다. 픽오프 포트의 광센서는 모든 자유도를 감지하는 데 사용됩니다. 각 자유도는 서로 다른 공동에서 공진하는 서로 다른 위상 변조 측대역 주파수를 통해, PSL의 적외선 주파수() 레이저 광에 공진이 되도록 감지되고 제어됩니다^[8].

그림 7. 잠금 획득의 두 번째 단계: 이중 재활용 Michelson 길이 들의 안정화

이상에서, 2018년 이후 중력파 검출에 사용된 압착된 진공의 간섭계에로의 인적션을 이용하여 민감도가 개선된 고급+라이고에 사용된 암-공진기와 이중 재활용 Michelson 간섭계의 길이 안정화와 중력파 검출 신호에 대해 기술하였습니다.^[9]

광학 정렬 감지 및 제어

광학계의 정렬을 위해 제어해야 할 10개의 자유도를 갖는 암 공진기 거울의 잔류 각도 운동의 정렬 잡음효과를 적절히 제어하기 위해서는 광학계의 정렬오차는 1 이하로 제어되어야 합니다.^[10] 다양한 광검출기를 이용하여 PDH-기술을 사용하에 정렬 제어를 하게 됩니다.

테스터 질량의 열보상

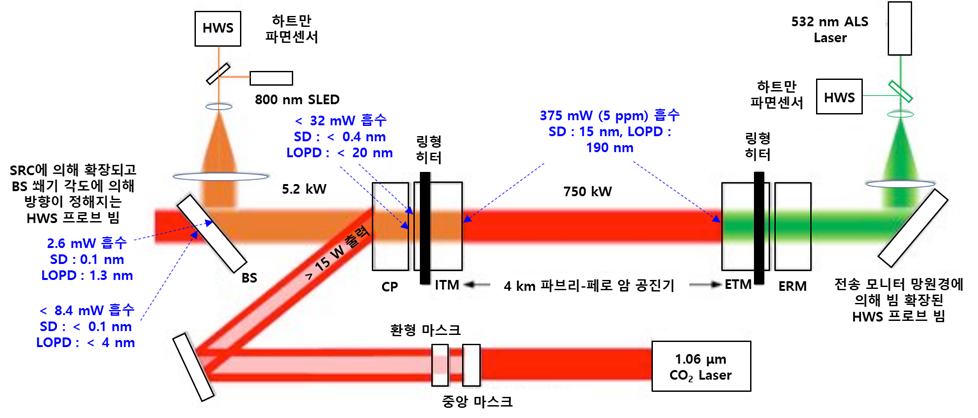
핵심 광학에서 가우시안 프로파일 레이저 빔의 흡수는 열 광학 및 열탄성 효과를 통해 파면 수차로 이어지는 불균일한 온도 증가를 유발합니다. 열 수차는 모든 광학계에서 어느 정도 발생하지만 테스트 질량 광학에만 능동 보정이 필요할 것으로 예상됩니다.

출력 재활용 공진기 안에서 5.2 kW, 암 공진기 안에서 750 kW의 레이저 출력이 거울 사이를 왕복, 공진을 하고 있습니다. 상당한 출력 흡수의 유일한 위치는 테스트 질량 고반사율 표면(750 kW의 5 ppm, 375 mW 출력을 흡수)이며, 가장 큰 광학 왜곡은 테스트 질량 기판의 결과적인 열 렌즈효과로 나타냅니다. ITM 열 렌즈는 주로 재활용 공동의 RF-측파대 모드에 영향을 미칩니다. 반송파 모드는 암 공진기에 의해 시행되며 ITM 렌즈에 의해 훨씬 덜 교란됩니다.

열탄성 팽창으로 인한 테스트 질량 표면 왜곡은 기판 렌즈 왜곡보다 약 10배 작지만, 고출력에서는 상당히 커집니다. 보정되지 않은 표면 왜곡은 ITM 및 ETM 곡률 반경(각각 1,934 m, 2,234 m)을 수 10 m 증가시켜 각 테스트 질량의 빔 크기를 약 10% 감소시킵니다. 이렇게 하면 코팅 면의 열잡음이 증가하고 암 공진기와 재활용 공진기 모드 간의 결합 효율성이 감소합니다.

그림 8. X-암 테스터 질량(거울)의 열 보상 시스템의 개략도

CP : 보상판, SRC:신호재활용공진기, HWS:하트만 파면센서, BS:광속분할기, SLED: 초발광 LED, ALS : 암-길이안정시스템, 그림에서 푸른색 숫자는 각 부분에서의 레이저광 흡수량 및 SD : 표면왜곡, LOPD : 열렌즈효과에 의한 광경로 왜곡을 나타낸다. 위상판 CP에 입력 CO2 레이저 출력(최소 15 W)으로 열 보상하며, 테스터 질량에는 링형 히터로 열 보상한다. SLED 프로브 빔이 BS를 통해 X-암에 전송되며, 유사한 구성이 Y-암에 구현됩니다. 각 마스크는 빔 경로에서 독립적으로 넣거나 빼낼 수 있습니다. 가장 많은 흡수가 일어나는 부분은 ITM/ETM의 고반사율-코팅이 된 면인데, 공진기 내부 출력 750 kW의 5 ppm을 흡수하여 375 mW 출력이 흡수될 것으로 예상한다. 이로 인해 열탄성 팽창으로 인한 테스트 질량 표면 왜곡은 기판 렌즈 왜곡보다 약 10배 작지만 고출력에서는 상당히 커집니다. 보정되지 않은 표면 왜곡은 ITM 및 ETM 곡률 반경을 수 10 m 증가시켜 각 테스트 질량의 빔 크기를 약 10% 감소시킵니다.

이와 같은 문제를 보상하기 위하여 그림 7에서 보는 바와 같이 3가지 장치가 도입되었습니다. 이들은 열복사를 이용하는 링 히터^{RH, Ring Heater}, 레이저 프로젝터^CO2P 및 Hartmann 파면 센서^{HWS, Hartmann Wavefront Sensor}의 세 가지 주요 요소로 구성됩니다.

RH는 ITM 및 ETM의 표면 변형을 보정하고 ITM 기판 열 렌즈를 부분적으로 보정하는 데 사용됩니다. 는 RH에 의해 보정되지 않은 잔류 ITM기판 왜곡을 보정하는 데 사용됩니다. HWS는 테스트 질량의 열 수차를 측정하는 데 사용됩니다. RH와 조합의 기본 목적은 열을 추가하여 메인 빔 가열에 의해 형성된 열 렌즈에 공액 수차를 형성하는 것입니다. RH 출력 안정성은 테스트 질량에 대한 직접 작동을 허용할 만큼 충분히 좋은 반면, 는  레이저 잡음의 영향을 제한하기 위해 보상판^CP에서 작동합니다.

산란광 제어

입력 레이저 광의 상당 부분이 다양한 광학 장치의 산란 또는 반사를 통해 간섭계 모드 외부로 나옵니다. 이 빛은 일반적으로 매달린 광학 장치만큼 기계적으로 잘 격리되지 않은 표면에서 부딪히고 산란되어 주 간섭계 레이저 빔에 입사하여 큰 위상잡음을 만듭니다. 이를 위한 중요한 해결 방법으로는 산란광을 주 광로 이외의 부분에서 차단하는 광차단 판인 배플을 필요한 부위에 설치하는 것으로 가장 중요한 배플 구성 중 하나는 암 공진기 중간 중간에 설치한 배플입니다.

출력 모드 클리너와 중력파 신호 판독법

그림 9. 용융 실리카 브레드 보드크기: 45 cm∙15 cm∙4.1 cm위의 출력 모드 클리너^OMC

OMC(출력 모드 클리너)는 비대칭, AS 포트에서 나오는 모든 RF-측파대 및 고차의 횡모드 광을 필터링하여 중력파 신호를 전달하는 기본 모드만 수신하도록 설계되어 검출기에서 ​​검출해야 하는 출력을 크게 낮추어 신호대잡음비를 줄일 수가 있습니다.

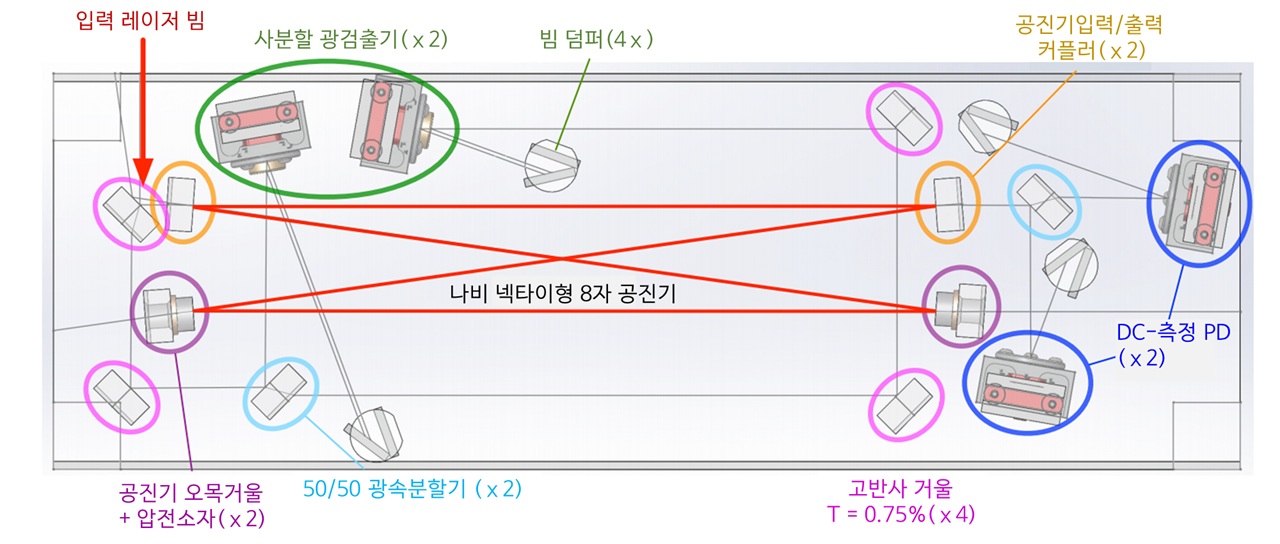
그림 9과 같이 OMC는 RF측대파를 필터링하기 위한 좁은 대역폭과 높은 투과 효율(> 95%)을 고려한 피네세 400(왕복 길이: 1.13 m)를 가진 모드 매칭^{4개 거울 반사면에서 파면 곡률반경과 위상이 레이저 빔의 TEMoo 모드와 일치}된 8자 공진기입니다. OMC의 모드의 주파수 간격은 간섭계 AS포트로 나갈 가능성이 있는 레이저 고차 횡모드 간격과의 일치를 피하기 위해 OMC 공진기 길이가 미세 조정됩니다.

OMC와 광검출기들은 모두 온도 안정성이 좋은 용융 실리카의 단일 브레드보드에 장착되어 OMC 출력 빔과 검출기 사이의 상대적인 움직임을 최소화하여 잡음의 줄입니다. 브레드보드에는 정렬을 돕기 위한 두 개의 사분할 광검출기와 산란광 차단을 위한 다중 빔 덤프도 포함되며, 4개의 거울 중 두 개의 OMC 거울은 공진기의 길이 제어를 위해 PZT 액추에이터에 장착됩니다.

OMC 공진기는 dither 방식으로 AS포트 검출 빔에 공진주파수가 안정화 됩니다. PZT 중 하나는 수 kHz의 주파수에서 공진기 길이에 작은 변조를 하고 광검출기(DC-판독 PD)의 검출 신호는 dither 주파수에서 복조되고 복조된 오차신호는 공진을 유지하기 위해 다른 PZT로 피드백됩니다. 진동 차단을 위해 전체 브레드보드는 능동적 댐핑 및 위치 및 방향 포인팅 기능이 있는 2단계 서스펜션에 장착됩니다. OMC 서스펜션은 HEPI 플랫폼의 HAM 진공 챔버 내에 장착됩니다.

AS 포트 빔은 3개의 조향 광학 장치에 의해 OMC로 향합니다. 이 광학 장치는 OMC에 모드 매칭을 제공하며 진동 격리 및 정렬 포인팅 제어를 위해 능동적 단일 스테이지 서스펜션에 장착됩니다. OMC로 빔의 정렬 최적화 및 제어를 위한 몇 가지 가능한 방식이 있습니다. 간단한 방법은 정지된 조향 광학 장치를 사용하여 AS 포트 빔의 포인팅 방향을 dithering하고 dither 주파수에서 OMC 전송 신호를 복조한 신호를 이용하여 정렬 제어하는 것입니다.

중력파 신호의 판독은 DC-판독법[7]과 함께 출력모드클리너를 사용하여 수행됩니다.이 방식에서는 그림 4에서 설명한 바와 같이 암-공진기들의 공진에서 약간 옵셋(12 pm(10^-12 m) 정도)을 주어 로컬 발진기 필드를 생성하도록 하여 마이켈슨의 어두운 간섭무늬에서 약간 떨어지도록 끌어당겨 놓습니다.

DC-판독법에서의 검출 신호는 변조 없이 직접 마이켈슨 간섭에서 신호에서 얻는 방법인데 RF-헤테로다인 판독과 비해 많은 기술적 잡음 결합에 덜 민감하지만, 산탄 잡음이 제한된 주파수에서 RF-판독값 보다 신호 대 잡음 비가 (3/2)^0.5 만큼 근본적인 개선이 됩니다. GEO600 검출기에서 먼저 더 낮은 양자 잡음을 관측한 이후, 또 압착된 빛의 미래 사용과의 호환성이 있음을 알게 되어, 초기의 라이고 이후의 개선된 라이고나 고급 라이고, 압착된 광을 사용하는 최근에 고급 라이고 모두 이 DC-판독법을 이용하고 있습니다^[12,13]

두 블랙홀의 병합과정에서 발생한 중력파의 최초 신호검출

이와 같이 미약한 변형을 측정한 두 라이고의 검출기가 두 블랙홀의 병합 과정에서 발생한 일시적인 중력파 신호를 최초로 검출하고 그 연구한 결과들을 요약한 대표적인 그림들이 논문에 소개되었습니다.^[14]

관측된 블랙홀은 적색편이 z = 0.09^[15]에 해당하는 410 Mpc의 광도 거리 13.4 광년^[16]에 있습니다. 소스 프레임에서 초기 두 블랙홀 질량은 각각, 36 M⊙(M⊙ : 태양 질량^[17]), 29 M⊙이고, 전체 질량은 65 M⊙, 최종 블랙홀 질량은 62 M⊙이며, E = 3.0 M⊙c² 의 에너지 즉, 3.0 태양 질량의 에너지(E ≅ 5.4 × 10⁴⁷ J)가 중력파로 방출되었슴이 밝혀졌습니다. 그것은 중력파 신호로 한 쌍의 블랙홀의 나선 회전^Inspiral 및 병합^Merger과 단일 블랙홀으로 안정화 단계인 링다운으로 이어지는 과정을 보여주었습니다.

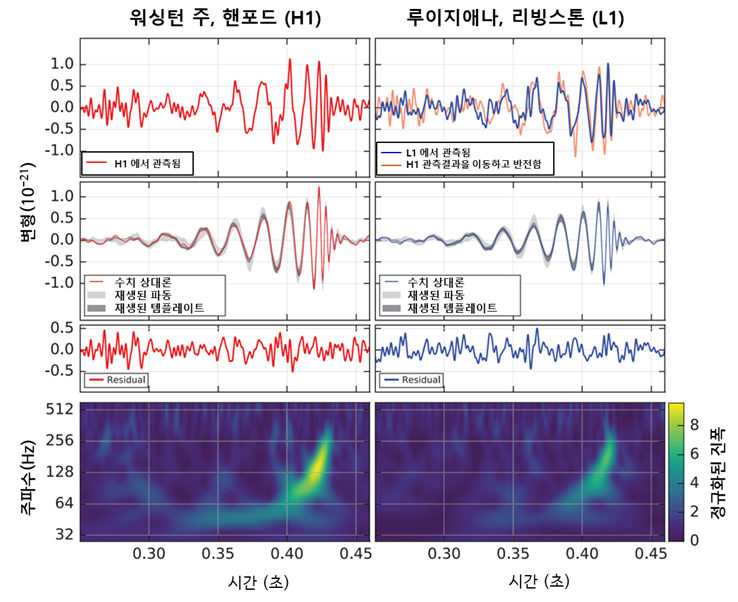
그림 10에서는 최초 검출 중력파^GW150914 신호 검출데이터를 나타낸 그림이며, GW150914는 미국 남동쪽의 리빙스톤 관측소^L1에 6.9 ms 먼저 도착하였고 핸포드^H1 관측 신호와는 위상이 반전되어 있습니다. 이는 두 검출 간섭계의 서로 수직한 X-암 공진기와 Y-암 공진기의 상대 방향이 반대이기 때문입니다. 두 번째 행의 실선은 측정과 일치하는 매개변수를 가진 시스템에 대한 수치 상대론 파형을 보여줍니다. 음영 영역은 두 개의 독립적인 파형 재구성에서 90% 신뢰할 수 있는 영역을 나타냅니다. 세 번째 행은 필터링된 검출 신호에서 필터링된 수치 상대론적인 파형을 뺀 후의 잔여 잡음을 나타냅니다. 하단의 행은 시간에 따라 증가하는 중력파 신호 주파수를 보여주는 변형 데이터의 시간-대-주파수 표현입니다.

그림 10. 라이고 핸포드(H1, 왼쪽) 및 라이고 리빙스턴(L1, 오른쪽) 검출기에 관측된 중력파 GW150914 윗줄 왼쪽: H1 에서 관측된 변형. 윗줄 오른쪽: L1 변형. GW150914는 미국 남동쪽의 L1에 6.9 ms 먼저 도착하였고 H1 신호는 반전되어 있습니다. 두 검출 간섭계의 서로 수직한 X-암 공진기와 Y-암 공진기의 상대 방향이 반대이기 때문입니다. 두 번째 행의 실선은 측정과 일치하는 매개변수를 가진 시스템에 대한 수치 상대론 파형을 보여줍니다. 음영 영역은 두 개의 독립적인 파형 재구성에서 90% 신뢰할 수 있는 영역을 나타냅니다. 세 번째 행은 필터링된 검출 신호에서 필터링된 수치 상대론적인 파형을 뺀 후의 잔여 잡음입니다. 하단 행은 시간에 따라 증가하는 중력파 신호 주파수를 보여주는 변형 데이터의 시간-대-주파수 표현입니다.

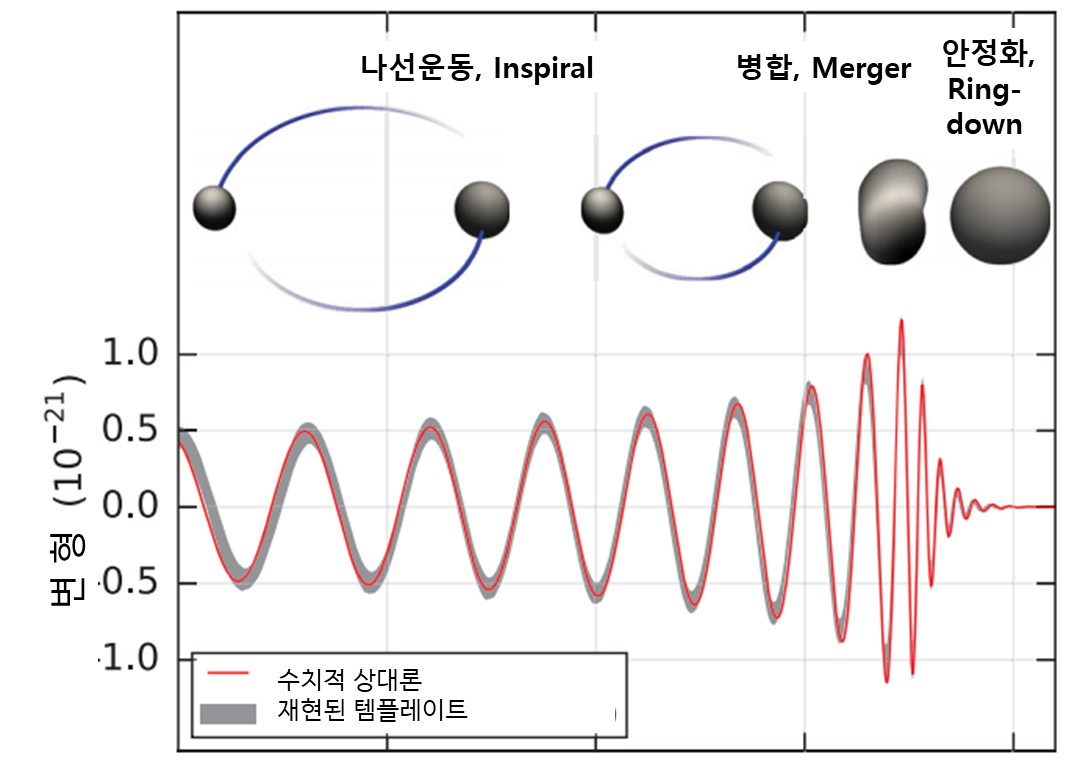
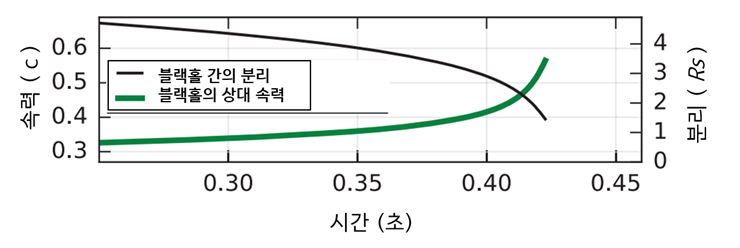
그림 11. 에는 H1에 투영된 GW150914의 추정된 중력파 변형 진폭(상단)을 나타내었습니다. 필터링 없이 파형의 전체 대역폭을 보여줍니다. 위에 삽입된 이미지는 쌍성 블랙홀이 합쳐질 때 블랙홀 지평선의 수치 상대론 모델을 보여줍니다. 하단은 슈바르츠실트 반지름(RS = 2GM/c²)^{블랙홀이 되기 위한 어떤 물체의 반지름 한계점} 단위의 케플러식 유효 블랙홀 분리 및 포스트 뉴턴 매개변수 에 의해 주어지는 유효 상대 속력, 여기서 f는 중력 수치 상대론으로 계산된 파동 주파수이고 M은 전체 질량입니다.

그림 11. H1에 투영된 GW150914의 추정된 중력파 변형 진폭(상단).

필터링 없이 파형의 전체 대역폭을 보여줍니다. 또 삽입된 이미지는 쌍성 블랙홀이 합쳐질 때 블랙홀 지평선의 수치 상대론 모델을 보여줍니다. 하단은 슈바르츠실트 반지름(RS = 2GM/c²) 단위의 케플러식 유효 블랙홀 분리 및 포스트 뉴턴 매개변수 에 의해 주어지는 유효 상대 속력, 여기서 f는 중력 수치 상대론으로 계산된 파동 주파수이고 M은 전체 질량입니다.

중력파 변형 신호 교정^[18]

간섭계 응답 기능의 오차는 중력파를 검출하는 능력과 검출된 중력파 신호의 소스 속성을 측정하는 능력을 저하시킵니다.^[19]그러므로 정확한 검출을 신뢰할 수 있도록 중력파 신호의 교정이 필요합니다. 교정의 정확도는 당연히 검출보다 중력파 소스 매개변수의 정확한 추출에 더 중요합니다. 2σ 신뢰 수준에서 진폭 5% 및 타이밍 16 μs으로 교정 정확도 요구 사항을 설정했습니다. 이것은 강한 쌍성 블랙홀 신호의 검출을 위한 요구 사항과 일치합니다.^[10]

중력파 신호의 진폭 및 주파수의 정확도 등에 대한 교차 교정 검사를 하기 위해 다음과 같은 세 가지 교정 방법이 사용됩니다.
(a) 자유 스윙 Michelson 간섭^[21]
(b) 주파수 변조^[22]
(c) 광자교정기^[23,24,25]

자유 스윙 Michelson 방법에서 간섭계 레이저 광은 테스트 질량을 자유롭게 움직이거나 강제적으로 수 μm의 움직일 때 Michelson 간섭무늬를 교정하기 위한 길이 기준으로 사용됩니다. 이 방법은 10^-12 m 정도의 드라이브 진폭으로 최종 테스터 질량^ETM의 동작시키고 동작 신호의 진폭을 교정합니다.

두번째의 주파수 변조 방법은 단일 암 공진기에 적용하여 교정합니다. 이 구성에서는 알려진 레이저 주파수(f) 변조(Δf)와 등가의 길이 변조(ΔL = -L∙(Δf/f))의 관점에서 공진기 길이 변화 검출 신호를 교정합니다. 약간 다른 주파수에서 최종 반작용 질량 ERM 액추에이터(10^-14 m)를 동시에 구동하여 작동량을 교정하여 ETM의 주파수 반응 동작량을 교정합니다.

세 번째 방법은 광자의 복사압을 이용하여 교정하는 광자 교정기^{Photon calibrator, Pcal} 입니다. 보조의 출력 변조된 레이저를 사용하여 ETM 표면에서 광자 반동을 통해 변위를 생성합니다. ETM거울 중심에서 대칭으로 옵셋된 두 개의 빔이 사용됩니다(그림 12). 오프셋은 광자 압력으로 인한 탄성 변형을 유발하기 때문에 주 간섭계 빔의 위치에서 멀리 이동시키고 2개 빔의 대칭적으로 사용하여 토크(torque, 회전모멘트) 발생을 방지합니다.

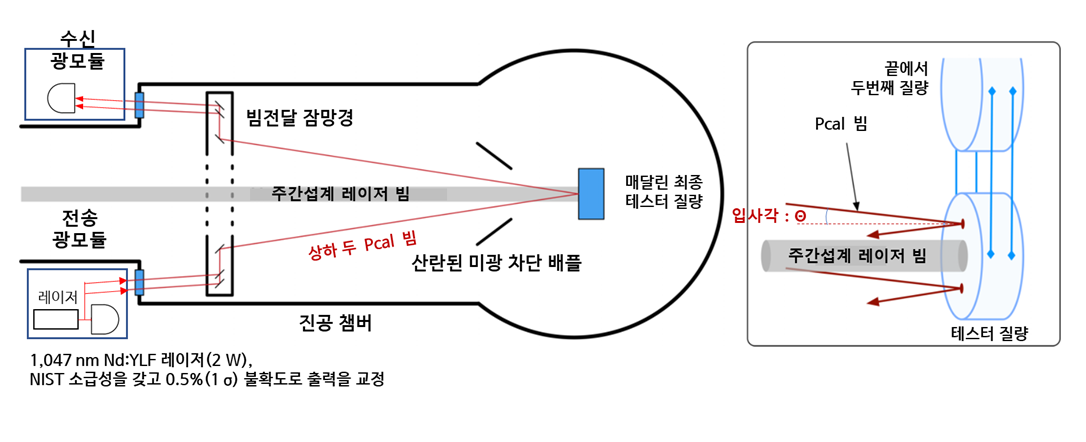
그림 12. 고급 라이고의 광자 교정기 Pcal^[25]

레이저광 송신 모듈에는 레이저, AOM 출력변조기 및 빔 컨디셔닝 광학 장치가 포함되어 있습니다. 진공 잠망경 구조는 미광 배플링에 의한 봉쇄을 방지하고 원하는 위치에서 최종 테스트 질량에 영향을 미치기 위해 입력 빔을 중계합니다. 또한 테스터 질량에서 반사된 빔을 수신기 모듈 내부에 장착된 파워 센서에 중계합니다. 오른쪽 그림은 매달린 테스트 질량 표면에 충돌하는 빔의 개략도입니다. 두 Pcal 빔은 테스터 질량 중심 위아래로 대칭적으로 입사됩니다.

레이저 출력은 NIST^{미국 국립표준기술연구소(National Institute of Standards and Technology)}의 교정용 표준에 소급성을 갖는 교정된 적분구에 장착된 온도 안정화 InGaAs 광검출기로 측정됩니다. 레이저는 2 W 연속파 발진의 1,047 nm파장의 Nd:YLF 레이저입니다. AOM은 최대 1 W의 피크-대-피크의 정현파 출력 변조를 가능하게 하여 100 Hz에서 (10^-16 m)rms의 ETM 변위를 생성합니다.

이때, 주파수 f로 출력을 변조한 광을 테스터 질량의 중심에 대칭의 상하 같은 두 방향으로 테스터 질량의 중심에 대칭적으로 입사하고 변조주파수 f에 따른 변위량을 측정하게 됩니다.

광자교정기의 레이저 출력 Pcal을 주파수 f로 변조하여 입사된 광출력 P(f)에 의해 유도된 거울의 길이 변조 x(f)는 다음과 같이 계산됩니다.^[24]

여기서 θ는 테스터 질량 표면에 대한 Pcal 빔의 입사각 θ = 8.8°, c는 빛의 속력, MT은 테스터 질량의 질량, M_T = 39.6 kg 이며, IT는 관성 회전 모멘트, I_T = 0.415 kg·m² 이고, ⃗ 및 는 각각 ERM 중심으로 부터 주 간섭 빔의 중심까지의 변위 벡터, 두 광자교정기 빔의 중심까지의 변위 벡터입니다. S(f)는 매달린 테스트 질량의 힘-길이 전달 함수입니다, 아래 식에서 s(f)의 -값은 광자의 운동 방향과 반대의 방향의 움직임을 나타냅니다. 20 Hz 이상의 주파수에서 고급 라이고 테스터 질량의 사중진자 서스펜션의 경우에는, s(f)는 거울을 자유로이 매달린 강체로 취급하여 근사화할 수 있습니다.

s(f) ≈ -1/[M_T(2πf)²]

는 적용된 Pcal 힘에 의해 유도된 테스트 질량의 회전으로 인한 의도하지 않은 유효 길이 변화량이 됩니다. 이러한 Pcal 힘은 또한 테스트 질량의 로컬 및 벌크 탄성 변형을 모두 유도하여 교정의 불확도를 크게 할 수 있습니다. 이러한 변형의 영향을 최소화하기 위해 광자교정기는 거울 면의 중심에서 대칭으로 배치되고 거울 기판의 자연 진동 모드의 여기를 줄이기 위해 정확하게 배치된 두 개의 빔을 사용한 것입니다.

또한, Pcal 힘이 테스트 질량에 직접 적용되기 때문에 의도된 변조 주파수 이외의 주파수에서 변위 잡음을 최소화하는 것이 중요합니다. Pcal은 변조된 레이저 출력이 설계된 파형과 일치하도록 피드백 제어 루프를 사용하여 레이저의 자유 동작 상대 출력 잡음과 변조의 고차 고조파를 줄입니다.

Pcal 시스템은 고급 라이고에 4개 설치되어 지속적으로 작동하고 있습니다.
각 라이고 관측소에 각각 2개씩 설치되는데 간섭계 암 끝에 있는 X 및 Y 테스트 질량에 하나씩 있습니다. 1% 이상의 정확도로 필요한 기준 변위를 제공하여 중력파 신호의 진폭과 검출기의 주파수 특성을 측정 교정할 수가 있었습니다.

DC-판독 신호의 자동제어 및 신호 교정

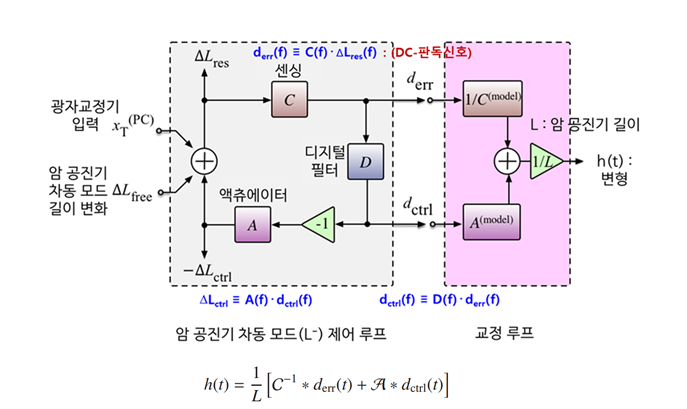
 한편, 검출기의 안정적인 작동을 위해서는 차동 암 길이 자유도(간섭계의 차동 길이 및 각도 자유도와 함께)의 피드백 제어가 필요합니다. 그림 11과 같은 이 피드백 제어는 중력파 GW 판독 신호 d_err(f)의 디지털화된 버전을 취하여 디지털 필터를 적용하여 제어신호 d_ctrl(f)를 생성한 다음, 거울을 변위시키는 테스트 질량 액추에이터 시스템에 제어신호를 전송하여 달성됩니다.

이 제어 시스템이 없으면 변위 잡음 또는 지나가는 GW에서 발생하는 차동 길이 변화는 차동 길이의 억제되지 않은^{free running} 변화 ∆L_free = Lx − Ly = h∙L 를 유발합니다. 여기서 L ≡ (Lx + Ly )/2 는 길이가 Lx 및 Ly 인 각 암 공진기의 평균 길이이고 h는 검출된 변형, h ≡ ∆L_free /L 입니다.

그러나 피드백 제어가 있는 경우 이 free running 변위 ∆L_free는 더 작은 잔류 길이 변화 ∆L_res = ∆Lf_ree(f) / [1 + G(f)] 로 억제됩니다. 여기서 G(f)는 차동 암 길이 서보의 개방루프 전달함수입니다. 따라서 간섭계에 의해 검출된 등가 GW 변형을 추정하려면 이 루프의 효과에 대한 자세한 특성화 및 수정이 필요합니다. 차동 암 길이 피드백 루프의 개루프 전달함수 G(f)는 센싱함수 C(f), 디지털 필터함수 D(f) 및 액츄에이터 전달함수 A(f)의 곱입니다.

G(f) = A(f)∙D(f)∙C(f)

검출기의 센싱 함수 C(f)에 의해 잔류 차동 암 길이 변위가 디지털화된 오차신호로 전달되며. d_err(f) ≡C(f)∙∆L_res(f), 디지털 필터함수 D(f)에 의해 디지털 제어 신호가 디지털 오차신호에서 전달되며. d_ctrl(f) ≡ D(f)∙d_err(f), 액츄에이터의 전달 함수 A(f)에 의해 디지털 제어 신호가 차동 암 길이의 변위를 전달됩니다. ∆L_ctrl ≡ A(f)∙d_ctrl(f), 이러한 관계는 그림 13에 개략적으로 표시하였습니다.

폐루프에서는 그림 13에서 보는 바와 같이 적절한 응답 함수를 적용하여 차동 암 공진기 길이 서보의 제어 및 오차 신호로부터 재구성된 두 암 공동기 길이 사이의 차이에 해당하는 “외부” 차동 길이 변화의 교정된 시계열로부터, h(t)는 다음과 같이 결정됩니다.^[14]

이 추정된 변형 h(t)의 불확도는 광검출기의 센싱 전달달함수 C 및 액츄에이터의 전달함수 A를 특성화하는데 달려 있습니다. 즉, 광자 교정기나 기타 교정법을 이용하여 광검출기의 센싱 및 액츄에이터 전달함수를 포함한 교정 결과에 따라 h(t)의 불확도가 결정됩니다.

그림 13. 암공진기 차동 모드 제어 서보의 블록 다이어그램과 변형값, h(t)의 모델,

광검출기의 센싱, 디지털 필터 및 액츄에이터 등의 전달 함수가 결합되어 개방 루프 전달 함수 G( f ) = A( f )∙D( f )∙C( f )가 되고, 폐회로에서 ΔLfree는 잔류 오차신호 ΔLres = ΔLfree / [1+G(f)]로 크기가 억제됩니다. 신호 XT(PC)는 광자교정기에 의한 테스터 질량의 변조된 변위를 나타냅니다. 여기서 h(t)는 제어 루프에서 얻어지는 변형이며, A와 C-1은 A와 C의 주파수 도메인 모델에서 생성된 시간 도메인 필터이고 ⁎ 는 컨벌루션을 나타냅니다. 이 추정된 변형 h의 불확도는 각 검출기 C 와 A의 센싱 및 액츄에이터의 전달함수를 특성화하는데 달려 있습니다. 즉, 센싱 및 액츄에이터 전달함수를 포함한 교정 결과에 따라 h(t)의 불확도가 결정됩니다.

이와같은 교정 과정에서 의미 있는 불확도는 다음과 같습니다.

NIST의 소급성을 갖는 레이저 출력 교정 불확도는 0.5 %, 자체 야기 테스터 질량의 회전에 의한 불확도는 0.4 %, 반사 광로 측정 불확도는 0.4 %로서 이들을 종합한 광자교정기 X_T(PC)(f)의 전체 불확도는 (1 σ)에서 0.8 %였습니다. 또 광자교정기를 각 센싱 모델 및 액츄에이터 모델 전달 함수와 함께 h(t)를 교정한 결과, 전체 중력파 검출 변형의 감도의 불확도는 검출 대역 20 Hz에서 1 kHz사이에서 관측 데이터의 진폭 측정불확도는 10 %, 위상 측정불확도는 10°입니다. 아울러, GPS-타임 스템핑된 두 라이고의 사이트 데이터의 타이밍 측정불확도는 10 μs이내 입니다.

교정불확도는 ‘GW150914’와 같은 이벤트와 관련된 소스 매개변수의 추정에 직접적인 영향을 미칩니다. 중력파의 진폭은 소스의 광도 거리와 두 블랙홀의 궤도 기울기에 따라 달라지므로 광자교정기에 의해 결정되는 교정의 진폭의 불확도는 광도 거리 추정에 직접적인 영향을 미칩니다. 그러나 광도 거리는 또한 쌍성 소스의 궤도 기울기에 크게 의존하며, 이는 거의 함께 정렬된 두 개의 고급 라이고 검출기에 의해 제한되지 않습니다. 따라서 신호 진폭의 10% 측정 불확도는 ‘GW150914’에 대한 광도 거리의 정확도를 크게 떨어뜨리지는 않습니다. 또, 절대 스케일은 주 레이저 파장을 기준으로 하는 것과 무선 주파수 변조를 기준으로 하는 두 가지 추가 보정 방법으로 교차 확인되었습니다.
각 방법은 절대 척도의 총 불확도 추정치와 비교할 수 있는 두 검출기의 10% 수준에서 척도를 확인할 수 있었습니다. 이와 같은 교정 절차에 의해 중력파 검출 신호에 대한 신뢰성을 확보할 수 있게 된 것입니다.

정 리

 이상에서 인류가 만든 가장 정교하고 복잡하며 정밀한 과학 측정기기 중 하나인 거대한 라이고 시스템이 어떻게 동작하여, 지극히 미세한 중력파 신호를 검출하였는지와 검출기의 성능을 보증할 간섭계의 중력파 변형 값에 대한 교정에 대해 살펴보았습니다.

거대한 라이고는 안정성 및 다양한 잡음에 대한 취약한 것이 특징입니다. 이러한 라이고의 구조와 설계의 정교함에도 불구하고 라이고의 가장 큰 도전과 위협은 인간이 단순히 통제할 수 없었던 환경적 요인에서 비롯되는데 이를 극복하고 성공적으로 중력파 검출하고 또 그 변형의 정확성을 보여주었습니다.

레이저 간섭계 중력파 검출을 위한 40여 년간의 위대한 여정은, 1.5조 원의 거대한 연구비의 지원으로 천문학 분야는 물론이겠거니와 초정밀 계측 분야에 있어서 특히, 간섭계와 레이저 광주파수 제어 및 진동 제어 분야에서의 학문을 더 깊고 풍성하게 한 수많은 아이디어를 발굴하였고, 이를 종합하여 검출기의 민감도와 측정 대역폭을 개선하는 지속적인 진화 과정이였습니다.

이제 ‘중력파 천문학’이라고 하는 새로운 학문이 열리고 많은 호기심과 함께, 세계의 더 많은 젊은 학자들이 동참하여 중력파 검출기들은 더 빠르게 진화, 발전하고 있습니다.
우리의 많은 젊은이들도 이 위대한 여정에 동참하여 우주에 대한 많은 호기심을 풀 기회가 이 땅에서도 마련되길 기대해 봅니다.

길이 측정표준과 관련하여 레이저 주파수 제어계측 연구를 오랫동안 하면서도 몰랐던, 레이저 간섭계 중력파 검출에서의 지대한 역할을 하신, 바이스 박사님와 킵손 박사님과 함께 라이고의 공동 창립자의 한 사람이였던, 작고 큰 과학자 R. 드레버 박사님 ^{2017년 봄에 작고하시어, 그해 가을의 중력파 검출에 대한 노벨물리상을 수상하지 못하였습니다.}의 업적을 기리며 글을 마칩니다.

그동안 본 웹진에 기획 연재된 ‘측정과학’의 일부분으로 게재되었던, 본 아티클을 포함하여 많은 분량의 글들인, ‘미터의 정의와 레이저’, 나노계측학을 위한 X-선 간섭계와 실리콘 격자상수‘, ’레이저 간섭계 중력파 관측소(라이고, LIGO)의 레이저 간섭계‘를 큰 용기와 아량으로 끈기 있게 읽어 주신 독자 여러분께 감사의 말씀을 드립니다.

아울러, ’과학의 지평‘의 편집진 여러분께도 감사의 말씀을 드립니다.

참고 및 문헌

[1] Scott Ransom, The State of Gravitational Wave Detection with Pulsar Timing Arrays – ppt download (slideplayer.com),
[2] Aasi J et al (LIGO Scientific Collaboration) (2015) Class Quantum Grav 32:074001. arXiv:1411.4547
[3] Fritschel P, et. al., Appl. Opt. 40, 28, 4988, 2001
[4] J. Mullavey, et.al., Optics Express, Vol. 20, Issue 1, pp. 81-89 (2012), arXiv:1112.3118 [physics.ins-det]
[5] K. Izumi et al., J. Opt. Soc. Am. A, Vol. 29, No. 10, 2092, October 2012
[6] Staley, A.; et al. Achieving resonance in the Advanced LIGO gravitational-wave interferometer. Class. Quantum Gravity 2014, 31, 245010.
[7] Arai, K. et al., New signal extraction scheme with harmonic demodulation for power-recycled Fabry-Perot-Michelson interferometers. Phys. Lett. A 2000, 273, 15–24.
[8] Abbott, R.; Adhikari, R.; Ballmer, S.; Barsotti, L.; Evans, M.; Fritschel, P.; Frolov, V.; Mueller, G.; Slagmolen, B.; Waldman, S. Advanced LIGO Length Sensing and Control Final Design. Tech. Rep. 2010, 1000298, 2010.
[9] C. Cahillane, G. Mansell, Review of the Advanced LIGO GRavitational Wave Observatories Leading to Observing Run Four, Galaxies, 2022. 10, 36
[10] Mueller G, 2005 Optics Express 13 7118
[11] S Hild et. al., 2009 Class. Quantum Grav. 26 055012, arXiv:0811.3242 [gr-qc]
[12] Tobin T Fricke, et.al., Class. Quantum Grav. 29 (2012) 065005 (18pp), doi:10.1088/0264, arXiv:1110.2815 [physics.ins-det]
[13] J. Abadie, et. al., arXiv:1109.2295 [quant-ph]
[14] Abbott, B,,P, et. al., LIGO Scientific and Virgo Collaboration, (2016c), Phys Rev Lett 116:061102. https:// doi.org/ 10.1103/ Phys. Rev. Lett. 116.061102
[15] 먼 외부은하들로부터 관측되는 적색편이는 주로 우주 팽창에 의한 우주론적 적색편이로서 먼 은하일수록 큰 적색편이 값을 나타낸다는 허블의 법칙은 우주 팽창의 근거한 것으로, 일반적으로 적색 편이량 z 는 관측하는 원자 복사 스펙트럼 선의 z 값으로서, z = (λ관측파장/λ고유파장)-1 의 관계식을 갖는다. 특정 파장 스펙트럼이 적색 쪽으로 편이되었을 때를 적색편이라 하고 z값은 + 값을 갖으며. 이 z값에 따라 별까지의 거리를 알 수가 있습니다.
[16] 1 Mpc(메가파섹) 은 약 3.08 × 1022 m이며, 약 3.26156 광년입니다. 중력파원까지 이 거리 r은 410 Mpc(메가 파섹) 은 약 1.26 × 1031 m 이며, 또 약 13.37 억광년입니다.
[17] M☉(태양 질량); 태양질량을 나타내는 천문학에서의 특수 단위이며, M☉ = (1.98847 ± 0.00007) × 1030 kg의 값을 갖습니다.
[18] B. P. Abbott, et. al., “Calibration of the Advanced LIGO detectors for the discovery of the binary black-hole merger GW150914“, arXiv:1602.03845 [gr-qc]
[19] Lindblom L, et.al., “The Advanced LIGO photon calibrators” 2009 Phys. Rev. D 80 042005
[20] Lindblom L, “Optimal calibration accuracy for gravitational-wave detectors“, 2009 Phys. Rev. D 80 042005
[21] J. Abadie, et. al., “Calibration of the LIGO“, Gravitational Wave Detectors in the Fifth Science Run“, arXiv:1007.3973 [gr-qc]
[22] Goetz E and Savage R L, “Calibration of the LIGO displacement actuators via laser frequency modulation” 2010 Class. Quantum Grav. 27 215001, arXiv:1005.3746 [gr-qc]
[23] D.A. Clubley, et.al., “Calibration of the Glasgow 10 m prototype laser interferometric gravitational wave detector using photon pressure“, Physics Letters A 283 (2001) 85–88
[24] E. Goetz,et.al., “Precise calibration of LIGO test mass actuators using photon radiation pressure“, arXiv:0910.5591 [gr-qc]
[25] S. Karki, D,, et. al., “The Advanced LIGO photon calibrators,” Review of Scientific Instruments 87, 114503 (2016), arXiv:1608.05055 [astro-ph.IM]

관련기사

– 레이저 간섭계 중력파 관측소(라이고, LIGO)의 레이저 간섭계
– 나노계측학을 위한 X-선 간섭계와 실리콘 격자상수
– 미터(m)의 정의와 레이저