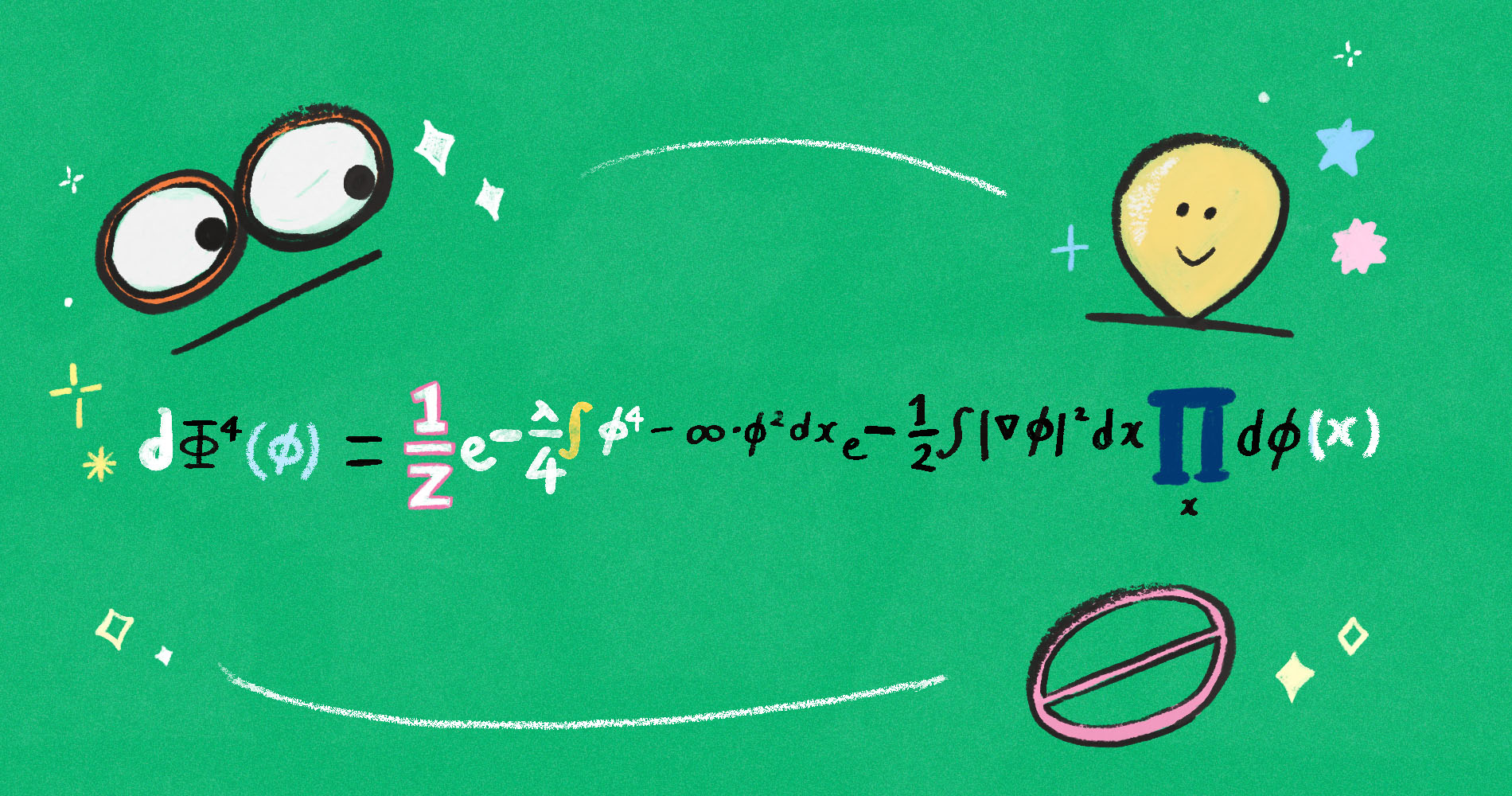편미분 방정식을 이용한 양자장 이론의 건설 [1]: 무한 차원 깁스 측도와 확률 편미분방정식

1. 들어가며

오늘 아침 출근하는 버스에서 이번 학기에 가르치는 확률론 수강생 중 한 학생이 인사를 했는데, 학기가 시작한 지 한 달이 지났음에도 불구하고 그 학생의 이름을 기억하지 못하겠더군요. 이번 학기 수업을 수강하는 학생이 총 90명인데, 각 학생의 이름을 기억하는 것은 물론이고 개개인의 학습 태도를 파악하는 것은 정말 어려운 일 같습니다. 하지만 학생들과 저는 매주 같은 시간에 같은 장소에서 만나고 있으며, 모두가 약속된 날짜와 시간에 함께 시험을 보게 될 것입니다. 즉, 약속된 규칙하에서는 개개인을 모아놓은 전체의 경향성을 예측해 볼 수 있겠죠.

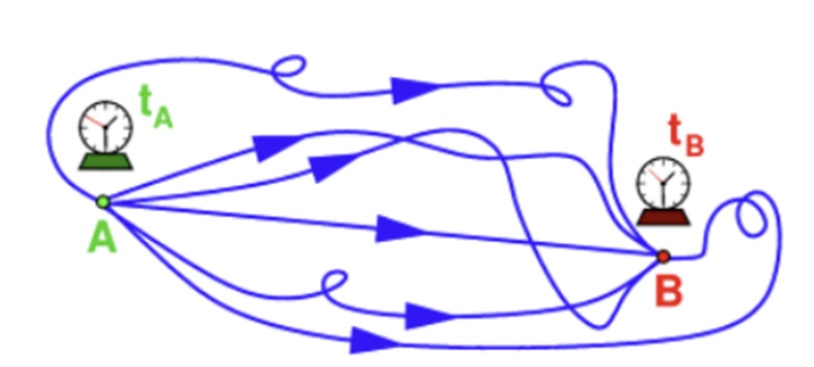
물리학에서 장^field은 시간과 공간의 각 위치마다 다른 값을 갖는 물리적인 양을 말합니다. 장에는 온도를 나타내는 스칼라장, 고전 역학에서의 힘, 속도와 같은 벡터장, 그리고 상대성 이론에서의 텐서장이 있습니다. 20세기부터 모든 물리 현상을 양자역학으로 설명하기 위해 노력해 왔는데, 양자장론은 이전에 사용되던 고전적인 장과 상대론적인 장을 양자이론에 맞게 조정하여 구현하는 것을 목표로 도입되었습니다. 그렇다면 양자역학을 기존 역학 이론에 도입한다는 것은 어떤 것을 의미할까요? 고전역학에선, 물리량의 경로는 초기 조건과 힘이 주어지면 단 하나의 경로로 결정되는 데 반해, 양자역학적으로는 다양한 가능성, 즉 이렇게도 갈 수 있고, 저렇게도 갈 수도 있으므로 이런 무한히 많은 경로를 모두 더해서 생각해 보자는 것이 바로 파인만의 경로적분 ^{path integral} 입니다. 이러한 경로적분을 행하는 데 있어서 필요한 것은 각 경로에 적절한 확률 가중치를 주고서 합해주는 것인데 이때 등장하는 확률이 무한차원 깁스 측도 ^{Gibbs measure} 입니다. 정해진 확률 법칙하에서 많은 경로들의 경향성을 예측하는 것은, 제 수업 수강생들이 매주 약속된 시간과 장소에서는 대부분 나타날 것이라는 기대와 같이, 하나의 공통된 규칙, 즉 깁스 측도 하에서 묶여있다는 사실에 근거합니다.

이번 글에서는 양자장론에서 등장하는 무한차원 깁스 측도를 소개하고 밑에서 주로 설명할 확률적 양자화 ^{stochastic quantization} 를 통해 이러한 무한차원의 대상을 보다 구체적인 방법으로 접근해 보고자 합니다. 확률적 양자화를 한 문장으로 요약해 본다면

양자장론의 무한차원 확률측도는 고전역학 또는 열역학의 법칙들로부터 얻어진 보다 구체적인 확률 편미분방정식을 통해 이해될 수 있다는 것입니다

이러한 확률적 양자화의 개념은 넬슨 ^Nelson과 파리지 ^{Parisi, 2021년 노벨 물리학상 수상자}, 그리고 우 ^Wu에 의해 이미 20세기에 소개가 되었지만, 무한차원 깁스 측도를 설명해 주는 편미분방정식을 푸는 것은 상당히 오랜 기간 미해결 문제로 남아 있었습니다. 이러한 문제는 2010년 중반 이후에 하이러 ^{Hairer, 2014년 필즈상 수상자} 그리고 구비넬리 ^Gubinelli 등에 의해 개발된 기법들을 통해 풀리게 됨으로써 양자장론의 엄밀한 수학적 건설 문제를 편미분 방정식을 활용하여 해결할 수 있는 또 다른 접근법을 제시하게 된 것입니다. 양자장론의 물리적 배경과 관련해서는, 유필상 교수님의 HORIZON 기사 “물리수학: 수학과 물리학의 더욱 놀라운 만남“과 이현민 교수님의 HORIZON 기사 “초중력 이론과 입자 물리학: 2019 Fundamental Physics Prize에 부쳐“를 읽어보시면 도움이 될 것으로 생각됩니다.

2. 깁스 측도와 그것을 보존하는 뉴턴 미분방정식 흐름

개별 대상들이 가지는 궤도, 성질은 제각각이지만 하나의 공통된 확률분포로 묶여있다.

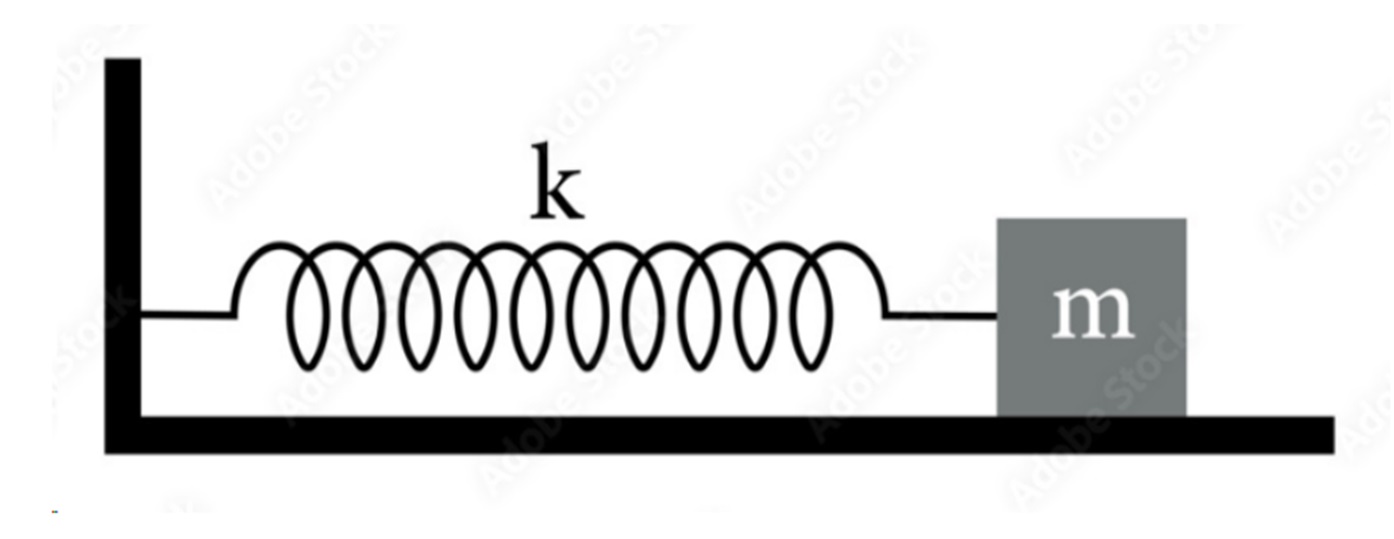
이번 절에서는 깁스 측도에 대한 개념을 이해하기 위해, 고등학교 시절에 학습한 단순 조화 진동자 ^{simple harmonic oscillator} 를 생각해 보도록 하겠습니다. 단순 조화 진동은 평형점을 기준으로 물체의 위치에 비례한 복원력 \(F=-kq \) 외에는 다른 힘을 받지 않으며, 따라서 일직선상에서 주기적으로 일어나는 사인 혹은 코사인 모양의 운동을 보여줍니다. 이 운동을 뉴턴의 운동 방정식에 따라 기술하면 다음과 같이 주어지는데
\begin{align*}
m\ddot{q}(t)=-kq(t) \qquad \text{그리고} \qquad \dot{q}(t)=p(t),
\end{align*}

여기서 \(q(t)\)는 시간에 따른 물체의 위치를 의미하며 \(p(t)\)를 물체의 속도를 나타냅니다. 논의의 편의를 위해 질량과 용수철 상수를 \(m=k=1 \)로 놓고, 위의 뉴턴 미분 방정식을 풀어보면, 그 해는 아래와 같이 표현할 수 있습니다
\begin{align}
\begin{pmatrix}
q(t)\\
p(t)
\end{pmatrix}
=
\underbrace{ \begin{pmatrix}
\cos t & \sin t \\
-\sin t & \cos t
\end{pmatrix} }_{\Phi_t=\text{회전}} 
\begin{pmatrix}
q(0)\\
p(0)
\end{pmatrix}
.   \qquad\qquad                                
\label{rotat} (2.1) \end{align}특히, 위 표현 (2.1)을 통해 우리는 조화 진동자를 통한 운동은 초기위치 \(q(0)\)와 초기속도 \(p(0)\)에 대한 회전운동임을 알 수 있습니다. 운동방정식의 해 표현 (2.1)에 따른다면 초기 위치 \(q(0)\)와 초기 속도 \(p(0)\)가 달라진다면 시간 \(t \)에서 물체의 위치 \(q(t)\)와 속도 \(p(t)\)도
달라짐을 알 수 있습니다. 따라서 초기 상태를 정확히 파악할 수 없거나 혹은 다양한 초기값을 동시에 고려해야 할 때, 뉴턴의 운동 방정식을 사용하여 분석하는 것은 효과적이지 않을 뿐만 아니라 현실적으로 불가능해집니다. 이를 해결하기 위해 물리학에서 특히 통계역학에서, 실현 가능한 많은 개별적 대상을 묶어서 확률분포로 이해하게 됩니다. 이러한 개념을 물리학에선 통계적 앙상블 ^{statistical ensemble} 이라 하며 수학적으로는 깁스 측도 ^{Gibbs measure} 라고 부릅니다.

위에서 살펴본 조화 진동자를 통계적으로 설명해 보도록 하겠습니다. 조화 진동자의 해밀토니안 \(H(q(t),p(t))\), 즉 에너지를 살펴보면, 해밀토니안은 다음과 같이 운동 에너지 \(\frac 12 p(t)^2 \)와 위치 에너지 \(\frac 12 q(t)^2 \)의 합으로 표현됩니다
\begin{align*}
H(q(t),p(t))=\frac 12 q(t)^2+\frac 12 p(t)^2.
\end{align*}

위에서 도입한 에너지를 통해 조화 진동자를 기술하는 통계적 앙상블, 즉 깁스 측도를 도입해 보도록 하겠습니다
\begin{align*}
d\rho_\beta=Z^{-1}e^{-\beta H(q,p)}dqdp, \qquad Z_\beta=\int_{\mathbb{R}^2} e^{-\beta H(q,p)}dqdp.
\end{align*}

여기서 \(\beta^{-1}\)는 온도를 의미합니다. 그러면 이러한 확률 측도는 왜 유용한 대상이 될 수 있을까요?

위에서 살펴본 조화진동자를 설명하는 뉴턴의 운동방정식의 흐름 (2.1) \(\Phi_t:(q(0),p(0))  \mapsto(q(t),p(t))\) 는 초기 상태 \(q(0), p(0))\)를 회전하는 것을 의미합니다. 따라서

• (1) 넓이인 \(dqdp \) 르벡 측도^{Lebesgue measure} 회전 흐름 \(\Phi_t \) 하에서 모든 시간에 대해 보존됩니다.
• (2) 해밀토니안 \(H(q(t),p(t))\)는 위치와 속도의 크기 \(|(q(t),p(t))|^2  =\frac 12 q(t)^2+\frac 12 p(t)^2 \)에만 의존하므로 에너지는 \(H(q(t),p(t))\) 회전 흐름 \(\Phi_t \) 하에서 모든 시간에 대해 보존됩니다.

따라서 이러한 두 가지 사실에 근거해 우리는 깁스 측도가 운동 방정식의 흐름 \(\Phi_t \)를 따라 불변하는 대상임을 보일 수 있게 됩니다. 이를 풀어서 설명하면

초기 상태 \((q(0),p(0))\)를 정확히 알 필요 없이 초기 상태가 깁스 측도로 분포되어 있다면 \(Law(q(0),p(0))=\rho \), 시간 \(t\)에서의 위치와 속도 \((q(t),p(t))\)의 확률 분포 역시 초기 상태의 확률 분포와 같다 \(Law(q(t),p(t))=\rho \). 

따라서 통계 앙상블인 깁스 측도는 위 시스템하에서 시간이 지나도 변하지 않는데, 이는 동역학계나 확률론에서 등장하는 불변 측도 ^{invariant measure}에 해당합니다.

3. 깁스 측도와 백색 소음이 들어간 뉴턴 미분방정식

이번에는 위 조화진동자의 예시에서 보다 좀 더 일반적인 해밀토니안과 확률적 강제력 ^{stochastic forcing}이 추가된 뉴턴 방정식을 생각해 보도록 하겠습니다.

확률적인 강제력을 도입하는 가장 중요한 이유는 기존의 결정론적인 뉴턴 미분방정식으로는 달성할 수 없었던 통계적인 균형 상태를 가능하게 한다는 것입니다. 여기서 통계적인 균형상태는 시간을 충분히 흘려보내면 (\(t\to\infty \)), 뉴턴 방정식의 해가 깁스 측도로 수렴함을 의미합니다.

이전과 같이 시간 \(t \)에서 \(q(t)\)는 물체의 위치를 나타내고 \(p(t)=\dot{q}(t)\)는 물체의 속도를 의미합니다. 그러면 아래 에너지, 즉 해밀토니안에서
\begin{align*}
H(q,p)=\frac 12 |p|^2+V(q)
\end{align*}

오른쪽의 첫 번째 항은 여전히 운동에너지 \(\frac 12|p|^2 \)를 의미하고 두 번째 항은 포텐셜 에너지 \(V(q)\)를 의미하게 됩니다. 이와 관련된 뉴턴의 운동방정식을 적어 보면 다음과 같이 쓸 수 있는데
\begin{align}
\underbrace{\ddot{q}}_{\text{관성력}}=\underbrace{-\bigtriangledown V(q)}_{\text{포텐셜 힘}}-\underbrace{\gamma \dot{q}}_{\text{마찰력}} +\underbrace{\sqrt{2\gamma \beta^{-1}}\dot{W}}_{\text{무작위 힘      }} \qquad
\text{     (3.1)}
\end{align}

이 방정식은 랑주뱅 동역학^{Langevin dynamics}이라고 불리며, 이전 단순 조화진동과는 달리 뉴턴의 운동 방정식에서 다른 힘의 효과를 추가로 고려한 것입니다.

(1) \(-\bigtriangledown V(q)\)는 입자 상호 작용 포텐셜에서 계산된 힘입니다.

(2) \(-\gamma\dot{q}\) 는 마찰력을 의미하며 \(\gamma >0\)는 마찰 계수를 나타냅니다.

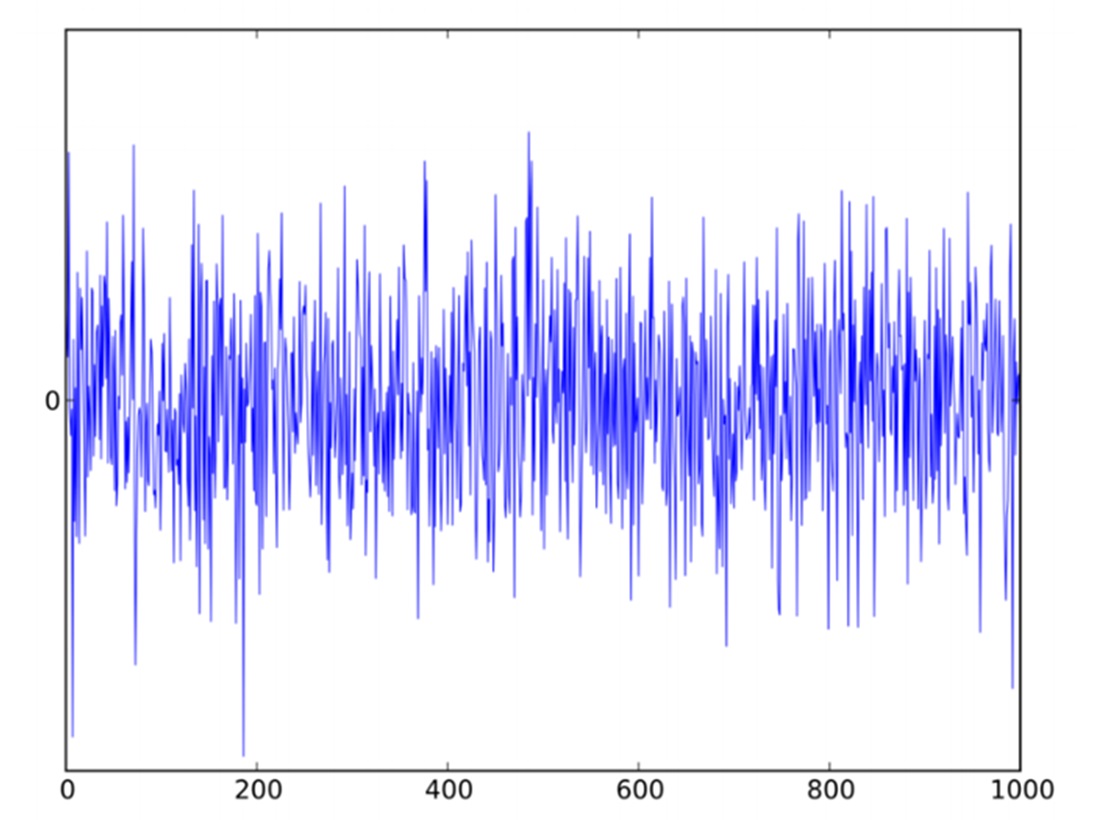
(3) \(\dot{W}\)는 충돌 효과를 나타내는 확률적 강제력, 즉 시간에 대한 백색 소음 ^{white noise}를 의미하며, \(\beta ^{-1}\)는 온도를 나타냅니다. 백색 소음은 그림 2.에서와 보이는 것과 같이 서로 다른 진동수^frequency에서 동일한 강도를 갖는 무작위 신호입니다. 이는 브라운 운동 \(W\) ^{Brownian motion}의 시간 미분으로 이해될 수 있습니다.

중요한 사실은 마찰력과 백색 소음으로 인한 힘들이 추가되더라도, 이전의 단순 조화 진동운동과 마찬가지로 깁스 측도는
\begin{align*}
d\rho_\beta=\frac 1Z_{\beta}e^{-\beta H(q,p)}dqdp, \qquad Z_\beta=\int_{\mathbb{R}^2} e^{-\beta H(q,p)}dqdp
\end{align*}

여전히 뉴턴미분 방정식의 흐름을 따라 불변 측도 ^{invariant measure} 가 됨을 보일 수 있습니다.
\begin{align}
Law(q(0), p(0))=\rho_\beta \qquad \Rightarrow \qquad Law(q(t),p(t))=\rho_\beta \qquad \text{모든 $t$에 대해.
    (3.2)}
\end{align}

더욱이나 새로운 점은 백색 소음 ^{white noise} 의 확률적 강제력 ^{stochastic forcing}과 마찰력으로 인한 감쇠 효과로 인해 에르고딕성 ^ergodicity이 성립한다는 것입니다. 이를 쉽게 표현하면, 초기 확률 분포가 깁스 측도가 아니라고 할지라도 \((Law(q(0),p(0))\neq\rho_\beta)\), 뉴턴 미분방정식의 해가 깁스 측도로 수렴함을 의미합니다
\begin{align}
Law(q(t), p(t)) \qquad \to \qquad \rho_\beta, \qquad \text{$t\to \infty$ 일 때.       (3.3)}
\end{align}

여기서 에르고딕성이 의미하는 바는 초기 값 \(Law(q(0),p(0))\)에 대한 확률 분포가 어떤 것이든 상관없이,  이전의 기억을 완전히 잃으면서, 충분한 시간이 흐르면 확률 미분 방정식 (3.1) 해의 확률분포가 깁스 측도가 된다는 것을 말해줍니다. 지금까지의 설명을 요약해 보자면

(3.3)을 통해, 확률 미분 방정식의 전역 해 global solution를 구할 수 있다면, 깁스 측도가 아주 복잡할 지라도 확률 미분 방정식의 균형상태 \((t=\infty)\)로 이해할 수 있습니다.

이후의 논의에서 위 사실은 중요한 역할을 합니다. 밑에서 설명할 양자장론에서의 확률적 양자화^{stochastic quantization}는 장이론의 여러 공리를 충족하는 깁스 측도를 직접 건설하는 대신 좀 더 구체적인 확률 편미분 방정식의 해를 공부함으로써 장이론에 대한 접근법을 만들어내는 데 의의가 있습니다.

4. 깁스 측도와 브라운 동역학

양자장론을 얘기하기에 앞서 이후 논의를 위해 깁스 측도를 균형상태로 가지는 또 다른 미분방정식인 브라운 동역학 ^{Brownian dynamics}을 잠깐 소개하고 넘어가 보고자 합니다. 이전 절에서 살펴봤던 랑주뱅 동역학^{Langevin dynamics}을 다시 살펴보면
\begin{align*}
\underbrace{\ddot{q}}_{\text{관성력}}=\underbrace{-\bigtriangledown V(q)}_{\text{포텐셜 힘}}-\underbrace{\gamma \dot{q}}_{\text{마찰력}} +\underbrace{\sqrt{2\gamma \beta^{-1}}\dot{W}}_{\text{무작위 힘}}
\end{align*}

마찰의 크기가 증가할수록 \(\gamma\to\infty\) 감쇠 효과가 관성력에 비해 우세해집니다. 따라서 위의 뉴턴 방정식은 마찰의 크기를 극단적으로 증가시킬 때  \(\gamma\to\infty\) 관성을 무시해 버리는 상태가 됨을 짐작할 수 있습니다. 이를 좀 더 정확히 설명하기 위해 마찰력 상수 \(\gamma\)를 사용한 스케일링을 통해 위치 함수 \(q(t)\)를 다음과 같이 변환해 주고 \(q^{\gamma}(t)=q(\gamma t)\) 백색소음 ^{white noise}이 다음과 같은 스케일 변환 \(\dot{W}(\gamma t)=\frac{1}{\sqrt{\gamma}}\dot{W}(t)\)에서 불변한다는 것을 사용하면

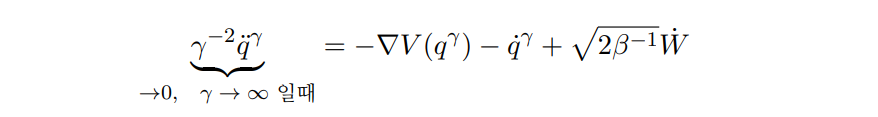
위와 같은 변환된 미분방정식을 얻을 수 있는데, 마찰의 크기가 커질 때 \(\gamma\gg 1\), 관성력 항인 \(\gamma^{-2}\ddot{q}^\gamma\)은 다른 세 항에 비해 무시할 수 있을 정도로 작아지게 됩니다. 따라서 마찰계수를 무한대로 보내서 \(\gamma\to\infty\), 관성효과를 완전히 무시해 버린다면 다음과 같은 브라운 역학^{Brownian dynamics}으로 수렴함이 알려져 있습니다.

마찰의 크기를 극단적으로 무한대로 보낼 때 \(\gamma\to\infty\), 그 결과로 시스템은 관성적인 상태에서 확산 (브라운 운동) 상태로 전이됩니다. 이러한 이유로 브라운 동역학^{Brownian dynamics} 은 관성이 없는 과도하게 감쇠된 랑주뱅 동역학^{overdamped Langevin dynamics}으로도 알려져 있습니다.

이러한 브라운 역학이 중요한 이유는 이전 보통의 랑주뱅 역학^{Langevin dynamics} (3.1)과 같이 확률적 강제력^{stochastic forcing}으로 인한 에르고딕성^ergodicity이 발생한다는 것입니다. 즉, 초기 분포가 무엇인지는 중요하지 않고, 시간이 충분히 흐르면 균형 상태는 결국 깁스 측도가 된다는 것입니다
\begin{align}
Law(q(t)) \qquad\rightarrow\qquad Z_\beta^{-1}e^{-\beta V(q)}dq \qquad \text{$t\to \infty$ 일 때.       (4.2)}
\end{align}

따라서 깁스 측도는 브라운 동역학^{Brownian dynamics}의 균형상태 \((t=\infty)\)로 이해할 수 있습니다.

지금까지의 논의를 요약해 보면 통계적 앙상블인 깁스 측도의 분석은, 두 개의 미분 방정식 (1) 랑주뱅 역학^{Langevin dynamics} (3.1)과 (2) 브라운 역학^{Brownian dynamics} (4.1)을 공부함으로써 행해질 수 있다는 것입니다.

5. 구성적 양자장 이론과 무한차원 깁스측도

도입부에서 언급했던 것과 같이 양자장론은 이전에 사용되던 고전적인 장과 상대론적인 장을 양자이론에 맞게 구현하는 것을 목표로 도입되었습니다. 그렇다면 양자역학을 기존 역학 이론에 도입한다는 것은 어떤 의미일까요? 고전역학에선, 관심 있는 물리량의 경로가 초기 조건과 힘으로 유일하게 결정되는 데 반해, 양자역학적으로는 이렇게도 갈 수 있고, 저렇게도 갈 수 있으므로 가능한 무한이 많은 경로들을 모두 더해서 생각해 보자는 것이 바로 파인만의 경로적분^{path integral} 이라고 언급했었습니다. 경로적분에서 필요한 것은 각 경로에 적절한 확률 가중치를 주고서 합하는 것인데, 여기서 확률 가중치는 우리가 지금까지 살펴봤던 깁스 측도를 사용하게 됩니다.

깁스 측도를 도입하는 방법은 해밀토니안 또는 라그랑지안으로 만들어지는 작용 함수 \(S\) ^{action functional}를 사용하는 것입니다. 고전 물리학은 이 작용 함수의 오일러-라그랑주^{Euler-Lagrange} 방정식을 풀어서 물리량의 유일한 경로를 얻게 된다면, 양자 물리학은 통계적인 성격을 갖고 있기 때문에, 작용 함수 \(S\)를 이용해 다음과 같은 확률인 깁스 측도를 사용하게 됩니다
\begin{align}
\text{무한 차원 깁스 측도}\quad d\rho_{\hbar }=Z_{\hbar}^{-1}e^{-\frac{1}{\hbar} S(\phi) }\prod_{x \in \mathbb{R}^d} d\phi(x), \quad Z_{\hbar}=\int e^{-\frac{1}{\hbar} S(\phi) }\prod_{x \in \mathbb{R}^d} d\phi(x) \label{Gibbs.}  \quad      (5.1)
\end{align}

(5.1)에서 나타나는 \(\hbar\)는 플랑크 상수로서 양자 역학을 설명하기 위한 양자 매개 변수입니다. ¹.  장^field의 개념을 잠깐 다시 짚어보면, 장은 시간과 공간의 각 위치마다 다른 값을 갖는 물리적인 양을 말합니다. 스칼라장 (온도), 벡터장 (힘, 속도), 그리고 텐서장 등은 모두 시간과 공간에 대한 함수 \(\phi(t,x)\)입니다. 따라서 위의 경로적분에 필요한 깁스측도는 점들을 모아놓은 유클리드 공간 \(\mathbb{R}^d\)에서의 적분이 아닌, 장을 설명하는 시공간 함수들을 모아놓은 공간 \(\{\phi:\mathbb{R}^d\to G=\text{게이지 그룹}\}\)² 위에서 적분하게 됩니다. 즉, 경로적분은 함수 공간 위에서의 적분^{functional integral}을 수행하는 것입니다. 따라서 앞의 여러 절에서 살펴봤던 유한차원 깁스 측도에서와는 달리, \(\prod_{x\in\mathbb{R}^d}d\phi(x)\)는 무한 차원 공간, 즉 함수들의 모임 위에 있는 르벡 측도 (넓이 혹은 부피)가 되는 것이죠. 하지만, 무한차원공간 위에서는 르벡 측도가 존재하지 않는다는 것을 증명할 수 있기 때문에, 우리가 직면한 주요 과제는 경로적분을 기술하는 깁스 측도의 존재를 어떻게 수학적으로 보이는가에 있습니다. 이런 무한차원 깁스 측도를 어떻게 건설 ^{construction of Gibbs measures}하느냐의 문제는 구성적 양자장론 ^{Constructive quantum field theory}의 주된 목표입니다.

앞서 말한 대로, 양자장론의 목표는 양자역학 그리고 상대성 이론을 조화시키는 것이라고 했습니다. 상대성 이론은 물리 시스템이  푸앙카레 군의 작용, 즉 회전이나 이동^{rotations, translations}등에 대해 불변해야 한다는 중요한 원리를 기반으로 합니다. 따라서

구성적 양자장론^{Constructive quantum field theory}은 푸앙카레 군의 작용하에서 불변하는 깁스 측도를 수학적으로 엄밀히 건설하는 것을 목표로 합니다.

이를 정확히 표현하면 구성적 양자장론에서 말하는 양자장론의 건설은, 깁스 측도가 (1) 확률 측도이면서 (\(Z_\hbar<\infty\)) 동시에 (2) 다음의 “오스터발더-슈레이더 공리^{Osterwalder-Schrader axiom}“}를 만족하는 측도의 건설을 의미합니다:

(1) 정칙성^Regularity

(2) 유클리드 불변성^{Euclidean invariance}

(3) 반사 양성성^{Reflection positivity}

이 공리는 양자역학과 상대성 이론을 조화시키는데 필요한 최소한의 조건을 제공합니다.

하지만, 위의 세 가지 조건을 동시에 만족하는 깁스 측도를 건설하는 것은 매우 드물게 알려져 있습니다. 우리는 우선 위의 3가지 조건을 만족하면서 확률 측도가 되는 가장 단순한 모델을 살펴보고자 합니다. 논의를 간편히 하기 위해, 우리의 장 \(\phi:\mathbb{R}^d\to G\)는 스칼라 값을 (\(G=\mathbb{R}\))가진다고 가정하고, 다음의 작용 함수 \(S(\phi)\)를 고려하도록 하겠습니다.
\begin{align*}
S(\phi)=\frac 12 \int_{\mathbb{R}^d} |\bigtriangledown \phi|^2 dx.
\end{align*}

그러면, 위의 깁스 측도는 다름 아닌 공분산 ^covariance이 \((-\Delta)^{-1}\) 인  가우시안 자유장 ^{Gaussian free field}으로, 무한차원 공간 위에서의 가우시안 측도로 이해할 수 있습니다.

\begin{align*}
d\mu(\phi)=Z^{-1}e^{-\frac{1}{2} \int |\bigtriangledown \phi|^2 dx } \prod_{x\in \mathbb{R}^d}d\phi(x).
\end{align*}

확률론의 여러 곳에 등장하는 가우시안 자유장과 관련해서는 남경식 교수님의 HORIZON 기사인 “2022 리오빌 양자중력: 무작위 곡면의 성질에 관하여“를 읽어보시면 도움이 될 것으로 생각됩니다.

이러한 가우시안 자유장은 위에서 언급한 세 가지 조건 (1) 정칙성, (2) 유클리드 불변성, 그리고 (3) 반사 양성성을 모두 충족하는 것으로 알려져 있습니다.

하지만 가우시안 자유장은 서로 상호 작용하지 않는 입자들의 단순한 시스템을 설명합니다. 따라서 다음 질문은

가우시안이 아닌 입자 간의 상호작용을 기술하는 유클리드 양자장론을 구축할 수 있을까?

가 되겠습니다. 이에 답하기 위해 그다음으로 단순한 양자장론의 대상인 “\(\Phi^4\) 양자장론”을 살펴보도록 하겠습니다. 이는 기존 가우시안 자유장의 작용함수 \(\frac 12\int_{\mathbb{R}^d}|\bigtriangledown \phi|^2 dx\)에 4차 자기 상호작용 (quartic self-interaction) 포텐셜을 추가해 주는데, 여기서 포텐셜을 \(V(\phi)=\frac{1}{4}\int_{\mathbb{R}^d}\phi^4 dx\)로 정의합니다. 이를 \(\Phi^4\) 양자장론이라고 부르며, 작용 함수 \(S(\phi)\)는 커플링 상수 \(\lambda \ge 0\) 와 함께 다음과 같이 주어집니다
\begin{align*}
S(\phi)=\frac{\lambda}{4} \int_{\mathbb{R}^d} \phi^4 dx+\frac 12 \int_{\mathbb{R}^d} |\bigtriangledown \phi|^2 dx.
\end{align*}

이러한 양자장론은 보존^bosonic 이면서, 스칼라 장의 4차 자기 상호작용을 나타내는 유클리드 상대론적 양자장 이론^{Euclidean version of relativistic quantum field theory}을 의미합니다. 이전 논의에 따른다면, \(\Phi^4\) 양자장 이론을 수학적으로 건설한다는 것은 양자역학과 상대성이론을 결합하기 위한 최소한의 공리인 (1) 정칙성, (2) 유클리드 불변성, 그리고 (3) 반사 양성성을 모두 만족하는 다음의 확률 측도 (\(Z<\infty\))를 건설하는 것입니다
\begin{align}
d\Phi^4(\phi)&=\frac 1Z e^{-S(\phi)}\prod_{x}d\phi(x)=\frac 1Z e^{-\frac {\lambda}4 \int \phi^4 dx } \underbrace{e^{-\frac 12 \int | \bigtriangledown \phi|^2 dx } \prod_{x}d\phi(x)}_{\text{\(\mu\)=가우시안 자유장 }  }.
\label{Phi4} \qquad
\text{     (5.2)} 
\end{align}

하지만 \(\Phi^4\) 양자장론을 건설하는 일은 정칙성, 유클리드 불변성, 그리고 반사 양성성을 증명하는 것 외에도 확률 측도 건설부터 쉽지 않습니다. 왜냐하면 가우시안 자유장은 다음과 같은 상관 함수^{correlation function}를 가지는데
\begin{equation}
\mathbb{E}_\mu\big[\phi(x)\phi(y)\big]=G(x-y)\approx \begin{cases}
-\log|x-y| \qquad &\text{\(d=2\) 일때} \\
\frac{1}{|x-y|^{d-2}} \qquad &\text{\(d\ge 3\) 일때}
\end{cases} \qquad
\text{     (5.3)} 
\label{green}
\end{equation}

여기서 작은 규모 \(|x-y|\to 0\)^{small scale} 에서는, 즉 \(G(0)\)가 무한대로 가기 때문에, 가우시안 자유장 하에서 샘플 추출 시 그것은 함수로서 해석할 수 없게 됨을 알 수 있습니다 (각각의 장 \(\phi\)들은 \(\mathbb{R}^d\)위에 있는 점 별로 계산될 수 없습니다). 따라서 가우시안 자유장은 일반적인 함수가 아닌 일반화된 함수 ^{generalized function} 공간 위에 존재하는 확률 측도가 된다는 것을 알 수 있습니다. 함수가 아닌 장 \(\phi\)에 대해서 우리는 4제곱을 하는 \(\phi^4\)을 정의할 수 없기 때문에, 가우시안 자유장하에서 주어진 \(\phi^4\) 상호작용은 어떠한 의미도 가질 수 없음을 알 수 있습니다. 물리학에서는 이러한 문제를 극복하기 위해 무한대를 빼주는 재규격화^{renormalization} 과정을 수행하게 됩니다
\begin{align*}
S(\phi)=\frac 12\int_{\mathbb{R}^d} |\bigtriangledown \phi|^2 +\frac{\lambda}{4} \int_{\mathbb{R}^d} \phi^4 -\color{red}{\infty} \cdot \phi^2 dx.
\end{align*}

중요한 점은 알맞은 양의 무한대를 정확히 빼줘야 한다는 데 있는데, 이러한 재규격화 과정에 대해서는 다음 연재에서 더 자세히 다루도록 하겠습니다.

이 절을 마무리하기 전에 마지막으로 언급하고 싶은 것은, 1960년대에 시작된 \(\Phi^4\)-양자장론 건설 프로그램이 4차원에서 2차원 또는 3차원으로 차원이 줄어들 때 상당한 진전을 이뤘다는 것입니다. 특히, 넬슨에 의한 \(\Phi^4_2\) 이론과 글림-재피 ^Glimm-Jaffe에 의한 \(\Phi^4_3\) 이론(각각 차원이 2와 3인 경우)이 이루어졌으며, 최근에 개발된 바라슈코프-구비넬리^{Barashkov-Gubinelli}의 확률적 변분 접근법을 통한 \(\Phi^4\) 측도 건설이 수학적으로 더 엄밀한 방식으로 이해되었습니다. 그러나 4차원에서 “오스터발더-슈레이더 공리^{Osterwalder-Schrader axiom}“를 만족하는 상호 작용하는 \(\Phi^4\) 양자장론을 엄격히 건설한 사례는 없습니다. 더 정확히 말하면, 4차원 이상인 경우 자명함^triviality 즉, 가우시안 자유장과 같은 상호 작용이 없는 이론만이 건설될 수 있다는 것이 알려져 있습니다. 다시 말해, 어떤 재규격화^{renormalization} 방법을 사용하더라도, 깁스 측도는 결국 가우시안 자유장으로 수렴한다는 것입니다. 오차원 이상 (\(d \ge 5\))에서는 이미 오래전에 아이즈만^Aizenman과 프로릭^Fröhlich에 의해 자명함^triviality이 증명되었으며, 사차원에서의 문제는 오랜 기간 동안 해결되지 않았었는데, 이러한 결과는 최근에 아이즈만과 2022필즈 메달 수상자인 뒤미닐코팽^{Duminil-Copin}에 의해 사차원으로 확장되었습니다. 2022년 필즈상 수상자인 뒤미닐코팽에 대해서는 박성철 박사님의 HORIZON 기사인 “2022 필즈상 수상자 위고 뒤미닐-코팽“를 읽어보시면 도움이 될 것으로 생각됩니다.

6. 확률적 양자화: 특이 확률 편미분 방정식을 통한 양자장론의 건설

이전 절에서 우리는 구성적 양자장론^{constructive quantum field theory}에서 말하는 무한차원 깁스 측도의 건설 문제를 다루어 왔는데, 이번 절에서는 편미분 방정식을 통해 양자장론을 어떻게 건설할 수 있는지 살펴보도록 하겠습니다. 이전 절의 논의에 따르면 양자장론의 건설은 정칙성, 유클리드 불변성, 반사 양성성이라는 세 가지 조건을 만족하는 깁스 측도를 건설하는 것을 의미합니다. 그러나 이 깁스 측도가 굉장히 복잡한 장들의 모임인 무한차원 공간 위에 존재한다는 점을 미루어볼 때, 이 깁스 측도를 직접 다루는 데 어려움이 있었습니다. 이번에는 넬슨과 파리지 (2021년 노벨 물리학상 수상자), 그리고 우가 제시한 방법인 확률적 양자화^{stochastic quantization}를 통해 이 문제에 접근하고자 합니다. 도입부에서 한 번 언급했지만, 확률적 양자화를 요약하는 중요한 문장이라 생각되어, 다시 한번 다음 문장을 음미하고 넘어가 보겠습니다.

확률적 양자화란, 양자장론의 무한차원 확률 측도를 고전역학 또는 열역학의 법칙들로부터 얻어진 보다 구체적인 확률 편미분 방정식을 통해 이해할 수 있다.

앞에서 살펴본 뉴턴 운동법칙으로부터 얻어진 랑주뱅 동역학^{Langevin dynamics} (3.1)과 브라운 동역학^{Brownian dynamics} (4.1)에서 중요했던 사실은 초기조건이 어떤 확률분포인가에 상관없이 시간이 충분히 흐르면 확률 미분방정식의 해가 유한차원 깁스 측도로 수렴한다는 것이었습니다. 유한차원에서 일어나는 이러한 현상 즉, 에르고딕성^ergodicity (3.3), (4.2)이 무한차원에서도 이루어진다는 믿음을 가진다면 우리는 다음과 같은 \(\Phi^4\) 양자장론의 깁스 측도가
\begin{align*}
d\Phi^4(\phi)&=Z^{-1} e^{-S(\phi)}\prod_{x \in \mathbb{R}^d}d\phi(x)=Z^{-1} e^{-\frac {\lambda}4 \int \phi^4 -\color{red}{\infty} \cdot \phi^2 dx } \underbrace{e^{-\frac 12 \int | \bigtriangledown \phi|^2 dx } \prod_{x\in \mathbb{R}^d}d\phi(x)}_{\text{$\mu$=가우시안 자유장 }}.
\end{align*}

랑주뱅 동역학^{Langevin dynamics} (3.1)과 브라운 동역학 ^{Brownian dynamics} (4.1)의 무한차원 버전인 “특이” 확률 편미분 방정식^{singular stochastic PDE}의 균형 분포^{equilibrium distribution}로 이해될 수 있다는 것입니다

\begin{align}
\textbf{특이 확률 파동 방정식:}& \qquad  \partial _t^{2} u+\partial _t u – \Delta u + u^{3}-\color{red}{\infty} \cdot u  =  \sqrt 2\xi, \quad(6.1)
\label{wave}\\ 
\textbf{특이 확률 열 방정식:}& \qquad \partial u –  \Delta u + u^{3}-\color{red}{\infty} \cdot u  =  \sqrt 2\xi,\qquad \qquad(6.2)\\ 

Law(u(t))& \qquad \to \qquad Z^{-1}e^{-S(\phi)}\prod_{x\in \mathbb{R}^d}d\phi(x) \qquad \text{$t\to \infty$ 일 때}. \notag
\end{align}

여기서 \(\xi\)는 시간과 공간 \(\mathbb{R}_+\times\mathbb{R}^d\) 상의 가우시안 백색 소음^{space-time white noise}입니다.

따라서 \(\Phi^4\) 양자장론 건설 문제는 위와 같은 \(\Phi^4\)-동역학 모델, 즉 “특이” 확률 편미분 방정식^{singular stochastic PDE}을 공부하는 것으로 바뀔 수 있다는 것을 알 수 있습니다 (좀 더 구체적으로는 확률 미분 방정식들의 전역 해^{global solution}를 구하는 문제로 바뀌게 됩니다). 이러한 확률적 양자화의 개념은 일찍이 넬슨과 파리지 그리고 우에 의해 이미 20세기에 소개가 되었지만, 특이 확률 편미분방정식을 푸는 것은 상당히 오랜 기간 미해결 문제로 남아 있었습니다. 2010년 중반 이후에 하이러, 구비넬리 등의 선도적인 연구 이후에 발전된 여러 기법을 통해 고차원에서의 특이 확률 편미분 방정식 해를 구하는 방법들이 최근 많이 알려지게 되었는데, 이는 양자장론의 건설 문제를 편미분 방정식을 활용하여 해결할 수 있는 또 다른 접근법을 제시하게 된 것입니다. 따라서 최근 구성적 양자장론은 특이 확률 편미분 방정식과의 관련성으로 다시 큰 주목을 받고 있습니다. 위의 논의에서는 장들이 스칼라 값을 갖는 경우에만 초점을 맞췄지만, 스칼라 장이론뿐만 아니라 게이지 그룹 \(G\)가 컴팩트 리 그룹^{compact Lie group}일 때의 양자장론 (양-밀스 이론과 같은)에서 역시 확률적 양자화를 사용하는 것이 가능합니다. 따라서 많은 게이지 이론^{gauge theory}에 등장하는 깁스 측도 건설 문제 또한 편미분 방정식을 이용해 해결해 나가고 있습니다.

7. 글을 마치며

하이러와 구비넬리의 기법으로 파리지-우의 확률적 양자화의 아이디어가 수학적으로 실현이 된 후에 양자장론과 편미분 방정식, 확률론은 서로 뗄 수 없는 관계가 되었습니다. 제가 연구해 오고 있는 무한차원 깁스 측도들의 건설 문제, 온도 혹은 열역학적 극한에 따른 깁스 측도의 집중 혹은 붕괴 현상들은 확률 열 방정식, 확률 파동 방정식의 분석을 통해 이루어집니다. 반대로 편미분 방정식 장시간^{long time}의 여러 통계적 성질 (에르고딕성과 같은)을 이해하기 위해서도 양자장론의 깁스 측도를 사용해 오고 있습니다. 이처럼 서로 상관없어 보였던 수학과 물리학의 여러 세부 분야가 연결되는 과정을 느끼는 것은 큰 즐거움이 아닐 수 없습니다. 달라 보이는 여러 수학, 물리학의 연결점을 찾아내는 즐거움이 독자분들께도 전달되었기를 바라며 이번 편을 마치고자 합니다.

이후 연재에서는 이번 편에서 다루지 못한 무한대를 빼주는 재규격화^{renormalization}, 섭동 이론^{perturbation theory}과 파인만 다이어그램^{Feynman diagram}, 그리고 확률적 양자화를 통해 얻은 특이 확률 편미분 방정식을 어떻게 풀 수 있는가에 대해서 살펴보도록 하겠습니다.