2024 아벨상 수상자 미셸 탈라그랑

    2024년 아벨상 수상자로 프랑스 National Centre for Scientific Research ^CNRS 의 미셸 탈라그랑 ^{Michel Talagrand}이 선정되었습니다. 아벨상 위원회는 다음을 근거로 수상자를 선정하였습니다: “확률론과 함수해석학 발전에의 획기적인 기여, 그리고 수리물리학과 통계학으로의 응용”. 필자는 확률론을 연구하면서 Talagrand의 이론을 수도 없이 자주 마주하였습니다. Talagrand 논문들의 신기한 점은, 수많은 논문들이 공동 연구가 아닌 Talagrand의 독자적인 연구로 진행되었다는 점입니다. 필자는 논문들을 읽으면서 이러한 아름다운 이론을 어떻게 혼자 힘으로 다 발전시켰는지 궁금증과 경외심이 늘 들었습니다. 이번에 Talagrand가 아벨상을 수상했다는 소식을 듣고 매우 기뻤음과 동시에 받을 만한 분이 선정되었다는 생각이 들었습니다.

    아벨상 위원회에 따르면, 구체적으로 Talagrand는 다음 세 가지 분야를 발전시킨 공로로 아벨상을 수여하였습니다.
     1. 확률과정의 최대값
     2. 집중 현상
     3. 스핀 유리 ^{spin glass}
스핀 유리에 관한 업적을 이해하기 위해서는 많은 수학적 설명이 필요하여 이 글에서는 1번과 2번에 대해 이야기해보도록 하겠습니다.

    확률과정의 최대값

    확률과정이란, 시간에 따라 무작위하게 변화하는 대상입니다. 확률과정의 최대값을 구하는 것은 자연스럽고 중요한 질문입니다. 예를 들어, 해안가를 강타하는 무작위하게 움직이는 파도의 가장 높은 파고를 구할 수 있다면, 우리는 방파제를 효율적으로 쌓아올려서 자연재해를 잘 대비할 수 있을 것입니다. 하지만 이러한 확률과정의 최대값을 구하는 것은 매우 어려운 문제이며, 일반적인 공식이나 방법론이 존재하지 않습니다.

    일반적으로, 최대값을 구할 수 있는 가장 단순한 방법은 합집합 방법 ^{union bound}입니다.

\begin{align}\label{1}
\mathbb{P} \big(\sup_{t=1,2,\cdots,N} X_t > K\big) = \mathbb{P} ({X_1,\cdots,X_N 중 적어도 하나가 K 보다 크다}) \le \sum_{t=1}^N \mathbb{P} (X_t>K).      (1)
\end{align}     이 방법이 간단한 이유는, 전체 확률과정의 분포 ^{joint distribution} 가 무엇이든 간에, 각 시점 \(t \)에서의 확률분포 \(X_t\)만의 정보 ^{marginal distribution} 만으로 최대값의 상한을 구할 수 있기 때문입이다. 하지만 이 방법은 매우 큰 약점을 가지고 있는데, 확률변수의 개수 \(N\)이 크다면 우변의 항이 많아지기 때문에 올바르지 않은 상한을 제공합니다. 특히, 매개변수가 연속인 경우 ^{예시: 시간의 흐름}, \(N\)이 무한대가 되어 쓸모가 없어집니다.

    이 문제를 극복하기 위해, 변수 개수를 줄여봅시다. 만약 다음 그림 1처럼 같은 분할 ^{같은 색깔} 내에서 확률변수들이 “비슷”한 값을 가진다면, 다음과 같이 쓸 수 있습니다.
\begin{align}\label{2}
\mathbb{P} \big(\sup_{t\in T} X_t > K\big) \approx \mathbb{P} (\sup_{t=1,2,\cdots,m} X_t > K) \le \sum_{t=1}^m\mathbb{P} (X_t>K).     (2) \end{align} 
즉, 변수 개수를 크게 줄일 수 있어서, 위의 합집합 방법이 유용하게 작용할 수 있습니다.

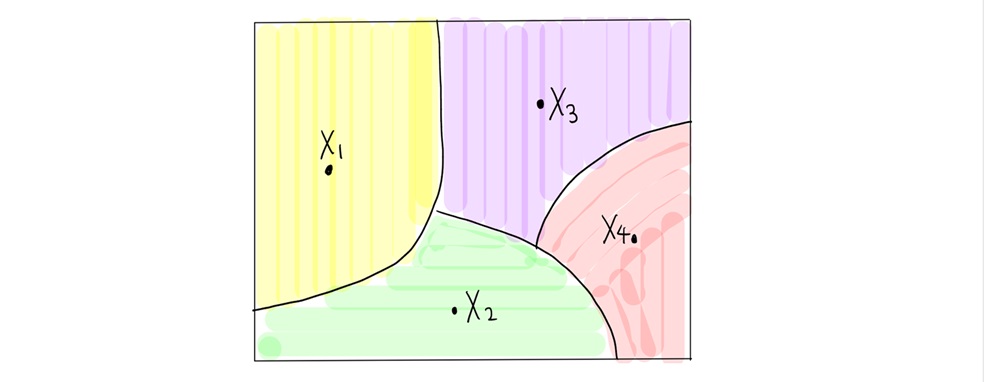
    그렇다면 확률변수들이 “비슷”하다는 말이 정확히 무엇일까요? 확률과정 \(\{X_t\}_{t \in T}\)이 특별히 “가우시안” 분포를 따른다면, 자연스러운 거리를 부여할 수 있습니다.

\begin{align*} d(s,t) := \mathbb{E} [|X_s-X_t|^2]. \end{align*}

직관적으로 다음과 같이 이해할 수 있습니다.

즉, 확률변수들이 “비슷”하다는 말은 강한 상관관계가 있으며, 거리가 가깝다는 뜻입니다. 특히 “가우시안” 분포인 경우에는 거리들의 정보가 확률과정의 전체 분포를 결정짓습니다.

    위의 식 (2)에서 오차를 줄이기 위해 분할을 정밀하게 택하게 된다면 분할 개수 \(m\)이 많아져서 상한이 너무 커지게 되고, 반대로 분할 개수를 줄인다면 오차가 커지게 됩니다. 이 둘의 상반된 효과를 극복하기 위해 위 그림 1과 같은 하나의 분할이 아니라, 계급 구조^hierarchy 를 갖는 “무한 다단계 분할”에 정교하게 적용하면 상한을 더 정확하게 구할 수 있습니다. 다음 그림 2.처럼 단계가 올라갈수록 분할이 점점 더 섬세해질 때, \((A_n)_{n}\)을 “무한 다단계 분할”이라고 합니다.

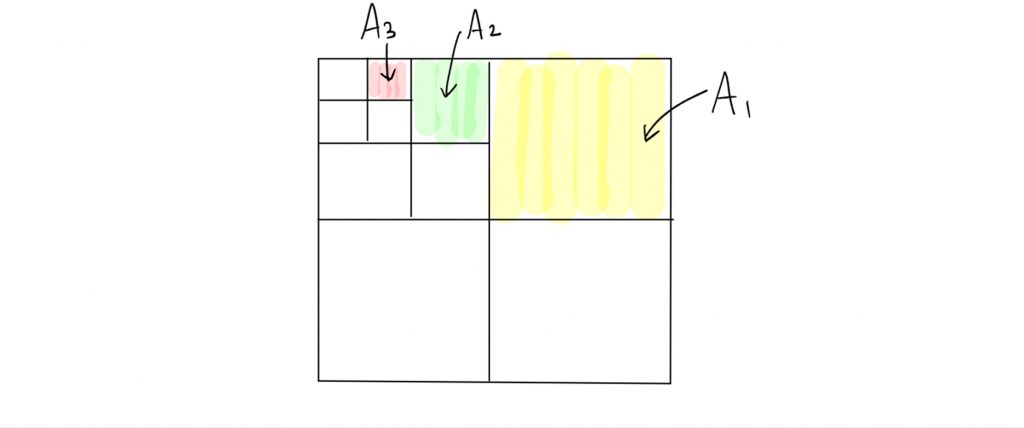
Talagrand는 이렇게 정교하게 구한 상한이 본질적으로 최대값의 하한과 일치한다는 사실을 증명하였습니다 [3]: \(T\)의 분할 \(A_n\)에 대하여, \(t\in T\)를 포함하는 부분을 \(A_n(t)\)라고 할 때,

\begin{align*} \mathbb{E} \big[\sup_{t\in T} X_t\big] \asymp \inf_{\substack{{무한 다단계 분할 } (A_n)_{n \ge 0} \\ |A_n| \le 2^{2^n}}} \ \Big[ \sup_{t\in T} \ \sum_{n=0}^\infty 2^{n/2}\cdot \text{diam}(A_n(t))\Big]. \end{align*}

즉, Talagrand는 가우시안 확률과정의 최대값을 거리 공간의 기하학적 성질에만 의존하는 값으로 근사하는 데에 성공하였습니다. 참고로, 위 식에서 \(|A_n| \le 2^{2^n}\) 조건은 \(|A_{n+1}| \le |A_{n}|^2\) (다음 레벨 분할의 상한)에서 귀납적으로 나온 것입니다.

    이 Talagrand의 결과는 수많은 분야에 응용될 수 있습니다. 두 예시를 간략히 소개하겠습니다.

    – 응용 1 (덮는 시간). 다음 질문을 생각해봅시다. “무작위로 국내 배낭여행을 떠나봅시다. 하루마다, 각 도시에서 인접한 도시를 무작위로 골라 관광합시다. 물론, 같은 도시를 두 번 이상 방문할 수 있습니다. 이 때, 모든 도시를 방문하는 데에 며칠 걸릴까요?”

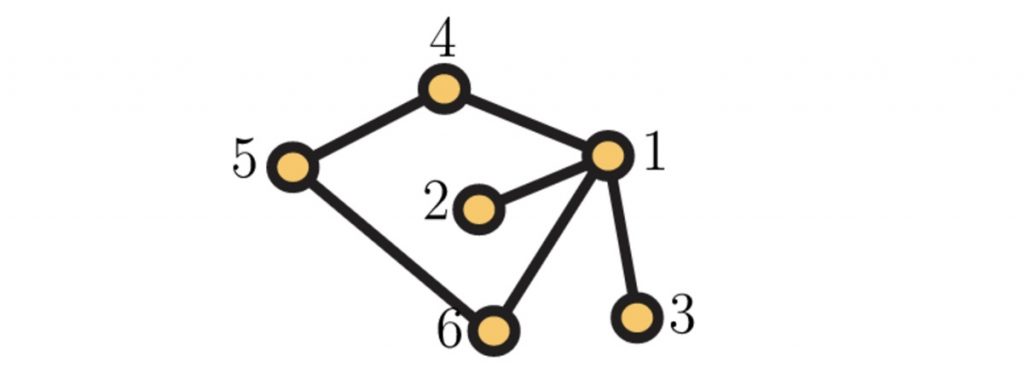
    이 개념을 확률론에서는 덮는 시간^{cover time} 이라고 부릅니다. 놀랍게도, 일반적인 연결그래프 \(G = (V,E)\)에서 움직이는 무작위 걸음이 전체를 덮는 시간은, 그래프 위에서 정의된 특정한 가우시안 확률과정^{Gaussian free field} 의 최대값의 제곱과 본질적으로 같다는 사실이 알려져 있습니다 [1]:

\begin{align*} {덮는 시간의 기대값} \asymp |E| \cdot \Big(\mathbb{E} [\sup_{v\in V} X_v]\Big)^2.\end{align*}

    – 응용 2 (차원 감소). 우리가 고차원의 공간을 생각할 때, 이를 단순화하기 위해서 차원을 줄이는 방법을 자주 생각합니다. 이 관점은 수학 뿐만 아니라, 통계학과 머신러닝^{주성분 분석}, 공학^{압축 센싱} 등 다양한 분야에서 사용됩니다. 거리 기하학^{metric geometry}에서는 이를 차원 감소^{dimension reduction} 문제라고 부르며, 립쉬츠 매장 ^{bi-Lipschitz embedding} 문제와도 깊은 관련이 있습니다. 차원 감소와 관련된 다음과 같은 사실이 있습니다 [2].

    [정리] 반지름이 1인 \(N\)차원 구의 부분집합 \(X\)를 생각하자. 이 때, 다음 조건을 만족하는 차원 \(M\)과 선형함수 \(\Phi:\mathbb{R}^N \rightarrow \mathbb{R}^M\)가 존재한다.

• \(M = O(\big[\mathbb{E} \sup_{x\in X} |\langle x, G\rangle | \big]^2)\) (\(G\)는 \(N\)차원 가우시안 정규분포).
• 모든 \(x\in X\)에 대해, \(||\Phi x|| \approx 1\). 

첫 번째 조건에서 \( a= O(b)\)라는 표현은, \(a\)가 최대한 \(b\)의 선형함수만큼 커진다는 뜻입니다. 이 정리는 기존의 기하학적 구조를 크게 변화시키지 않으면서 차원을 줄일 수 있다고 말합니다. 흥미로운 점은, 줄어든 차원 \(M\)이 기존에 주어진 차원 \(N\)에 의존하지 않는다는 것입니다. 즉, 기존 차원이 아무리 높더라도, 줄어든 차원은 주어진 집합과 연관된 가우시안 확률과정의 최대값에만 의존한다는 것입니다.

    집중 현상

    우리는 고도 정보화의 시대에 수없이 많은 개수의 데이터를 접하면서 살고 있습니다. 데이터의 개수가 매우 많다면, 평균 회귀 현상이 발생합니다. 가장 간단한 예시로, 동전을 1000번 던진다면, 큰 수의 법칙에 의해서 앞면은 근사적으로 500번 나올 것입니다. 집중 현상^{concentration phenomenon} 이란, 매우 높은 차원에서 정의된 함수가 그 평균에 얼마나 집중되어 있는지를 “정량적으로” 나타내는 용어입니다. Talagrand는 볼록성을 반영하는 새로운 거리 개념을 도입하여, 집중 현상을 규명하였습니다 [4]. 그 중 가장 특수한 경우를 소개하겠습니다.

    [정리] 무작위로 (균등한 확률로) 뽑은 \(N\)차원 벡터 \(\{-1,+1\}^N\)를 \(X\)라고 부르자. 차원 \(N\)에 의존하지 않는 적당한 상수 \(c>0\)가 존재하여 다음 부등식이 성립한다. \(N\)차원 공간 \(\mathbb{R}\)^N의 임의의 볼록집합 \(A\)에 대해, \(A_t:= \{x\in \mathbb{R}\)^N: d(x,A)\le t\}\) (\(t>0\))라고 할 때,

                          \(\mathbb{P}(X\in A) \cdot \mathbb{P}(X\notin A_t) \le e^{-ct^2}\).

즉, 볼록집합 \(A\)가 \(2^N\)개의 벡터 \(\{-1,+1\}^N\)들 중 적당 비율을 포함한다면, \(t \gg 1\)에 대해 \(A_t\)는 거의 모든 벡터를 포함한다는 것을 의미합니다. 여기서 핵심적인 부분은 부등식이 차원 N에 의존하지 않는다는 점입니다. 이는 본질적으로 \(A\)의 볼록성 때문에 성립하며, 볼록 성질이 빠진다면 위 사실은 성립하지 않습니다. 이 부등식이 유용한 이유는, 수많은 데이터들이 주어져도 거리함수와 같은 볼록성을 띄는 확률변수는 데이터의 수와 무관하게 집중 현상이 나타나기 때문입니다. 특히, 차원이 무한대로 커져도 집중 현상이 균질하게 나타나기 때문에, 무한차원 공간의 분석 등 함수해석학 연구에 유용한 도구로 사용되기도 합니다.

    맺음말

    Talagrand는 확률론의 다양한 문제들을 색다른 시각으로 바라보아 아름답고 새로운 이론을 만들어내었습니다. 이 이론은 확률론 뿐만 아니라 함수해석학, 거리 기하학, 수리물리학, 통계학 등 수많은 다른 분야에도 적용되고 있습니다. 이 뿐만 아니라, Talagrand는 수리물리학의 중요한 난제도 해결하였습니다. 그 중요한 예시 중 하나로, 2021년에 노벨 물리학상을 수상한 물리학자 Giorgio Parisi가 추측한 통계물리학의 스핀 유리^{spin glass} 모델의 자유 에너지^{free energy}에 관한 오랜 난제를 해결한 것을 꼽을 수 있습니다 [5]. 이는 Talagrand의 아벨상 수여의 세 번째 주요 업적으로 인정받았습니다.