나눗셈과 준군의 호모토피 기수

    어릴 적, 우리는 사탕 몇 개를 눈앞에서 이리저리 움직여 가며 덧셈을 배웠다. 사탕이 오른손에 두 개, 왼손에 세 개가 있으면 사탕은 모두 다섯 개, 이런 식으로. 이는 덧셈을 직관적으로 표현하는 좋은 방법이다. 조금 정제된 단어들로 말하자면, 덧셈의 메커니즘은 `집합의 합집합’으로 이해할 수 있다는 것이다. 이러한 관점을 발전시키면, 숫자의 곱셈은 `곱집합’을 통해 이해할 수 있다. 그렇다면 이 관점을 발전시켜 나눗셈을 표현할 수 있을까?
    범주론은, 역사적으로는, 대수 위상에서 나타나는 현상을 정립하기 위한 언어로 등장했다. 하지만 이 언어는 많은 수학자들을 거쳐오며 현대 수학과 물리의 핵심적인 원리를 제공해오고 있다. 이 글을 통해 범주 중에서 비교적 이해하기 쉬운 준군을 소개하고, 위와 같은 관점에서 나눗셈은 준군을 유도하는 것을 설명한다. 특히, 준군의 불변량인 호모토피 기수로부터 나눗셈이 복원되는 것을 살펴본다.

1. 대진표와 작용의 궤도

HORIZON에 글을 실어달라는 제안을 받았던 1월 말, 아시아의 축구 축제인 아시안 컵이 열리고 있었다. 밤늦게 시청하던 기억이 아직도 새록새록하다. 이런 큰 대회에서 사람들의 이목을 끄는 것 중 하나는 바로 대진표이다. 대진표는 경기가 예정된 나라끼리 짝을 짓는 것을 도식화한 도구다. 간단한 예시로 8강전을 생각해보자. 올해는 호주, 한국, 타지키스탄, 요르단, 카타르, 우즈베키스탄, 이란 그리고 일본, 총 8개의 나라들이 올라왔다. 여기에서 초등적인 질문을 던져본다. 8강전에서 우리가 보게 되는 경기는 총 몇 경기일까? 아이들이 나눗셈을 처음 배울 때 손으로 직접 움직이며 배우는, 일종의 `짝을 짓는’ 문제이다. 물론, 8강전에서 4번의 경기를 볼 수 있다. 왜냐하면 두 팀씩 묶다보면 네 번의 묶음에서 완료되기 때문이다.

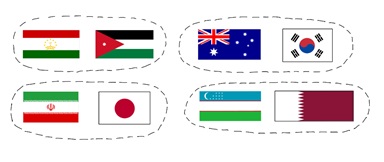
    이 관찰은 초등적이지만, 다시 음미해보자. 간단하게 위의 8개의 나라들이 이루는 집합을 \(\mathbf{C}\)^countries 라고 두자. 개념에 대한 설명은 잠시 뒤로 미루고, 앞선 관찰을 재해석해보면 다음과 같다.

1.  두 나라끼리 짝을 짓는 것은, 군 \(\mathbf{Z}_2\)가 집합 \(\mathbf{C}\)위로 작용한다는 것과 상응한다.
2.  대진표는 그 작용의 궤도가 이루는 집합과 같다.

    이번 단원의 목표는 위에 쓰여진 언어를 이해해보는 것이다. 우선, 군^group 이란 결합법칙을 만족하는 이항연산\(~\cdot~\) 이 주어진 집합이다. 군은 그 연산에 대하여 항등원을 갖고, 모든 원소들이 역원을 갖는다. 군론에 대한 훌륭한 교과서가 많으니 여기에서 추상적인 것을 다루는 것은 피하고, 구체적인 군 \(\mathbf{Z}_2\)를 살펴보고 싶다. 군 \(\mathbf{Z}_2\)은 \(1\)과 \((-1)\)이라는 두 개의 원소를 갖고 있다. 이 군의 이항연산 \(\cdot\)을 (표 1)에서 설명한다. 예를 들어 연산 \((-1)\cdot (-1)\)은 \(1\)을 내놓는다. 또한 \(1\)이 항등원의 역할을 하고 있음을 알 수 있다.

정의 1.1. 군 \(G\)가 집합 \(X\)에 작용한다는 것은, 군 \(G\)의 원소 \(g\)마다 집합 \(X\) 위의 함수 \(f_g : X \to X\)가 주어져서 다음을 만족하는 것을 말한다.

1.  \(e\)를 군 \(G\)의 항등원이라고 할 때, 함수 \(f_e\)는 \(X\) 위의 항등함수와 같다. 즉, \(f_e (x) =x\)이다.
2.  군 \(G\)의 원소 \(g,h\)에 대하여 합성 \(f_g \circ f_h\)은 \(f_{g \cdot h}\)와 같다. 즉, \(f_g ( f_h (x )) = f_{g \cdot h} (x)\)이다.

       다시 말해서 군의 작용은 군의 구조를 집합 \(X\) 위의 함수로 표현하는 체계라고 생각할 수 있다.

정의 1.2. 군 \(G\)가 작용하는 집합 \(X\)를 생각하자. 어떠한 \(x \in X\)가 군의 작용을 통해 `이동 가능한 궤적’을 다 모은 것을 궤도^orbit라고 부른다. 정확히는, 임의의 \(g \in G\)에 대해 \(f_g(x)\)들을 모아서 만들어지는 \(X\)의 부분집합이다. 

정의 1.3. 모든 궤도들이 이루는 집합을 \(X/G\)라고 쓴다¹.

    새로운 언어를 얻었으니 8강전의 예시로 돌아가보자. 이번에는 대진표로부터 집합 \(\mathbf{C}\) 위의 \(\mathbf{Z}_2\)의 작용을 만들 것이다. 작용의 정의상, \(\mathbf{C}\) 위의 두 함수 \(f_1,f_{-1}\)을 구성하면 된다. \(1 \in \mathbf{Z}_2\)은 항등원이므로 \(f_1\)은 항등사상으로 두면 충분하다. 그리고 나라 \(x\)에 대하여 \(f_{-1}(x)\)는 `\(x\)와 대결을 펼칠 나라’로 정의한다. 그러면 `\(x\)와 대결을 펼칠 나라와 대결할 나라’는 \(x\) 자기 자신이므로, \(f_{-1}(f_{-1}(x)) = x\)도 알 수 있고, 이렇게 잘 정의된 작용이 얻어진다. 이 작용을 (그림 2)에 나타내고 있다. 각 화살표의 방향은, 어떤 나라에 \(f_1,f_{-1}\)을 작용시켰을 때 대응되는 나라를 향한다.

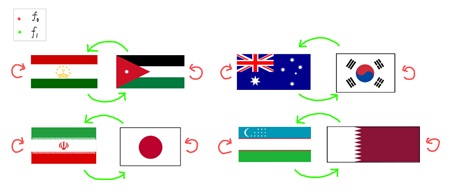
    그렇다면 이 작용의 궤도란 무엇일까? 예를 들어, `대한민국’을 포함하는 궤도는 를 `대한민국’에 작용시켜서 얻어지는 나라들로 구성되는 \(\mathbf{C}\)의 부분집합인데, 이는 결국 `대한민국’과 `호주’로 구성된다. 이로부터 이 작용의 궤도는, 대진표 상에서 같이 경기를 펼칠 팀끼리 이루는 집합과 같은 것을 알 수 있다. 따라서 (그림 1)은 이 작용에 대한 궤도들의 집합 \(\mathbf{C}/\mathbf{Z}_2\)으로 간주할 수 있다.

                                                        \(\mathbf{C}/\mathbf{Z}_2 \approx\) 나눗셈의 몫

이 관찰로부터 다음과 같은 멋진 공식을 주장하고 싶어진다. 여기서 \(|X|\)는 집합 \(X\)의 원소 개수를 나타낸다.

2. 나누어 떨어지는 것과 자유로운 작용

이 단원에서 (잘못된 정리1.4)이 참이 될 충분조건을 생각해보자. 그러기 위하여 다음 개념을 도입한다.

정의 2.1.   군 \(G\)의 작용을 받는 집합 \(X\)가 주어졌다고 하자. 그 작용이 자유롭다는 것은 임의의 \(x \in X\)에 대하여 \(f_g (x) = x\)를 만족하는 \(g\in G\)는 항등원밖에 없다는 것을 의미한다.

   다시 말해, \(x\)에 자명하지 않은 군의 원소를 작용시켰을 때 \(x\)와 반드시 다른 원소가 대응되는 것을 말한다. 예들 들어, 대진표에서 얻어졌던 군의 작용, (그림 2)와 같은 상황을 말한다.

   자유로운 군의 작용일 경우, 각 궤도의 원소 개수는 군의 원소 개수와 같다는 것을 정의로부터 알 수 있다. 예를 들어 (그림  2)를 떠올려보면, 각 궤도를 구성하는 나라의 수는 군 \(\mathbf{Z}_2\)의 원소 개수 2와 같다. \(X\)는 모든 궤도들의 합집합인 것에 주목하면, \(|X|\)는 \(|G|\)로 나누어 떨어지고 그 몫이 궤도의 수 \(|X/G|\)와 같다는 것을 알 수 있다. 즉, (잘못된 정리1.4)은 자유로운 작용에 한해서 진짜 정리로 받아들일 수 있다.

3.  나눗셈과 준군

이번에는 자유롭지 않을 수도 있는 작용에 대해 생각해보자. 군 \(G\)의 작용이 주어진 집합 \(X\)를 생각할 때, 다음과 같은 그림을 머릿속에 떠올리면 도움이 된다. 종이 한장을 꺼내서 집합 \(X\)의 원소 개수만큼의 점들을 찍는다. 그리고 각 점을 \(X\)의 원소들로 (중복 없이) 라벨을 붙여준다. 그 다음으로, 원소 \(g \in G\)와 \(x \in X\) 대하여, 점 \(X\)에서 점 \(f_g(x)\)으로 향하는 `방향을 갖는 변’을 그어주고, 그 변에는 \((x,g)\)라는 라벨을 붙여준다. 최종적으로 (그림 3)과 같이 화살표와 점들로 구성된 그림이 종이에 펼쳐져 있을 것이다.

    특징적인 변 중 하나는 \((x,e)\)일 것이다. 여기서 \(e\)는 군 \(G\)의 항등원이다. 작용의 정의에 의해 \(f_e(x) = x\)이므로, \((x,e)\)라는 라벨이 붙어있는 `방향을 갖는 변’의 양쪽 끝점은 모두 \(x\)다. 다시 말해, (그림 4)처럼 루프^loop를 이룬다.
    위의 규칙으로 그린 그림은 범주^category라고 불리는 재미있는 대수적 구조를 갖는다. 다음의 정의를 보자. 

정의 3.1. `꼭지점’들과 `방향을 갖는 변’으로 구성된 그림을 유향 그래프^{directed graph}라고 부른다. 유향그래프의 범주 구조란 다음의 정보로 구성된다.

1.  꼭지점 \(X,Y,Z\)를 생각한다. \(X\)에서 \(Y\)로의 변 \(f\)와 \(Y\)에서 \(Z\)로의 변 \(g\)가 주어지면, \(X\)에서 \(Z\)로의 변 \(g \circ f\)가 정의된다. 변 \(g \circ f\)를 \(g,f\)의 `합성’이라고 부르고, ‘합성’은 결합 법칙 \(f\circ (g \circ h) = (f \circ g ) \circ h\)을 만족한다. 
2.  `합성’에 대한 `항등사상’이 정의된다. 즉, 임의의 꼭지점 \(X\)에 대하여, 양쪽 끝점이 \(X\)자신인 변 \(1_X\)가 정의되어, \(X\)에서 \(Y\)로의 임의의 변 \(f\)에 대하여 \(f \circ 1_X = f = 1_Y \circ f\)가 성립한다. 

    앞에서 군 \(G\)의 작용을 받는 집합 \(X\)로부터 그린 그림은 유향그래프이며, 자연스러운 범주 구조를 갖는다. (그림 5)에서 파란색으로 나타낸 두 변의 `합성’을 보라색의 변으로 나타내고 있다. 이렇게 정의된 `합성’에 대해서 (그림 4)의 루프는 `항등사상’의 역할을 한다.

정의 3.2. 군 \(G\)의 작용이 주어진 집합 \(X\)에 대하여, 앞에서 구성한 범주를 \(X//G\) 로 적는다 ².

    1단원의 대진표 예시에 적용시켜보자. 8개의 나라들의 집합 \(\mathbf{C}\)의 원소들을 편의상 (그림 1)에서의 순서대로 \(A,B,C,D,E,F,H,I\)로 부르기로 하자. 그러면 우리가 앞서 살펴본 \(\mathbf{Z}_2\)의 작용을 받는 \(\mathbf{C}\)로부터 범주 \(\mathbf{C} // \mathbf{Z}_2\)가 얻어진다. (그림 6)의 이 범주를 나타내고 있다. 붉은 변들이 `항등 사상’의 역할을 한다.
    범주 \(\mathbf{C} // \mathbf{Z}_2\)를 세밀히 관찰해보면, 임의의 변들이 `합성’에 대해 역원을 갖는다는 것을 알 수 있다. 예를 들어, \(A\)에서 \(B\)로 가는 변 \((A,-1)\)의 역원이란, \((A,-1)\)과 합성해서 `항등 사상’ (항등원 루프)가 나오는 또 다른 변을 가리킨다. 여기서

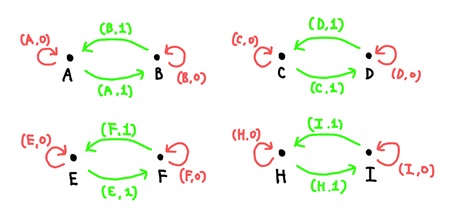
\((B,-1)\)가 \((A,-1)\)의 역원인 것을 확인해보자. (그림 5)의 규칙으로 합성 \((B,-1) \circ (A,-1)\)을 (표 1)에 따라 계산하면 \((A, (-1) \cdot (-1)) = (A, 1)\)임 알 수 있다. 비슷하게, \((A,-1) \circ (B,-1) = (B,1)\)이다. 일반적으로 군 \(G\)가 작용하는 집합 \(X\)에 대하여, 범주 \(X //G\)도 임의의 변들이 `합성’에 대해 역원을 갖는다. 이러한 성질을 다음의 개념으로 정의한다.

정의 3.3. 범주 \(\mathcal{C}\)가 준군^groupoid이라는 것은, \(\mathcal{C}\)의 모든 변들이 `합성’에 대해서 역원을 갖는 것을 말한다.

명제 3.4. 군 \(G\)가 작용하는 집합 \(X\)에 대하여, 범주 \(X //G\)는 준군이다.

     집합의 원소 개수는 집합의 `크기’를 말해준다. 두 집합 사이에 일대일 대응이 존재하면 그 `크기’는 같다는 점에서 `원소 개수’는 집합의 불변량을 제공한다. 이와 유사한 준군의 불변량을 소개한다 ³.

정의 3.5. 유한 준군 \(\mathcal{G}\)에 대하여 호모토피 기수^{homotopy cardinality} \(|\mathcal{G}|\)⁴는 다음의 규칙⁵를 통해 정의된다.

1.  \(\mathcal{G}\)가 연결 그래프일 때 다음과 같이 계산된다.  \(\mathcal{G}\)의 꼭지점 \(x\)하나를 선택한다. \(x\)를 양쪽 끝점으로 하는 변의 개수를 \(N_x\)라고 하자. 그때 호모토피 기수 는 \(N_x\)의 역수다 ⁶.
2.  \(\mathcal{G}\)의 연결 성분이 \(\mathcal{G}_1, \mathcal{G}_2, \cdots , \mathcal{G}_k\)라면, \(|\mathcal{G}| {:=} |\mathcal{G}_1| + |\mathcal{G}_2| + \cdots | \mathcal{G}_k|\)로 계산된다.

    예시를 계산하면서 익숙해져보자.

예시 3.6. (그림 6)의 준군 \(\mathbf{C}//\mathbf{Z}_2\)의 호모토피 기수를 계산해보자. 이것은 \(4\)개의 연결 성분으로 이루어져 있으므로, 정의 3.5의 두 번째 규칙에 의하여 각 성분별로 호모토피 기수를 계산하면 된다. 그 성분 중 하나로 A와 B가 포함된 성분을 생각해보자. 첫 번째 규칙을 적용시키기 위해 꼭지점 A를 선택하면, A를 양 끝점으로 하는 변은 붉은색 \((A,1)\) 하나이므로 \(N_A =1\)임을 알 수 있다 ⁷.따라서 각 성분별 호모토피 기수는 \(1\)이고,\(|\mathbf{C}//\mathbf{Z}_2|=1+1+1+1=4\)이다.

예시 3.7.  다른 중요한 예시를 하나 더 살펴보자. 이번에는 원소 \(a\) 하나만 갖는 집합 \(\{a\}\)를 생각한다. 그렇다면 집합 \(\{a\}\) 위의 \(\mathbf{Z}_2\)의 작용은 유일하게 결정날 것이다. 왜냐하면 \(\mathbf{Z}_2\)의 원소를 작용시켜 만들 수 있는 후보가 원소 \(a\) 하나밖에 없기 때문이다. 이 군의 작용에 의해 얻어지는 준군을 그려보면 (그림  7)과 같을 것이다. 따라서 \(N_a = 2\)이므로 \(|\{a\} // \mathbf{Z}_2| = 1/2\)이다 ⁸.

    준군의 호모토피 기수 덕분에 (잘못된 정리1.4)는 다음과 같이 거듭나게 된다.

정리 3.8. 유한 집합 \(X\)와 그 위의 유한군 \(G\)의 작용이 주어졌을 때, 다음의 공식이 성립한다. 

                                                     \(|X//G| = |X| / |G|\) .

4. 약분과 준군의 동치

마지막으로 소개하고 싶은 나눗셈과 준군의 유사성이 있다. 일반적인 준군 이론에서 두 준군이 `같다’라는 것을 정의하는 방법으로 준군의 동치 ^equivalence라는 관계가 있다. 이를 정확히 설명하려면 함자 ^functor 등을 설명해야 함으로 여기서 생략하지만, 준군의 동치는 그래프로써의 일치보다 훨씬 성립하기 쉬운 관계라는 것만 말해두고 싶다. 꼭지점의 개수와 변의 개수가 다르더라도 준군으로써 동치 관계에 있을 수 있다는 것이다. 예를 들어, (그림 8)의 두 준군은 그래프로써는 다르지만 준군으로써 동치의 관계에 있다.
    준군의 동치는 분수의 약분과 꽤나 비슷하다. 분자, 분모가 각각 다르더라도, 약분을 통해 서로 같은 결과를 줄 수 있다는 점이 그렇다. 이 유사성을 설명하기 위해, 간단한 예시로 \(2/2\)과 \(1/1\)를 생각하자. 1단원에서 본 것처럼 각 경우에 대해 어떤 군의 작용을 받는 집합을 생각할 수 있다. 전자일 경우, \(\mathbf{Z}_2\)가 자유롭게 작용하는 원소 두 개의 집합을 생각하고, 후자일 경우 자명한 군이 작용하는 원소 한 개의 집합을 생각한다. 이 둘은 명백히 다르게 보이지만, 각 작용이 유도하는 준군은

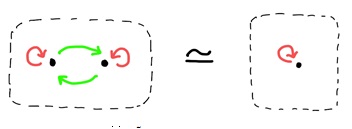
동치 관계에 있다. 이를 (그림 8)에서 나타내고 있다. 한편, 약분에 의해 \(2/2\)과 \(1/1\)은 서로 같다.
    위에서 살펴본 유사성과 (정리 3.8)에 의해, 호모토피 기수와 준군의 동치의 관계에 대해 궁금할 것이다. 이에 관해 다음의 성질을 소개한다.

정리 4.1. 호모토피 기수는 준군의 동치에 대해 불변량이다. 즉, 동치인 두 준군 \(\mathcal{G}_1,\mathcal{G}_2\)에 대하여 \(|\mathcal{G}_1| = |\mathcal{G}_2|\)가 성립한다.

5. 글을 마치며

지금까지 나눗셈 그리고 군의 작용을 통해 준군이라는 대상을 자연스럽게 받아들이는 과정을 이야기했다. 준군과 범주의 정의는 조합적이고 추상적인 형태를 취하고 있어서 다소 특수해 보인다. 하지만 수학을 공부한다면 자신도 모르게 어떤 범주의 `꼭지점’을 다루고 있을 만큼, 범주는 보편적인 개념이라고 생각한다. 그런 의미에서 참고문헌 [3]을 통해 더 다양한 이야기를 접해보길 추천한다.
    마지막으로 이 글의 주인공인 호모토피 기수와 위상수학이 맞닿는 부분이 있어서 간략히 소개하고 싶다. 유한 군 \(H\)를 하나 고정하면, 위상공간마다 준군을 자연스럽게 배정할 수 있다. 그건 위상공간 위의 \(H\)를 구조군으로 하는 주다발 ^{principal bundle} 들이 이루는 준군이다. 더 나아가 이 준군의 호모토피 기수를 대응시키면, 유리수에 값을 갖는 위상공간의 호모토피 불변량이 얻어진다. 이 불변량을 3차원 다양체에 제한시키면 Dijgkraaf-Witten 모델이라고 불리는 위상 양자장 이론으로 확장된다. 다시 말해, 이 불변량은 다양체를 잘라서 계산할 수 있는 어떤 시스템의 일부이며, 자른 단면에 대해서 (확장된) 불변량들이 고차 범주론적인 값으로 주어진다. Dijgkraaf-Witten 모델은 물리수학 혹은 수리물리와 관련이 깊을 뿐만 아니라, 저차원 위상수학과 대수의 사이를 이어준다. 이와 관련해서 [1] 혹은 그 속의 참고문헌들을 보기를 추천하며 글을 마무리한다.