중점그래프란 무엇인가?

어떤 도시에 A, B, C가 살고 있는데 서로 손해보려는 짓을 하지 않는다. 덕분에 A, B, C는 친한 다른 지인 없이 셋이서만 논다. 어느 날 이 세 명은 각자의 집에서 출발하여 적당한 위치에서 만나기로 결정했지만 조금도 움직이기 싫었던 그들은 어디에서 만나는 것이 본인에게 좋을지 고민에 빠지게 된다. 이때 A가 말했다. “서로에게 동등한 거리에 있는 위치를 고르는 것이 가장 공평하다.” 하지만 B가 말한다. “그것은 우리 모두에게 손해다. 삼각형의 외접원을 생각하면 삼각형의 모양에 따라 삼각형과 외접원의 중심이 충분히 멀리 떨어질 수 있다. 우리가 딱 그런 상황이다. 그럴 바에는 우리 집에서 만나는 것이 훨씬 이득이다.” 이때 C가 말한다. “만약 B의 집에서 만난다면 B는 편안하겠지만 A와 나는 둘이 만나는 것보다 더 많이 움직여야 한다. 이것은 불공평하다.” 이때 A는 묻는다. “어떻게 만나야 서로 손해보지 않고 만나는 걸까?” C가 답한다. “한 사람이 더 편하면 안 된다.” A는 되묻는다. “더 편한 건 어떤 거야?” C가 답한다. “누군가 더 편하다는 것은, 나머지 둘이 약속장소로 오는 길에 먼저 만나서 같이 오는 경우의 수가 하나라도 있다는 뜻이다.” 셋은 그 뒤로 잠시 고민하는데 A 가 새로운 제안을 꺼냈다. “이 도시는 격자형 도로이기 때문에 우리는 서로 손해보지 않고 만나는 방법이 있어!” 과연 A의 말은 사실일까? 격자형 도로는 무슨 연관일까?

A가 생각한 방법은 다음과 같다. 도시의 격자형 도로가 무한하게 존재하여 교차점들이 좌표평면의 정수점에 해당한다고 가정해보자. 만약 A, B, C의 위치가 각각 (3, 0), (-2, -2), (0, 7)이라고 해보자. B가 A나 C, 둘 중 어디든지 가려면 북쪽으로 두 번 이상 움직여야 하며 동쪽으로 두 번 이상 움직여야 한다. 따라서, B는 누구에게 가려면 점 (0,0)을 지나는 것이 유익해 보인다. 그렇다면 A도 같은 입장일까? A의 집에서 B나 C가 있는 곳으로 가려면 적어도 서쪽으로 세 번 움직여야 한다. 하지만 B는 A에서 상대적으로 남쪽에 위치해 있고, C는 A에서 상대적으로 북쪽에 위치해 있으므로 점 (0, 0)에서 갈라지는 것이 가장 좋다. C의 입장에서도 점 (0, 0)까지 가는 길은 A와 B의 집으로 가는 길이기 때문에 점 (0, 0)에서 만나면 불공평하다 느끼지 못할 것이다. 따라서 점 (0, 0)에서 만난다면 서로 손해보지 않고 만날 수 있다. (그림 1)

사실 도시의 도로가 격자형이면 임의로 위치한 세 마을에 대해 가장 좋은 자리는 언제나 존재하며 유일하다. 우리는 이런 성질을 가진 그래프를 중점그래프라 말한다. 엄밀히 정의하자면, 그래프 X의 임의의 세 점 x_1, x_2, x_3에 대해 항상 유일한 점 m이 있어 서로 다른 임의의 i와 j에 대해 점 x_i에서 점 m을 통과하여 점 x_j로 가는 최소경로가 존재하면 우리는 X를 중점그래프라 부른다.

임의의 차원에 대해 유클리드 공간의 정수 격자도 중점그래프이다. 세 개의 정수점 x = (x_1, …, x_n), y = (y_1, …, y_n), z = (z_1, …, z_n)에 대해 m_i를 x_i, y_i, z_i의 중간값(두 번째로 큰 값)으로 정의하면 m = (m_1, …, m_n)은 점 x, y, z의 중점이 된다는 것을 계산할 수 있다. 중점그래프의 또 다른 예는 트리가 있다. 트리의 두 점을 잇는 최소 경로는 유일하다. 트리에서 서로 다른 세 점 x, y, z을 골랐을 때, 그들을 포함하는 가장 작은 부분연결그래프는 삼각대 모양의 트리가 된다. 이때 x, y, z 중 두 점을 잇는 최소경로는 항상 삼각대의 중심을 지나게 되기 때문에 삼각대의 중심은 점 x, y, z의 중점이 된다. (그림 2)

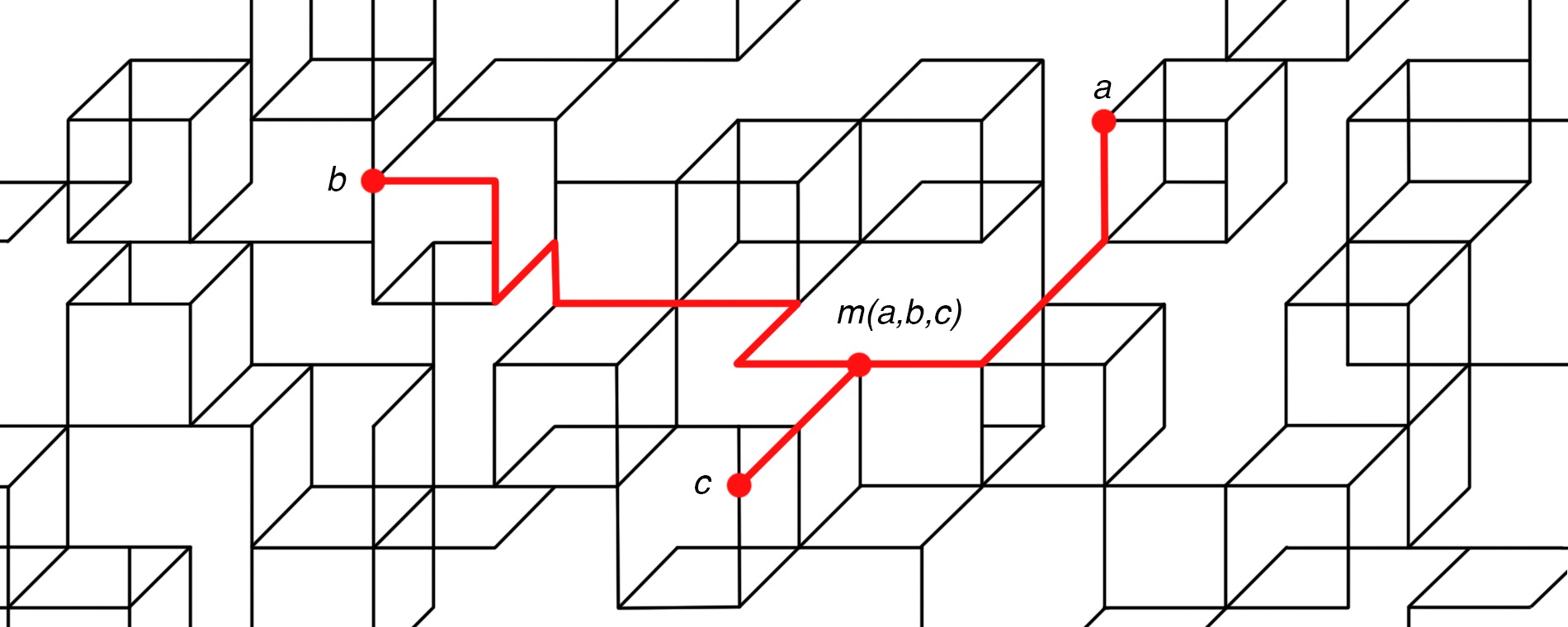
사각그래프는 평면 위의 그래프로서 모든 면이 (볼록)사각형으로 이루어져 있으며 각 점이 적어도 네 개의 변과 연결되어 있는 그래프를 말한다. 오른쪽의 그림은 사각그래프의 한 예로, 무한히 큰 정규 사각그래프이다. 사각그래프는 언제나 중점그래프이다. 세 점의 중점을 찾는 방법은 위의 A가 제시한 아이디어와 유사하다. 세 점을 고르면 어떤 한 점에서 다른 두 점과 동시에 가까워지는 방향으로 최대한 움직인다. 그러면 특정 점에 도달해서는 두 점과 동시에 가까워질 수 없게 되는데 이 점이 세 점의 중점이 된다. (그림 3)

왜 그럴까? 왜 위와 같이 정의하면 세 점의 중점 정의에 부합하는가? 이것을 설명하는 것이 이번 글의 첫 번째 목표이다. 우선 사각그래프의 성질을 살펴보자. 사각형의 서로 마주보는 변들을 서로 평행하다고 정의하자. ^{물론 직사각형이 아닐 수도 있으니 평면 위의 두 직선으로서는 평행하지 않을 수 있다.}  만약 두 변 e(0), e(k)에 대해 어떤 변들의 열 e(0), e(1), …, e(k)이 존재하여 모든 i에 대해 e(i-1)과 e(i)가 평행하면 e(0)와 e(k)가 평행하다고 정의하자. 그러면 변들의 모임에서 평행성은 동치관계가 된다. 어떤 변에 대해 평행한 변들을 전부 모아보면 오른쪽 그림과 같이 생겼다는 것을 알 수 있다. (그림 4)

이때 평면 위에 곡선을 그려 평행한 변들의 중점을 한번씩 만나도록 지나게 할 수 있는데 이것을 변의 수직선이라 부르자. 만약 서로 다른 두 점이 수직선으로 구분된다면 ^{즉, 수직선으로 잘랐을 때 두 점이 서로 다른 연결성분에 들어간다면,} 그 두 점의 최소경로는 수직선을 오직 한 번만 지나게 된다. 여기에서 유도될 수 있는 사실은, 두 점의 최소경로를 생각해보면 경로 위의 모든 변들의 수직선들은 두 점을 구분한다. 반대로, 두 점을 구분하는 수직선은 반드시 두 점의 최소경로와 한번 만난다.

이제 사각그래프가 중점그래프라는 것을 증명하자. 사각그래프에서 임의로 세 점 x, y, z를 고르고 말을 점 x 위에 올려놓자. 위와 같이 말을 점 y, z에 동시에 가까워지도록 움직이는 방법은 점 x와 집합 {y, z}을 구분하는 수직선을 하나씩 건너는 과정이며 말이 멈추는 점 m에서는 더 이상 말과 집합 {y, z}을 구분하는 수직선이 존재하지 않음을 의미한다. 다시 말하면, 점 y로 다가가려면 점 z로부터 멀어질 수 밖에 없고, 점 z로 가까워지려면 점 y로부터 멀어질 수 밖에 없다. 즉, 말이 서 있는 지점 m은 점 y와 점 z를 잇는 최소경로 위에 위치하게 된다. 따라서, 말이 있는 위치인 점 m은 세 점 x, y, z 의 중점이 된다. (그림 5)

그렇다면 점 m은 점 x, y, z의 유일한 중점일까? 임의의 변에 대해 그것의 수직선으로 평면을 잘라보자. 이때 만약 점 x, y가 하나의 연결성분에 포함된다면 점 m은 점 x와 점 y의 최소경로 위에 놓여야 하기 때문에 반드시 점 x, y와 같은 연결성분에 포함되어야 한다. 다시 말하면, 점 m이 포함된 연결성분은 점 x, y, z 중 적어도 두 점을 포함해야 한다. 따라서 중점을 포함하지 않는 연결성분은 점 x, y, z 중 하나 이하만 포함할 수 있다. 점 m이 아닌 임의의 점 w에 대해 점 m과 점 w를 가르는 수직선을 생각해보면 점 w가 포함된 연결성분은 점 x, y, z 중 최대 하나만 포함해야 한다. 따라서 점 w는 중점이 될 수 없다. 그래서 점 m은 점 x, y, z의 유일한 중점이다. 따라서 사각그래프는 중점그래프이다.

이러한 방법은 고차원 공간으로 확장시킬 수 있다. 일반적인 n에 대해 n차원 공간에서 n-차원 큐브들을 적절히 이어 붙인 그래프는 중점그래프가 된다. ^{“적절히 이어 붙인다”는 표현은 전혀 수학적이지 않지만 엄밀한 정의를 위해 몇 가지 정의가 더 필요하다.} 이렇게 만들어진 큐브 그래프에서도 여전히 변들의 평행을 정의할 수 있으며, 변들의 수직면을 정의할 수 있다. 그림 6은 3차원 공간에서 3차원 큐브들을 이어붙여 만든 중점그래프이며, 빨간색 면은 어떤 변의 수직면에 해당한다. 이때 세 점의 중점을 찾는 방법은 앞서 말한 방법과 유사하다.

우리는 지금까지 중점그래프의 예를 살펴보았으며, 중점그래프에서 다루는 간단한 문제에 대해 논의해보았다. 사실 일반적인 중점그래프에서 변의 평행성과 수직면이 정의될 수 있는데, 수많은 연구자들이 평행성과 수직면을 분석하여 중점그래프의 기하학적 특징에 대해 연구하였다. 이를 토대로 1990년 이후로 중점그래프 위에서의 군 작용에 대한 연구가 유행하였고, 그들을 바탕으로 가상 하켄 추측을 해결하게 되었다. [1]  최근에는 복소기하학의 문제를 중점그래프로 분석하는 시도들이 이루어지고 있다. [2][3] 

중점그래프는 매우 오랜 세월 연구되었으며, 그만큼 다양한 분야와 다양한 문제가 걸쳐 얽혀 있다. 첫 문단에서 제시한 예시와 같이 어떤 상황이 중점그래프의 구조를 가지면, 언제나 효율적으로 균형을 찾을 수 있다. [4]  진화생물학에서 계통수^{phylogenetic tree} 의 모든 경우의 수는 언제나 중점그래프 구조를 갖는다는 것이 알려져 있다. [5]  로봇공학에서 중점그래프가 응용된 사례가 있다. [6]