차익거래란 무엇인가? [1]

금융수학은 수학과 경제학을 연결하는 학문으로, 이 분야에서 등장하는 중요한 개념 중 하나로 차익거래^arbitrage라는 용어가 있습니다. 기획재정부에서 제공하는 시사경제용어사전에 따르면 차익거래란 ‘어떤 상품의 가격이 시장 간에 상이할 경우 가격이 싼 시장에서 매입하여 비싼 시장에 매도함으로써 매매차익을 얻는 거래 행위’를 뜻합니다. 이 개념을 쉽게 이해할 수 있도록 다음의 이야기를 살펴봅시다.

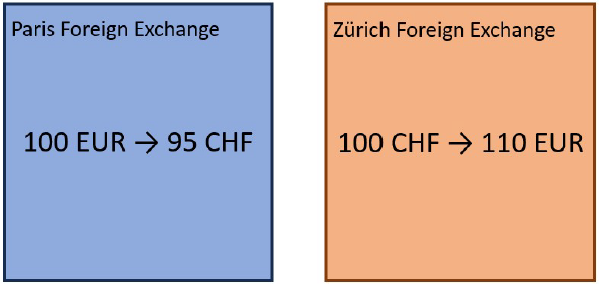
프랑스 파리의 어떤 환전소에서는 100 EUR(유로)로 95 CHF(스위스 프랑)을 살 수 있다고 합니다. 반면에 스위스 취리히의 다른 환전소에서는 100 CHF(스위스 프랑)을 110 EUR(유로)로 환전할 수 있다고 합니다. 만약 이러한 정보를 알고 있는 사람이 있다면, 이 사람은 두 환전소의 환율 차이를 이용하여 손쉽게 돈을 벌 수 있습니다. 예를 들어 이 사람이 파리에 있는 환전소에서 10,000 EUR를 9,500 CHF으로 환전한 후, 취리히에 있는 환전소로 가서 이를 다시 9,500 CHF × 1.1 = 10,450 EUR로 바꾸면 450 EUR만큼의 돈을 벌 수 있는 ‘차익거래’를 할 수 있습니다. 물론 파리와 취리히를 왕복하는 비용(왕복 기차 요금이 평균 222 EUR 정도라고 합니다)이 발생하지만, 위와 같은 차익거래 기회가 영원히 있다면, 이 사람은 이론적으로 무한히 많은 돈을 벌 수 있을 것입니다.

사실 이러한 환율 차이를 이용한 차익거래 기회는 매우 드물게 존재하며, 이런 기회가 있다고 하더라도(안타깝게도) 영원히 지속되지 않습니다. 이 사람이 파리에 있는 환전소에서 더 많은 유로로 스위스 프랑을 구매할수록 – 혹은 이러한 환율 차이가 있음을 알게 된 다른 사람들이 몰려들어 이와 같은 환전을 계속할수록 – 이 환전소의(유로 대비) 스위스 프랑의 가격은 점점 올라가게 됩니다. 반대로 이러한 차익거래가 계속될수록 취리히에 있는 환전소의 유로 가격은 내려가게 되어 결국 두 환전소의 환율 차이가 없게 되는 평형 상태^equilibrium에 이르게 되며 차익거래의 기회는 사라지게 됩니다.

이와 관련하여 경제학자들은 금융시장 안의 모든 정보가 투명하게 공개되어 있고 상품의 가격들이 모두에게 공평하게 책정되어 있다면 차익거래의 기회가 있을 수 없고, 혹은 그러한 기회가 있더라도 위와 같은 차익거래자^arbitrageur들로 인해 가격 차이가 빠르게 사라지고 평형 상태에 이르러 차익거래의 기회가 없어질 수밖에 없다는 차익거래 불가 원칙^{no arbitrage principle}을 생각해 내게 되었습니다.

공짜 점심은 없다

차익거래와 관련하여 ‘공짜 점심은 없다^{there is no such thing as a free lunch}’라는 유명한 문구가 있습니다(there ain’t no such thing as a free lunch라는 문구로 알려진 경우도 있습니다). 누가 먼저 ‘공짜 점심’이란 단어를 사용하였는지는 알려지지 않았지만, 18세기 말 – 19세기 초부터 이 문구가 쓰였다는 기록이 있습니다. 19세기 중반 이후로는 다양한 분야에서 조금씩 다른 의미로 쓰이고 있는데, 자유시장(free market, 상품의 가격이 정부와 외부 권력의 개입 없이 수요-공급에 의해서만 결정되어야 한다는 경제학 이론)을 옹호했던 노벨경제학상 수상자인 밀턴 프리드먼^{Milton Friedman}은 그의 저서에서 기회비용^{opportunity cost}을 묘사하기 위해 공짜 점심이란 단어를 사용했습니다. 공짜처럼 보이는 것이라도 보이지 않는 기회비용이 숨어 있다는 뜻인데, 예를 들어 햄버거를 공짜 점심으로 제공받아 먹는 사람은 무료로 햄버거를 먹는 대신 자신이 더 좋아하는 피자를 점심으로 먹을 기회를 잃는다고 생각할 수 있습니다.

금융수학에서 말하는 공짜 점심이란 초기 자본 없이 시작하여 양의 재산^{positive wealth}을 만들어낼 수 있는 투자 전략을 의미합니다. 따라서 차익거래가 불가하다는 원칙은 때때로 공짜 점심은 없다는 말로 표현됩니다. 위의 두 환전소 이야기에 등장했던 사람이 450 EUR를 ‘공짜로’ 벌기 위해서는 10,000 EUR의 ‘초기 자본’이 필요한 것처럼 보이지만 이 차익거래도 사실은 공짜 점심에 해당합니다. 금융에서는 흔히 돈을 차용하고 갚는 것이 자유롭다는 가정을 하므로 돈이 없는 사람(초기 자본이 0인 사람)도 은행 혹은 그의 친구로부터(추후 얼마의 이자를 내기로 하고) 10,000 EUR를 빌린 후 파리, 취리히를 오가는 두 번의 환전을 통해 10,450 EUR를 만들 수 있습니다. 이후 원래 빌렸던 돈을 갚고 나면 결과적으로 450 EUR에서 왕복 기차비와 이자를 뺀 금액만큼의 ‘공짜 점심’을 만들어냈다고 볼 수 있습니다.

이항 모형 – 가장 단순한 금융 시장

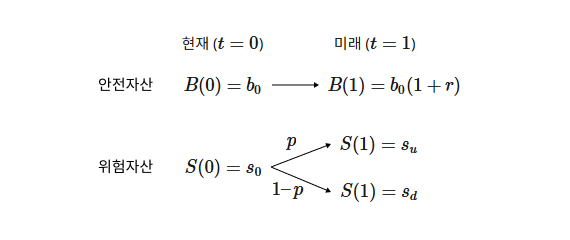
차익거래와 공짜 점심을 조금 더 수학적으로 설명하기 위해 가장 단순한 금융시장 모형^{market model}으로 알려진 이항 모형^{binomial model}을 소개하려고 합니다. 우선 금융시장의 자산들은 안전자산^{riskless asset}과 위험자산^{risky asset}으로 나눌 수 있는데, 이항 모형은 한 개의 안전자산\((B)\)과 한 개의 위험자산\((S)\)으로 이루어진 시장 모형입니다.

안전자산이란 무위험자산으로, 손실 위험이 없고 미래의 가치를 정확히 예측할 수 있는 은행 예금, 국고채^{treasury bond} 등의 자산을 말합니다. 이러한 자산들은 정해진 이자율에 따라 자산의 미래 가치를 미리 알 수 있습니다. 예를 들어 이자율이 \(r\)일 때 현재 \((t = 0)\)의 가치가 \(b_{0}\)인 안전자산은 어떤 단위시간\((t = 1)\) 이 흐른 후에는 가치가 \(b_{0}\)\((1 + r)\)이 됩니다. 반면에 위험자산은 주식(유가증권, stock)과 같이 미래의 자산 가치를 미리 예상할 수 없고, 손실 위험이 있는 자산을 말합니다. 이항 모형은 이 예상할 수 없는 미래의 가치가 두 가지 값만을 가질 수 있다고 단순화시킨 모형으로, 현재 \((t = 0)\) 자산 가치가 \(s_{0}\)인 위험자산이 단위시간 \((t = 1)\) 후의 가치는 \(p\) ∈ \((0, 1)\)의 확률로 \(s_{u}\)가 되거나 1 − \(p\)의 확률로 \(s_{d}\)가 된다고 가정하는 모형입니다. 이때 \(s_{u} > s_{d} > 0 \)의 부등식을 가정하기 때문에 미래의 위험자산의 가치는 \(p\)의 확률로 더 큰 값인 \(s_{u}\)가 되는 경우와 1 − \(p\)의 확률로 더 작은 값인 \(s_{d}\)가 되는 경우밖에 없다고 생각할 수 있습니다.

이러한 이항 모형에서 2차원 벡터 \(\pi\) = \((\pi^{B},\pi^{S}) ∈ \mathbb R^2\)를 포트폴리오^portfolio라고 부르는데, 포트폴리오란 여러 종류의 자산으로 구성된 하나의 혼합자산을 의미합니다. 포트폴리오 \(\pi\)의 각 요소 \(\pi^{B}, \pi^{S}\) 는 현재 \((t = 0)\) 투자자가 다음 미래 시간 \((t = 1)\) 까지 소유하고 있는 안전자산과 위험자산의 개수를 의미합니다. 예를 들어 안전자산과 위험자산이 각각 특정 국고채와 주식일 경우, \(\pi\) = \((2, 3)\)은 투자자가 현재 국고채 2개와 주식 3주를 소유하고 있다는 뜻이고, \(\pi\) = \((2.3,−1)\)은 국고채 2.3개를 보유하고 주식 1주를 누군가에게 빌린 후 팔아버린 상태라고 생각할 수 있습니다. 이렇게 자신이 가지고 있지 않은 자산을 어떤 투자자에게 먼저 빌려서 다른 곳에 판매한 후 다음에 그 자산을 다시 사서 돌려주기로 하는 거래를 공매도^{short selling}라고 합니다. 앞서 말했듯 금융시장에서는 자산을 쉽게 빌리고 빌려줄 수 있다고 가정하기 때문에 \(\pi^{S}\)가 음수가 되는 공매도가 가능하다고 가정하며, 정수^integer가 아닌 실수^{real number}개의 자산을 소유하거나 빌려줄 수 있다고도 가정합니다. 그리고 시간 t일 때 포트폴리오 \(\pi\)의 가치를 \(V^{\pi}(t)\)라고 표기한다면, \(\pi\) = \((2, 3)\)인 경우 현재 포트폴리오의 가치는 \(V^{\pi}(0) = 2b_{0} + 3s_{0} \) , 미래의 가치\(V^{\pi}(1)\)은 \(2b_{0}(1+r) + 3s_{u}\) 또는 \(2b_{0}(1 + r) + 3s_{d} \)가 되는 것을 알 수 있습니다.

이제 위와 같은 이항 모형에서 차익거래를 다음 세 가지 조건을 만족하는 포트폴리오 \(\pi\)라고 수학적으로 정의할 수 있습니다.

1. \(V^\pi(0) = 0\)

2. \(P(V^\pi(1) > 0) > 0\)

3. \(P(V^\pi(1) \geq 0) = 1\)

즉, 초기 자본이 없는 상태(1번 조건)에서 시작하여, 미래에 양의 재산 가치를 가질 확률이 0보다 커야 하며(2번 조건), 동시에 미래에 돈을 잃을 확률이 전혀 없는(3번 조건) 포트폴리오를 차익거래라고 정의합니다. 여기서 1, 2번 조건만을 만족하는 포트폴리오를 흔히 ‘공짜 점심’이라 부릅니다. 따라서 이 시장 모형에서의 차익거래는 ‘손실 위험성이 전혀 없는 공짜 점심’을 의미합니다.

차익거래가 존재할 수 없는 조건

이항 모형에서 차익거래가 존재할 수 없다는 조건^{no arbitrage principle}은 다음 부등식

\[\frac{s_d}{s_0} < 1 + r < \frac{s_u}{s_0} \tag{0.1}\]

이 성립하는 것과 수학적으로 동치^equivalent임을 보일 수 있습니다. 그러므로 부등식 \(\frac{s_d}{s_0} \geq 1 + r\) 또는 \(1 + r \geq \frac{s_u}{s_0}\)가 성립하는 경우에는 차익거래가 존재한다는 것을 보일 수 있습니다.

예를 들어 부등식 \(1 + r \geq \frac{s_u}{s_0}\)이 성립하는 경우를 생각해 봅시다. 이항 모형에서는 위험자산의 미래 가치가 두 가지 값만을 가질 수 있기 때문에 위험자산의 최대 수익률^{growth rate}은

\[\max \left( \frac{S(1) – S(0)}{S(0)} \right) = \max \left( \frac{s_u – s_0}{s_0}, \frac{s_d – s_0}{s_0} \right) = \frac{s_u}{s_0} – 1\]

와 같습니다. 반면 안전자산의 수익률은 항상

\[\frac{B(1) – B(0)}{B(0)} = \frac{B(1)}{B(0)} – 1 = r\]

이기 때문에 부등식 \(1 + r \geq \frac{s_u}{s_0}\)은 위험자산보다는 수익률이 큰 안전자산에 투자하는 것이 더 유리하다는 것을 의미합니다. 따라서 다음과 같이 안전자산 1개를 보유한 대신 위험자산 \(\frac{b_0}{s_0}\)개를 남에게 ‘빌려주는’ (공매도) 포트폴리오

\[\pi = (\pi^B, \pi^S) = \left( 1, -\frac{b_0}{s_0} \right)\]

를 생각한다면, 초기 자산 가치는 \(V^\pi(0) = 1 \times b_0 – \frac{b_0}{s_0} \times s_0 = 0\)이 되어 차익거래의 1번 조건을 만족하게 됩니다. 그리고 미래 (\(t = 1\))의 이 포트폴리오의 가치는 \(V^\pi(1) = 1 \times B(1) – \frac{b_0}{s_0} \times S(1)\)와 같은데, 이 값은 \(p\)의 확률로

\(b_0(1 + r) – \frac{b_0}{s_0}s_u = b_0\left(1 + r – \frac{s_u}{s_0}\right) \geq 0\)

과 같으며 \((1 – p)\)의 확률로

\(b_0(1 + r) – \frac{b_0}{s_0}s_d > b_0(1 + r) – \frac{b_0}{s_0}s_u = b_0\left(1 + r – \frac{s_u}{s_0}\right) \geq 0\)

과 같은 부등식이 성립합니다. 여기에서 마지막 부등식은

\(P(V^\pi(1) > 0) = 1 – p > 0\)

을 의미하므로 차익거래의 2번 조건을 만족하며, 두 부등식을 종합하면

\(P(V^\pi(1) \geq 0) = 1\)

가 성립하여 3번 조건도 성립됨을 알 수 있습니다. 즉, 부등식 \(1 + r \geq \frac{s_u}{s_0}\)이 성립하는 경우 \(\pi = (1, -\frac{b_0}{s_0})\)와 같은 차익거래가 존재한다는 것을 증명할 수 있고, 다른 부등식 \(\frac{s_d}{s_0} \geq 1 + r\)이 성립하는 경우에도 비슷한 방법으로 차익거래가 존재한다는 것을 보일 수 있습니다. 이를 종합하면, 차익거래가 없다면 부등식 (0.1)이 성립해야 합니다.

이제 이 명제의 역^converse을 증명하기 위해 차익거래가 존재한다고 가정하고 이에 해당하는 포트폴리오 \(\pi = (\pi^S, \pi^B)\)를 생각해 봅시다. 그러면 차익거래 1번 조건에 의해 등식

\(V^\pi(0) = s_0\pi^S + b_0\pi^B = 0, \quad \text{또는} \quad b_0\pi^B = -s_0\pi^S\)

이 성립합니다. 이때 \(\pi^S > 0\)이라고 가정한다면, 차익거래 3번 조건에 의해 미래 주식 가격에 상관없이 \(V^\pi(1)\)의 값이 항상 0보다 크거나 같아야 하므로

\[V^\pi(1) = S(1)\pi^S + B(1)\pi^B \geq s_d\pi^S + B(1)\pi^B = s_d\pi^S + (1 + r)b_0\pi^B \geq 0\]

가 성립합니다. 위 등식을 마지막 부등식에 대입하면,

\[s_d\pi^S – (1 + r)s_0\pi^S \geq 0, \quad \text{또는} \quad \frac{s_d}{s_0} \geq 1 + r\]

와 같은 부등식을 얻게 되어 부등식 (0.1)이 성립할 수 없습니다. \(\pi^S < 0\)인 경우도 비슷한 방법으로 부등식 (0.1)이 성립할 수 없음을 보일 수 있고, 이를 통해 차익거래가 존재할 수 없는 조건과 부등식 (0.1)의 동치임을 증명할 수 있습니다. 즉, 안전자산의 수익률 (\(r\))이 위험자산의 최대 수익률 (\(\frac{s_u}{s_0} – 1\))과 최소 수익률 (\(\frac{s_d}{s_0} – 1\)) 사이에 있다면, 이 두 가지 자산만을 이용하여 차익거래를 할 수 없다는 것을 의미합니다.

마치며

첫 부분에 나온 ‘두 환전소 이야기’와 이항 모형에서 부등식 (0.1)이 갖는 의미를 연관 지어 생각해 보면, 차익거래가 없다는 조건은 결국 시장 내의 모든 자산의 가격이 ‘적절한 상태’에 있어야 한다는 것을 의미합니다. 이항 모형과 같은 시장에서 부등식 (0.1)이 성립하지 않는다면, 사람들은 두 자산(안전자산, 위험자산)을 이용하여 차익거래를 만들어 내려 할 것이고, 이러한 거래들이 지속되면 두 자산의 가격이 조정되어 결국 부등식 (0.1)을 만족하는 상태에 이르게 될 것입니다.이번 연재에서는 차익거래가 무엇인지 알아보고, 이것이 수학적으로 갖는 의미를 이항 모형이라 불리는 단순한 금융시장 모형에서 살펴보았습니다. 다음 연재에서는 차익거래 불가 원칙이 적용된 이론 중 가장 널리 알려진 옵션 가격 결정 이론^{option pricing theory}에 대해 소개할 예정입니다.