이 시리즈에서는 여러 공간의 쌍곡성을 살펴보려고 합니다. 이번 글에서는 2차원 물체, 즉 곡면만 집중해서 보겠습니다.
이 세상에는 다양한 곡면이 있는데, 우리가 흔히 아는 평평한 평면도 있고, 지구 표면과 같은 구면도 있고, 말안장 모양과 같은 올록볼록한 모양도 있습니다. 이중에서 말안장 모양의 안장 꼭지 부분을 잘라내 여러 개를 예쁘게 이어 붙이면, “모든 구석이 말안장처럼 일정하게 뒤틀린” 곡면을 만들 수 있습니다. 이런 곡면들을 흔히 쌍곡 곡면hyperbolic surface이라고 부릅니다. 저를 포함해서 많은 수학자들은 이런 쌍곡 곡면을 특히 좋아합니다.
왜 하필 쌍곡 곡면을 좋아하는지 변명(?)을 해 보겠습니다. 사실 모든 구석이 구면과 같이 생긴 구면 곡면spherical surface, 혹은 모든 구석이 평면처럼 생긴 평평한 곡면flat surface 또한 생각할 수 있습니다. 다만, 구면을 잘라 이어 붙이면 사실 구면 자기자신밖에 만들 수 없다는 사실이 알려져 있습니다. 평면처럼 생긴 조각을 이어 붙여 평평한 곡면을 만들면 어떻게 될까요? 이때는 평면 자기자신, 길쭉한 원통, 그리고 도넛 모양 3가지밖에 만들 수 없다는 사실이 알려져 있습니다. 그에 비해, 쌍곡 곡면의 가짓수는 무한히 많습니다. 도넛 두 개를 접합시킨 구멍 두 개짜리 도넛, 구멍 세 개짜리 도넛, 구멍 100개짜리 도넛 등등이 모두 쌍곡 곡면으로 나타납니다. 따라서 어떤 의미에서 보면 “가장 일반적인” 곡면을 공부하고 싶다면 쌍곡 곡면을 고르는 게 적절하다고 볼 수 있습니다.
이제 쌍곡 곡면을 공부하는 다른 관점을 소개하겠습니다. 쌍곡 곡면은 아니지만 원통을 먼저 예로 들어 보죠. 원통 모양은 평면의 일부분인 정사각형 타일을 이어 붙여 만들 수 있기도 하지만, 평면을 둥글게 말아 여려 겹을 포개어도 만들 수 있습니다. 이렇게, 커다란 원단을 적절한 방식으로 말아서 포개었을 때 크기가 더 작은 물체를 만들 수 있는데, 쌍곡 곡면들 또한 이런 방식으로 만들 수 있습니다. 실은, 모든 쌍곡 곡면들을 만들어 낼 수 있는 아주 커다란 원단이 존재합니다. 이 원단 역할을 하는 곡면이 바로 쌍곡평면hyperbolic plane이라고 불리는 것입니다. 어떤 의미에서, 쌍곡평면을 말아서 포개는 “재단하는 방식”만 잘 이해하면 모든 쌍곡 곡면을 이해한다고 볼 수 있을 것입니다. 그렇기에 수학자들은 쌍곡평면과 그 등거리사상 군을 오랫동안 연구해 왔습니다. 예전에 제가 연재한 만화에서 이 관점을 더 자세히 보여주고 있으니 참고하셔도 좋을 것 같습니다.
그러면 쌍곡평면을 들여다 보겠습니다. 쌍곡 곡면의 수학적인 정의는, 3차원 좌표공간에서 두 쪽짜리 쌍곡면hyperboloid을 생각한 뒤 그중 한 쪽만 택한 것입니다. 수식으로 나타내면
$$S = \big\{ (x, y, t) : t^{2} – (x^{2} + y^{2}) = 1, t \ge 0\big\}$$
라는 집합이 됩니다. 다만 이 집합만 선언했다고 해서 쌍곡 곡면이 건설된 것은 아닙니다. 곡면이 실제로 어떤 형태로 굽어 있는지를 이해하기 위해서는 점들 간의 멀고 가까움을 얘기할 수 있어야 합니다. 즉 거리 구조metric를 얹어 주어야 합니다. 그림 1에서는 3차원 유클리드 공간 안에 집합 $S$가 어떻게 놓여 있는지를 보여주는데, 이 그림은 $S$를 왜곡해서 보여주고 있습니다. 즉, $S$를 우리가 원하는 쌍곡 곡면으로 구현하기 위해서는 3차원 유클리드 거리 말고 다른 거리를 얹어 주어야 합니다.
이제 우리에게 새로운 질문이 생겼습니다. 어떤 수학적인 집합 $S$가 있을 때, 그림으로부터 바로 보이는 “겉보기 거리” 말고 새로운 거리 구조를 $S$에 얹어 주려면 어떻게 해야 할까요? 리만 기하학 수업 시간이었다면, 리만 계량Riemannian metric이라는 것을 $S$ 위에 정의하는 것으로 시작했을 것입니다. 실제로 집합 $S$를 쌍곡평면으로 만드는 가장 정확한 방법이 리만 계량을 이용한 것입니다. 하지만 이번 시간에는 꼼수를 써 보겠습니다.
앞에서, 쌍곡 곡면이란 어떤 특정한 타일을 예쁘게 이어 붙인 것이라고 했습니다. 그 이어 붙인 패턴을 $S$ 위에 표시해 보면 어떻게 보일까요? 동일한 모양의 타일이 $S$의 구석구석에 어떻게 붙어 있는지를 눈으로 보면, $S$에 어떻게 거리 구조를 구현할지 감이 잡힐 것 같습니다. 그림 1의 쌍곡곡면은 이미 타일링이 되어 있는데, 유클리드 공간에서 바라본 이 타일링은 상당히 왜곡되어 있죠. 게다가 모든 타일들이 표시된 것도 아닙니다. 사실 쌍곡면은 그림에서 보이는 것보다 훨씬 더 크게, 무한히 많이 뻗어 있어야 하는데, 우리 시야는 유한하니 이렇게밖에 그리지 못한 것입니다. 따라서, 무한히 많은 타일들을 다 담기 위해 쌍곡평면을 바라보는 다양한 시각이 등장했습니다. 그중 하나가 바로 푸앵카레H. Poincaré의 모델입니다. 이 모델은 $z$축 위에서 원점으로부터 1만큼 아래에 있는 점 $(0, 0, -1)$에서 쌍곡면을 바라봤을 때 보이는 장면을 택한 것인데요, 쌍곡면 위의 모든 부분이 $xy$평면상의 반지름 1짜리 원에 다 담기게 됩니다. 이 모델에서 타일링이 어떻게 보이는지 그려 보면 그림 2와 같습니다.
이러한 패턴을 어디선가 보셨다면, 에셔M. C. Escher의 그림이었을 가능성이 있습니다. 미국 National Gallery of Art에는 에셔의 작품 “Circle Limit I”가 전시되어 있는데, 링크는 다음과 같습니다. https://www.nga.gov/artworks/54281-circle-limit-i
그림 2의 타일링을 조금 더 큰 단위로 보면 육각형을 이리저리 이어붙인 것으로 생각할 수 있습니다. (그림 3) 쌍곡평면 말고 평면 또한 육각형으로 타일링이 가능합니다. (그림 5 참조) 다만 평면에서는 한 꼭짓점당 육각형이 세 개씩 붙지만 쌍곡평면에서는 한 꼭짓점당 육각형이 네 개 이상씩 붙습니다. 이 작은 차이가 두 공간의 성질을 크게 좌우한다는 것을 곧 살펴볼 것입니다.이제 쌍곡평면 $S$에 적절한 거리를 정의하는 작업으로 되돌아 갑시다. 그림 4와 같이 점 $A$와 점 $B$가 주어졌다고 해 봅시다. $A$로부터 $B$까지 갈 때 가로질러야 하는 최소 타일 수를 $A$-$B$간의 “타일 거리”라고 부르겠습니다. 여기서는 $A$와 $B$ 사이의 거리가 9입니다. 이제 그림과 같이 점 세 개 $A$, $B$, $C$가 주어졌을 때 $A$와 $B$ 사이 거리 및 $B$와 $C$ 사이 거리의 합이 $A$와 $C$ 사이 거리보다 크거나 같다는 것을 알 수 있습니다. 즉, 삼각 부등식이 성립함을 알 수 있습니다.
이렇게 정의한 거리는 유클리드 평면상의 원판으로서 가지는 “겉보기 거리”와는 매우 다릅니다. 유클리드 거리에서는, 원판의 중심으로부터 가장자리까지 이르는 데 거리 1밖에 걸리지 않습니다. 하지만 타일 거리에서는 어떨까요? 다시 보니 우리 타일링에서는 가장자리로 다가가면 다가갈수록 타일이 더 촘촘하게 박혀 있다는 것을 알 수 있습니다. 이 때문에, 타일 유한 개만 가로질러서 원점으로부터 가장자리까지 가는 방법이 없습니다. 즉 타일 거리 n인 점들을 모아 보면 모두 가장자리 원보다 안쪽에 그려진다는 것을 알 수 있습니다. 따라서 원점으로부터 가장자리까지의 타일 거리는 무한대입니다. 즉, 이 조그마한 원판은 유클리드 평면만큼이나 거대한 것입니다.
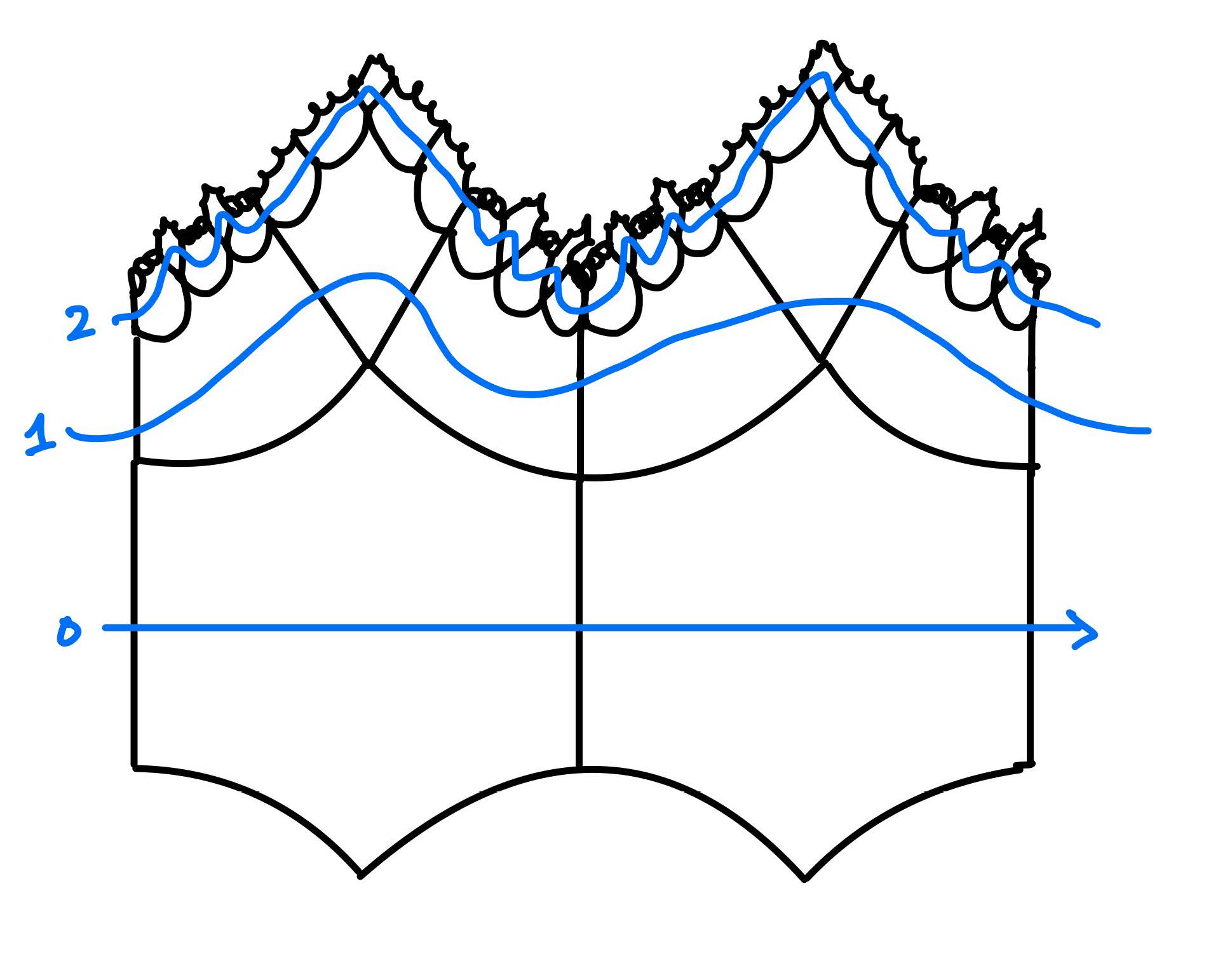
더 신기한 성질은, 이 공간 위에서는 그 어떤 삼각형도 항상 “얇다”는 것입니다. 이를 설명하기 위해 점 A, B, C를 다시 살펴 봅시다. 이때 $d(A, C)=8, d(A, B) = 9$ 및 $d(B, C) = 10$입니다. 이때 $A$에서 $C$로 가면서 가장 적은 갯수의 타일을 지나려면 파란색 선을 따라가야 합니다. 마찬가지로 빨간색 선 및 초록색 선은 각각 A와 B 사이의 최단 타일 경로, 그리고 B와 C 사이의 최단 타일 경로를 나타냅니다. 이때 파란색 선은 마치 나머지 두 선의 궤적을 좇아가듯 그려집니다. 빨간색 선 및 초록색 선이 지나지 않는 타일은 파란색 선이 지나지 않습니다. 즉, 빨간 타일 경로와 초록 타일 경로를 합집합하면 파란 타일 경로를 완전히 포함하게 됩니다.
이 현상의 이유를 대강 설명하자면 이렇습니다. 만약 빨간색 선 및 초록색 선으로부터 일부러 멀리 돌아가는 파란색 점선을 파란색 실선 대신으로 쓰려고 하면 어떤 일이 생길까요? 빨간색 선 및 초록색 선으로부터 멀어지면 멀어질수록 타일의 (겉보기) 크기가 엄청 작아져, 지나야 하는 타일 갯수가 엄청나게 늘 것입니다. 따라서 파란색 점선은 파란색 실선보다 훨씬 비효율적이기에, 최단 경로로서 대역이 될 수 없습니다. 더 구체적으로, 아래 그림 5에서 0단계 선이 가장 효율적인 선, 즉 최단 경로라면, 여기서 조금 더 멀리 벗어나면 벗어날수록 지나는 타일 갯수가 기하급수적으로 증가합니다. (비유가 아니라, 정말 기하급수적으로 증가합니다!) 이러한 현상은 평면의 정육각형 타일링에서는 발생하지 않습니다. (그림 6) 오히려, 최단 경로 선에서 아무리 멀리 떨어진 곳에서도 평행한 다른 최단 경로를 찾을 수 있습니다. 즉, 쌍곡평면에서는 둘다 최단 경로=직선이면서 평행한 두 녀석을 찾을 수는 없지만, 유클리드 평면에서는 그럴 수 있다는 점이 숨겨진 이유라고 할 수 있습니다.
다시 삼각형 ABC로 돌아와 봅시다. 파란 타일 경로뿐 아니라, 빨간 타일 경로 및 초록 타일 경로 또한 나머지 두 타일 경로의 일부분을 따라가고 있습니다. 이처럼, 이렇게 점 A, B, C를 잇는 “타일 경로” 삼각형을 그렸을 때, 각 변이 나머지 두 변 근처를 계속 머물고 있습니다. 이 관찰을 토대로 다음과 같은 개념을 한번 구성해 봅시다.
정의. 어떤 거리 공간이 “상당히 날씬하다”는 것은, 어떤 유한한 상수 $D$가 존재해 다음이 성립한다는 뜻이다. (1) 임의의 두 점 사이에 최단 거리 경로를 그을 수 있다. (이는 곧 두 점 사이의 `선분’ 역할을 하는 물체가 있다는 뜻이다.) (2) 임의의 세 점이 주어졌을 때 각 두 점간의 최단 거리 경로를 그려 만든 삼각형을 생각했을 때, 각 변은 다른 두 변의 합집합으로부터 거리 $D$ 이하인 영역에 머물러야 한다.
그러면 타일 거리가 주어진 쌍곡평면은 상당히 날씬함을 알 수 있습니다. 그에 반해, 우리가 흔히 아는 유클리드 평면이나 유클리드 3차원 공간은 상당히 날씬하지는 않음을 알 수 있습니다. 한 변의 길이가 $R$인 정삼각형의 한 변 위에는 다른 두 변으로부터 거리 $R/4$ 이상에 있는 점(예를 들어 중점)이 존재하고, $R$은 임의의 양수 값을 가지기에 유한한 상수로 제한할 수 없기 때문입니다. 또, 유클리드 평면에 앞에서 말한 정육각형 타일링을 생각한 뒤 타일 거리를 얹었다고 해도, 상당히 날씬하지는 않음을 확인할 수 있습니다.
이것으로 쌍곡평면은 날씬하고 유클리드 평면은 뚱뚱하다는 결론을 지을 수 있다면 행복한 얘기겠지요. 하지만 한 가지 짚고 넘어갈 점이 있습니다. 이 “타일 거리의 상당히 날씬함”이라는 성질은, 단위 타일의 선택지에 의존하지는 않는지입니다. 예를 들어 위 예시에서는 쌍곡평면 및 유클리드 평면의 정육각형 타일링을 활용한 것입니다. 즉 타일 거리 = 최단 “정육각형” 타일 경로의 길이인 것이죠. 하지만 정육각형 타일을 12등분한 직각삼각형 타일을 사용하면, 타일 거리가 달라지게 됩니다. 정육각형 타일 거리가 10인 두 점이 있을 때, 직각삼각형 타일 거리는 최소 10, 최대 50까지 이를 수 있습니다. 이렇게, 어떤 타일을 사용했는지에 따라 거리가 들쭉날쭉해지는데, “공간의 상당히 날씬함” 또한 이 타일의 선택지에 의존할 여지가 있지 않을까요?
여기서 한 가지 고백하자면, 지금 얘기하고 있는 “상당히 날씬함”은 사실 제가 멋대로 부른 이름이고, 원래 이름은 따로 있습니다. 바로 Gromov 쌍곡성이라는 것입니다. 1980년대 M. Gromov는 (여기서는 제대로 도입하지 않았지만) 쌍곡평면에 자연스러운 리만 계량 거리 구조를 얹으면 상당히 날씬하다는 사실을 관찰하고, 이것이 쌍곡평면뿐만 아니라 d차원 실-쌍곡 공간real hyperbolic space, 더 나아가 곡률에 음수 상한이 있는 축약 가능한contractible 리만다양체 모두가 이 성질을 가짐을 관찰했습니다. 하지만 여기에서 그치지 않고 Gromov는 다음 정리를 발견했습니다.
정리. 어떤 (연결된) 거리 공간 $X$을 다 덮을 수 있는 “타일” 두 개를 생각하자. 이때, 한 타일 거리를 기준으로 $X$가 Gromov 쌍곡적이라면, 다른 타일 거리를 기준으로도 $X$는 Gromov 쌍곡적이다.
따라서, 어떤 거리 공간의 Gromov 쌍곡성을 얘기할 때는 타일의 선택지 혹은 타일의 구체적인 모양은 중요하지 않습니다. 타일이 어떤 패턴으로 붙어져 있는지로부터 공간의 쌍곡성을 논할 수 있는 것입니다. 예를 들어, 같은 육각형 모양의 타일이라고 하더라도, 한 점에서 타일 세 개를 붙일지 혹은 네 개를 붙일지에 따라, “평행선 공리가 성립할지 하지 않을지”가 결정되었고, 이것이 곧 쌍곡성을 결정한 것입니다. Gromov의 쌍곡성에 대한 더 깊은 논의는 백형렬 교수님의 이전 글에서 찾아볼 수 있습니다. 또, Gromov 쌍곡적인 공간에는 자연스러운 경계boundary를 정의할 수 있는데, 이것의 성질은 김상현 교수님의 이전 글에 설명되어 있습니다.
이제 추상적인 얘기를 잠깐 하고 1부를 마치겠습니다. 위에서 타일을 “이어 붙이는” 과정을 얼버무렸는데, 이를 구체적으로 기술하는 데는 추상대수학의 기본 개념인 군(group)이 필요합니다. 예를 들어, 그림 에서 쌍곡평면을 직각삼각형으로 타일링하는 과정은
$$G = \langle r_{1}, r_{2}, r_{3} | r_{1}^{2} = r_{2}^{2} = r_{3}^{2} = id, (r_{1}r_{2})^{6} = id, (r_{1}r_{3})^{2} = id, (r_{2}r_{3})^{4} = id \rangle$$
라는 반전 군reflection group을 이용해 설명할 수 있습니다. 반전 군에 관한 더 자세한 얘기는 이계선 교수님의 글에서 찾아볼 수 있습니다.
사실은 그 역 또한 성립합니다. 모든 군에는 그에 꼭 맞는 공간 및 타일링이 있습니다. 다만, 이 타일링 자체는 군의 생성 집합generating set에 의존하기는 합니다. 하지만 앞에서 말했듯 공간의 Gromov 쌍곡성은 구체적인 타일의 선택지에 의존하지 않는 성질이기에, “어떤 군이 Gromov 쌍곡적이다”라는 명제는 (생성 집합에 의존하지 않는) 군의 고유한 성질이 됩니다. 따라서, Gromov가 제안한 의미에서의 “쌍곡군hyperbolic group“을 공부할 수 있습니다. 이것이 현대의 기하군론의 주요한 토대 중 하나입니다.
다음 시간에는 군의 쌍곡성이 구체적으로 무엇인지 예시와 반례를 통해 알아보겠습니다. 특히, 엄밀하게는 쌍곡적이지는 않지만 여전히 약간의 쌍곡성을 띠는 군들을 만나보겠습니다.