1. 여는 글
카페 한구석에 앉아 커피잔을 들여다본 적 있으신가요? 잔 속에서 빛줄기가 벽에 부딪히고, 다시 흩어져 이쪽저쪽으로 퍼져 나가는 순간 말입니다. 가만히 바라보면 그저 예쁜 무늬일 뿐인데, 수학자의 눈에는 어느새 작은 당구대가 펼쳐집니다.
“커피잔에서 당구라니, 말도 안 되잖아요.” 고개를 갸웃할지 모르겠습니다. 하지만 수학에서 말하는 당구는 우리가 흔히 떠올리는 네모난 테이블 위의 묵직한 공만을 가리키지 않습니다. 그 세계에서 당구대는 원이 될 수도 있고, 삼각형이 될 수도 있으며, 심지어는 매끄럽게 휘어진 곡선이 될 수도 있습니다. 공 또한 더 이상 둥글고 무거운 물체가 아닙니다. 마찰도, 둔감한 무게도 없이 그저 하나의 점으로, 일정한 속력으로 직선을 따라 움직이다가 벽을 만나면 단 하나의 규칙에 따라 방향을 바꿉니다. 입사각과 반사각이 서로 같다는, 단순하면서도 변치 않는 규칙이지요.
놀라운 것은 이 단순함이 만들어 내는 풍경입니다. 무수히 부딪히며 이어지는 점의 궤적은 예측할 수 없을 만큼 복잡합니다. 그 안에 숨은 질서를 찾고, 그 질서가 품고 있는 이야기를 읽어 내는 것, 그것이 바로 당구Billiard라는 수학입니다. 다시 커피잔 속 빛줄기를 떠올려 보시겠습니까. 여러 궤적이 겹쳐지며 특정한 영역을 환히 감싸고 있던 모습, 그것은 우연이 아니며, “유일 에르고딕성” 이라는 오늘 이야기할 수학적 개념과도 맞닿아 있습니다.
호라이즌에 백형렬 교수님께서 쓰셨던 ``자유를 원한다면 탁구를 쳐라”라는 제목의 글이 있습니다. 그것을 오마주하여 수학자들의 또 다른 스포츠, 당구에 대해 이야기해 보려 합니다. 그 첫 번째 이야기는 ‘당구와 재규격화’입니다. 작은 빛줄기 하나가 수학의 거대한 풍경으로 이어지는 길을, 함께 걸어가 보시지 않겠습니까.
2. 당구흐름
커피잔 속에서 반짝이던 빛줄기, 수학자들은 그것에 정식으로 이름을 붙였습니다. 바로 당구흐름Billiard flow 입니다.
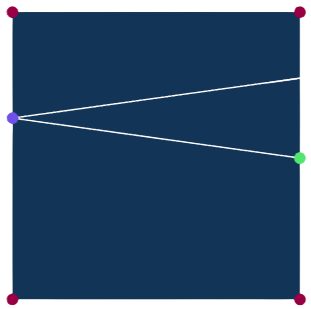
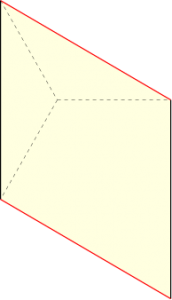
그림 3 과 같이 커피잔과 비슷하게 매끄럽게 휘어진 벽면을 가진 곡선형 당구대를 하나 두고, 그 위에 작은 공을 올려놓는 것을 상상해 보겠습니다. 초록색 점에서 보라색 점을 향해 공을 굴리면, 부딪히기 전까지는 똑바로 나아가겠지요. 벽에 닿는 순간이 오면, 무슨 일이 일어날까요? 매끄러운 벽에서는 충돌 지점에서의 접선을 생각할 수 있습니다. 그리고 공은, 그 접선을 기준으로 입사각과 반사각이 같다는 법칙을 따라 방향을 바꾸어 나아갑니다.
수학자들은 이 과정을 기호로도 담아 둡니다. 당구대 $X$ 위에 있는 공의 출발점을 $p$라 하고, 시간이 $t$만큼 흐른 뒤 공이 도달한 위치를 $\phi_t(p)$라 합시다.
그러면
\begin{align}\label{eq.flow}
\phi_t: X&\to X,\\
p&\mapsto\phi_t(p) \notag
\end{align}
(2.1)
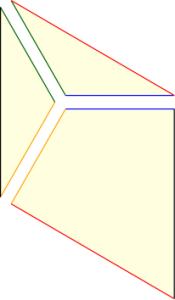
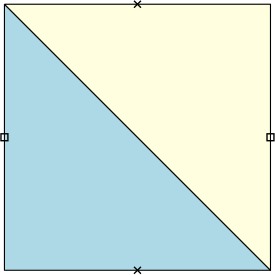
이렇게 쓰는 함수 하나가, 당구대 $X$ 위에서 벌어지는 당구흐름 전체를 정의해 줍니다. 하지만 오늘 우리가 머물려 하는 곳은 곡선형 당구대가 아닌 유리각 당구대rational billiard 입니다. 이름이 다소 낯설지요? 유리각 당구대란 모든 벽면이 곧은 선분으로 이루어져 있고, 그 선분들이 만나는 각이 $\pi$의 유리수배가 되는 당구대를 말합니다. 가장 친숙한 예는 네모난 사각형 당구대이고, 조금 더 변화를 주면 L자, Z자 모양 당구대, 육각형 당구대도 가능합니다.
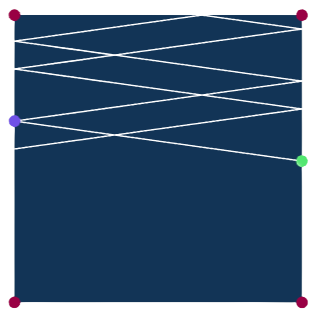
유리각 당구대에서도 공이 진행하는 원리는 전과 동일합니다. 공은 일정한 속도로 직선을 따라가다가, 벽과 충돌하면 반사되어 다른 방향으로 나아갑니다. 그림 5 의 사각형 당구대를 $X$라고 불러 봅시다. 초록색 점에 공을 놓고 보라색 점을 향해 굴린다면, 공의 궤적은 곧은 선을 따라 이어질 것입니다. 그리고 벽에 부딪힐 때마다 공은 계속해서 방향을 바꾸지요. 수학적으로는 똑같습니다.다만 곡선형 당구대에서는 없었던 문제가 생기는데요, 공이 정확히 당구대의 모퉁이를 맞힌다면 더 이상 그 진행방향을 알 수 없다는 점입니다. 당구대의 벽면 중 모퉁이처럼 뾰족한 곳에서는 접선이 정의되지 않기 때문이지요. 그래서 우리는 앞으로의 논의에서 이런 공의 경로들을 모조리 제외하게 됩니다. 공이 모퉁이를 맞힐 수학적 확률은 0이어서, 이렇게 하여도 유리각 당구대의 당구흐름을 정의하는 데에는 어떤 문제도 일어나지 않게 됩니다.
3. 유일 에르고딕성
주어진 당구대 위에서 당구흐름을 정의하기 위해 필요한 정보는 하나입니다. “어느 각도로 공을 출발시킬 것인가?” 바로 그 선택이지요. 각도를 정하고 나면, 자연스러운 질문이 떠오릅니다.
• 당구공의 위치를 오랜 시간에 걸쳐 관측하면 어떤 분포를 얻게 될까?
이 질문을 두 부분으로 더 나눠서 생각해 보겠습니다.
(a) 당구공이 언젠가는 당구대 안의 모든 영역을 지나게 될까?
(b) 만약 그렇다면, 당구대의 특정 위치만을 계속 관측했을 때, 그 곳에서 당구공이 발견될 확률은 위치와 상관없이 균일할까?
통계적인 답을 위해 사진기를 이용할 수도 있습니다. 별의 일주운동을 담기 위해 사용하는 바로 그 방법입니다. 하늘 한쪽을 향해 뒷산에 고정시켜둔 사진기를 잠시 빌려오겠습니다. 그 사진기를 당구대 위 당구흐름을 향하게 한 뒤 장시간 노출시킵니다.
이제 촬영한 사진 속 당구대를 들여다 봅시다. 점들이 비어있는 곳 없이 찍혀있다면 (a)에 대해 그렇다고 답할 수 있을 것이며, 점들의 밀도가 균일하다면 (b)에 대해 그렇다고 답할 수 있겠습니다.
약간 더 기술적인 문제를 생각하기 전에, 중요한 사실 하나를 떠올리려 합니다. 당구흐름에서 공의 움직임은 평행이동과 반사 두 가지로 이루어지는데, 둘 다 면적을 바꾸지 않는 변환이라는 것입니다. 그래서 당구흐름 역시 면적, 즉 르베그 측도를 보존하게 됩니다.
그렇다면 아래와 같은 물음도 던져볼 수 있습니다.
(c) “당구흐름이 보존하는 측도는 오직 르베그 측도뿐일까?”
만약 이 질문에 그렇다고 답할 수 있다면, 우리는 그 흐름이 유일 에르고딕성unique ergodicity을 가진다고 부릅니다. 이 성질은 조금 낯설게 느껴질 수도 있지만, 앞서 제기한 두 가지 질문에 대한 긍정적인 답 – (a) 당구대 위 모든 영역을 지나게 되는 것, 그리고 (b) 당구공이 모든 위치에서 동등한 확률로 발견되는 것 – 을 갖는 것보다 더 강한 조건임이 알려져 있습니다.1
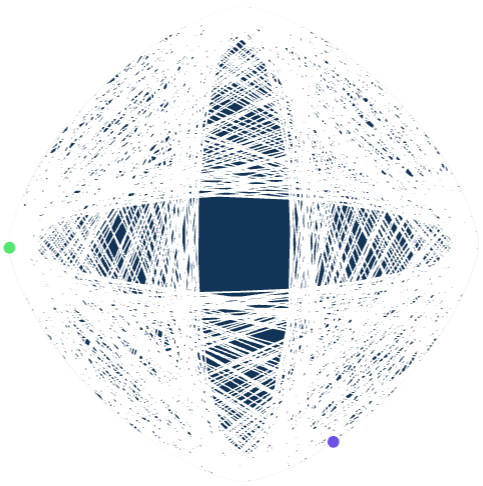
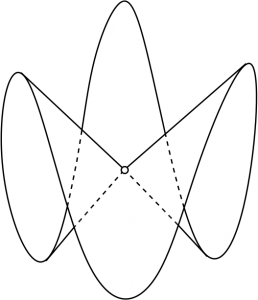
흥미롭게도, (c)에 대한 답은 당구대의 모양에 따라 전혀 다르게 나타납니다. 먼저 볼록하고 매끄럽게 휘어진 곡선형 당구대를 떠올려 보겠습니다. 원형이나 타원 같은 모양 말입니다. 이 경우 어떤 일이 생길까요? 어쩌면 공의 궤적은 당구대 전체를 채우지 못하고, 특정 영역만을 감싸며 맴돌게 될 수 있습니다. 그림 1의 잔 속 무늬와 같은 “포락선”을 형성하면서 말이지요.
이 현상은 다음 사실과 맞닿아 있습니다.
정리 3.1 [라주킨Lazutkin]2 볼록하고 매끄러운 곡선형 당구대는, 당구흐름으로부터 형성되는 포락선을 매우 많이 갖는다.
이 결과는 볼록하고 매끄러운 곡선형 당구대 위에서 유일 에르고딕성이 어떻게 어긋날 수 있는지를 잘 보여 줍니다. 원형 커피잔 안에서의 당구흐름을 떠올려 보면, 궤적은 사진 속 포락선 내부로는 결코 들어갈 수 없었습니다. 즉, 당구흐름이 포락선을 형성한다는 것은 그 당구흐름이 닿을 수 없는 지역이 생겨버린다는 뜻입니다. 따라서 이런 현상이 너무나 빈번히 일어난다면, 당구대의 모든 영역에 이르게 되는 성질 (a)는 기대할 수 없고, 당연히 그보다 강한 성질인 유일 에르고딕성 (c) 역시 성립할 수 없게 됩니다.
이와 대조적으로, 유리각 당구대에서는 거의 정반대의 현상이 나타납니다. 이를 나타내는 것이 바로 다음 정리입니다.
정리 3.2 [커르코프–메이저–스마일리Kerckhoff–Masur–Smillie]2 유리각 당구대 위에서, 거의 모든 각도의 당구흐름은 유일 에르고딕성을 갖는다.
즉, 유일 에르고딕성은 볼록하고 매끄러운 곡선형 당구대에서는 쉽게 무너질 수 있지만, 유리각 당구대에서는 오히려 일반적인 경우에 성립한다는 것입니다. 그림 6의 당구대와 그림 7의 당구대를 나란히 비교해 보시면, 이 두 세계의 대비가 한눈에 들어올 것입니다. 전자에서는 도달할 수 없는 “금지 영역”이 생기지만, 유리각 당구대에서는 거의 모든 경로들이 당구대 전 영역을 고르게 채우게 됩니다.
이번 화에서는 이제 곡선형 당구대의 이야기는 그만 독자분들의 직관과 그림에 맡겨 두고, 대신 유리각 당구대에 초점을 맞추어, 커르코프-메이저-스마일리 정리와 연결된 두 가지 새로운 정리를 소개하려 합니다. 그리고 그 과정에서 자연스럽게 재규격화renormalization 라는 아이디어를 만나게 될 것입니다.
4. 재규격화
| All that is gold does not glitter, 황금이라고 다 반짝이진 않으며, Not all those who wander are lost. 방랑하는 자라고 다 길잃은 것은 아니다. |
—B. Baggins
톨킨의 소설 반지의 제왕 속에서 이 시구는 아무것도 가진 것 없어 보이던 한 인물의 가치를 예언합니다. 그러나 수학자의 눈에는 이 메시지가 마치 동역학계에 등장할 재규격화라는 아이디어를 오래전부터 예견하고 있었던 것처럼 느껴집니다.
재규격화라는 말은 물리학과 수학에서 여러 의미로 쓰입니다. 그것이 양자역학계에 나타나는 이야기는 성기훈 교수님의 글 “재규격화와 파인만 다이어그램”에서 자세히 소개되었습니다. 여기에서는 대상이 되는 동역학계를 바꾸어, 재규격화의 또 다른 일면에 대해 이야기하려 합니다.
4.1 앵무새의 신조
여기 한 마리의 앵무새가 있습니다. 앵무새는 이상한 주문을 되뇌입니다.
“계 $X$ 위의 흐름의 비밀을 알고 싶다면, $X$ 하나만 응시하지 말고, $X$를 그것을 품은 더 큰 우주 $M$의 별로서 바라보아라. 만약 우주 $M$ 위의 흐름 속에서 그 안의 많은 별들이 회귀recur 한다면, 네가 찾는 비밀도 머지않아 눈앞에 드러나리라.”
이것은 마치 수수께끼 같습니다. 우리는 주문 속 `계 $X$ 위의 흐름’에 `당구대 위 당구흐름’이라는 더 구체적인 상황을 대입한 뒤 앵무새가 의미하는 바를 찬찬히 헤아려 보겠습니다.
먼저 당구대 $X$를 고정해봅시다. 그리고 나서 $M$은, $X$를 원소로 갖는, 이 세상의 모든 당구대들이 모여있는 우주라고 해석해 보겠습니다.
그렇다면 $M$ 위의 흐름이란 무엇일까요? $X$ 위의 당구흐름(2.1) 당구공의 움직이는 규칙 $\phi_t: X\to X$ 이었다면, $M$ 위의 흐름은 당구대가 자기들만의 우주 속에서 어떻게 움직이는지를 알려주는 또 다른 규칙 $\Phi_t: M\to M$ 일 것입니다.
하면, 지금 $M$ 위의 모든 당구대들은 어떤 미지의 규칙 $\Phi_t:M \to M$에 따라 끊임없이 움직이고 있는 상황인 것이지요. 그리고 그 와중에 어떤 당구대들은 원래 출발했던 자리로 돌아오는 행위를 무수히 많이 반복하고 있을지도 모릅니다. 우리는 이런 당구대들을 회귀하는 당구대라고 부르겠습니다.
이제 주문의 마지막 구절은, 우리가 당구대들의 우주 $M$ 속에서 회귀하는 당구대들을 많이 발견하면 할수록, 그것들은 우리에게 $X$ 위의 당구흐름, 즉 내 당구공의 경로에 대한 비밀4도 밝혀줄 것이라는 얘기가 됩니다.
우리가 궁금해했던 것은 분명 내 당구공이 어떻게 움직일까 하는 것이었지요. 하지만 앵무새는 이상하게도, 당구공의 움직임 $\phi_t$가 아닌 당구대의 움직임 $\Phi_t$를 바라보라고 하고 있었습니다.
4.2 당구대를 친다는 상상
당구대 위에서 공을 치는 것은 익숙합니다. 그런데 앵무새는 정반대의 상상을 요구합니다. 공이 아니라, 당구대 자체를 쳐보라는 것입니다. 현실이라면 터무니없는 소리겠지요. 실제로 당구대를 치면 아무 일도 일어나지 않고, 오히려 큰 변상을 하게 될 것입니다. 하지만 앵무새의 세계에서라면 다릅니다. 그곳에서는 당구대가 충격을 받아 변신로봇처럼 형태를 시시각각 바꾸기 시작하는데, 이것이 바로 당구대가 그의 세계 $M$ 속을 떠돌아다니는 방법 $\Phi_t$입니다.
당구대가 이리저리 늘어났다 줄어들며 모습을 바꾸다가, 마침내 원래의 형태로 돌아오는 장면. 우리는 그런 그림을 머릿속에 그릴 수 있습니다. 그것이 바로 앵무새가 꿈꾸는 재규격화의 우주입니다. 당구대들이 모여 하나의 공간을 이루고, 그 공간 안에서 떠돌던 당구대가 끝내 원래 모습으로 돌아오기를 반복한다면, 그 반복되는 과정5이 원래 주어진 흐름의 비밀을 드러내는 렌즈의 역할을 수행하게 됩니다.
우리는 이제 이 앵무새의 목소리를 따라가려 합니다.
그러나 조금 더 채비가 필요합니다. 아직 당구대들이 우주 $M$위에서 변신하는 방법 $\Phi_t$를 구체적으로 모르기 때문일까요? 그도 그렇지만, 후술할 흐름 $\Phi_t$에 대해, 만약 $M$을 이전과 같이 단순히 당구대들의 집합으로 선택한다면 어떤 당구대도 회귀하지 못하는 일이 벌어지기 때문입니다. 결과적으로, $M$을 세상 모든 당구대들의 집합으로 선택하는 것은 조금은 순진한 시도였습니다. 이 문제는, 당구대 대신 `평행구조 곡면translation surface‘이라 불리는 그들의 아바타를 내세움으로써 자연스럽게 해결됩니다.
앞으로 우리는
1. 공간 $M$의 후보로 `아바타 당구대’들의 세계6와, 그 위의 흐름 $\Phi_t$를 정의할 것입니다.
2. 그리고 이 세계 속에서 회귀성을 보장해 줄 수 있는 두 가지 도구, 곧 메이저 기준Masur’s criterion 과 메이저-뷔치 측도Masur–Veech measure7를 소개하려 합니다.
5. 평행구조 곡면
앵무새의 속삭임을 잠시 멈추고, 우리는 곡면의 구조와 다각형 표현에 관한 이야기를 하려 합니다. 다각형을 풀칠하여 곡면을 얻는 내용은 최인혁 박사님의 만화 “이것은 기하학인가 아니면 위상수학인가 [2]: 자르고 붙이고 생각하고”를 읽어보시면 좋습니다. 여기에서는 간략히만 설명하려 합니다.
5.1 풀칠하기와 오려내기
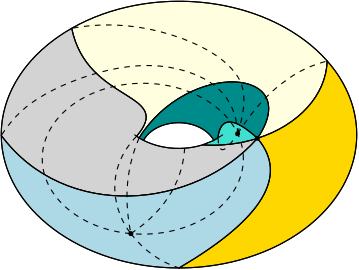
책상 위에 종이 한 장을 두고, 그 위에 다각형들을 그려봅시다. 그림 8 (a)의 다각형에는, 길이가 같고 방향이 나란한 변들이 두 쌍 (검정, 빨강) 있습니다. 이제 상상 속에서 그 쌍들을 하나하나 풀칠해 붙여 봅니다. 평면 위에 있던 도형이 어느새 접히고 이어져, 곡면이 탄생하게 됩니다. 이 곡면을 $S_1$이라 부르겠습니다.
주어진 다각형이 간단했던 덕분에, $S_1$이 도넛 모양의 곡면인 것을 어렵지 않게 상상할 수 있습니다. 더 복잡한 상황에 놓이더라도, 만약 아래의 `다각형 표현’이 주어진다면,
정의 5.1 `다각형 표현’이란, 다음을 말합니다.
1. 평면 위에 (여러 개의) 다각형들이 주어져 있고
2. 그 변들이 빠짐없이 한 쌍씩 같게 색칠 (또는 표시) 되어 있으며
3. 같게 색칠된 변들은 모두 길이가 같고 나란하며, 서로 반대 방향8
에 있을 것
우리는 상상 속에서 표시된 쌍들을 하나하나 풀칠할 수 있습니다.
즉, 다각형 표현이 주어지면 우리는 언제나 변들을 풀칠하여 곡면을 얻을 수 있으며, 거꾸로 곡면이 주어졌을 때 이것을 다각형으로 표현하려는 시도도 해 볼 수 있게 됩니다.
그림 8 (a)로 되돌아 가보겠습니다. 이번에는 아까와는 다르게 다각형을 풀칠하는 것 말고도 때로는 가위로 오려내 보기도 할 생각입니다. 대신 오려냈던 부분들은 꼭 기억하고 있다가, 나중에 잊지 말고 다시 풀칠해 주기로 합시다.
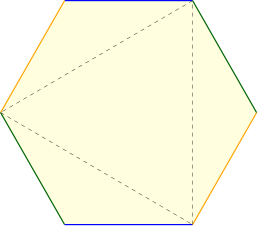
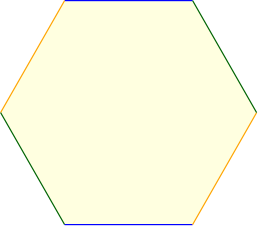
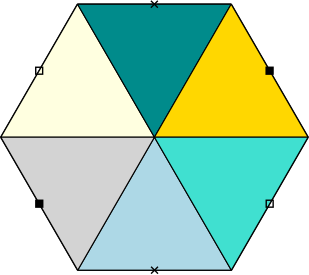
그림 8의 안내에 따라 (a), (b), (c), (d), (e), (f)의 순서대로 오려내고 풀칠하는 과정을 마치면 마지막 그림 8 (f)의 육각형 표현에 도달하게 됩니다. 그리고 이 육각형의 세 쌍의 마주보는 변들 (주황, 초록, 파랑) 을 마저 풀칠하면, 그림 9의 오른쪽에 보이는 것처럼 도넛 모양의 곡면을 얻게 됩니다.9 이 곡면을 $S_2$라고 부르겠습니다.
돌이켜보면 $S_1$에서 시작하여 그림 8의 안내 (a), (b), (c), (d), (e), (f)를 따르는 과정은, 곡면을 오려내거나, 전에 오려냈던 부위를 접합하는 행위의 연속이었습니다.
그런데 한번 오려냈던 부분들은 잊지 않고 나중에 언젠가는 다시 똑같은 위치에 붙이기로 약속했기에, 곡면 $S_2$는 어떤 의미에서는 $S_1$과 같은 곡면입니다.
그래서 우리는 그림 8 (a)의 평행사변형과 8 (f)의 육각형을, 겉모습은 다르지만 동일한 곡면을 나타내는 다각형 표현으로 여기려 합니다. 주어진 다각형 표현으로부터, 오려내기와 풀칠하기를 자유롭게 반복하며 얻어지는 모든 다각형 표현들의 무리를 동치류equivalence class 라고 부르겠습니다. 평행구조 곡면이란, 다각형 표현의 동치류로 정의됩니다.
평행구조 곡면의 풀칠하기 규칙은 평범한 곡면의 그것보다 훨씬 더 엄격합니다. 정의 5.1에 따르면, 단순히 다각형의 아무 변이나 붙일 수 있는 것이 아니라, 오직 평행이동으로 완벽히 포개지는 변들만이 짝을 맺을 수 있기 때문입니다. 이 제약으로 인해, 평행구조 곡면이 주어졌다는 것은, 곡면의 위상적 성질만이 아닌 더 많은 정보들이 주어졌다는 것을 의미합니다.
예를 들어, 그림 10의 다각형 표현을 통해 얻어지는 곡면을 $S_3$라 해 보겠습니다.
$S_3$는 도넛 모양의 곡면이 되는데, 이는 위상수학적으로는 그림 9의 다각형 표현에서 얻었던 곡면 $S_2$와 같은 곡면입니다. 하지만 $S_2$와 $S_3$는 평행구조 곡면으로서는 같지 않게 되는데, 이것은 그림 10의 다각형 표현으로부터는 어떤 오려내기와 풀칠하기 방법을 통해도 그림 9의 다각형 표현에 이르지 못한다는 것을 의미합니다.
평행구조 곡면에 주어지는 부가적인 정보가 무엇인지 정확히 알기 위해서는, 그것을 바라보는 다음의 서로 다른 시각들을 살펴보면 됩니다.
사실 5.2 평행구조 곡면은 다음 세 가지 서로 다른 방법으로 표현됩니다.
1. 다각형 표현들의 동치류가 주어지는 것
2. 리만 곡면과 그 위 정칙 미분형식holomorphic differential 이 주어지는 것
3. 위상 곡면 $\Sigma$와 그 위의 예외가 되는 점들 $P$, 그리고 이와 양립가능한 $\Sigma$의 평행지도10가 주어지는 것.
이 각각의 관점은 상황에 따라 자유롭게 오가며 활용할 수 있으며, 서로 다른 장점을 지닙니다.
예를 들어, 다각형 표현 두 개가 같은 평행구조 곡면을 나타내는지 판별하는 것은 결코 간단하지 않지만, 나머지 두 관점의 정의를 택했다면 이런 걱정에서는 자유롭게 됩니다.
우리는 첫 번째 관점, 즉 다각형 표현들의 언어를 중심으로 설명을 이어가겠습니다.
5.3 특이점과 지층
땅 위에 관찰자가 서 있습니다. 이 관찰자가 제자리에 서서 그의 주위를 둘러보며 시야각을 합산하는 것을 생각해 보겠습니다. 땅이 평면이라면, 관찰자가 어느 위치에 서 있을지라도, 그 결과는 늘 $360^\circ$, 호도법으로는 $2\pi$가 될 것입니다.
땅이 평면이 아닌 평행구조 곡면이었다면 결과는 조금 달라집니다. 평행구조 곡면에서는 대부분의 지면들은 평탄하지만 예외가 되는 뾰족한 점들이 몇 개 있습니다. 이 점들의 주변은 그림11과 같이 안장 모양의 지형을 이루게 됩니다. 그래서 정중앙에 있는 뾰족한 `안장점’에 도달한 관찰자는, 평소보다 넓은 시야를 얻어 합산한 시야각이 $2\pi$보다 크게 측정됩니다.
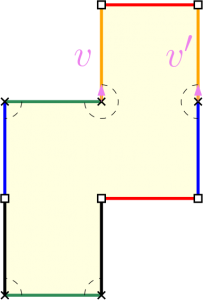
안장점들의 정식 명칭은 특이점singularity 입니다. 특이점을 자세히 정의하기 위해 그림 12의 왼쪽 Z자 다각형 표현에 대응되는 평행구조 곡면을 생각해 보겠습니다.
같은 색깔을 가진 변들이 풀칠된 곡면 위에서는 동일시된다는 것을 상기하면, 다음의 사실을 확인해 볼 수 있습니다.
연습 5.3 그림 12에서 $\times$로 표시된 모퉁이들은 모두 풀칠된 곡면에서 동일한 점을 나타냅니다.
마찬가지로, $\square$로 표시된 모퉁이들도 모두 풀칠된 곡면에서는 하나의 점이 됩니다.
이제 모퉁이 $\times$를 고정하고, 그것을 중심으로 하는 작은 원을 다각형 내부에 그려보겠습니다. 이 원을 따라 돌다 보면, 얻는 시야가 평소보다 더 넓은 $720^\circ$, 호도법으로는 $4\pi$임을 알아차리게 됩니다.
더 일반적으로, 임의의 평행구조 곡면과 그것의 한 다각형 표현을 생각해 보겠습니다.
다각형 표현의 모퉁이를 하나 선택하면, 같은 방법으로
다각형 내부에 모퉁이를 중심으로 하는 작은 원을 그리고,
그 원을 일정한 방향으로 따라 돌며 얻는 시야각을 합산
(5.1)
할 수 있습니다. 그려놓은 작은 원 위를 직접 도는 상상을 해 보겠습니다. 만약 원 위의 출발점이 변 $v$위에 놓여있었다면, 제자리로 돌아왔을 때 맞닥뜨리는 변 $v’$은 $v$와 색깔이 같은 변이어야 합니다. 한편 같은 색깔의 두 변은 평행해야 하기에, 합산된 각도는 언제나 $2\pi$의 정수배 $(2\pi, 4\pi, 6\pi, \cdots)$ 가 됨을 알 수 있습니다. 특이점이란 이 각도가 $2\pi$보다 큰 모퉁이들을 말합니다.
지금까지 평행구조 곡면에 나타날 수 있는 안장점들과, 그 안장점에 올랐을 때 관찰자가 얻는 시야각들에 대해 알아보았습니다. 이런 지질학적 정보들은 평행구조 곡면들을 세부적으로 분류하는 데 필요합니다. 평행구조 곡면들을 지질학적 정보에 따라 분류해 놓은 것을 지층stratum이라고 합니다.
더 구체적으로, 주어진 평행구조 곡면에 특이점, 즉 안장점들이 모두 $\ell$개 있다고 하고, 각각을 $p_1$, $\cdots$, $p_\ell$이라 해 보겠습니다. 이전 관찰에 의하면 각각의 안장점 $p_i$에 올랐을 때 얻는 시야각은 $2\pi$의 정수배입니다. 그러므로 그들은 어떤 자연수 $k_i$에 대해 $2\pi(k_i+1)$로 쓸 수 있게 됩니다. 이 정수 $k_i$ 들을 내림차순으로 다시 정렬하여 쓴 `지질학적 정보’ $(k_1,\cdots,k_\ell)$를 생각하겠습니다.
이제 지층이란, 같은 `지질학적 정보’11를 공유하는 평행구조 곡면들을 모두 모아놓은 공간을 말하며
$$
H(k_1,\cdots,k_\ell)
$$
로 표기합니다.
5.4 지층 조사하기
다각형 표현이 주어졌을 때, 그 평행구조 곡면의 종수나, 그것이 속하는 지층을 알아내려면 어떻게 해야 할까요? 이것을 구체적으로 알아보겠습니다. 다시 그림 12의 Z자 다각형 표현으로 얻는 평행구조 곡면을 생각해 보겠습니다. 다음 연습문제는 그림 12의 오른쪽 도형에서 직접 개수를 세어 답할 수 있습니다.
연습 5.4 그림 12의 Z자 다각형 표현에서, 풀칠이 끝난 뒤 남는 모퉁이, 변, 면의 수를 세어보면 각각 2, 5, 1개가 됩니다.
이제 종수가 $g$인 곡면의 오일러 특성값이 $2-2g$ 임을 상기하면 오일러 공식
$$
\text{(모서리의 개수)}-\text{(변의 개수)}+\text{(면의 개수)}=\text{(오일러 특성값)}
$$
으로부터 이 평행구조 곡면의 종수가 $g=2$임을 알 수 있습니다.
한편, 다각형 표현을 유심히 관찰하면, 우리는 각각의 안장점에서 얻는 시야각 (5.1) 도 눈으로 확인할 수 있습니다. 그림 12의 경우 특이점은 두 개 ($\times$와 $\square$) 이며, 두 특이점 모두 제자리를 돌면서 합산한 시야각이 $4\pi$가 됩니다. 즉 $\ell=2$, $k_1=k_2=1$이며 이 곡면이 속한 지층이 $H(1,1)$ 임을 알 수 있습니다.
이 논의를 일반적인 다각형 표현에 대해 반복하면, 더 일반적으로 곡면의 종수가 $g$이고 `지질학적 정보’가 $(k_1,\cdots,k_\ell)$ 로 주어진 평행구조 곡면에 대해서
$$
k_1+\cdots+k_\ell=2g-2
$$
의 관계가 성립하는 것을 알 수 있습니다. 그래서 평행구조 곡면의 지층은, 그 곡면이 가지고 있는 종수보다 더 세분화된 분류입니다. 한편, 이 관계는 위상 곡면의 종수가 주어졌을 때, 가능한 모든 지층의 종류도 알려줍니다. 예컨대 종수가 $g=3$인 곡면에서는
$$
4=3+1=2+2=2+1+1=1+1+1+1
$$
과 같은 분할이 가능하며, 따라서 가능한 지층은
$$
H(4),\,\,\, H(3,1),\,\,\, H(2,2),\,\,\, H(2,1,1),\,\,\, H(1,1,1,1)
$$
모두 이렇게 5종류가 됩니다.
5.5 2×2 행렬군 $\mathrm{SL}(2,\mathbb{R})$ 의 작용
우리는 당구의 문제에서 출발했지만, 어느새 평행구조 곡면이라는 무대 위로 올라와 있습니다. 자연스럽게, 우리의 관심도 평행구조 곡면 위의 동역학으로 옮겨가려 합니다.
평행구조 곡면들의 세계에는 면적을 보존하는 2×2 행렬군, 곧 $\mathrm{SL}(2,\mathbb{R})$의 자연스러운 작용이 깔려 있습니다. 임의의 행렬 $A \in \mathrm{SL}(2,\mathbb{R})$를 집어 들고, 한 평행구조 곡면 $X$의 다각형 표현을 떠올려 봅시다. 각 변 $v_i$를 단순한 선분이 아니라 평면 벡터로 바라보면, 행렬 곱 $Av_i$는 또 하나의 벡터를 낳습니다. 이제 $X$의 원래 있던 다각형 표현에서, 변의 색깔은 그대로 두면서 각 변 $v_i$를 새로운 벡터 $A.v_i$로 교체하겠습니다. 이 결과로 우리는 정의 5.1를 만족하는 새로운 다각형 표현을 얻게 되는데 이것이 가리키는 평행구조 곡면을 바로 $A.X$로 정의하게 됩니다.
구체적으로, 다음과 같은 대각 행렬을 생각해 보겠습니다:
\begin{equation}\label{eq.at}
a_t=
\begin{bmatrix}
e^t&0\\
0&e^{-t}
\end{bmatrix}
\end{equation}
(5.2)
이 행렬을 벡터 $v = \begin{bmatrix} x\\y\end{bmatrix}$ 에 적용하면
$$
a_t.v=
\begin{bmatrix}
e^t&0\\
0&e^{-t}
\end{bmatrix}
\begin{bmatrix}
x\\
y
\end{bmatrix}
=
\begin{bmatrix}
e^tx\\
e^{-t}y
\end{bmatrix}
$$
라는 결과를 얻게 됩니다. 곧 가로 방향은 $e^t$배 늘어나고, 세로 방향은 $e^{-t}$배 줄어든 벡터이지요. 이 변형을 따라 다각형의 변들이 찌그러지고 늘어난 모습이 바로 새로운 평행곡면 $a_t.X$의 다각형 표현입니다.
이러한 변형에도 불구하고, 행렬의 작용은 곡면의 몇가지 본질을 바꾸지 않습니다.
종수가 2인 곡면에 아무리 $\mathrm{SL}(2,\mathbb{R})$의 요소들을 적용해도, 그 배경이 되는 위상곡면은 여전히 종수 2로 남습니다. 뿐만 아니라, 곡면이 속한 지층 또한 변하지 않습니다.
그래서 특정 평행구조 곡면 $X$의 흐름을 추적할 때는, 모든 종수 $g$의 곡면들을 한꺼번에 보는 대신, $X$가 속한 바로 그 지층 속에서 이야기를 전개하는 것이 훨씬 더 합리적인 선택이 됩니다. 이것은 평행구조 곡면과 동역학 이야기를 할 때 지층 이야기가 빠질 수 없는 이유입니다.
6. 앵무새가 다시 등장하다
이제 앵무새가 돌아옵니다. 그 녀석은 지금 L자 당구대 위의 숨겨진 비밀12을 알아내려 애쓰고 있습니다. 대체 어떤 방법을 쓰려는 걸까요? 매우 제멋대로인 녀석이기에, 자기 신념대로 당구대를 “북쪽”을 향해 묻지도 따지지도 않고 힘껏 날려버립니다.
먼저, L자 당구대를 그림13의 맨 왼쪽에서처럼 정방향으로 배치하고, 북쪽 방향으로 타격하는 상황을 상상해 보겠습니다. 앵무새가 알려주지 않은 비밀 규칙이 있는데요, 그의 말에 따르면 L자 당구대는 이 규칙에 따라 그림13의 오른쪽 모습들로 서서히 변신을 시작합니다.
“시간 $t$가 지나면 세로 길이는 $e^t$배 늘어나고, 가로 길이는 $e^{-t}$배 줄어들어.
당구대는 점점 가늘어지고 길쭉해지지만, 면적만큼은 절대 변하지 않아.”
(6.1)
물론 앵무새는 타격 방향을 바꿔서 당구대를 칠 수도 있습니다. 설명의 편의를 위해, 그림 14의 맨 왼쪽에서와 같이 타격 방향은 그대로 북쪽이지만, L자 당구대를 살짝 기울여 배치하는 상황으로 대체하겠습니다. 이제 당구대는 시간이 지남에 따라 그림14의 오른쪽 모습들로 변신합니다.
이제 당구대가 어떻게 움직이는지는 잘 알 것 같습니다. 하지만 당구대는 끊임없이 찌그러지기만 할 뿐, 다시 원래의 모습으로 돌아올 기미는 보이지 않습니다. 아무리 방향을 바꿔서 타격해도 상황은 마찬가지입니다.
6.1 아바타 당구대
다행히 앵무새가 진정 염두에 두었던 당구대는 애초에 L자 당구대가 아니었으며, 그에게는 $L$자 당구대의 아바타 역할을 수행할 또 다른 당구대가 준비되어 있습니다.
그것은 바로 L자 당구대 네 개를 이어 붙여 만든, 그림 15와 같은 십자 모양의 당구대입니다.
이 십자 당구대는 단순히 $L$자 당구대 네 조각을 붙여 만든 도형 같지만, 특별한 규칙이 덧붙습니다. 마주 보는 같은 색의 벽들을 모두 `같은 것’으로 간주하는 것입니다.
이 규칙이 적용되면, 벽은 사실상 없는 것과 마찬가지입니다. 공은 더 이상 벽에 부딪혀 튕겨 나오지 않고, 대신 그대로 순간이동되어 맞은편의 같은 색을 가진 벽 위치에서 튀어나옵니다. 이 `벽이 사라진 당구대’라는 새로운 대상은 우리가 이미 정의했던 평행구조 곡면의 특별한 예입니다.
방금 우리는 L자 당구대로부터 시작하여, 당구대를 복사하고 벽을 지워내는 (풀칠하는) 방법으로 평행구조 곡면을 만들어냈습니다. 이 방식은 사실 모든 유리각 당구대에 적용될 수 있습니다. 그 핵심은 반사군reflection group에 있습니다.
평면 위의 반사 변환은 어떤 2×2 행렬 $A$와 벡터 $b$를 써서 $x \mapsto Ax+b$라 표현할 수 있습니다. 이제 유리각 당구대가 주어지면, 각 변마다 대응되는 행렬을 얻을 수 있고, 벽 사이의 각도가 유리수라는 사실 때문에 이 행렬들은 결국 유한군을 이루게 됩니다. 이를 우리는 반사군이라 부릅니다. 예컨대 L자 당구대의 경우, 이 반사군은 단출하게도 $\mathbb{Z}_2 \times \mathbb{Z}_2$입니다.
이제 반사군의 각 원소마다 당구대를 반사시켜 얻은 복사본을 하나씩 준비해 봅시다. 만약 반사군의 원소가 $m$개라면, $m$개의 당구대가 생겨납니다. 그 다음 단계는 이미 익숙하지요. 벽을 없애고, 없앤 자리를 순간이동 장치로 대체하면, 평행구조 곡면을 얻게 됩니다.
6.2 직선흐름
십자 당구대를 $L$자 당구대의 아바타 당구대라고 부른 까닭이 있습니다. 그것은 십자 당구대 위의 공의 궤적이 곧 $L$자 당구대 위 공의 궤적와 밀접하게 맞닿아 있기 때문입니다.
그림 16의 두 당구대를 나란히 보며 설명을 마무리하겠습니다. 왼쪽 그림의 점선은 L자 당구대 위에서 공이 당구흐름을 따라 움직이는 모습입니다. 그리고 오른쪽 그림의 점선은 십자 당구대에서 이에 대응되는, 같은 지점에서 같은 방향으로 출발시킨 공의 궤적입니다. 왼쪽 당구흐름에서 공이 벽과 부딪혀 반사가 일어나는 순간마다, 오른쪽 궤적의 공은 (반사군의 원소에 대응되는) 다른 사본 당구대로 순간이동하여 직선운동을 계속합니다. 아바타 당구대 위의 직선운동하는 공의 궤적을 우리는 직선흐름Straight line flow이라고도 부릅니다.
직선흐름은 더 일반적으로, 모든 평행구조 곡면에서 정의됩니다. 평행구조 곡면에서는 특이점들을 제외한 모든 곳에서 잘 정의된 `북쪽’이 존재합니다. 안장점이 아닌 곳 어디에서나 나침반을 꺼내 들면, 어디로 가야 할지 방향을 알 수 있는 셈이지요. 직선흐름이란, 이렇게 평행구조 곡면 위에서 고정된 방향으로 직선운동을 계속하는 흐름을 말합니다.
이렇게 해서, 우리는 구불구불 접혀있는 유리각 당구대 위 공의 흐름을 펼쳐내면, 평행구조 곡면 위의 직선흐름이 된다라는 사실에 눈을 뜨게 됩니다.
6.3 앵무새가 꿈꾸던 공간
따라서 앵무새가 진정으로 마음속에 품고 있던 `당구대들의 공간’ $M$은 결국 평행구조 곡면들의 집합이었습니다.
아바타 당구대를 치는 법 $\Phi_t: M\to M$은 어떻게 되는 걸까요? 방법은 이전 규칙(6.1)과 유사합니다. 아바타 당구대를 $X$라 할 때, $X$의 다각형 표현을 규칙 (6.1) 에 따라 변신시키는 것입니다. 그리고 이 과정은 (5.2)에서 언급한 $2\times2$ 행렬 $a_t$가 $X$에 작용한 것으로도 이해할 수 있습니다.
$$
\textit{아바타 당구대 $X$를 북쪽을 향해 타격하면, $t$초 후 $\Phi_t(X)=a_t.X$로 변신합니다.}
$$
지금까지 우리는 당구대들의 우주 $M$과 그 안의 흐름 $\Phi_t: M\to M$에 대해 알아보았습니다. 그러나 여기에는 아직 풀리지 않은 숙제가 남아 있습니다. 이 평행구조 곡면들의 집합 $M$ 위의 흐름이 언제, 어떻게 회귀성을 갖는지, 그 기준을 밝혀내야 한다는 점입니다.
다음 화의 시작은 이 회귀성을 담보해 줄 수 있는 도구인 메이저-뷔치 측도Masur-Veech measure), 그리고
정리 6.1 [메이저 기준 (Masur’s Criterion)]13 평행구조 곡면 $X$에 대하여 다음 두 사실은 서로 동치입니다.
1. 흐름 $a_t.X$가 $X$가 속한 지층에서 회귀성을 갖는다.
2. 거의 모든 각도 $\theta$에 대해, $X$의 $\theta$ 방향 직선흐름이 유일 에르고딕성을 갖는다.
의 설명과 함께할 예정입니다.
7. 맺는 글
이 글 속 앵무새는 허구이지만, 그가 상징하는 정신은 실재합니다. “매개변수 공간에 작물을 심고, 위상 공간에서 수확하라14”는 말과 함께, 수학자들 사이에 세대와 세대를 거쳐 이어지는 정신이지요.
재규격화는 결코 당구 문제에만 국한되지 않습니다.
직접적으로 언급되지 않을 뿐, 동역학 전반에 걸쳐 곳곳에서 스며나옵니다. 이번 글에서는 당구대를 핑계 삼아 재규격화 이야기를 펼쳤지만, 동시에 그 틈을 타 매개공간과 평행구조 곡면의 세계로 한 발 들어오는 길도 마련했습니다.
7.1 끝맺음의 시
Not all who wander are but rolling balls,
떠도는 것이 다 공일 수 없으며,
Nor all tables of billiards forever at rest.
당구대라고 하여 영원히 고요한 것도 아니다.
참고문헌
- [La] V.F. Lazutkin, \textit{Existence of caustics for the billiard problem in a convex domain.} Izv. Akad. Nauk SSSR Ser. Mat. 37 (1973), 186-216.
- [KMS] S. Kerckhoff, H. Masur, J. Smillie, \textit{Ergodicity of billiard flows and quadratic differentials.} Ann. of Math. (2) 124 (1986), no. 2, 293-311.
- [Mas1] H. Masur, \textit{Interval exchange transformations and measured foliations.} Ann. of Math. (2) 115 (1982), no. 1, 169-200.
- [Mas2] H. Masur, \textit{Hausdorff dimension of the set of nonergodic foliations of a quadratic differential.} Duke Math. J. 66 (1992), no. 3, 387-442.
- [Vee] W. A. Veech, \textit{Gauss measures for transformations on the space of interval exchange maps.} Ann. of Math. (2) 115 (1982), no. 1, 201-242.